Research on Radar Waveform Design Strategy under Game Condition
-
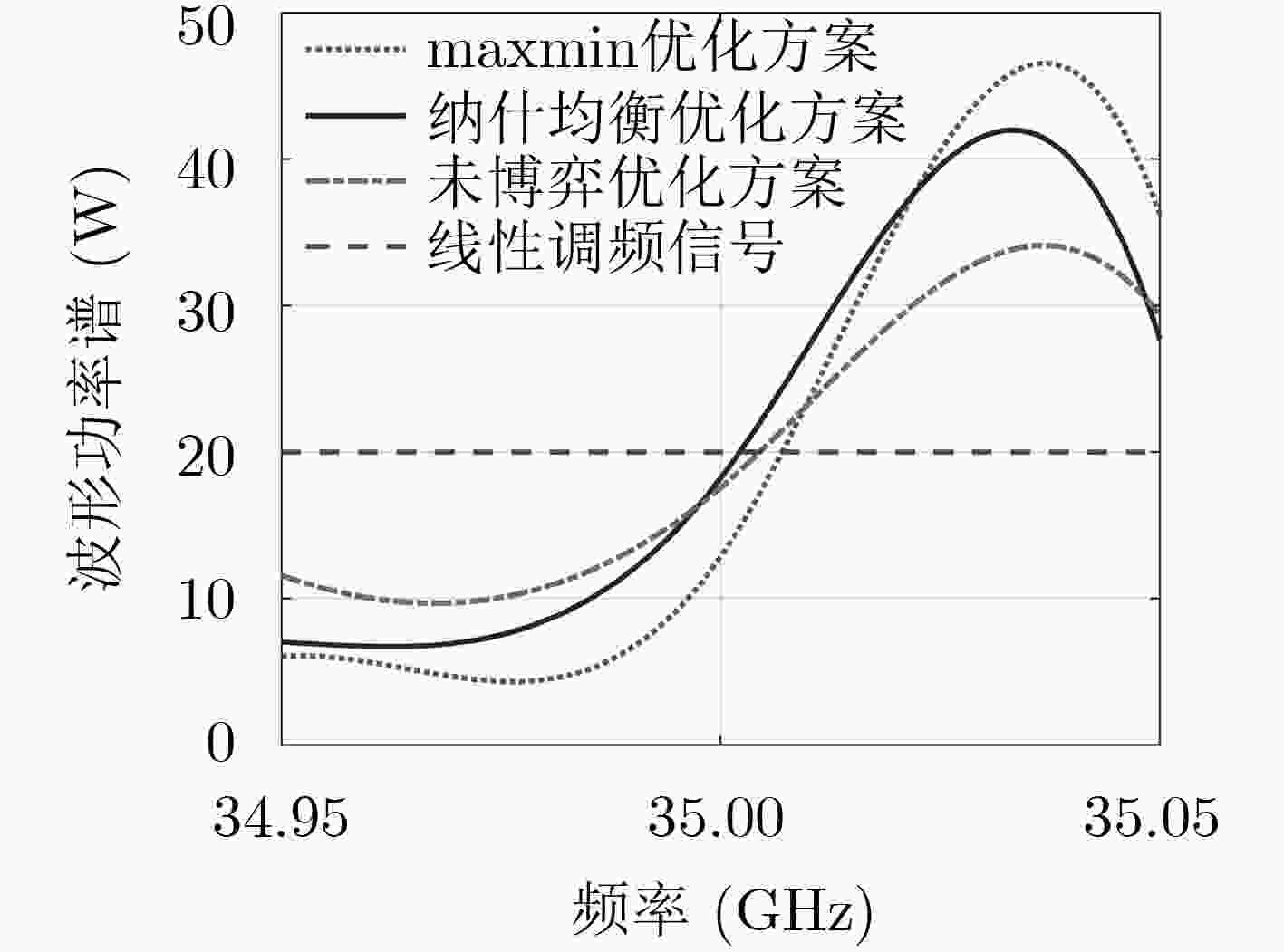
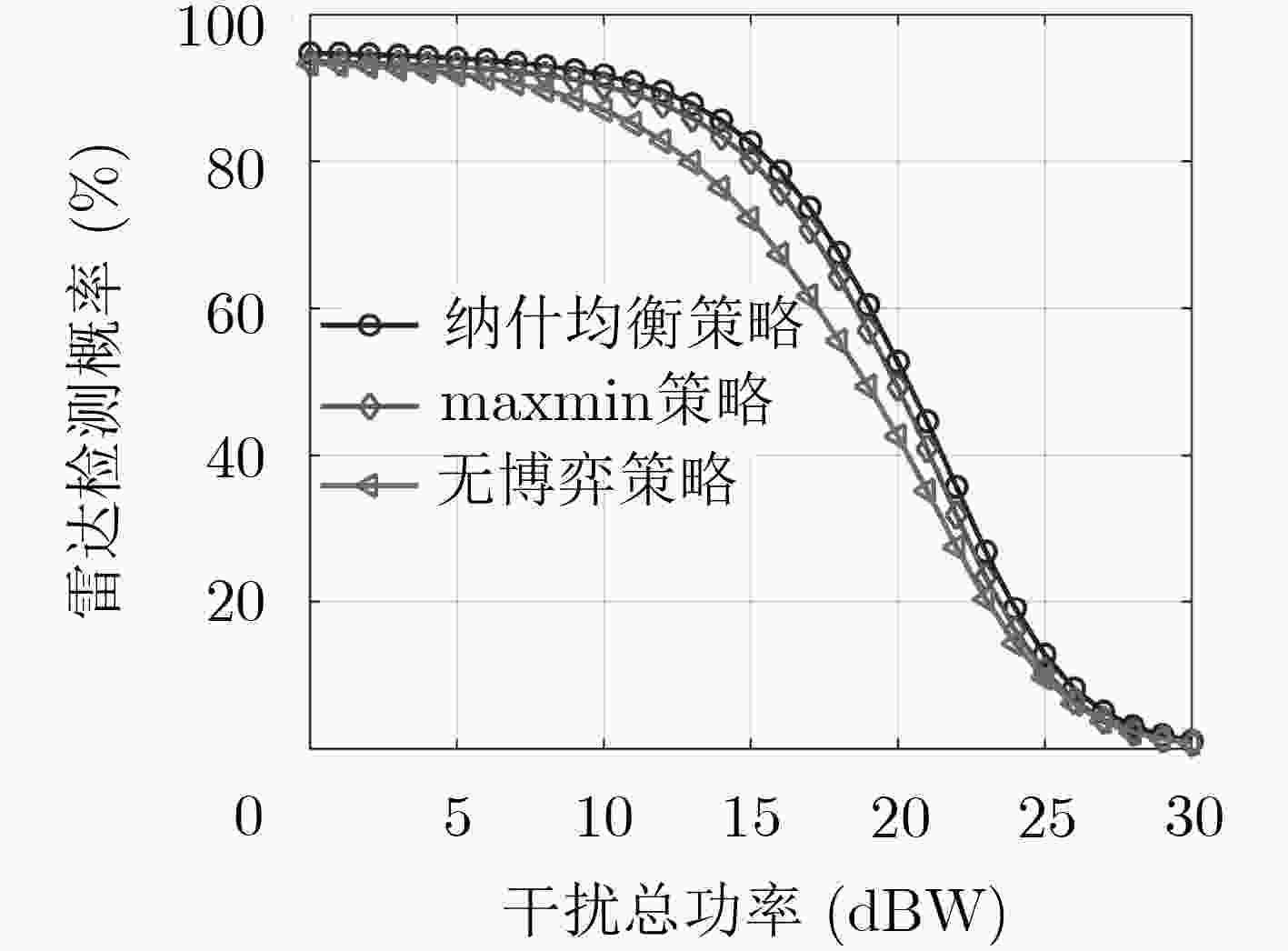
摘要: 为提高电子战中弹载雷达检测性能,该文提出基于纳什均衡的雷达波形设计方法。首先建立电子战条件下雷达与干扰信号博弈模型,基于最大化信干噪比(SINR)准则,分别设计了雷达和干扰的波形策略;然后通过数学推导论证了博弈纳什均衡解的存在性,设计了一种重复剔除严格劣势的多次迭代注水方法来实现纳什均衡;通过二步注水法推导了非均衡的maxmin优化方案;最后通过仿真实验测试不同策略下雷达检测性能。仿真结果证明,基于纳什均衡的雷达信号设计有助于提升博弈条件下雷达检测性能,对比未博弈时,雷达检测概率最高可提升12.02%,较maxmin策略最高可提升3.82%,证明所设计的纳什均衡策略更接近帕累托最优。Abstract: In order to improve missile-borne radar detection performance in modern electronic warfare, a radar waveform design method based on Nash equilibrium is proposed. Firstly, the radar and jammer game signal models are established in electronic warfare. Based on maximum Signal-to-Interference-plus-Noise Ratio (SINR), waveform strategies of radar and jammer are designed respectively. Secondly, the existence of Nash equilibrium solution is demonstrated by mathematical derivation and verified in experimental simulation. A multiple iterative water-filling method which repeatedly eliminates strict disadvantages is designed to achieve Nash equilibrium. The maxmin scheme of disequilibrium game is deduced by two-step water-filling method. Finally, the radar detection performance of optimization strategies is tested by simulation experiments. Simulation results reveal that the radar waveform design based on Nash equilibrium is beneficial to improve the radar detection performance under game conditions. Compared with no-game and maxmin strategies, the radar detection probability of Nash equilibrium strategy can be increased by 12.02% and 3.82%, respectively. It is proved that the Nash equilibrium strategy of this paper is closer to the Pareto optimality.
-
表 1 迭代注水算法
(1) 初始化双方策略) $\left| {S({f_k})} \right| = {\left| {S({f_k})} \right|_0}$, $J({f_k}) = J{({f_k})_0}$ (2) 最大化雷达效益$\mathop {\max }\limits_{{\rm{SINR}}} \left( {{{\left| {S({f_k})} \right|}^*},\lambda } \right)$ (3) 更新雷达策略$\left| {S({f_k})} \right| = {\left| {S({f_k})} \right|^ * }$ (4) 最大化干扰效益$\mathop {\min }\limits_{{\rm{SINR}}} \left( {J{{({f_k})}^*},\gamma } \right)$ (5) 更新干扰策略$J({f_k}) = J{({f_k})^ * }$ (6) 重复步骤(2)—步骤(5)直到${\left| {S({f_k})} \right|^ * }$与$J{({f_k})^ * }$保持不变 表 2 各频带功率分配策略及性能
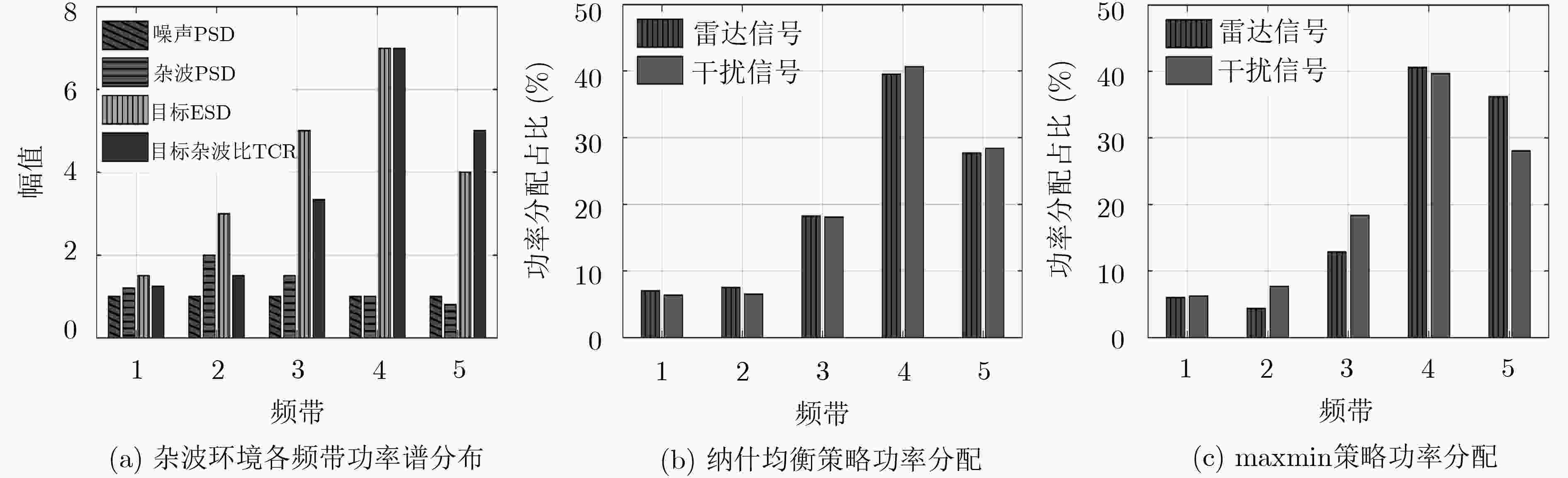
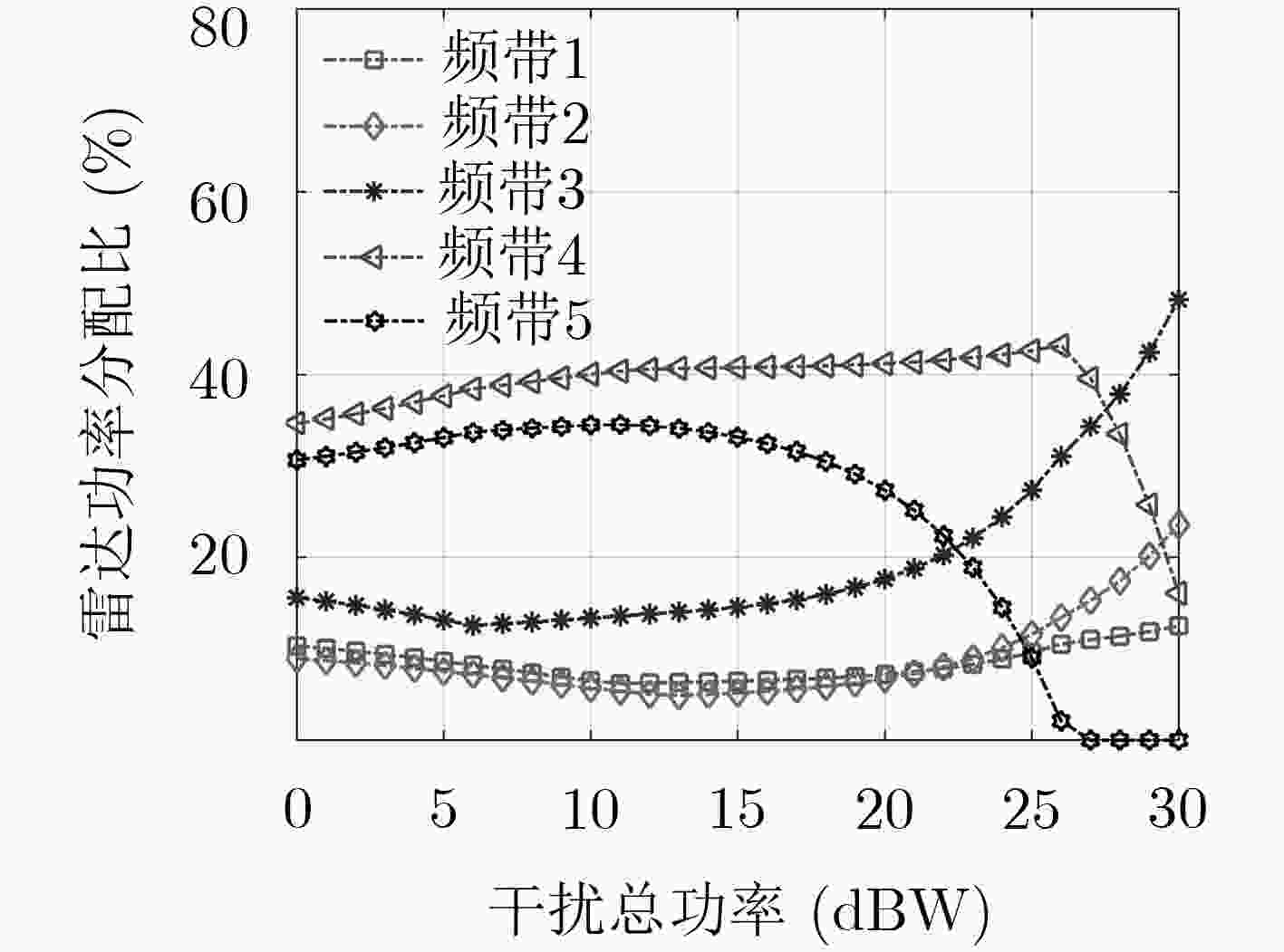
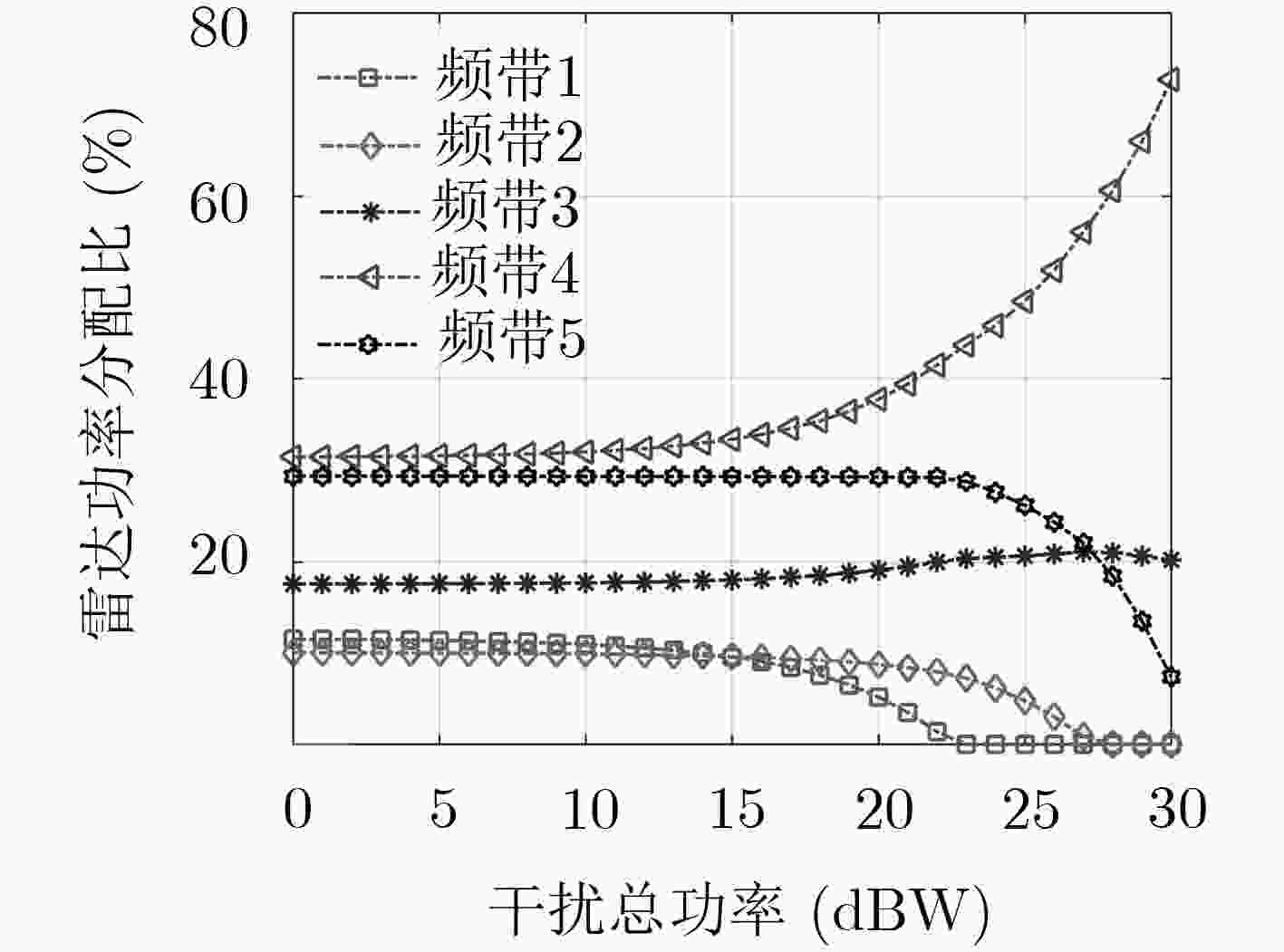
策略 子带1(W) 子带2(W) 子带3(W) 子带4(W) 子带5(W) SINR(dB) 检测概率(%) 运算时间(s) 纳什均衡 雷达 7.0313 7.5312 18.2321 39.5216 27.6882 9.761 52.72 1.537 干扰 6.3916 6.5261 18.0624 40.6172 28.4126 maxmin 雷达 6.0337 4.3443 12.8720 40.5470 36.2027 9.554 49.31 0.485 干扰 6.2589 7.7107 18.3573 39.6503 28.0359 -
HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30–40. doi: 10.1109/MSP.2006.1593335 翁木云, 郑家毅, 李伟, 等. 低RCS目标检测的制导雷达波形优化方法[J]. 华中科技大学学报: 自然科学版, 2019, 47(2): 41–46. doi: 10.13245/j.hust.190208WENG Muyun, ZHENG Jiayi, LI Wei, et al. Guidance radar waveform optimization method for low RCS target detection under interference conditions[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2019, 47(2): 41–46. doi: 10.13245/j.hust.190208 BELL M R. Information theory and radar waveform design[J]. IEEE Transactions on Information Theory, 1993, 39(5): 1578–1597. doi: 10.1109/18.259642 PILLAI S U, OH H S, YOULA D C, et al. Optimal transmit-receiver design in the presence of signal-dependent interference and channel noise[J]. IEEE Transactions on Information Theory, 2000, 46(2): 577–584. doi: 10.1109/18.825822 KAY S. Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter/reverberation[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(1): 31–41. doi: 10.1109/jstsp.2007.897046 ROMERO R A, BAE J, and GOODMAN N A. Theory and application of SNR and mutual information matched illumination waveforms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 912–927. doi: 10.1109/TAES.2011.5751234 AUBRY A, DEMAIO A, FARINA A, et al. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 93–117. doi: 10.1109/TAES.2013.6404093 WU Linlong, BABU P, and PALOMAR D P. Transmit waveform/receive filter design for MIMO radar with multiple waveform constraints[J]. IEEE Transactions on Signal Processing, 2018, 66(6): 1526–1540. doi: 10.1109/TSP.2017.2787115 IMANI S, NAYEBI M M, and GHORASHI S A. Colocated MIMO radar SINR maximization under ISL and PSL constraints[J]. IEEE Signal Processing Letters, 2018, 25(3): 422–426. doi: 10.1109/LSP.2018.2796603 BUTT F A, NAQVI I H, and RIAZ U. Hybrid phased-MIMO radar: A novel approach with optimal performance under electronic countermeasures[J]. IEEE Communications Letters, 2018, 22(6): 1184–1187. doi: 10.1109/LCOMM.2018.2828408 WANG Li, WU Huaqing, and STÜBER G L. Cooperative jamming-aided secrecy enhancement in P2P communications with social interaction constraints[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 1144–1158. doi: 10.1109/TVT.2016.2553121 GUAN Yanpeng and GE Xiaohua. Distributed secure estimation over wireless sensor networks against random multichannel jamming attacks[J]. IEEE Access, 2017, 5: 10858–10870. doi: 10.1109/ACCESS.2017.2713807 WANG Lulu, WANG Hongqiang, WONG K K, et al. Minimax robust jamming techniques based on signal-to-interference-plus-noise ratio and mutual information criteria[J]. IET Communications, 2014, 8(10): 1859–1867. doi: 10.1049/iet-com.2013.1054 FENG Dejun, XU Letao, PAN Xiaoyi, et al. Jamming wideband radar using interrupted-sampling repeater[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1341–1354. doi: 10.1109/TAES.2017.2670958 SONG Xiufeng, WILLETT P, ZHOU Shengli, et al. The MIMO radar and jammer games[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 687–699. doi: 10.1109/TSP.2011.2169251 GAO Hao, WANG Jian, JIANG Chunxiao, et al. Equilibrium between a statistical MIMO radar and a jammer[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 461–466. doi: 10.1109/RADAR.2015.7131043. LAN Xing, LI Wei, WANG Xingliang, et al. MIMO radar and target stackelberg game in the presence of clutter[J]. IEEE Sensors Journal, 2015, 15(12): 6912–6920. doi: 10.1109/JSEN.2015.2466812 KAY S M and LUO Pengfei. Fundamentals of Statistical Signal Processing: Estimation and Detection Theory[M]. Beijing: Publishing House of Electronics Industry, 2014: 425–445. 邹鲲. 认知雷达的未知目标检测[J]. 电子与信息学报, 2018, 40(1): 166–172. doi: 10.11999/JEIT170254ZOU Kun. Unknown target detection for cognitive radar[J]. Journal of Electronics &Information Technology, 2018, 40(1): 166–172. doi: 10.11999/JEIT170254 CARABALLO M A, MÁRMOL A M, MONROY L, et al. Cournot competition under uncertainty: Conservative and optimistic equilibria[J]. Review of Economic Design, 2015, 19(2): 145–165. doi: 10.1007/s10058-015-0171-z FUDENBERG D and TIROLE J. Game Theory[M]. Cambridge: MIT Press, 1991: 18–26. -





 下载:
下载:


 下载:
下载:
