Research of Low Sampling Frequency Broadband Digital Predistortion with Cyclostationary Characteristics
-
摘要:
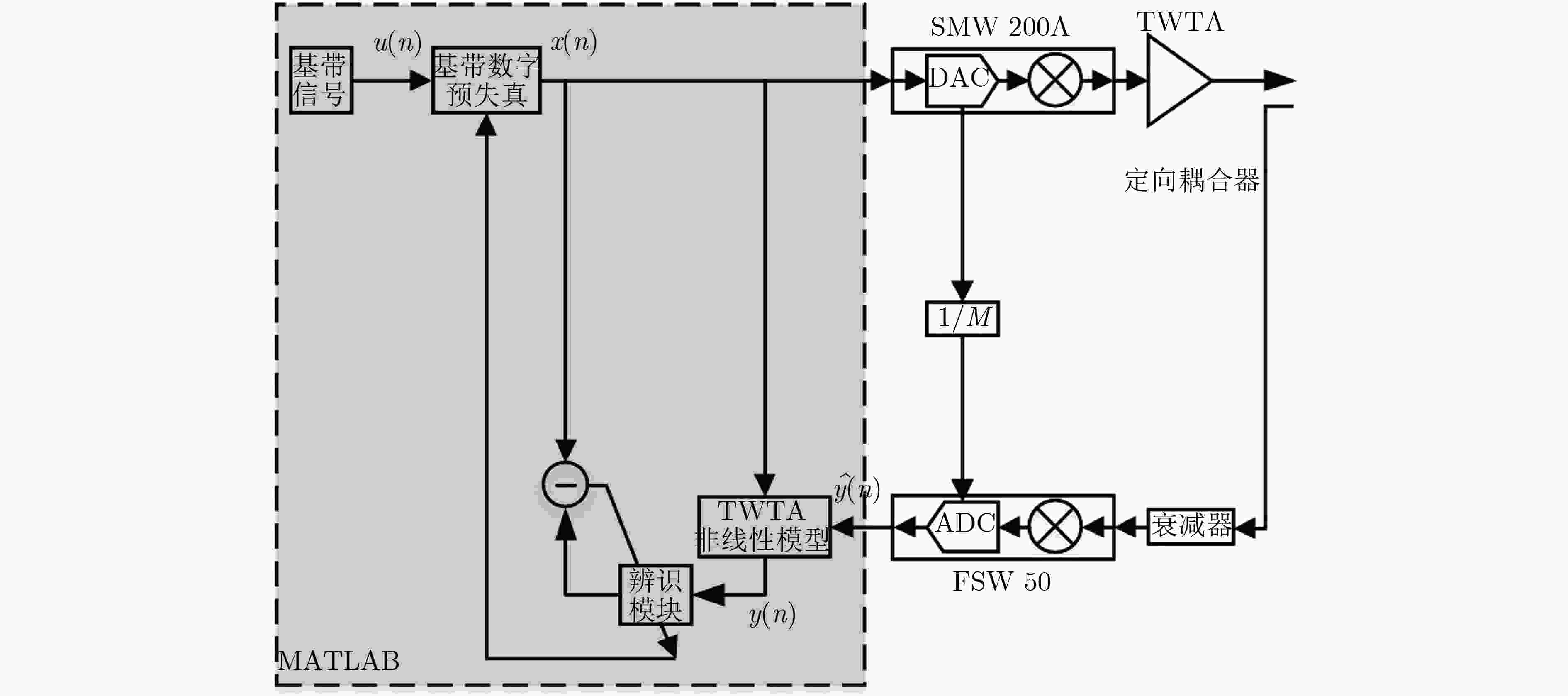
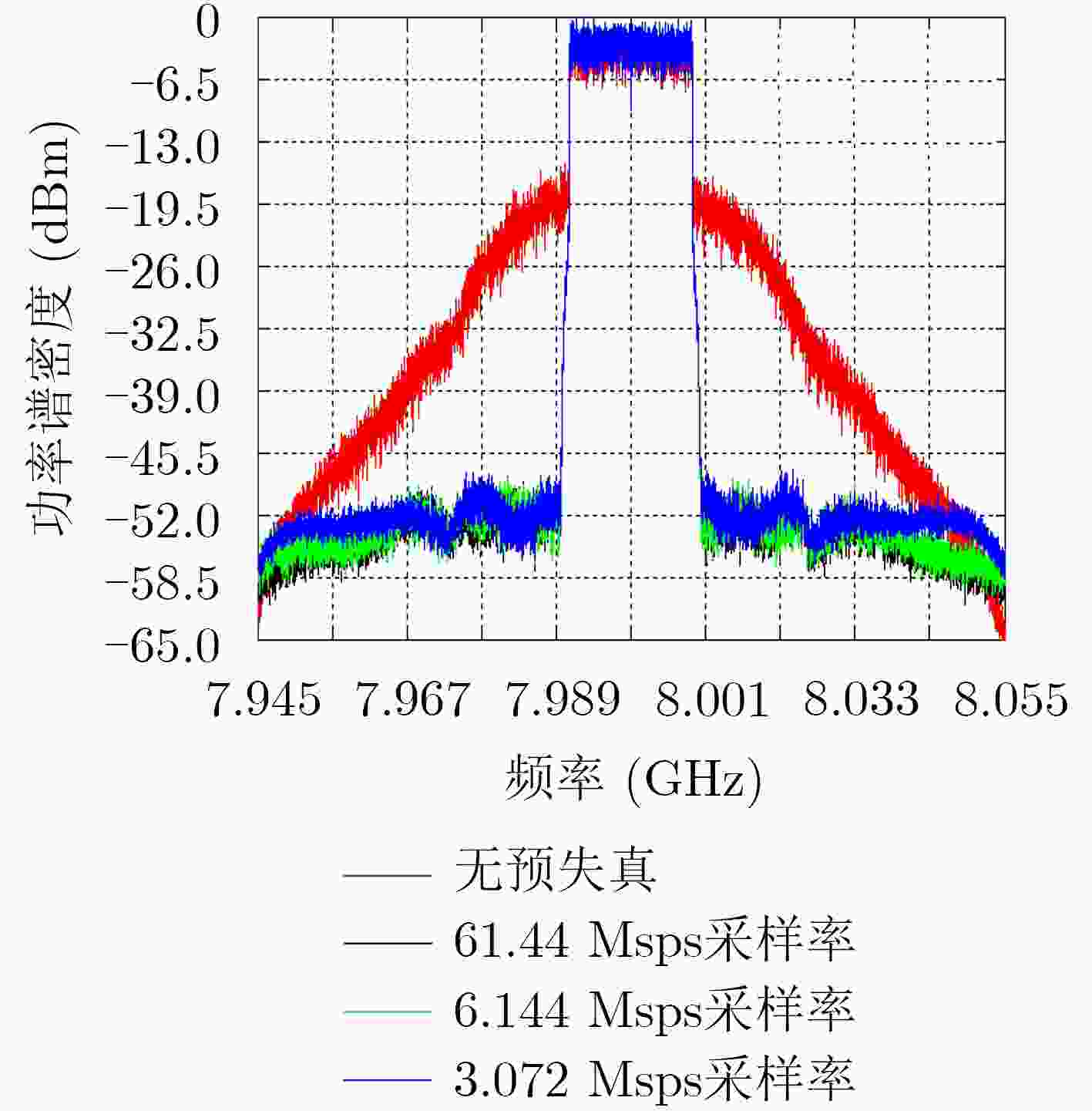
为了解决行波管(TWT)宽带数字预失真(DPD)中反馈回路ADC采样率过高的问题,该文利用信号的循环平稳特性证实可通过欠采样下的输出信号估计功放的非线性模型参数,然后由功放非线性模型参数和输入信号可恢复出与高采样率下效果相似的功放输出信号,最后通过传统的间接学习结构对功放进行数字预失真以实现行波管的线性化。为了验证该方法,利用20 MHz LTE信号驱动一只55 W的X波段行波管放大器(TWTA)。数字预失真反馈回路的ADC采样率从61.44 Msps降低至6.144 Msps和3.072 Msps,但线性化效果变化不大,表明欠采样方法是有效的。
Abstract:In order to reduce the sampling rate of the Traveling Wave Tube (TWT) of the Analog to Digital Converter (ADC) in the feedback loop of Digital PreDistortion (DPD), the nonlinear parameters of the power amplifier model are proved to be estimated with the undersampled output signal based on the cyclostationary of digital modulation signal. The output signal similar to high sampling rate can be obtained by combining the nonlinear parameters of the power amplifier model with the input signal. The DPD of the power amplifier is implemented through indirect learning architecture. To validate the method, a 55 W X-band Traveling Wave Tube Amplifier (TWTA) is driven by a 20 MHz LTE signal. The sampling rate of ADC in the DPD feedback loop is reduced from 61.44 Msps to 6.144 Msps and 3.072 Msps, but the linearization effect has little change, which shows the validation of the undersampling method.
-
表 1 不同采样率下预失真的邻近信道功率比
预失真采样率(Msps) ACPR-/+20 MHz(dBc) ACPR-/+40 MHz(dBc) 无预失真 –19.24/–19.94 –37.84/–39.34 61.44 –47.42/–47.78 –49.30/49.00 6.144 –47.07/–47.55 –48.72/–48.15 3.072 –46.87/–46.40 –48.06/–48.40 -
DUNN Z, YEARY M, FULTON C, et al. Wideband digital predistortion of solid-state radar amplifiers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(5): 2452–2466. doi: 10.1109/TAES.2016.150142 WOOD J. System-level design considerations for Digital Pre-Distortion of wireless base station transmitters[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(5): 1880–1890. doi: 10.1109/TMTT.2017.2659738 YU Chao, GUAN Lei, ZHU Erni, et al. Band-limited Volterra series-based digital predistortion for wideband RF power amplifiers[J]. IEEE Transactions on Microwave Theory and Techniques, 2012, 60(12): 4198–4208. doi: 10.1109/TMTT.2012.2222658 LIU Youjiang, YAN J J, DABAG H T, et al. Novel technique for wideband digital predistortion of power amplifiers with an under-sampling ADC[J]. IEEE Transactions on Microwave Theory and Techniques, 2014, 62(11): 2604–2617. doi: 10.1109/TMTT.2014.2360398 MA Yuelin, YAMAO Y, AKAIWA Y, et al. Wideband digital predistortion using spectral extrapolation of band-limited feedback signal[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2014, 61(7): 2088–2097. doi: 10.1109/TCSI.2013.2295897 LIU Ying, PAN Wensheng, SHAO Shihai, et al. A general digital predistortion architecture using constrained feedback bandwidth for wideband power amplifiers[J]. IEEE Transactions on Microwave Theory and Techniques, 2015, 63(5): 1544–1555. doi: 10.1109/TMTT.2015.2416184 ZHANG Qi, LIU Youjiang, ZHOU Jie, et al. A band-divided memory polynomial for wideband digital predistortion with limited bandwidth feedback[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2015, 62(10): 922–926. doi: 10.1109/TCSII.2015.2457793 WANG Zonghao, CHEN Wenhua, SU Gongzhe, et al. Low feedback sampling rate digital predistortion for wideband wireless transmitters[J]. IEEE Transactions on Microwave Theory and Techniques, 2016, 64(11): 3528–3539. doi: 10.1109/TMTT.2016.2602216 GUAN Ning, WU Nan, and WANG Hua. Digital predistortion of wideband power amplifier with single undersampling ADC[J]. IEEE Microwave and Wireless Components Letters, 2017, 27(11): 1016–1018. doi: 10.1109/LMWC.2017.2750059 LIU Ying, PAN Wensheng, SHAO Shihai, et al. A new digital predistortion using indirect learning with constrained feedback bandwidth for wideband power amplifiers[C]. 2014 IEEE MTT-S International Microwave Symposium, Tampa, USA, 2014: 1-3. doi: 10.1109/MWSYM.2014.6848259. GARDNER W A. Introduction to Random Processes: With Applications to Signals and Systems[M]. 2nd ed. New York, USA: McGraw-Hill, 1990: 302–310. REED I. On a moment theorem for complex Gaussian processes[J]. IRE Transactions on Information Theory, 1962, 8(3): 194–195. doi: 10.1109/TIT.1962.1057719 ZHOU G T and KENNEY J S. Predicting spectral regrowth of nonlinear power amplifiers[J]. IEEE Transactions on Communications, 2002, 50(5): 718–722. doi: 10.1109/TCOMM.2002.1006553 BRILLINGER D R. Time Series: Data Analysis and Theory[M]. San Francisco, USA: Holden Day, 1981: 19-27. GARDNER W A. Spectral correlation of modulated signals: Part I - analog modulation[J]. IEEE Transactions on Communications, 1987, 35(6): 584–594. doi: 10.1109/TCOM.1987.1096820 GARDNER W A, BROWN III W A, and CHEN C K. Spectral correlation of modulated signals: Part II - digital modulation[J]. IEEE Transactions on Communications, 1987, 35(6): 595–601. doi: 10.1109/TCOM.1987.1096816 -





 下载:
下载:


 下载:
下载:
