Deep Convolution Blind Separation of Acoustic Signals Based on Joint Diagonalization
-
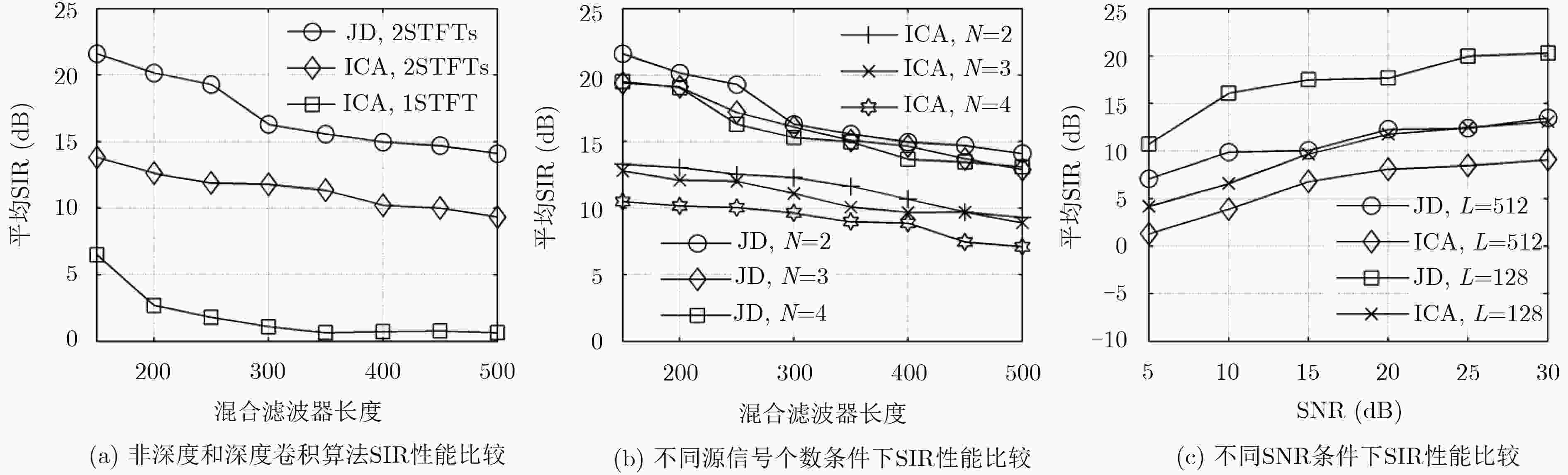
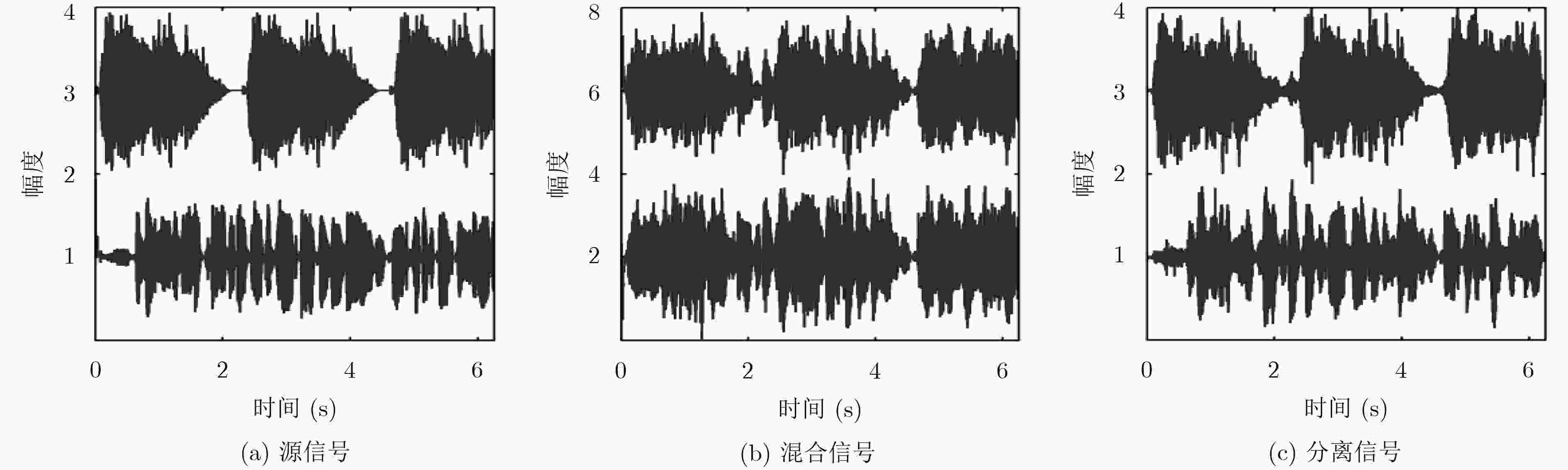
摘要: 声信号在空间中的传播具有较强的多径效应,在接收端往往以卷积形式相互叠加,尤其在海洋、剧场等强混响条件下,混合滤波器冲激响应的长度会显著增加,现有的频域卷积盲分离算法将失效。为了消除长脉冲响应导致解混合模型失效的问题,该文对观测信号进行两次短时傅里叶变换(STFT),第1次STFT缩短了脉冲响应长度,第2次STFT将信号模型转化为瞬时盲分离,最终利用联合对角化(JD)技术估计出分离矩阵。与现有方法相比,所提方法解决了深度卷积混合下模型失效的问题,并且当源信号数较多或存在加性噪声时,可以得到更好的分离性能。仿真结果验证了方法的有效性和性能优势。Abstract: The propagation of acoustic signal in space has a strong multipath effect, and the receiver often overlaps in the form of convolution. Especially in strong reverberation conditions such as ocean and theatre, where the length of impulse response of hybrid filter increases significantly. In order to eliminate the problem that long impulse response leads to the failure of the frequency domain convolution blind separation algorithm, two Short-Time Fourier Transforms (STFT) are applied to the observed signal. The first STFT shortens the length of the hybrid filter. The second STFT converts the signal model into instantaneous blind separation. Finally, the separation matrix is estimated by Joint Diagonalization (JD) technique. Compared with the existing methods, this method solves the problem of model failure under deep convolution mixing, and can obtain better separation performance when the number of source signals is large or additive noise exists. The simulation results verify the effectiveness and performance advantages of the proposed method.
-
表 1 不同源信号数情况下调整排序混乱前后SIR对比(dB)
分离性能 信源个数 2 3 4 调序前 3.4 1.5 1.2 调序后 15.4 14.9 14.3 -
BUCHNER H, AICHNER R, and KELLERMANN W. A generalization of blind source separation algorithms for convolutive mixtures based on second-order statistics[J]. IEEE Transactions on Speech and Audio Processing, 2005, 13(1): 120–134. doi: 10.1109/TSA.2004.838775 张华, 冯大政, 庞继勇. 基于二阶统计量的语音信号时域卷积盲分离算法[J]. 电子与信息学报, 2010, 32(5): 1083–1087. doi: 10.3724/SP.J.1146.2009.00574ZHANG Hua, FENG Dazheng, and PANG Jiyong. A time-domain blind convolutive separation algorithm for speech signals based on second-order statistic[J]. Journal of Electronics &Information Technology, 2010, 32(5): 1083–1087. doi: 10.3724/SP.J.1146.2009.00574 CHERRAK O, GHENNIOUI H, THIRION-MOREAU N, et al. Preconditioned optimization algorithms solving the problem of the non unitary joint block diagonalization: Application to blind separation of convolutive mixtures[J]. Multidimensional Systems and Signal Processing, 2018, 29(4): 1373–1396. doi: 10.1007/s11045-017-0506-8 RAHBAR K and REILLY J P. A frequency domain method for blind source separation of convolutive audio mixtures[J]. IEEE Transactions on Speech and Audio Processing, 2005, 13(5): 832–844. doi: 10.1109/TSA.2005.851925 付卫红, 张琮. 基于步长自适应的独立向量分析卷积盲分离算法[J]. 电子与信息学报, 2018, 40(9): 2158–2164. doi: 10.11999/JEIT171156FU Weihong and ZHANG Cong. Independent vector analysis convolutive blind separation algorithm based on step-size adaptive[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2158–2164. doi: 10.11999/JEIT171156 YU Meng, XIN J, QI Yingyong, et al. A nonlocally weighted soft-constrained natural gradient algorithm and blind separation of strongly reverberant speech mixtures[C]. The 43rd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 2009: 346–350. WANG Lin, DING Heping, and YIN Fuliang. Combining superdirective beamforming and frequency-domain blind source separation for highly reverberant signals[J]. EURASIP Journal on Audio, Speech, and Music Processing, 2010, 2010(1): 797962. doi: 10.1155/2010/797962 SANZ-ROBINSON J, HUANG Liechao, MOY T, et al. Robust blind source separation in a reverberant room based on beamforming with a large-aperture microphone array[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 2016: 440–444. doi: 10.1109/ICASSP.2016.7471713. HIROE A. Blind Vector Deconvolution: Convolutive Mixture Models in Short-time Fourier Transform Domain[M]. DAVIES M E, JAMES C J, ABDALLAH S A, et al. Independent Component Analysis and Signal Separation. Berlin, Germany, 2007: 471–479. doi: 10.1007/978-3-540-74494-8_59. 顾凡, 王惠刚, 李虎雄. 一种强混响环境下的盲语音分离算法[J]. 信号处理, 2011, 27(4): 534–540. doi: 10.3969/j.issn.1003-0530.2011.04.009GU Fan, WANG Huigang, and LI Huxiong. A blind speech separation algorithm with strong reverberation[J]. Signal Processing, 2011, 27(4): 534–540. doi: 10.3969/j.issn.1003-0530.2011.04.009 PHAM D T. Joint approximate diagonalization of positive definite hermitian matrices[J]. SIAM Journal on Matrix Analysis and Applications, 2001, 22(4): 1136–1152. doi: 10.1137/S089547980035689X ZENG Tiaojun, GOU Li, and WU Junhang. Non-orthogonal joint diagonalization algorithm preventable ill conditioned solutions for blind source separation[J]. Optik, 2017, 140: 145–150. doi: 10.1016/j.ijleo.2017.04.011 ASAMIZU T, SAITO S, OISHI K, et al. Overdetermined blind source separation using approximate joint diagonalization[C]. The 60th IEEE International Midwest Symposium on Circuits and Systems, Boston, USA, 2017: 168–171. ZHANG Weitao and SUN Jinling. Nonunitary joint diagonalization for overdetermined convolutive blind signal separation[C]. The 26th European Signal Processing Conference, Rome, Italy, 2018: 1232–1236. doi: 10.23919/EUSIPCO.2018.8553132. 张天骐, 张华伟, 刘董华, 等. 基于区域增长校正的频域盲源分离排序算法[J]. 电子与信息学报, 2019, 41(3): 580–587. doi: 10.11999/JEIT180386ZHANG Tianqi, ZHANG Huawei, LIU Donghua, et al. Frequency domain blind source separation permutation algorithm based on regional growth correction[J]. Journal of Electronics &Information Technology, 2019, 41(3): 580–587. doi: 10.11999/JEIT180386 JAYARMAN D S, SITARAMAN G, and SESHADRI R. Blind source separation of acoustic mixtures using time-frequency domain independent component analysis[C]. The 8th International Conference on Communication Systems, Singapore, Singapore, 2002: 1016–1019. doi: 10.1109/ICCS.2002.1183286. -





 下载:
下载:


 下载:
下载:
