New Coding Scheduling Strategy Based on Virtual Queuein Wireless Multicast Network
-
摘要:
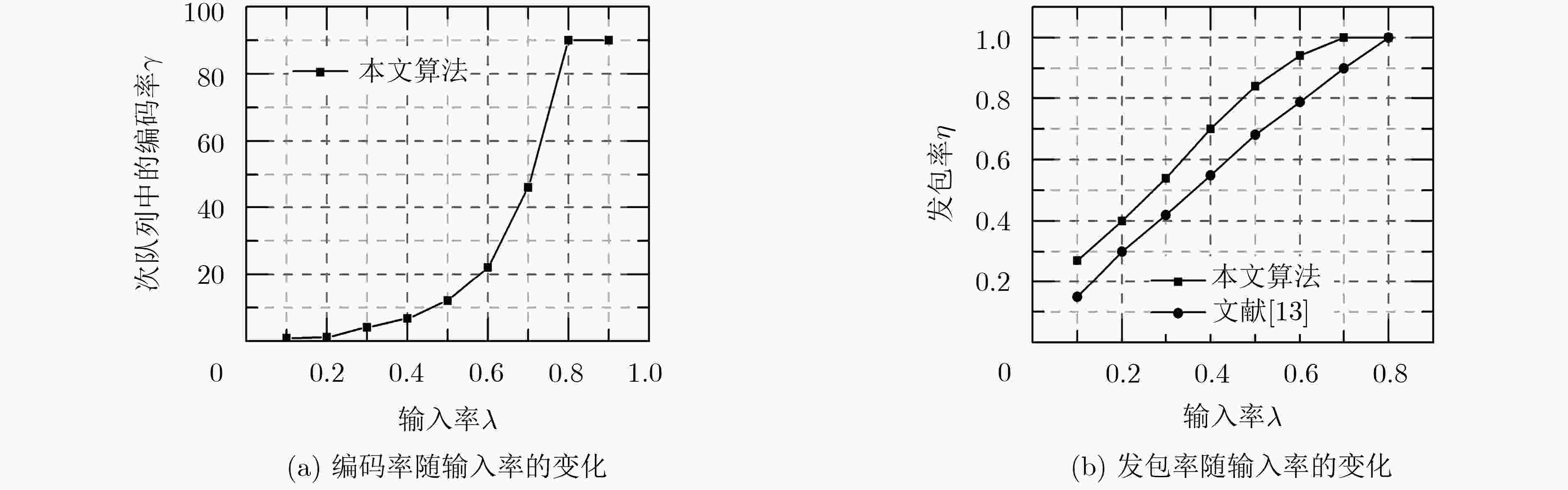
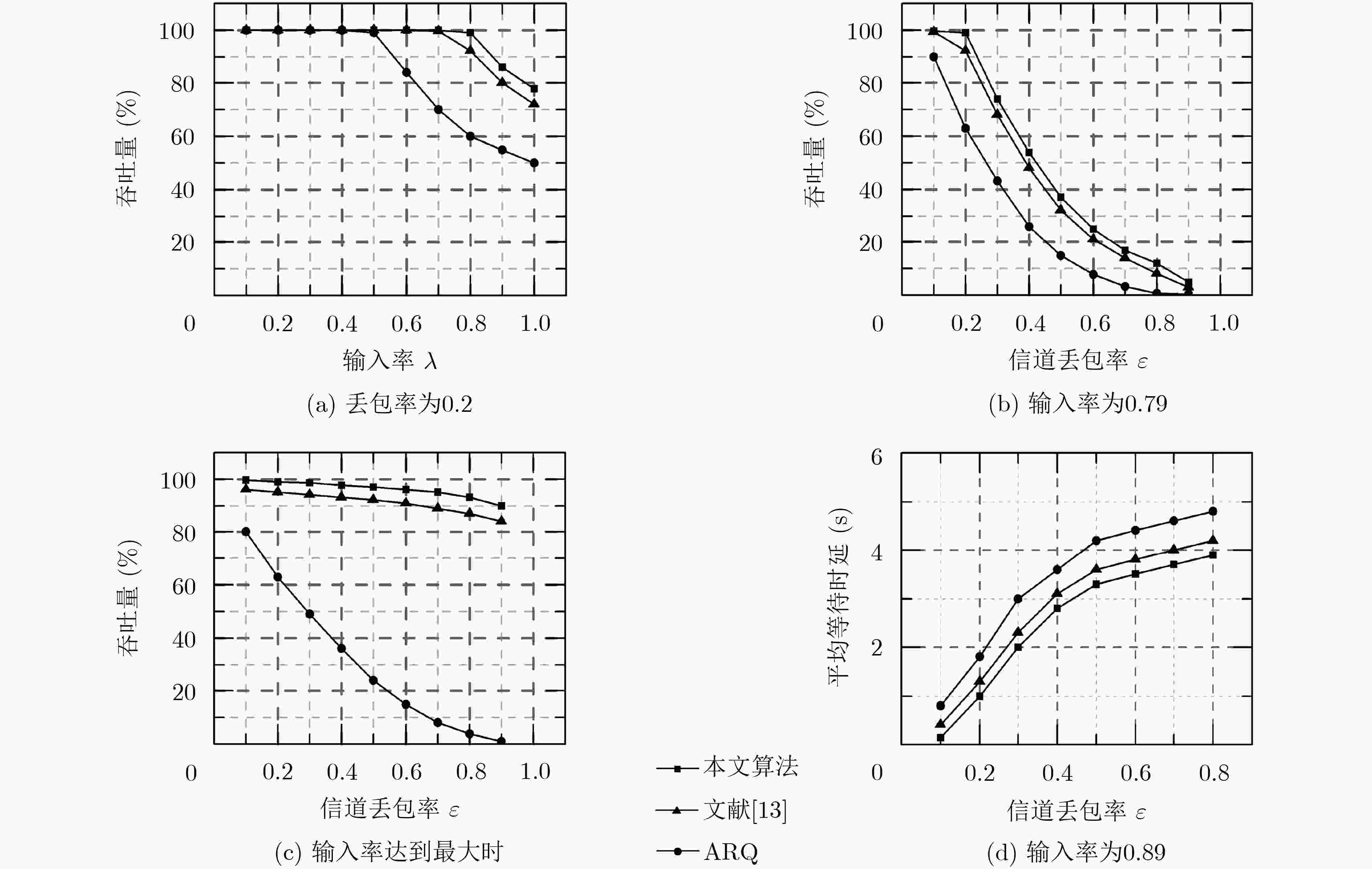
网络编码由于其传输效率高的特性,近年来在无线多播网络中得到广泛的应用。针对无线多播网络中丢包自动重传效率低的问题,该文提出一种新的基于虚拟队列中数据包到达时间的编码调度策略(CSAT)。在CSAT策略中,为了提高编码效率,采用虚拟队列来存放初始以及未被所有接收者接收到的数据包。考虑到队列的稳定性,CSAT策略按照一定的比率从主次队列选择发送;在次队列发送数据包时,结合了编码和非编码两种方式,根据数据包到达队列的先后,选取能够使较多数据包参与编码的方式发送。仿真结果表明,该文所提的CSAT编码调度策略在有效提高了数据包传输效率的同时,提高了网络的吞吐量并降低了平均等待时延。
Abstract:Network coding is widely used in wireless multicast networks in recent years due to its high transmission efficiency. To address the low efficiency of automatic retransmission caused by packet loss in wireless multicast network, a new Coding Scheduling strategy based on Arriving Time (CSAT) in virtual queue is proposed. For improving encoding efficiency, virtual queues are used to store packets that are initially generated and not received by all receivers. Considering the stability of the queue, CSAT strategy chooses to send packet from the primary and secondary queue at a certain ratio. Both encoding and non-encoding methods are combined to send in the secondary queue. According to the arrival sequence of packets in the queue, the sending method that makes more packets participate in encoding is selected. Simulation results show that the proposed CSAT not only effectively improves packet transmission efficiency, but also improves network throughput and reduces average wait delay.
-
Key words:
- Network coding /
- Virtual queue /
- Wireless multicast network /
- Automatic retransmission /
- Throughput
-
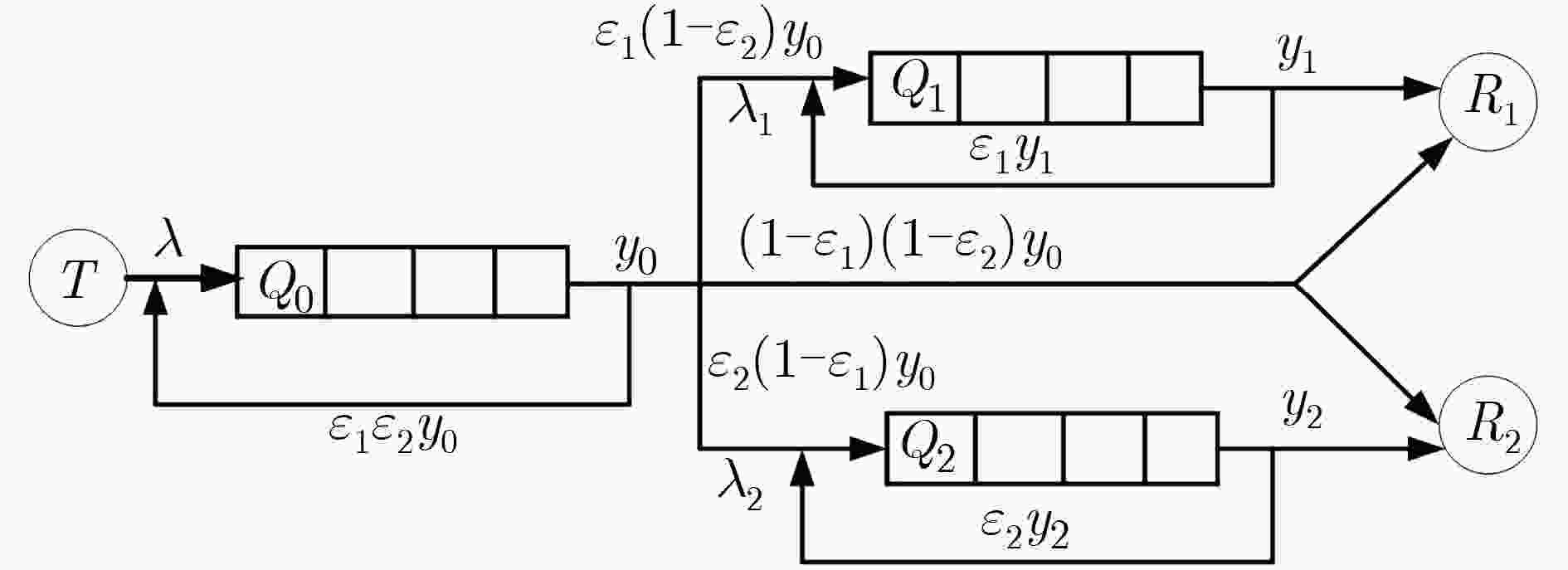
表 1 3个接收者时的网络编码策略
队列编号 Q0 Q1 Q2 Q3 Q4 Q5 Q6 索引集合 {1, 2, 3} {1, 2} {2, 3} {1, 3}} {1} {2} {3} NC0 1 0 0 0 0 0 0 NC1 0 0 0 0 1 1 1 NC2 0 1 0 0 0 0 1 NC3 0 0 1 0 1 0 0 NC4 0 0 0 1 0 1 0 表 2 CSAT调度策略流程
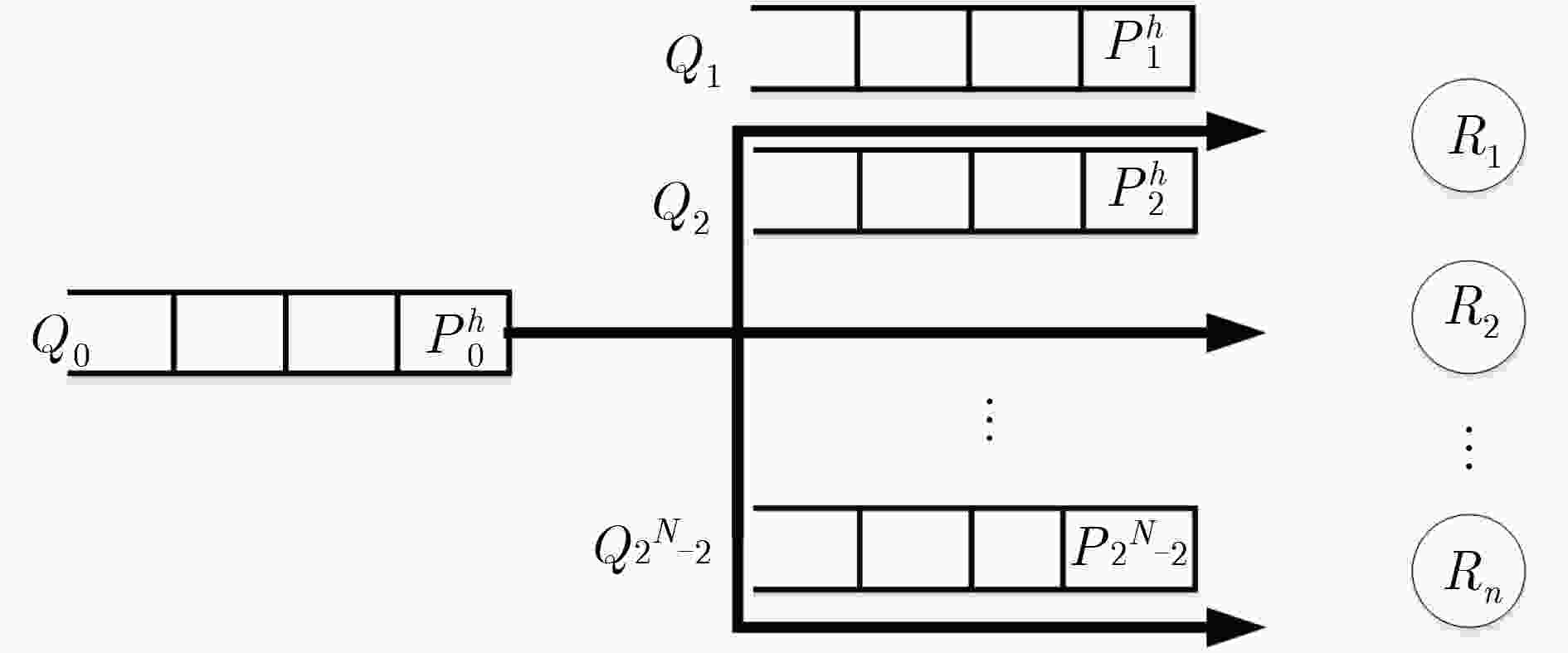
输入: 队列Qi(0 ≤ i ≤ 6), QT ={Qi|0 ≤ i ≤ 6},主队列为Q0,次队列为Qi(1 ≤ i ≤ 6), $P_i^h $表示队列Qi的队首数据包,索引集合为I={Ri|1
≤ i ≤ 3}, $I_i^h $表示Qi队首数据包的索引集合,Ri表示接收者i,编码方式表示为NCk(1 ≤ k ≤ 4),主次队列发送比为m/n,令flag1=
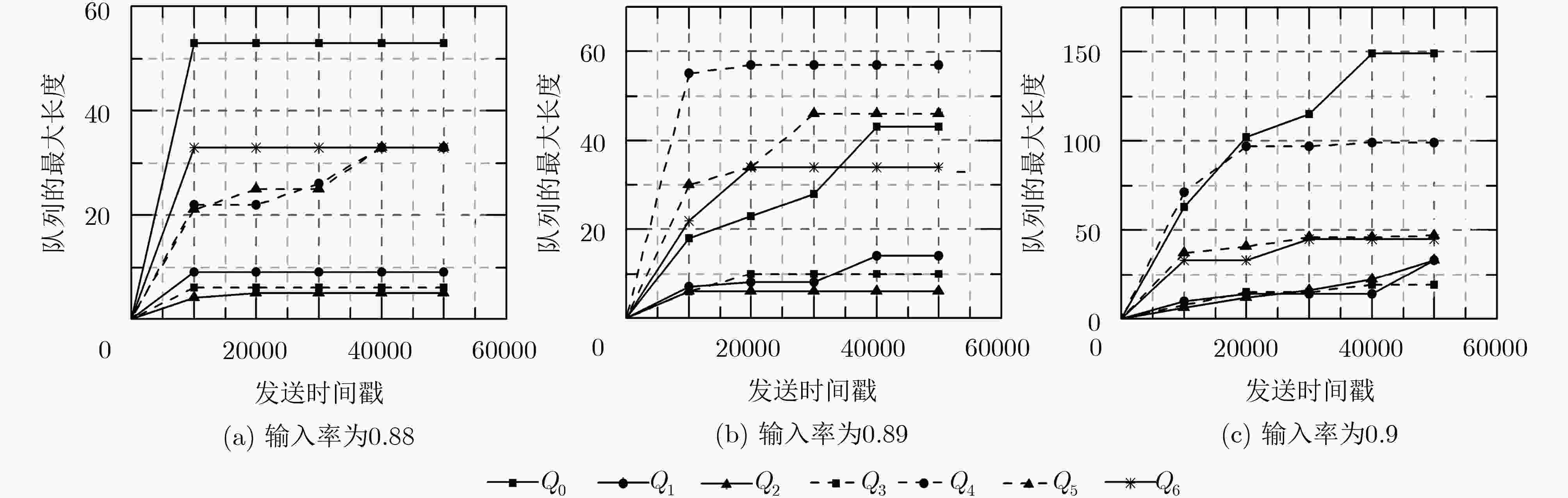
0, flag2=0。输出: 每个队列的最大长度max(Qi),被所有接收者成功接收到的数据包的个数num,每个时隙发送数据包的个数的和sum。 步骤 1 若QT 不为空,执行步骤2;否则等待数据包的到达; 步骤 2 如果Q0不为空并且flag1<m,发送队列Q0的队首数据包$P_i^h $, flag1++,根据反馈消息更新该数据包的索引集合Ihi;否则跳转步骤4; 步骤 3 如果$I_i^h $集合为空,$P_i^h $数据包被成功接收,离开该队列系统;如果$I_i^h $={R1, R2, R3}, $P_i^h $数据包没有被任何接收者接收,继续停留
队列Qi,否则该数据包将根据其索引集合进入其他队列;步骤 4 如果次队列非空并且flag2<n,选择最先到达队列的数据包$P_i^h $,寻找满足该数据包的编码方式集合{NCk|1 ≤ k ≤ 4},否则跳转步骤1; 步骤 5 如果有3个数据包参与编码的编码方式存在并且其它队列与之编码的数据包均存在,则以该编码方式发送数据包$P_i^h $, flag2++;否
则执行步骤6;步骤 6 若其它队列存在数据包与之编码发送,则以该编码方式发送数据包$P_i^h $, flag2++;否则,以非编码的方式发送数据包$P_i^h $, flag2++; 步骤 7 输出各个队列的最大长度max(Qi),被所有接收者接收到的数据包个数num以及每个时隙发送的数据包个数和sum。 表 3 在不同的丢包率下达到的最大输入率以及最优的主次队列发送比
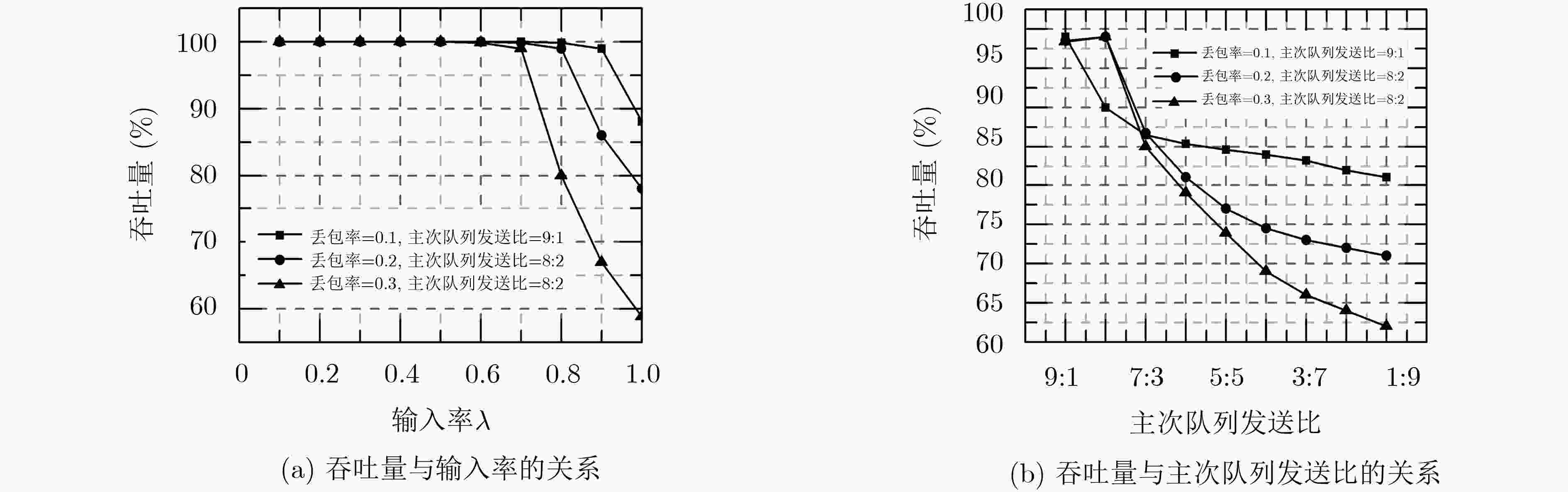
信道丢包率ε 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 主次比(m/n) 9:1 8:2 8:2 7:3 6:4 5:5 7:3 7:3 7:3 最大输入率(λ) 0.89 0.79 0.69 0.59 0.49 0.39 0.3 0.2 0.1 -
AHLSWEDE R, CAI Ning, LI S Y R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204–1216. doi: 10.1109/18.850663 AMERIMEHR M H, ASHTIANI F, and VALAEE S. Maximum stable throughput of network-coded multiple broadcast sessions for wireless tandem random access networks[J]. IEEE Transactions on Mobile Computing, 2014, 13(6): 1256–1267. doi: 10.1109/TMC.2013.2296502 SUNDARARAJAN J K, SHAH D, MÉDARD M, et al. Feedback-based online network coding[J]. IEEE Transactions on Information Theory, 2017, 63(10): 6628–6649. doi: 10.1109/TIT.2017.2710192 CHEN Wei, LETAIEF K B, and CAO Zhigang. Buffer-aware network coding for wireless networks[J]. IEEE/ACM Transactions on Networking, 2012, 20(5): 1389–1401. doi: 10.1109/TNET.2011.2176958 SAGDUYU Y E and EPHREMIDES A. On Broadcast stability of queue-based dynamic network coding over erasure channels[J]. IEEE Transactions on Information Theory, 2009, 55(12): 5463–5487. doi: 10.1109/tit.2009.2032732 SAGDUYU Y E, GEORGIADIS L, TASSIULAS L, et al. Capacity and stable throughput regions for the broadcast erasure channel with feedback: An unusual union[J]. IEEE Transactions on Information Theory, 2013, 59(5): 2841–2862. doi: 10.1109/tit.2011.2171180 SHAO Pengfei, ZHAO Yanwei, YANG Mingxia, et al. Hash searching and network coding based constant retransmission for wireless multicast[J]. IET Communications, 2017, 11(2): 302–309. doi: 10.1049/iet-com.2016.0484 TAN Guoping, CHEN Yangjie, LI Yueheng, et al. PNCIA: An interference aware wireless multicast scheme with partial network coding[C]. 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chongqing, China, 2016: 155–159. doi: 10.1109/ITNEC.2016.7560339. MOHANDESPOUR M, GOVINDARASU M, and WANG Zhengdao. Rate, energy, and delay tradeoffs in wireless multicast: network coding versus routing[J]. IEEE Transactions on Mobile Computing, 2016, 15(4): 952–963. doi: 10.1109/TMC.2015.2439258 LI Yuzhou, SHI Yan, SHENG Min, et al. Energy-efficient transmission in heterogeneous wireless networks: A delay-aware approach[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7488–7500. doi: 10.1109/TVT.2015.2472578 MOGHADAM N and LI Hongxiang. Improving queue stability in wireless multicast with network coding[C]. 2015 IEEE International Conference on Communications, London, UK, 2015: 3382–3387. doi: 10.1109/ICC.2015.7248847. MOGHADAM N and LI Hongxiang. Queue stability analysis in network coded wireless multicast network[J]. IEEE Communications Letters, 2016, 20(5): 950–953. doi: 10.1109/LCOMM.2016.2524453 MOGHADAM N and LI Hongxiang. A new wireless multicast queuing design using network coding and data-flow model[J]. IEEE Communications Letters, 2016, 20(8): 1603–1606. doi: 10.1109/LCOMM.2016.2568212 BÓNA M. Introduction to Enumerative Combinatorics[M]. Boston: McGraw-Hill, 2007: 63–70. 杨雅琴. 第二类Stirling数计算公式的一种证明[J]. 青岛科技大学学报: 自然科学版, 2009, 30(4): 369–371. doi: 10.3969/j.issn.1672-6987.2009.04.023YANG Yaqin. The proof for formula of stirling numbers of the second-kind[J]. Journal of Qingdao University of Science and Technology:Natural Science Edition, 2009, 30(4): 369–371. doi: 10.3969/j.issn.1672-6987.2009.04.023 -





 下载:
下载:



 下载:
下载:
