Fully Digital Feedforward Background Calibration of Time Skew for Sub-Sampling Time-interleaved Analog-to-digital Converter
-
摘要:
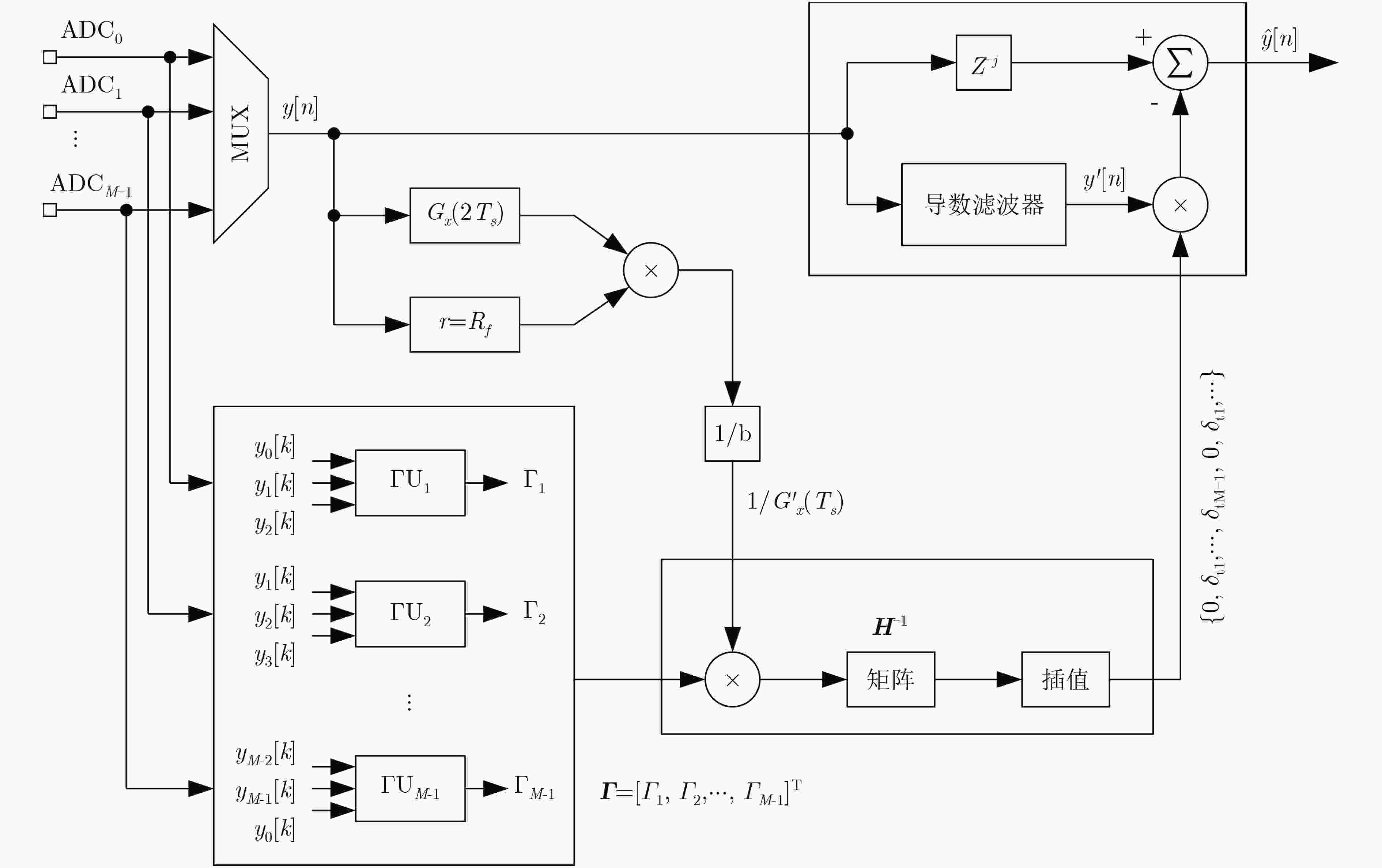
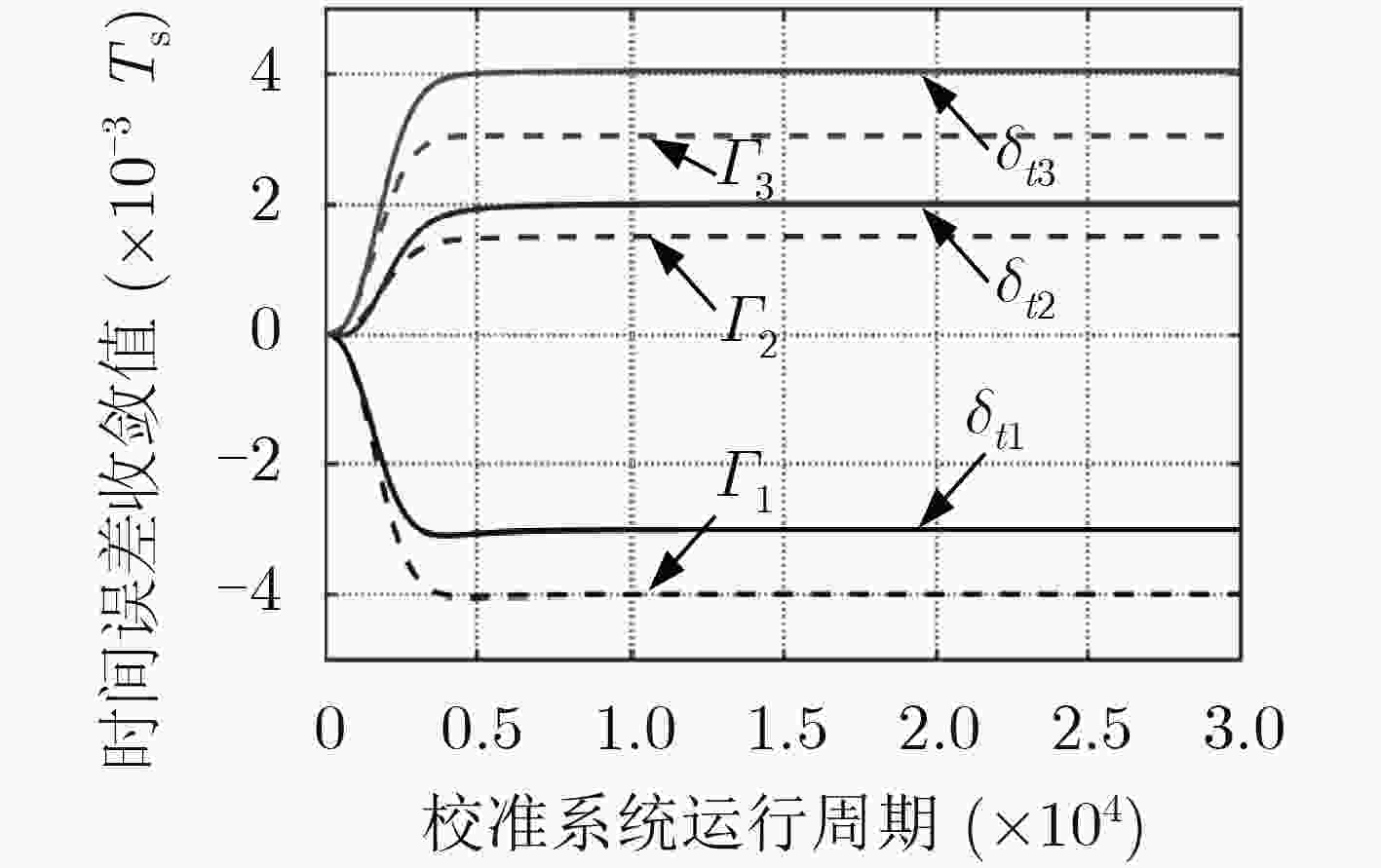
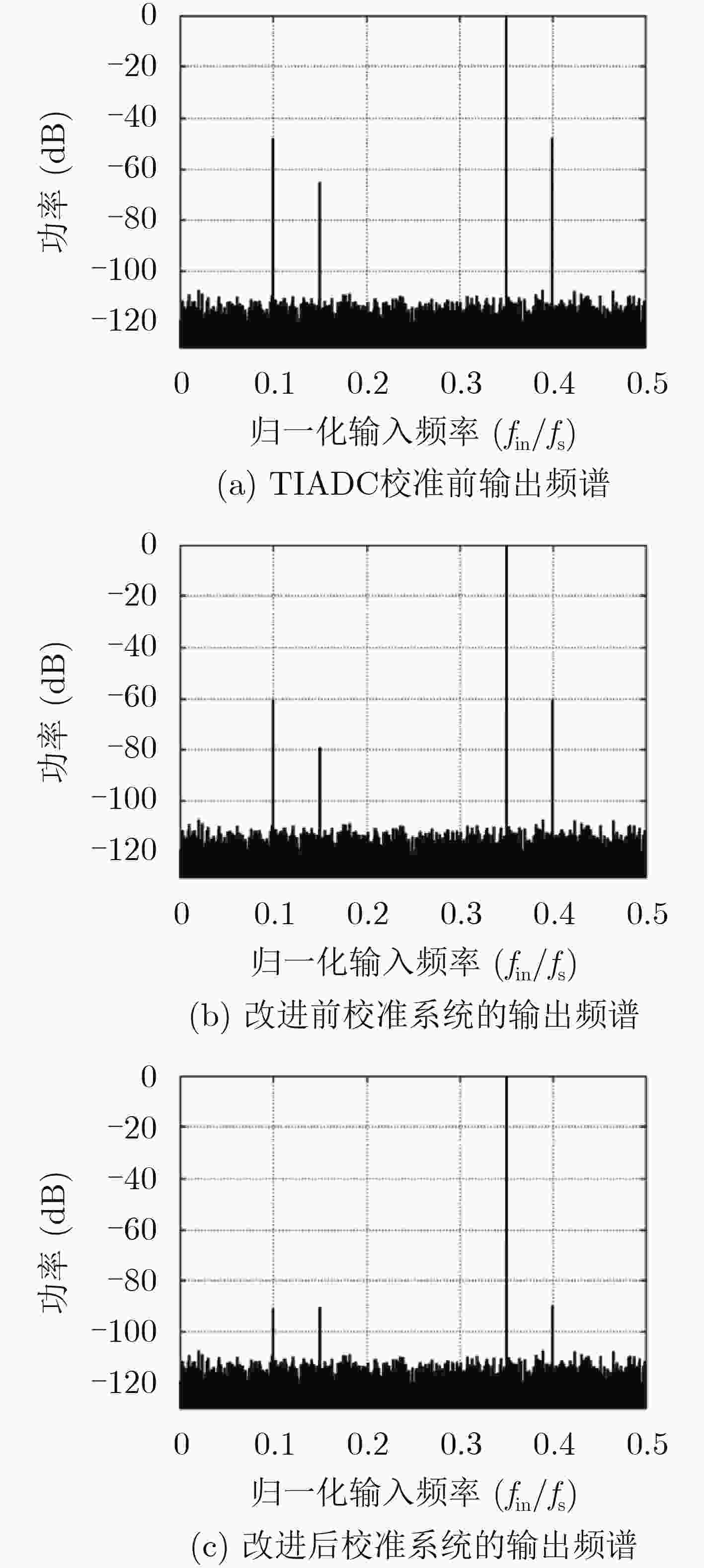
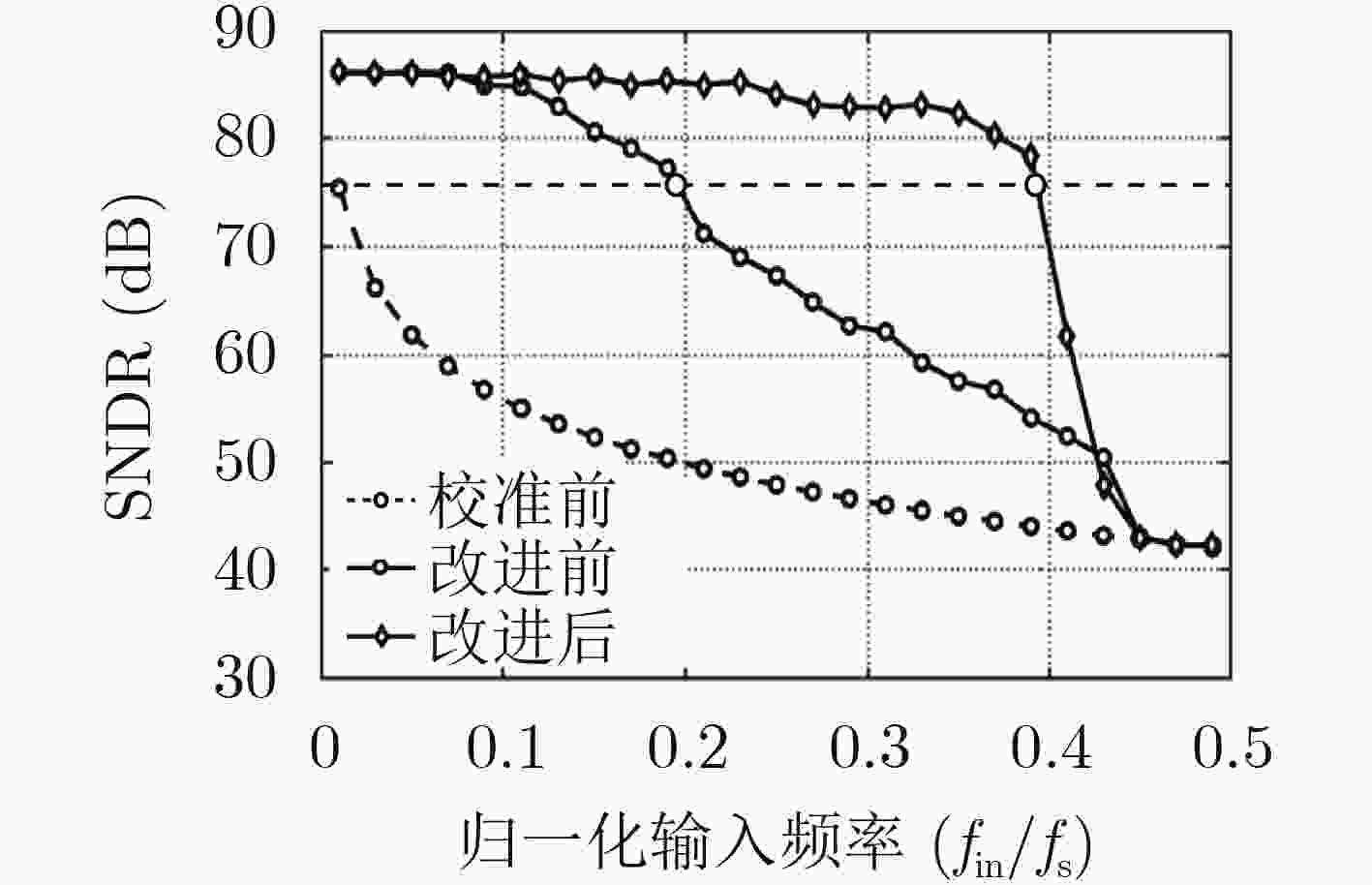
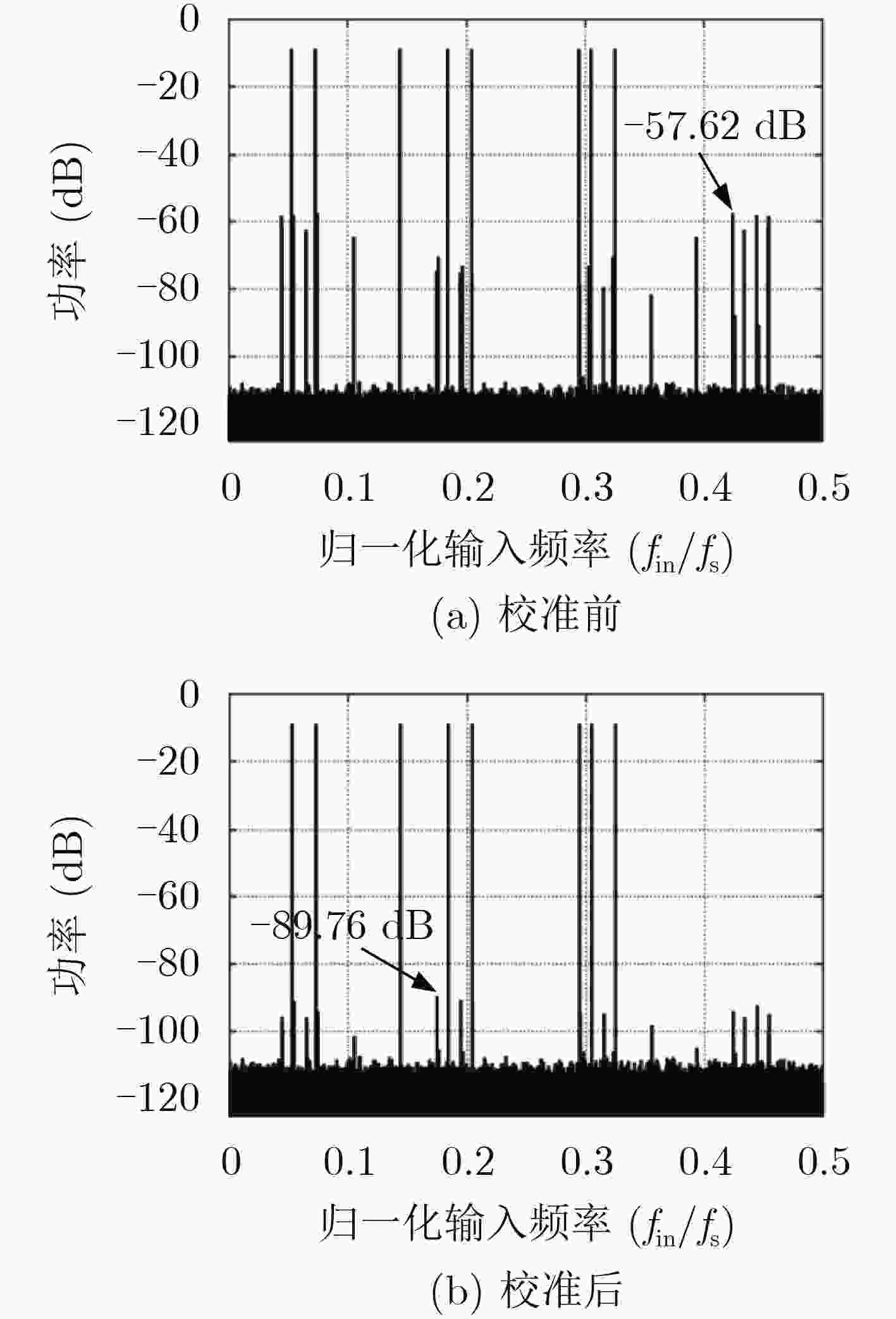
该文设计实现了一种全数字前馈式时间交织模数转换器(TIADC)时间误差校准算法,其中采样时间误差提取采用改进的时间误差函数求导模块的前馈式提取方法,可以提高在输入信号频率较高时误差提取的准确度;同时,为了降低误差提取单元的复杂性,采用了以减法实现的时间误差函数;最后,采用基于1阶泰勒补偿完成时间误差的实时校正。仿真验证表明,应用于4通道14位TIADC系统,当输入信号为多频信号时,系统动态性能无杂散动态范围(SFDR)从48.6 dB提高到80.7 dB。与传统基于前馈校准结构对比,可以将有效校准输入信号带宽从0.19提高到0.39,提高了校准算法的应用范围。
Abstract:A full digital feedforward Time-Interleaved Analog-to-Digital Converter (TIADC) time skew calibration algorithm is presented, the time skew estimation adopts the feedforward extraction method of the improved derivative module of time skew function, which can greatly improve the accuracy of skew estimation when the input signal frequency is high. At the same time, the time skew function is based on subtraction, in order to reduce the complexity of skew estimation unit. Finally, the time skew is corrected by using first-order Taylor compensation. The simulation results show that when the input signal is a multi-frequency signal, the Spurious-Free Dynamic Range (SFDR) increases from 48.6 dB to 80.7 dB, after adopting the proposed time skew correction for a 4-channal 14-bit TIADC system. Compared with the traditional feedforward calibration structure based on correlation operation, the effective calibration input signal bandwidth can be increased from 0.19 to 0.39, which greatly increases the application range of the calibration algorithm.
-
表 1 归一化输入频率为0.35时,校准前后性能参数表
SNDR (dB) SFDR (dB) ENOB (bit) 校准前 44.89 47.94 7.16 改进前 57.54 60.56 9.27 改进后 82.90 89.94 13.48 -
RAZAVI B. Design considerations for interleaved ADCs[J]. IEEE Journal of Solid-State Circuits, 2013, 48(8): 1806–1817. doi: 10.1109/JSSC.2013.2258814 BLACK W and HODGES D. Time interleaved converter arrays[C]. 1980 IEEE International Solid-State Circuits Conference. Digest of Technical Papers, San Francisco, USA, 1980: 14–15. EL-CHAMMAS M and MURMANN B. General analysis on the impact of phase-skew in time-interleaved ADCs[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2009, 56(5): 902–910. doi: 10.1109/TCSI.2009.2015206 STEPANOVIC D and NIKOLIC B. A 2.8 GS/s 44.6 mW time-interleaved ADC achieving 50.9 dB SNDR and 3 dB effective resolution bandwidth of 1.5 GHz in 65 nm CMOS[J]. IEEE Journal of Solid-State Circuits, 2013, 48(4): 971–982. doi: 10.1109/JSSC.2013.2239005 WANG Xiao, LI Fule, JIA Wen, et al. A 14-bit 500-MS/s time-interleaved ADC with autocorrelation-based time skew calibration[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2019, 66(3): 322–326. doi: 10.1109/TCSII.2018.2849691 STRAAYER M, BALES J, BIRDSALL D, et al. 27.5 A 4 GS/s time-interleaved RF ADC in 65 nm CMOS with 4 GHz input bandwidth[C]. The 2016 IEEE International Solid-state Circuits Conference, San Francisco, USA, 2016: 464–465. BENABES P, LELANDAIS-PERRAULT C, and LE DORTZ N. Mismatch calibration methods for high-speed time-interleaved ADCs[C]. The 12th IEEE International New Circuits and Systems Conference, Trois-Rivieres, Canada, 2014: 49–52. WANG Yongsheng, LI Shanshan, WANG Ruoyang, et al. LMS-FIR based digital background calibration for the four-channel time-interleaved ADC[C]. The 12th IEEE International Conference on ASIC, Guiyang, China, 2017: 391–394. LE DUC H, NGUYEN D M, JABBOUR C, et al. All-digital calibration of timing skews for TIADCs using the polyphase decomposition[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2016, 63(1): 99–103. doi: 10.1109/TCSII.2015.2483423 LIN C Y, WEI Y H, and LEE T C. A 10-bit 2.6-GS/s time-interleaved SAR ADC with a digital-mixing timing-skew calibration technique[J]. IEEE Journal of Solid-state Circuits, 2018, 53(5): 1508–1517. doi: 10.1109/JSSC.2018.2793535 QIU Yongtao, ZHOU Jie, LIU Youjiang, et al. An adaptive blind calibration technique for frequency response mismatches in M-channel time-interleaved ADCs[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2019, 66(4): 702–706. doi: 10.1109/TCSII.2018.2871108 LE DORTZ N, BLANC J P, SIMON T, et al. 22.5 A 1.62 GS/s time-interleaved SAR ADC with digital background mismatch calibration achieving interleaving spurs below 70 dBFS[C]. The 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers, San Francisco, USA, 2014: 386–388. LE DORTZ N, SIMON T, URARD P, et al. Method and device for use with analog to digital converter[P]. USA, US2014232575, 2014-11-18. LE DUC H, NGUYEN D M, JABBOUR C, et al. Hardware implementation of all digital calibration for undersampling TIADCs[C]. The 2015 IEEE International Symposium on Circuits and Systems, Lisbon, Portugal, 2015: 2181–2184. SALIB A, CARDIFF B, and FLANAGAN M F. A low-complexity correlation-based time skew estimation technique for time-interleaved SAR ADCs[C]. The 2017 IEEE International Symposium on Circuits and Systems, Baltimore, USA, 2017: 1–4. YEN H T, VAN T, HAN L D, et al. Background calibration of multiple channel mismatches in time-interleaved ADCs[C]. The 3rd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing, Ha Noi, Vietnam, 2019: 43–47. WEI Hegong, ZHANG Peng, SAHOO B D, et al. An 8 bit 4 GS/s 120 mW CMOS ADC[J]. IEEE Journal of Solid-State Circuits, 2014, 49(8): 1751–1761. doi: 10.1109/JSSC.2014.2313571 HARRIS F, CHEN Xiaofei, VENOSA E, et al. Two channel TI-ADC for communication signals[C]. The 12th IEEE International Workshop on Signal Processing Advances in Wireless Communications, San Francisco, USA, 2011: 576–580. CENTURELLI F, MONSURRO P, and TRIFILETTI A. Efficient digital background calibration of time-interleaved pipeline analog-to-digital converters[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2012, 59(7): 1373–1383. doi: 10.1109/TCSI.2011.2177003 -





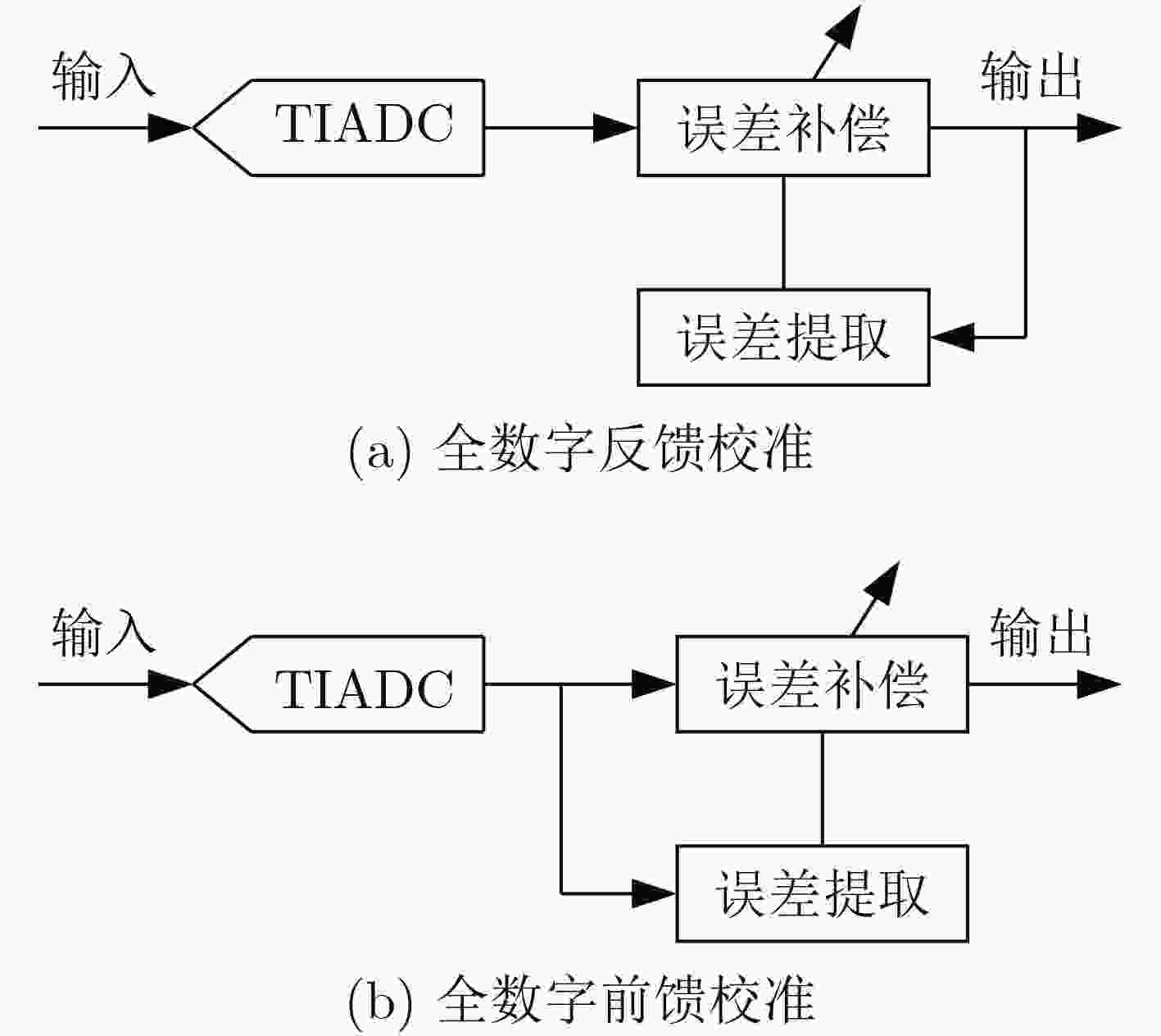
 下载:
下载:
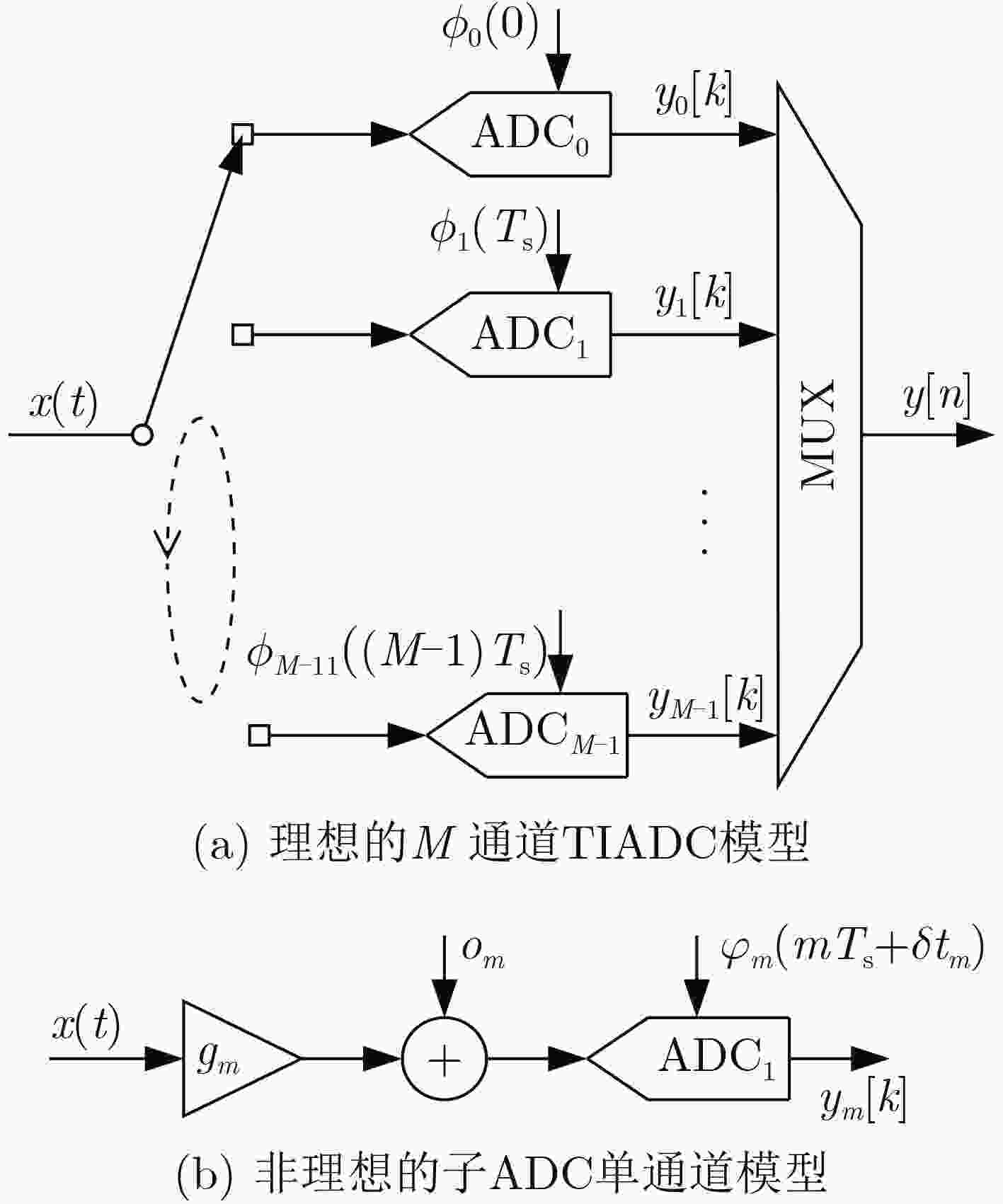
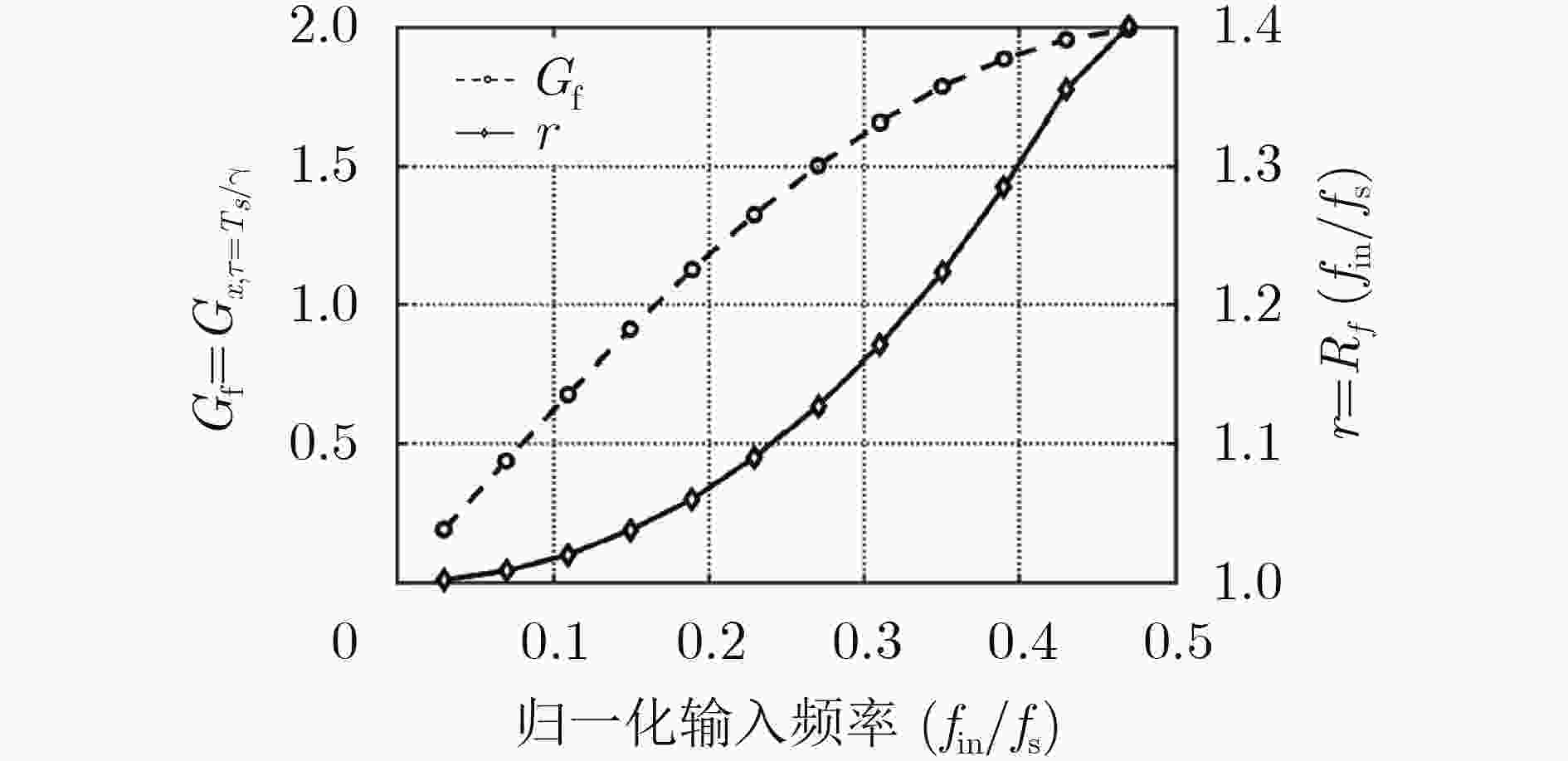
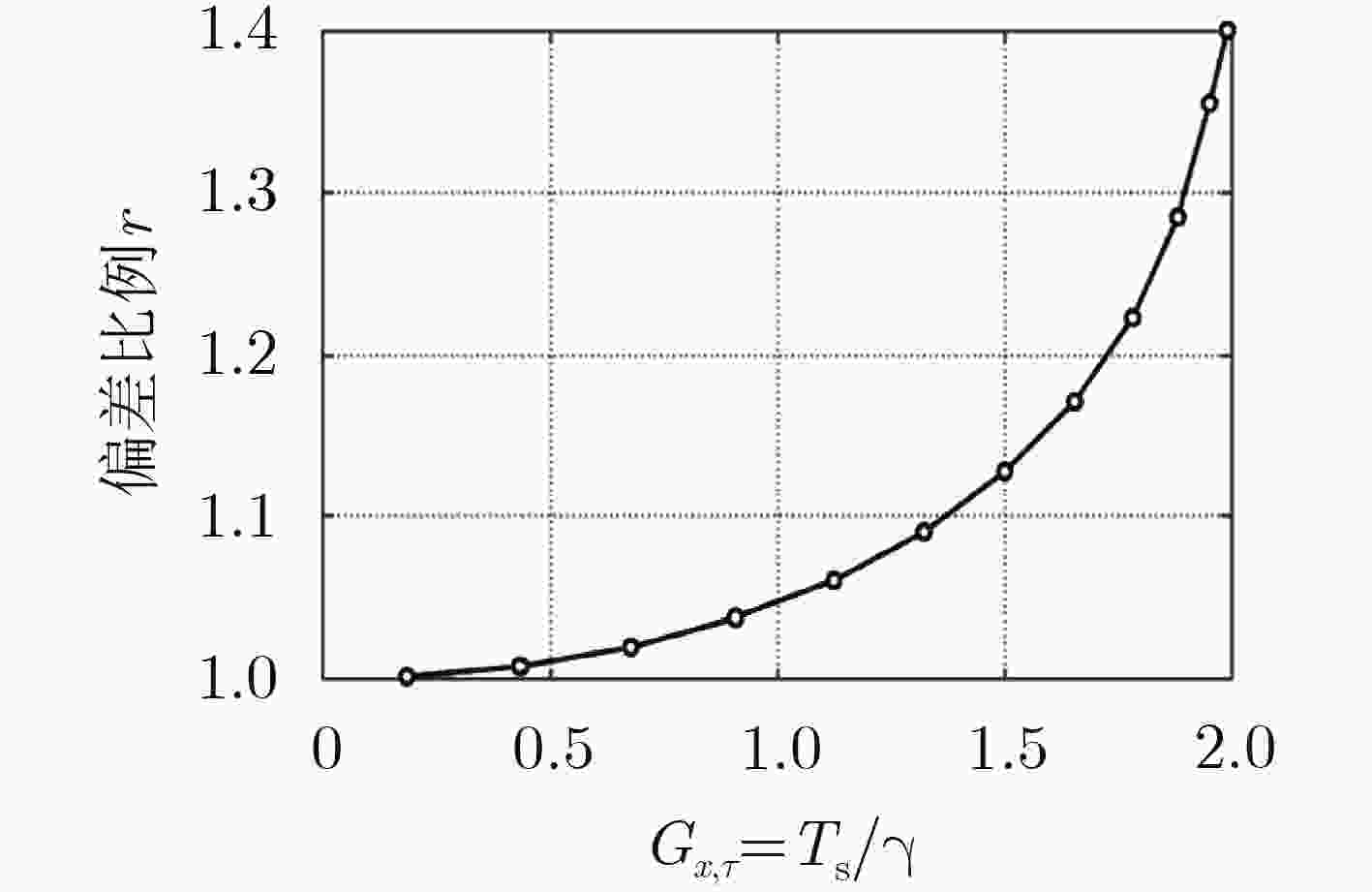



 下载:
下载:
