A New High Order Finite Difference Time Domain Method
-
摘要:
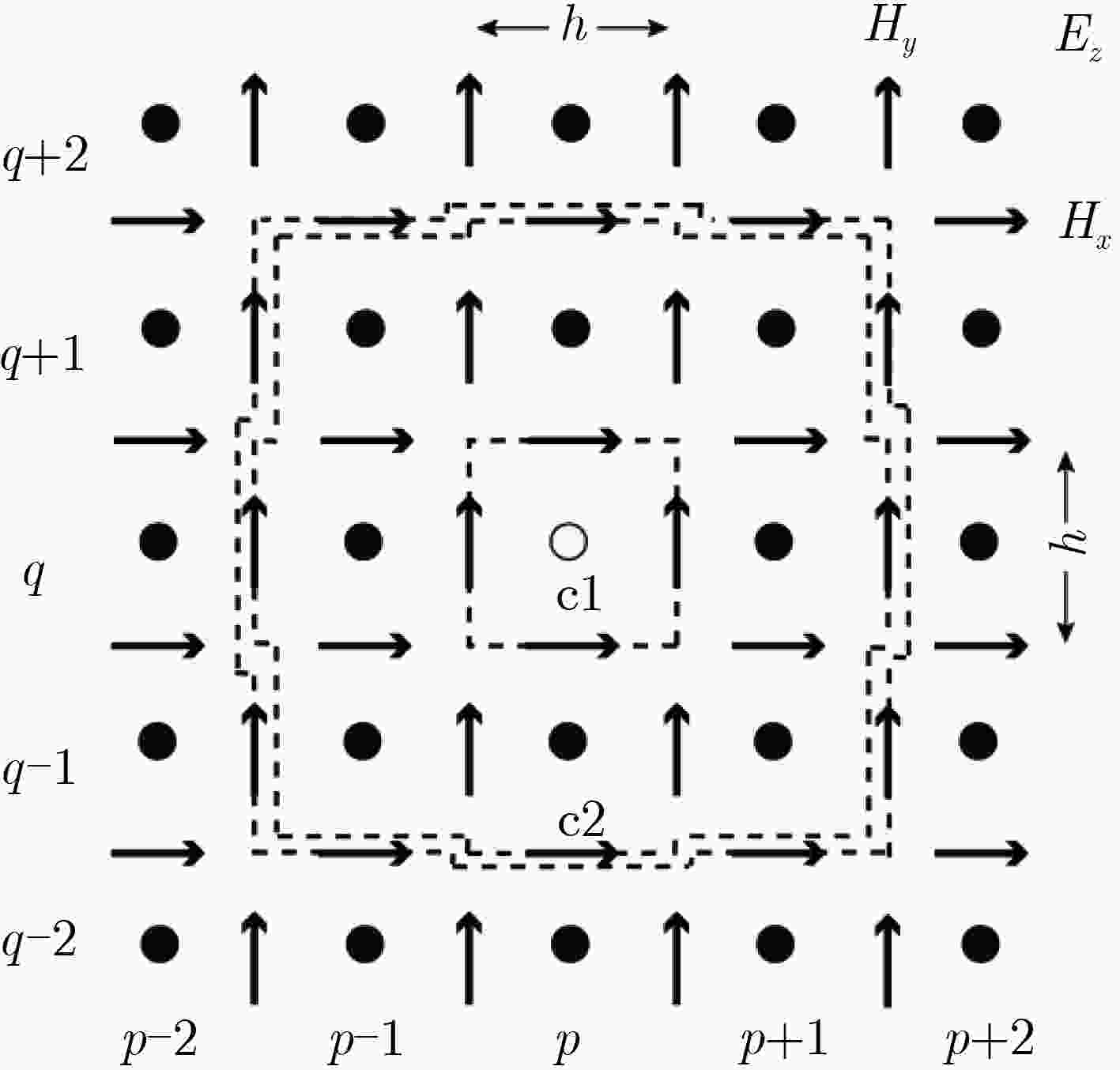
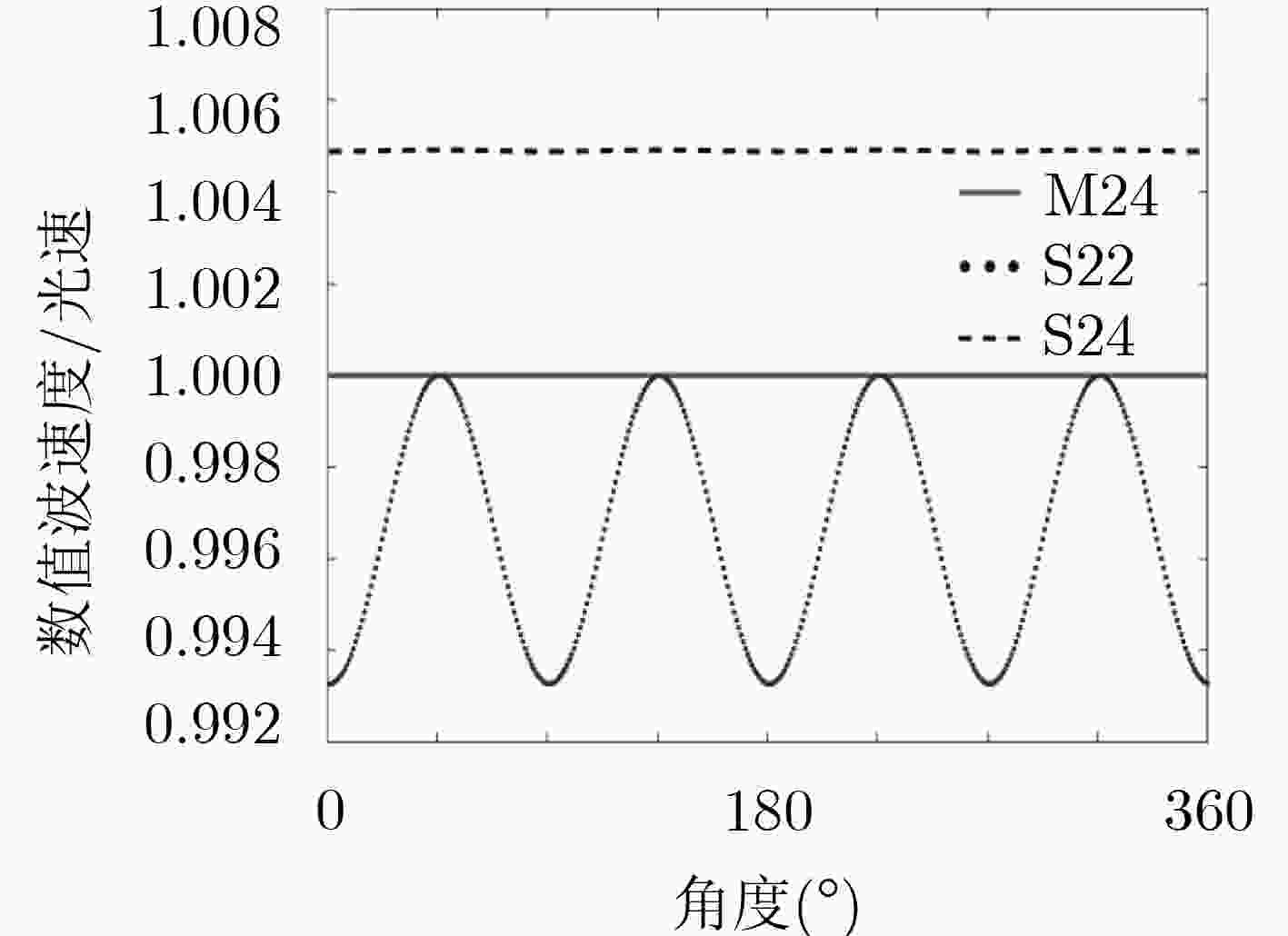
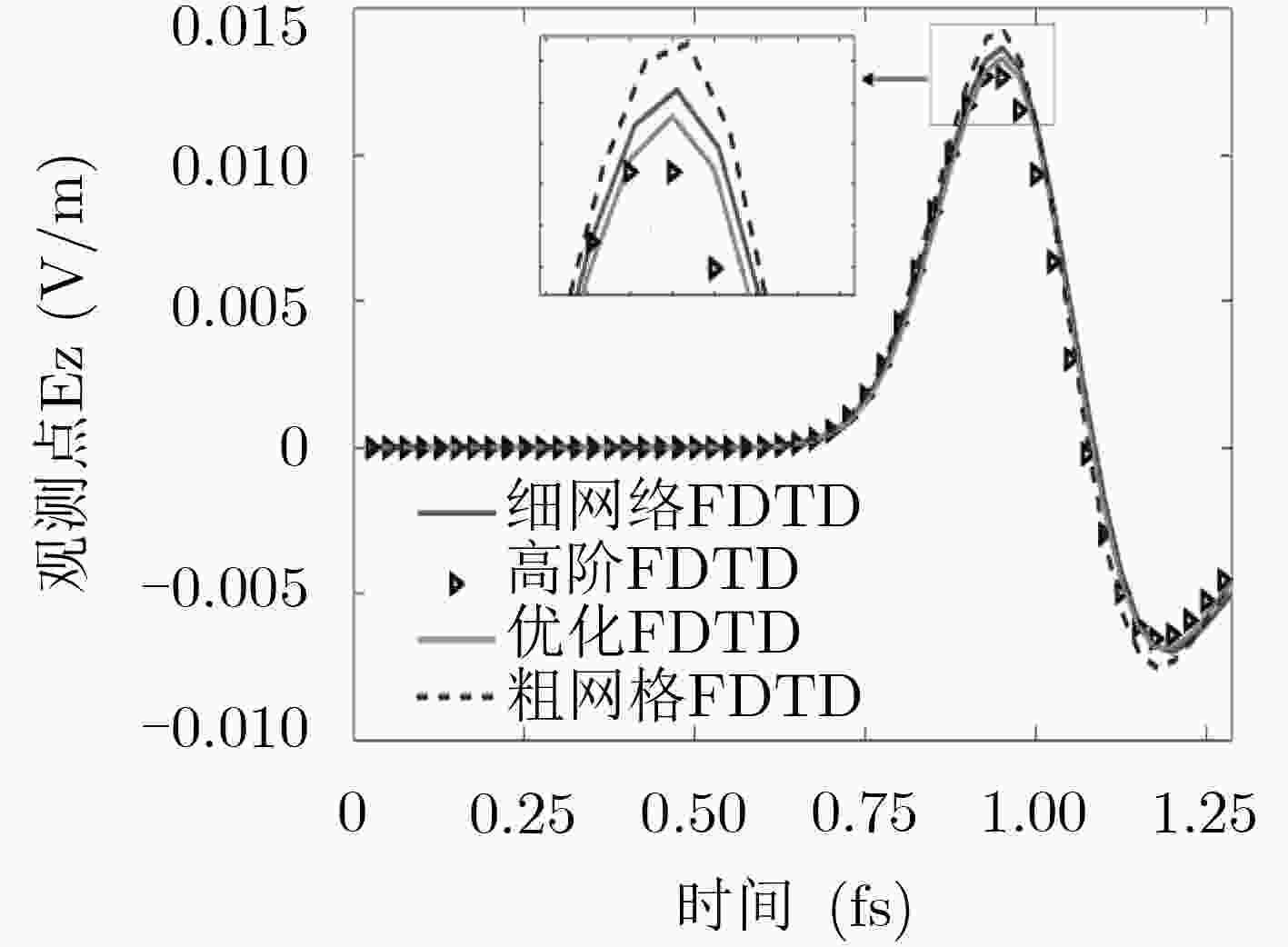
相比于传统高阶时域有限差分算法(FDTD)而言,该文提出了一种改进的高阶FDTD的优化方法,该算法基于安培环路定律,通过计算机技术寻找到一组最优的系数使得FDTD方法的全局色散误差达到最小,通过不同分辨率下的点源辐射模拟证明了该方法在较低分辨率的情况下仍然具有极低的相位误差,对于解决电大尺寸结构建模中的数值色散等问题提供了有效的解决方案。
Abstract:Compared with the traditional high-order Finite Difference Time Domain(FDTD) Method, an improved high-order FDTD optimization method is proposed in this paper. This algorithm is based on Ampere’s law of circuits and finds a set of optimal coefficients through computer technology to minimize the global dispersion error of the FDTD method.The simulation of point source radiation with different resolutions shows that this method still has very low phase error in the case of lower resolution. It provides an effective solution to the problem of numerical dispersion in the modeling of large size structures.
-
Key words:
- Finite Difference Time Domain(FDTD) /
- Phase error /
- Optimization algorithm /
- Ampere’s law
-
表 1 部分分辨率的色散误差
R K1 K2 ${\varPhi _{\gamma_i} }$ 5 –0.14493668 0.102073777 5.3797×10–10 10 –0.11619507 0.073446898 9.1959×10–14 15 –0.11180257 0.069281772 8.4433×10–16 20 –0.11032252 0.067892310 2.2994×10–17 25 –0.10964732 0.067260967 4.3034×10–18 30 –0.10928263 0.066920442 1.5703×10–19 35 –0.10906389 0.066716504 4.4814×10–20 表 2 4种情况下的运行时间和占用内存对比
FDTD
方法运行
时间(s)占用
内存(MB)空间
步长(m)时间
步长(s)粗网格 S22 0.0356 0.1 0.100 0.16×10–9 S24 0.0323 0.2 0.100 0.16×10–9 M24 0.0329 0.7 0.100 0.16×10–9 细网格 S22 77.3070 3.0 0.004 0.66×10–10 -
YEE K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media[J]. IEEE Transactions on Antennas and Propagation, 1966, 14(3): 302–307. doi: 10.1109/TAP.1966.1138693 葛德彪, 闫玉波. 电磁波时域有限差分法[M]. 2版. 西安: 西安电子科技大学出版社, 2005: 58–108.GE Debiao and YAN Yubo. Finite Difference Time Domain Method for Electromagnetic Waves[M]. 2nd ed. Xi’an: Xidian University Press, 2005: 58–108. KIM I S and HOEFER W J R. Numerical dispersion characteristics and stability factor for the TD-FD method[J]. Electronics Letters, 1990, 26(7): 485–487. doi: 10.1049/el:19900315 CANGELLARIS A C and LEE R. On the accuracy of numerical wave simulations based on finite methods[J]. Journal of Electromagnetic Waves and Applications, 1992, 6(12): 1635–1653. doi: 10.1163/156939392X00779 SHLAGER K L, MALONEY J G, RAY S L, et al. Relative accuracy of several finite-difference time-domain methods in two and three dimensions[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(12): 1732–1737. doi: 10.1109/8.273296 何四华, 吴春光, 丛滨. 基于高频方法的电大尺寸目标RCS仿真与分析[J]. 现代雷达, 2017, 39(6): 77–80. doi: 10.16592/j.cnki.1004-7859.2017.06.018HE Sihua, WU Chunguang, and CONG Bin. RCS simulation and analysis of electrically large objects based on high frequency method[J]. Modern Radar, 2017, 39(6): 77–80. doi: 10.16592/j.cnki.1004-7859.2017.06.018 杨杨, 朱劼, 邹宁, 等. 电大凸目标电磁散射的数值路径变换算法研究[J]. 电波科学学报, 2017, 32(2): 199–206. doi: 10.13443/j.cjors.2017012201YANG Yang, ZHU Jie, ZOU Ning, et al. Numerical contour deformation method for calculating the scattered field from the electrically large convex scatterers[J]. Chinese Journal of Radio Science, 2017, 32(2): 199–206. doi: 10.13443/j.cjors.2017012201 GAO Min, YANG Feng, YAN Fei, et al. Improved quasi-analytic method for transient analysis of electrically large conducting targets illuminated by a complex source beam[J]. IET Microwaves, Antennas & Propagation, 2017, 11(8): 1139–1146. doi: 10.1049/iet-map.2016.0796 HADI M F, BOLLIMUNTHA R C, ELSHERBENI A Z, et al. A spherical FDTD numerical dispersion relation based on elemental spherical wave functions[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(5): 784–788. doi: 10.1109/LAWP.2018.2816459 PEREDA J A and GRANDE A. Numerical dispersion relation for the 2-D LOD-FDTD method in lossy media[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2122–2125. doi: 10.1109/LAWP.2017.2699692 KANG Zhen, MA Xikui, and SHAO Jinghui. A low-dispersion realization of a rectangular grid with PITD method through artificial anisotropy[J]. IEEE Microwave and Wireless Components Letters, 2017, 27(4): 320–322. doi: 10.1109/LMWC.2017.2678399 ZHOU Longjian, YANG Feng, LONG Rui, et al. A hybrid method of higher-order FDTD and subgridding technique[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1261–1264. doi: 10.1109/LAWP.2015.2504448 苏卓, 谭峻东, 张俊, 等. 基于高阶时域有限差分算法的电磁波传播计算[J]. 电波科学学报, 2014, 29(3): 431–436. doi: 10.13443/j.cjors.2013060801SU Zhuo, TAN Jundong, ZHANG Jun, et al. An electromagnetic wave propagator based on higher-order FDTD method[J]. Chinese Journal of Radio Science, 2014, 29(3): 431–436. doi: 10.13443/j.cjors.2013060801 SAXENA A K and SRIVASTAVA K V. Higher order LOD-FDTD methods and their numerical dispersion properties[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(3): 1480–1485. doi: 10.1109/TAP.2017.2653758 REN Xingang, HUANG Zhixiang, WU Xianliang, et al. High-order unified symplectic FDTD scheme for the metamaterials[J]. Computer Physics Communications, 2012, 183(6): 1192–1200. doi: 10.1016/j.cpc.2012.01.021 WEI Xiaokun, SHAO Wei, SHI Shengbing, et al. An optimized higher order PML in domain decomposition WLP-FDTD method for time reversal analysis[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(10): 4374–4383. doi: 10.1109/TAP.2016.2596899 TAFLOVE A. Computational Electrodynamics: The Finite-Difference Time-Domain Method[M]. Boston: Artech House, 1995: 109–174. HADI M F. A modified FDTD (2, 4) scheme for modeling electricallylarge stuctures with high phase accuracy[D]. [Ph.D. dissertation], University of Colorado, 1996. -






 下载:
下载:
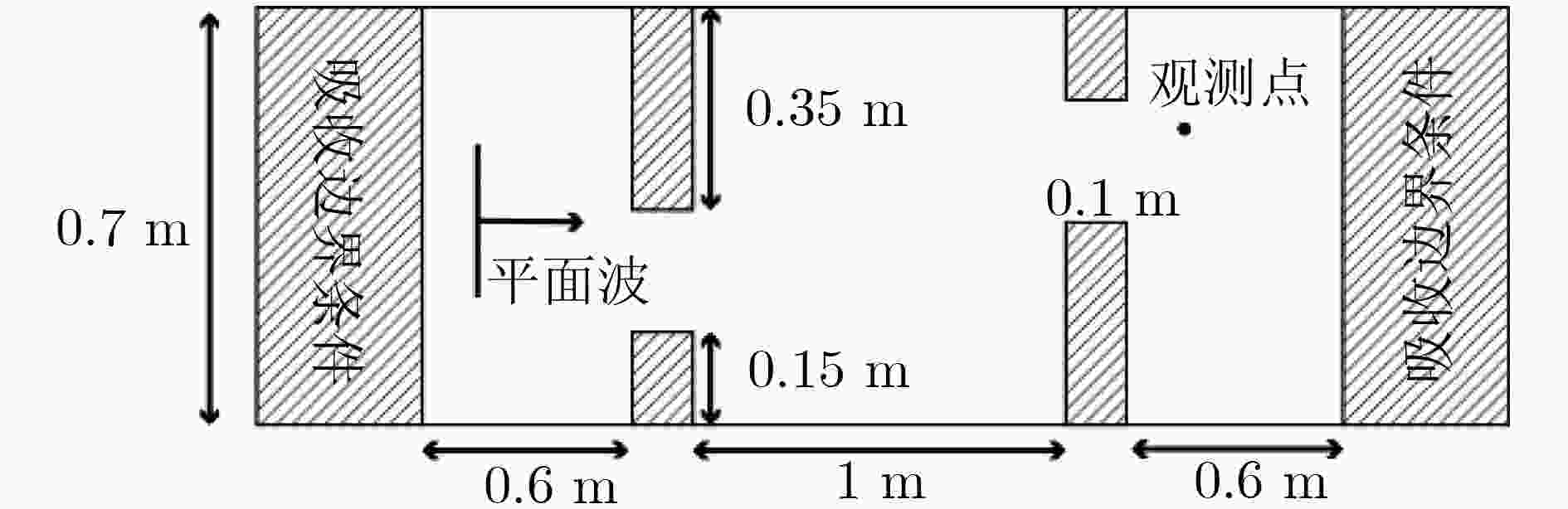
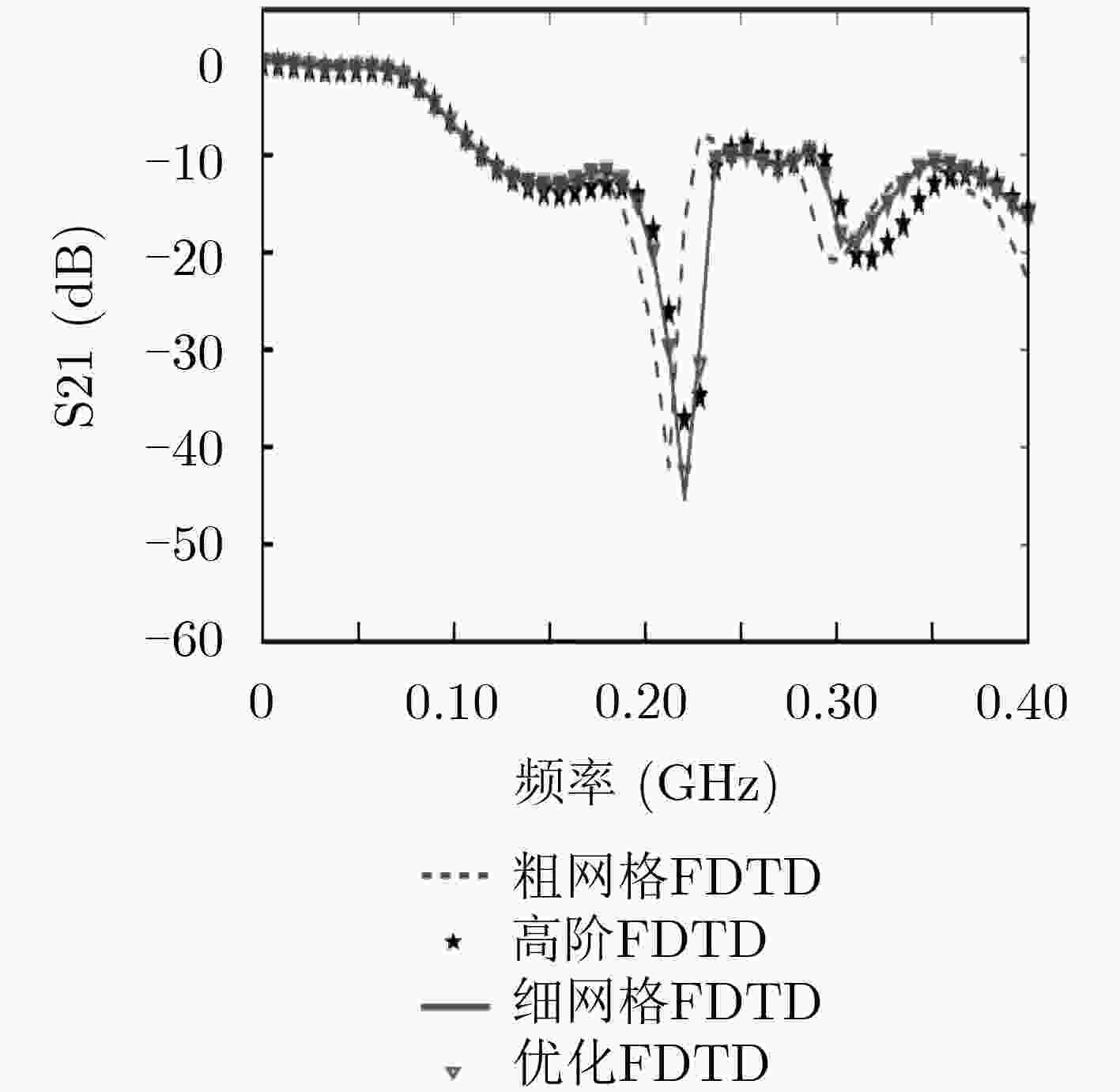


 下载:
下载:
