A Fast and Robust Design Method for Dense Focal Plane Array Feed
-
摘要: 致密焦面阵列馈源(DFPAF)融合了多喇叭多波束馈源和相控阵列馈源(PAF)的特点,与多喇叭多波束馈源和常规相控阵列馈源相比较,它可以同时提供更多的固定赋形波束进一步拓宽视场。在射电天文、雷达、电子侦察和卫星通信等领域引起了极大的关注。由于其阵列结构与常规阵列馈源不同,导致设计方法也具有特殊性,因此近年来展开了对其设计方法的研究。该文充分利用反射面天线的固有特性,并结合阵列天线理论,提出一种可以快速、稳健地设计致密焦面阵列馈源的方法,给出了设计原理和设计结果,并和最具代表性的多喇叭多波束馈源进行了性能对比分析,为设计致密焦面阵列馈电的大型反射面提供理论和数据参考。Abstract: The Dense Focal Plane Array Feed (DFPAF), which integrates the characters of multi-beam feed with multiple independent horns and Phased Array Feed (PAF), can simultaneously provide more fixed shaped beams and wider field of view than multi-beam feed with multiple independent horns and PAF. It attracts more attention in radio telescope, radar, electronic reconnaissance, satellite communication and so on. Its unique structure promotes the studies on special design method recently. Combing the theory of array antenna and inherent characteristic of parabolic reflector antenna, a fast design method with robust processing procedure is proposed in this paper. The design principle, calculated results, and comparison between DFPAF and the most representative multi-beam feed with multiple independent horns are presented. All these provide a theoretical basis and reference data for the design of giant reflector with DFPAF.
-
Key words:
- Dense focal plane array /
- Multi-beam feed /
- Reflector /
- Phased array
-
表 1 多波束反射面天线性能总结表
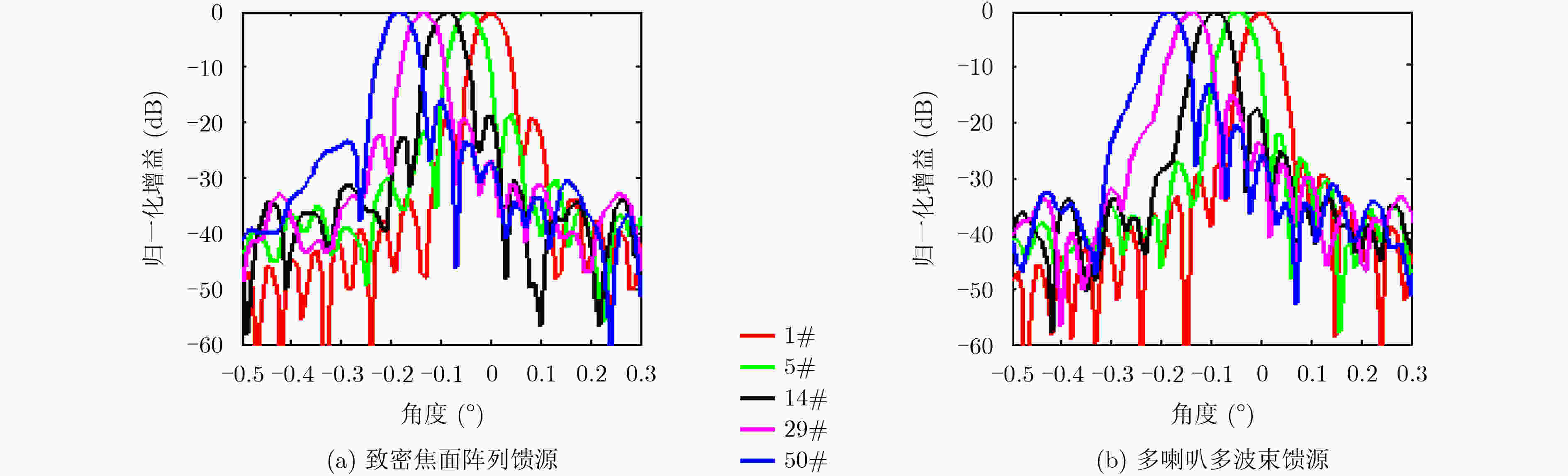
波束 馈源类型 天线增益(dB) 天线效率(%) 第1旁瓣电平(dB) 半功率波束宽度(°) 波束指向(°) 与中心波束的增益差(dB) 1号1.05 GHz 焦面场 75.08 74.00 –17.10 0.0596 0.000 0.00 多喇叭多波束馈源 74.46 64.15 –24.10 0.0612 0.000 0.00 致密焦面阵列馈源 74.98 72.32 –17.60 0.0606 0.000 0.00 5号1.05 GHz 焦面场 75.01 72.82 –16.40 0.0600 –0.045 –0.07 多喇叭多波束馈源 74.38 62.97 –19.90 0.0616 –0.045 –0.08 致密焦面阵列馈源 74.94 71.66 –16.10 0.0616 –0.045 –0.04 14号1.05 GHz 焦面场 74.92 71.32 –16.50 0.0599 –0.090 –0.16 多喇叭多波束馈源 74.20 60.47 –17.60 0.0619 –0.090 –0.26 致密焦面阵列馈源 74.74 68.43 –20.20 0.0622 –0.090 –0.24 29号1.05 GHz 焦面场 74.81 69.54 –16.40 0.0598 –0.140 –0.27 多喇叭多波束馈源 74.00 57.70 –15.40 0.0622 –0.140 –0.46 致密焦面阵列馈源 74.61 66.41 –17.10 0.0619 –0.140 –0.37 50号1.05 GHz 焦面场 74.58 65.95 –15.60 0.0617 –0.180 –0.50 多喇叭多波束馈源 73.78 54.91 –13.50 0.0626 –0.185 –0.68 致密焦面阵列馈源 74.42 63.57 –15.30 0.0626 –0.180 –0.56 1号1.25 GHz 焦面场 76.67 75.46 –16.90 0.0500 0.000 0.00 多喇叭多波束馈源 76.18 67.29 –26.80 0.0527 0.000 0.00 致密焦面阵列馈源 76.62 74.42 –19.10 0.0514 0.000 0.00 5号1.25 GHz 焦面场 76.57 73.66 –17.10 0.0500 –0.045 –0.10 多喇叭多波束馈源 76.05 65.34 –21.50 0.0530 –0.045 –0.12 致密焦面阵列馈源 76.55 73.36 –18.40 0.0519 –0.045 –0.06 14号1.25 GHz 焦面场 76.46 71.80 –16.20 0.0502 –0.090 –0.21 多喇叭多波束馈源 75.84 62.31 –17.20 0.0542 –0.090 –0.33 致密焦面阵列馈源 76.25 68.37 –18.60 0.0529 –0.090 –0.36 29号1.25 GHz 焦面场 76.33 69.67 –16.10 0.0505 –0.140 –0.34 多喇叭多波束馈源 75.60 58.97 –15.00 0.0538 –0.140 –0.57 致密焦面阵列馈源 76.20 67.66 –19.20 0.0526 –0.135 –0.41 50号1.25 GHz 焦面场 76.13 66.50 –15.70 0.0512 –0.180 –0.54 多喇叭多波束馈源 75.29 54.86 –13.00 0.0548 –0.185 –0.88 致密焦面阵列馈源 75.97 64.17 –15.80 0.0535 –0.185 –0.64 1号1.45 GHz 焦面场 78.06 77.07 –16.70 0.0426 0.000 0.00 多喇叭多波束馈源 77.52 68.06 –30.60 0.0468 0.000 0.00 致密焦面阵列馈源 78.01 76.19 –19.90 0.0440 0.000 0.00 5号1.45 GHz 焦面场 77.97 75.49 –16.60 0.0426 –0.045 –0.09 多喇叭多波束馈源 77.39 66.05 –21.60 0.0470 –0.045 –0.13 致密焦面阵列馈源 77.90 74.28 –18.80 0.0437 –0.045 –0.11 14号1.45 GHz 焦面场 77.85 73.43 –16.20 0.0427 –0.095 –0.21 多喇叭多波束馈源 77.16 62.64 –17.20 0.0480 –0.095 –0.35 致密焦面阵列馈源 77.64 69.96 –20.10 0.0456 –0.095 –0.37 29号1.45 GHz 焦面场 77.67 70.45 –16.50 0.0488 –0.140 –0.39 多喇叭多波束馈源 76.86 58.46 –15.00 0.0486 –0.140 –0.65 致密焦面阵列馈源 77.49 67.59 –17.50 0.0445 –0.140 –0.52 50号1.45 GHz 焦面场 77.43 66.66 –16.00 0.0439 –0.185 –0.63 多喇叭多波束馈源 76.44 53.07 –12.80 0.0499 –0.185 –1.07 致密焦面阵列馈源 77.22 63.52 –13.70 0.0465 –0.180 –0.79 -
CHEN Yang, MENG Hongfu, GAN Yu, et al. Millimeter wave multi-beam reflector antenna[C]. 2018 International Workshop on Antenna Technology, Nanjing, China, 2018: 1–3. doi: 10.1109/IWAT.2018.8379140. MANOOCHEHRI O, EMADEDDIN A, DARVAZEHBAN A, et al. A new method for designing high efficiency multi feed multi beam reflector antennas[C]. 2017 International Conference on Electromagnetics in Advanced Applications, Verona, Italy, 2017: 551–554. doi: 10.1109/ICEAA.2017.8065304. ANGEVAIN J C, FONSECA N, SCHOBERT D, et al. Multibeam reflector antennas for space applications: Current trends and future perspectives in Europe[C]. The 12th European Conference on Antennas and Propagation, London, UK, 2018: 1–5. doi: 10.1049/cp.2018.0804. HE Shanhong, LI Wenkai, LU Xiaojia, et al. Predicting influence of the rest spherical surface on the instantaneous parabolic surface of multi-beam for radio astronomy[C]. 2018 IEEE MTT-S international wireless symposium, Chengdu, China, 2018: 1–3. doi: 10.1109/IEEE-IWS.2018.8400911. SMITH S L, DUNNING A, SMART K W, et al. Performance validation of the 19-element multibeam feed for the five-hundred-metre aperture spherical radio telescope[C]. 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, USA, 2017: 2137–2138. DUNNING A, BOWEN M, CASTILLO S, et al. Design and laboratory testing of the five hundred meter aperture spherical telescope (FAST) 19 beam L-band receiver[C]. The 2017 32nd General Assembly and Scientific Symposium of the International Union of Radio Science, Montreal, Canada, 2017. doi: 10.23919/URSIGASS.2017.8105012. LIU Lei and GRAINGE K. Realization of phased arrays for reflector observing systems[C]. The 2017 32nd General Assembly and Scientific Symposium of the International Union of Radio Science, Montreal, Canada, 2017. doi: 10.23919/URSIGASS.2017.8105014. HUT B, VAN DEN BRINK R H, and VAN CAPPELLEN W A. Status update on the system validation of APERTIF, the phased array feed system for the westerbork synthesis radio telescope[C]. The 2017 11th European Conference on Antennas and Propagation, Paris, France, 2017: 1960–1961. doi: 10.23919/EuCAP.2017.7928787. WU Yang, WARNICK K F, and JIN Chengjin. Design study of an L-band phased array feed for wide-field surveys and vibration compensation on FAST[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(6): 3026–3033. doi: 10.1109/TAP.2013.2254438 IVASHINA M V, KEHN M N M, KILDAL P S, et al. Control of reflection and mutual coupling losses in maximizing efficiency of dense focal plane arrays[C]. The 20061st European Conference on Antennas and Propagation, Nice, France, 2006: 1–6. doi: 10.1109/EUCAP.2006.4585045. IVASHINA M and VAN ARDENNE J D B A. A way to improve the field of view of the radiotelescope with a dense focal plane array[C]. The 12th International Conference Microwave and Telecommunication Technology, Sevastopol, Ukraine, 2002: 278–281. doi: 10.1109/CRMICO.2002.1137238. IVASHINA M and BREGMAN J. Experimental synthesis of a feed pattern with a dense focal plane array[C]. The 200232nd European Microwave Conference, Milan, Italy, 2002: 1–4. doi: 10.1109/EUMA.2002.339456. SHI Wei, ZHANG Quansheng, and DU Hui. Quantum particle swarm optimization for integer programming of phased array feeds[C]. 2010 International Conference on Microwave and Millimeter Wave Technology, Chengdu, China, 2010: 1386–1389. doi: 10.1109/ICMMT.2010.5524774. CHANG D C, HU C N, HUNG C I, et al. Pattern synthesis of the offset reflector antenna system with less complicated phased array feed[J]. IEEE Transactions on Antennas and Propagation, 1994, 42(2): 240–245. doi: 10.1109/8.277218 TANAKA S, YAMADA T, MURATA T, et al. A study on pattern synthesis method for array-fed reflector antenna for advanced direct broadcasting satellites[C]. 2001 IEEE Antennas and Propagation Society International Symposium, Boston, USA, 2001: 566–569. doi: 10.1109/APS.2001.958916. SAKA B and YAZGAN E. Pattern optimization of a reflector antenna with planar-array feeds and cluster feeds[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(1): 93–97. doi: 10.1109/8.554245 WHITE W D. Circular aperture distribution functions[J]. IEEE Transactions on Antennas and Propagation, 1977, 25(5): 714–716. doi: 10.1109/TAP.1977.1141672 SKULKIN S P, TURCHIN V I, KASCHEEV N I, et al. Transient field calculation of aperture antennas for various field distributions over the aperture[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2295–2298. doi: 10.1109/LAWP.2017.2715323 DUAN D W and RAHMAT-SAMII Y. A generalized three-parameter (3-P) aperture distribution for antenna applications[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(6): 697–713. doi: 10.1109/8.144605 IUPIKOV O A, IVASHINA M V, SKOU N, et al. Multibeam focal plane arrays with digital beamforming for high precision space-borne ocean remote sensing[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(2): 737–748. doi: 10.1109/TAP.2017.2763174 ELMER M, JEFFS B D, WARNICK K F, et al. Beamformer design methods for radio astronomical phased array feeds[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(2): 903–914. doi: 10.1109/TAP.2011.2173143 CHIPPENDALE A P, MCCONNELL D, BANNISTER K, et al. Recent developments in measuring signal and noise in phased array feeds at CSIRO[C]. The 201610th European Conference on Antennas and Propagation, Davos, Switzerland, 2016: 1–5. doi: 10.1109/EuCAP.2016.7481741. -





 下载:
下载:




 下载:
下载:
