Energy Efficiency Based Dynamic Resource Allocation Algorithm for Cellular Vehicular Based on Non-Orthogonal Multiple Access
-
摘要:
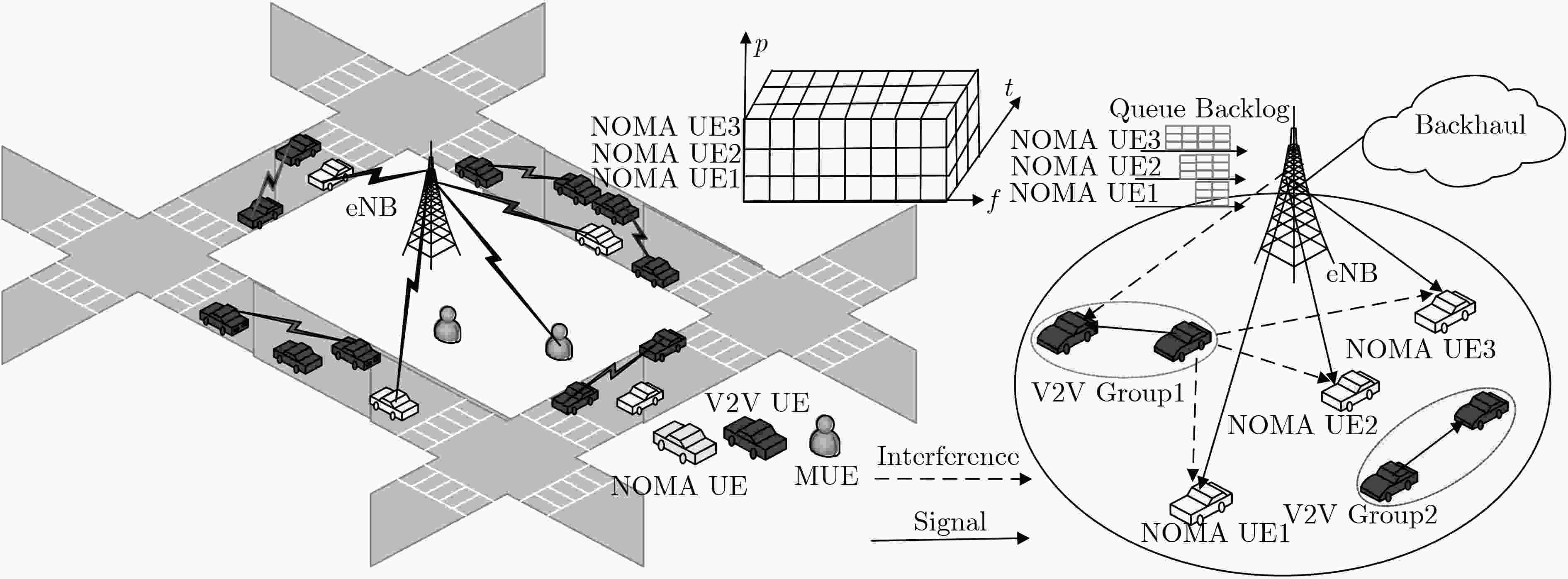
在支持车与车直接通信(V2V)的非正交多址接入(NOMA)蜂窝网络场景下,针对V2V用户与蜂窝用户的干扰以及NOMA准则下的功率分配问题,该文提出一种基于能效的动态资源分配算法。该算法首先为了保证V2V用户的时延及可靠性同时满足蜂窝用户的速率需求,联合考虑子信道调度、功率分配和拥塞控制,建立了最大化系统能效的随机优化模型。其次,利用李雅普诺夫随机优化方法,通过控制可接入数据量保证队列稳定性以避免网络拥塞,并根据实时网络负载状态动态地进行资源调度,设计一种次优化子信道匹配算法获得用户调度方案,进一步,利用凸优化理论和拉格朗日对偶分解方法得到功率分配策略。最后,仿真结果表明,该文算法可以满足不同用户的服务质量(QoS)需求,并在保证网络稳定性前提下提高系统能效。
Abstract:In the Non-Orthogonal Multiple Access (NOMA) based cellular network with Vehicle-to-Vehicle (V2V) communication, to mitigate the co-channel interference between V2V users and cellular users as well as the power allocation problem based on the NOMA principle, an energy efficiency dynamic resource allocation algorithm is proposed. Firstly, a stochastic optimization model is established to maximize the energy efficiency by considering subchannel scheduling, power allocation and congestion control, in order to guarantee the delay and reliability of V2V users while satisfying the rate of cellular users. Then, leveraging on the Lyapunov stochastic optimization method, the traffic queues can be stabilized by admitting as much traffic data as possible to avoid network congestion, and the radio resource can be allocated dynamically according to the real-time network traffic and thus a suboptimal subchannel matching algorithm is designed to obtain the user scheduling scheme. Furthermore, the power allocation policy is obtained by utilizing successive convex optimization theory and Lagrange dual decomposition method. Finally, the simulation results show that the proposed algorithm can improve the system energy efficiency and ensure the Quality of Service (QoS) requirements of different users and network stability.
-
表 1 基于能效的动态资源分配算法
(1) 初始化控制参数$V$, NOMA用户队列${Q_i}(0) = 0$、虚拟队列${Q_k}(0) = 0$、${H_i}(0) = 0$, ${\varGamma _i}(t)$, $R_k^{\min }$, $\forall k \in K,i \in I$; (2) 设置时隙长度${T_{\max }}$; (3) For $t = 0,1, ··· ,{T_{\max }} - 1,$ do; (4) 观察该时隙每个NOMA用户的队列状态${Q_i}(t)$以及虚拟队列${Q_k}(t)$和${H_i}(t)$; (5) 计算辅助变量${\gamma _i}(t)$,然后根据式(18)和式(19)得到拥塞控制优化解$\varGamma _i^*$; (6) 执行表2求解优化问题式(16)得到子信道调度策略$x_i^*,\alpha _k^*$; (7) 执行表3求解问题式(21)得到优化的功率分配方案$\{ p_1^{\rm{*}},p_2^{\rm{*}},···,p_{M{\rm{ - }}1}^{\rm{*}}\} $; (8) 根据下面公式分别更新下一时隙NOMA用户的队列状态${Q_i}(t + 1)$,虚拟队列状态${Q_k}(t + 1)$和${H_i}(t + 1)$;
${Q_i}(t + 1) = \max \{ {Q_i}(t) + {\varGamma _i}(t) - {r_i}(t),0\} ,\;\;\forall i$, ${Q_k}(t + 1) = \max \{ {Q_k}(t) + R_k^{\min } - {r_k}(t),0\} ,\forall k$;
${H_i}(t + 1) = \max \{ {H_i}(t) - {\varGamma _i}(t) + {\gamma _i}(t),0\} ,\forall i$;(9) $t = t + 1$; (10) End; (11) 输出优化拥塞控制策略、频谱和功率分配方案$\varGamma _i^*$, $x_i^*,\alpha _k^*$, $p_i^*,p_k^*$。 表 2 联合次优化子信道匹配算法
(1) 初始化${p_i},{p_k}$, ${Q_i}(0) = 0$, ${Q_k}(0) = 0$, ${H_i}(0) = 0$,初始化未分配子信道的NOMA和V2V用户集$S_{{\rm{un}}}^C$, $S_{{\rm{un}}}^V$,复用同一信道的用户集
${{U}} = \{ U_1,U_2,···,U_N\} $, ${\psi _n} = \varnothing $,用户调度策略${{x}} = \varnothing ,{{\alpha}} = \varnothing $,分别构造NOMA用户和V2V用户的信道增益矩阵,${{ H}_i} \triangleq {[|{h_{i,n}}|]_{I \times N}}$,
${{ H}_k} \triangleq {[|{h_{k,n}}|]_{K \times N}}$;(2) while ${S_{{\rm{un}}}}^C \ne \varnothing $&${S_{\rm{un}}}^V \ne \varnothing$ do; (3) for $n = 1:N$; (4) 从${{ H}_i}$中找到最大信道增益,将子信道$n$调度给用户$i$,更新${{x}}$,并将矩阵中的第$i$行元素置0; (5) 更新${U_n} = {U_n} \cup u_n^i$ & $S_{{\rm{un}}}^C = S_{{\rm{un}}}^C\backslash u_n^i$; (6) end for; (7) for $n = 1:N$; (8) while ${N_{{U_n}}} < M$ do; (9) 分别从信道矩阵${{ H}_i}$和${{ H}_k}$ 中找到最大信道增益$|{h_{i,n}}|$和$|{h_{k,n}}|$; (10) if ${\rm{|}}{h_{i,n}}| > {h_{k,n}}|$; (11) 将子信道$n$分配给用户$i$,更新${U_n} = {U_n} \cup u_i^n$; (12) else; (13) 将子信道$n$分配给用户$k$,更新${U_n} = {U_n} \cup u_k^n$; (14) end if; (15) end while; (16) if ${N_{{U_n}}} = M$; (17) 计算用户集${U_n}$复用在子信道$n$上的$\varphi (t)$,并将结果保存于${\psi _n}$ (18) 求解式(16)得到用户调度的解$x_i^n,\alpha _k^n$以及被调度用户集$u_n^C,u_n^V$,更新未调度用户集$S_{un}^C = S_{un}^C\backslash u_n^C$ & $S_{un}^V = S_{un}^V\backslash u_n^V$,并将
信道矩阵${{ H}_i}$中的第$i$行置0,或将${{ H}_k}$中的第$k$行元素及第$n$列元素置0;(19) end if; (20) end for; (21) end while; (22) 输出用户调度策略${{x}},{{\alpha}} $。 表 3 基于连续凸逼近和拉格朗日对偶的迭代功率优化算法
(1) 初始化最大迭代次数${T_1}$及最大允许误差${\xi _1}$,初始化${[{\tilde p_i}(t),{\tilde p_k}(t)]^0}$,迭代次数索引$t$; (2) while $g \le {T_1}$ or ${\rm{||}}\tilde \varphi ({[{\tilde p_i}(t),{\tilde p_k}(t)]^g}) - \tilde \varphi ({[{\tilde p_i}(t),{\tilde p_k}(t)]^{g - 1}})|| \le {\xi _1}$ do; (3) 根据迭代得到的${[{\tilde p_i}(t),{\tilde p_k}(t)]^g}$和$\tilde r_k^n$, $\tilde r_i^n$计算$c_k^n$ $d_k^n$ $c_i^n$ $d_i^n$,得到更新后的${{{c}}^g},{{{d}}^g}$; (4) 求解优化问题式(20),更新当前最优解${[{\tilde p_i}(t),{\tilde p_k}(t)]^{{\rm{g + 1}}}}$并令$g = g + 1$; (5) end while; (6) 输出连续凸逼近迭代后的优化解$\tilde P(t) = {\left[ {{{\tilde p}_i}(t),\tilde p{}_k(t)} \right]^g}$; (7) 初始化最大迭代次数${N_1}$和${N_2}$及收敛条件${\varDelta _1}$和${\varDelta _2}$,初始化迭代索引$m = 0,n = 0$,初始化拉格朗日乘子${\nu ^0},{\lambda ^0},{\mu ^0},{\eta ^0}$,
${[{\tilde p_i}{(t)_m},\tilde p{}_k{(t)_m}]^0} = {[{\tilde p_i}{(t)_n},{\tilde p_k}{(t)_n}]^0} = {[{\tilde p_i}(t),{\tilde p_k}(t)]^g}$;(8) 观察时隙$t$每个NOMA用户的队列状态${Q_i}(t)$和虚拟队列状态${Q_k}(t)$, ${H_i}(t)$; (9) while $m < {N_1}$ or ${\rm{||} }\tilde \varphi ({[{\tilde p_i}{(t)_m},{\tilde p_k}{(t)_m}]^{m + 1} }) - \tilde \varphi ({[{\tilde p_i}{(t)_m},{\tilde p_k}{(t)_m}]^m})|| \ge {\varDelta _1}$ do; (10) while $n < {N_2}$ or $||{J^{n + 1} }(t) - {J^n}(t)|| \ge {\varDelta _2}$ do; (11) 将${\nu ^m},{\lambda ^m},{\mu ^m},{\eta ^m}$和${[{\tilde p_i}{(t)_n},{\tilde p_k}{(t)_n}]^n}$分别代入表达式(21)求导; (12) 通过KKT条件和二分搜索法求得功率分配${[{\tilde p_i}{(t)_n},{\tilde p_k}{(t)_n}]^{n + 1}}$,更新拉格朗日乘子; (13) $n = n + 1$; (14) end while; (15) $m = m + 1$; (16) end while; -
3GPP. Study on LTE-based V2X services 14.0.0[R]. 3GPP TR 36.885, 2016. 3GPP. Study on enhancement of 3GPP support for 5G V2X services 16.2.0[R]. 3GPP TR 22.886, 2017. SAHIN T, KLUGEL M, ZHOU Chan, et al. Virtual cells for 5G V2X communications[J]. IEEE Communications Standards Magazine, 2018, 2(1): 22–28. doi: 10.1109/MCOMSTD.2018.1700060 YANG Zhaohui, XU Wei, PAN Cunhua, et al. On the optimality of power allocation for NOMA downlinks with individual QoS constraints[J]. IEEE Communications Letters, 2017, 21(7): 1649–1652. doi: 10.1109/LCOMM.2017.2689763 PAN Yijin, PAN Cunhua, YANG Zhaohui, et al. Resource allocation for D2D communications underlaying a NOMA-based cellular network[J]. IEEE Wireless Communications Letters, 2018, 7(1): 130–133. doi: 10.1109/LWC.2017.2759114 LIANG Le, LI G Y, and XU Wei. Resource allocation for D2D-enabled vehicular communications[J]. IEEE Transactions on Communications, 2017, 65(7): 3186–3197. doi: 10.1109/TCOMM.2017.2699194 LIU Chenfeng and BENNIS M. Ultra-reliable and low-latency vehicular transmission: An extreme value theory approach[J]. IEEE Communications Letters, 2018, 22(6): 1292–1295. doi: 10.1109/LCOMM.2018.2828407 SUN Wanlu, STRÖM E, BRÄNNSTRÖM F, et al. Radio resource management for D2D-based V2V communication[J]. IEEE Transactions on Vehicular Technology, 2016, 65(8): 6636–6650. doi: 10.1109/TVT.2015.2479248 SUN Wanlu, STRÖM E, BRÄNNSTRÖM F, et al. D2D-based V2V communications with latency and reliability constraints[C]. 2014 IEEE Globecom Workshops, Austin, USA, 2014: 1414–1419. doi: 10.1109/GLOCOMW.2014.7063632. PENG Mugen, YU Yuling, XIANG Hongyu, et al. Energy-efficient resource allocation optimization for multimedia heterogeneous cloud radio access networks[J]. IEEE Transactions on Multimedia, 2016, 18(5): 879–892. doi: 10.1109/TMM.2016.2535722 LAU V K N, ZHANG Fan, and CUI Ying. Low complexity delay-constrained beamforming for multi-user MIMO systems with imperfect CSIT[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 4090–4099. doi: 10.1109/TSP.2013.2264058 CHUNG S T and GOLDSMITH A J. Degrees of freedom in adaptive modulation: A unified view[J]. IEEE Transactions on Communications, 2001, 49(9): 1561–1571. doi: 10.1109/26.950343 LI Jian, PENG Mugen, YU Yuling, et al. Energy-efficient joint congestion control and resource optimization in heterogeneous cloud radio access networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(12): 9873–9887. doi: 10.1109/TVT.2016.2531184 ZHAO Long and WANG Xiaodong. Round-trip energy efficiency of wireless energy powered massive MIMO system with latency constraint[J]. IEEE Communications Letters, 2017, 21(1): 12–15. doi: 10.1109/LCOMM.2016.2616858 KHAN Z, FAN Pingzhi, ABBAS F, et al. Two-level cluster based routing scheme for 5G V2X communication[J]. IEEE Access, 2019, 7: 16194–16205. doi: 10.1109/ACCESS.2019.2892180 ZHANG Yi, WANG Huiming, ZHENG Tongxing, et al. Energy-efficient transmission design in non-orthogonal multiple access[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 2852–2857. doi: 10.1109/TVT.2016.2578949 -





 下载:
下载:




 下载:
下载:
