Sparse Reconstruction OFDM Delay Estimation Algorithm Based on Bayesian Automatic Relevance Determination
-
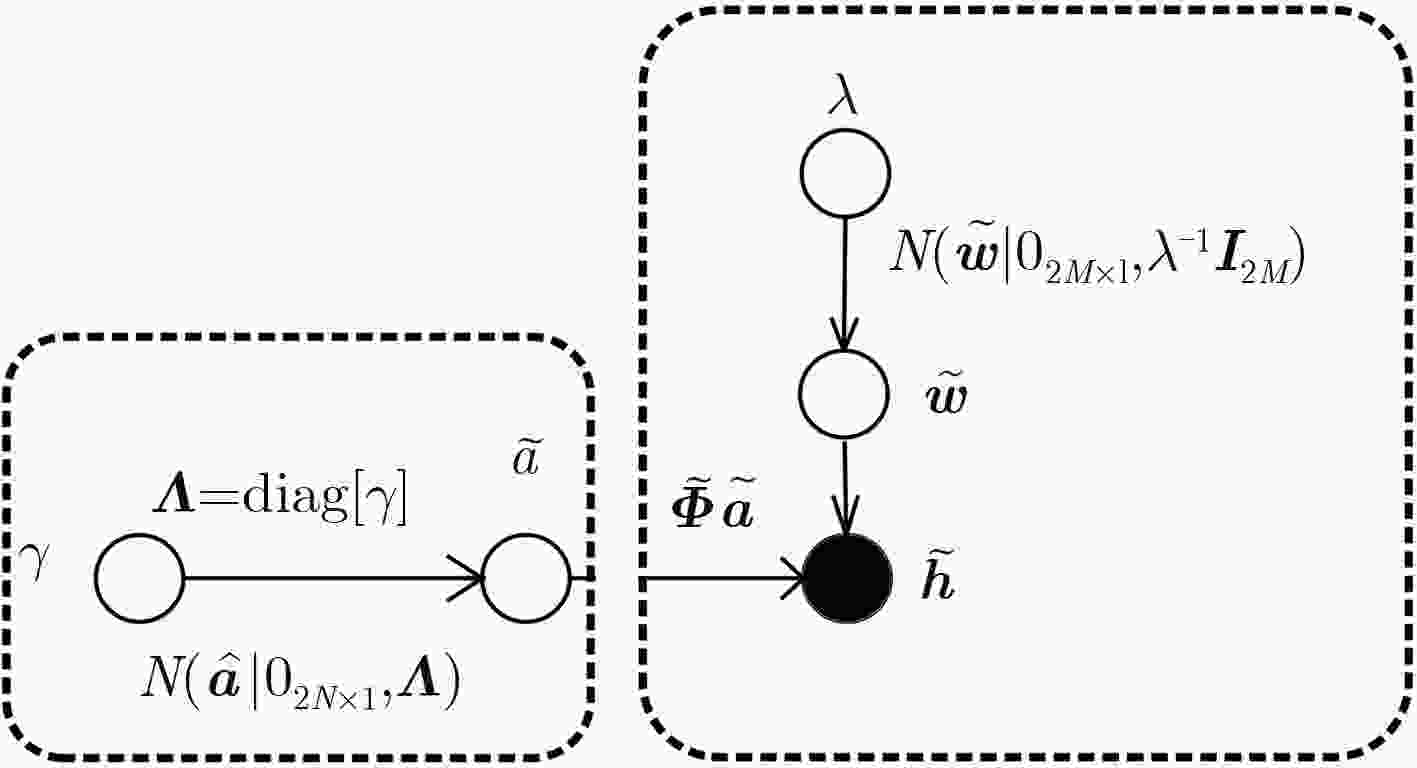
摘要: 针对复杂环境下,单测量矢量(SMV)条件下的正交频分复用(OFDM)时延估计问题,该文提出了一种基于贝叶斯自动相关性确定(BARD)的稀疏重构时延估计算法。该算法运用贝叶斯框架,从进一步挖掘有用信息的角度入手,引入不对称的自动相关性确定(ARD)先验,融入参数估计过程中,有效提升了低信噪比(SNR)和SMV条件下的时延估计精度。该算法首先基于OFDM信号物理层协议数据单元估计出的信道频域响应构造稀疏化实数域表示模型,然后对模型中的噪声和稀疏系数矢量进行概率假设,同时引入自动相关性确定先验;最后根据贝叶斯框架,通过期望最大化(EM)算法求解超参数,实现对时延的估计。仿真实验表明,该算法具有更好的估计性能,在信噪比较高时更加贴近克拉美罗界(CRB)。同时基于通用软件无线电外设(USRP),利用实际信号对所提算法进行了有效性地验证。
-
关键词:
- 时延估计 /
- 神经网络 /
- 自动相关性确定(ARD) /
- 通用软件无线电外设(USRP)
Abstract: Considering the problem of Orthogonal Frequency Division Multiplexing (OFDM) signal delay estimation with only a Single Measurement Vector (SMV) in a complex environment, a sparse reconstruction time delay estimation algorithm based on Bayesian Automatic Relevance Determination (BARD) is proposed. The Bayesian framework is used to start from the perspective of further mining useful information, and asymmetric Automatic Relevance Determination(ARD) priori is introduced to integrate into the parameter estimation process, which improves the accuracy of time delay estimation under SMV and low Signal-to-Noise Ratio (SNR) conditions. Firstly, a sparse real-domain representation model is constructed based on the estimated frequency domain response of the OFDM signal physical layer protocol data unit. Then, probability hypothesis for the noise and sparse coefficient vectors are made in the model, and Automatic Relevance Determination (ARD) prior is introduced. Finally, according to the Bayesian framework, the Expectation Maximization (EM) algorithm is used to solve the hyperparameters to estimate the delay. The simulation experiments show that the proposed algorithm has better estimation performance and is closer to the Cramér–Rao Bound (CRB). At the same time, based on the Universal Software Radio Peripheral (USRP), the effectiveness of the proposed algorithm is verified by the actual signal. -
表 1 OFDM系统参数设置
参数 数值 FFT周期${T_{{\rm{FFT}}}}(\mu s)$ 3.2 系统带宽$B({\rm{MHz}})$ 20 子载波数(个) 64 载波频率${f_{\rm{c}}}{\rm{(GHz}})$ 2.4 表 2 各种算法时延估计结果比较(ns)
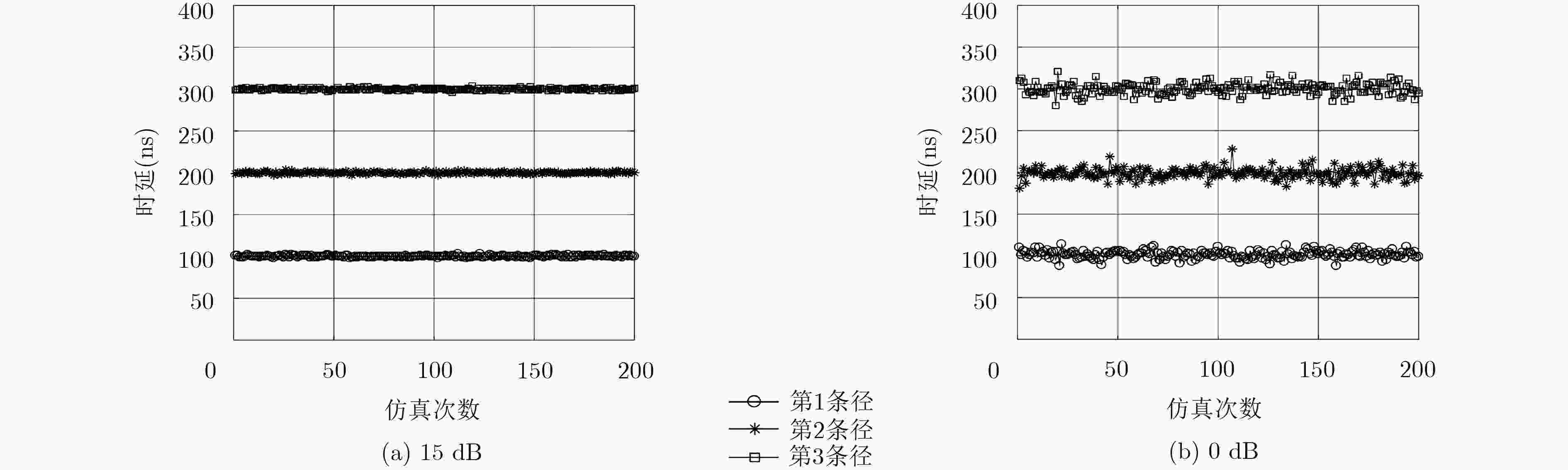
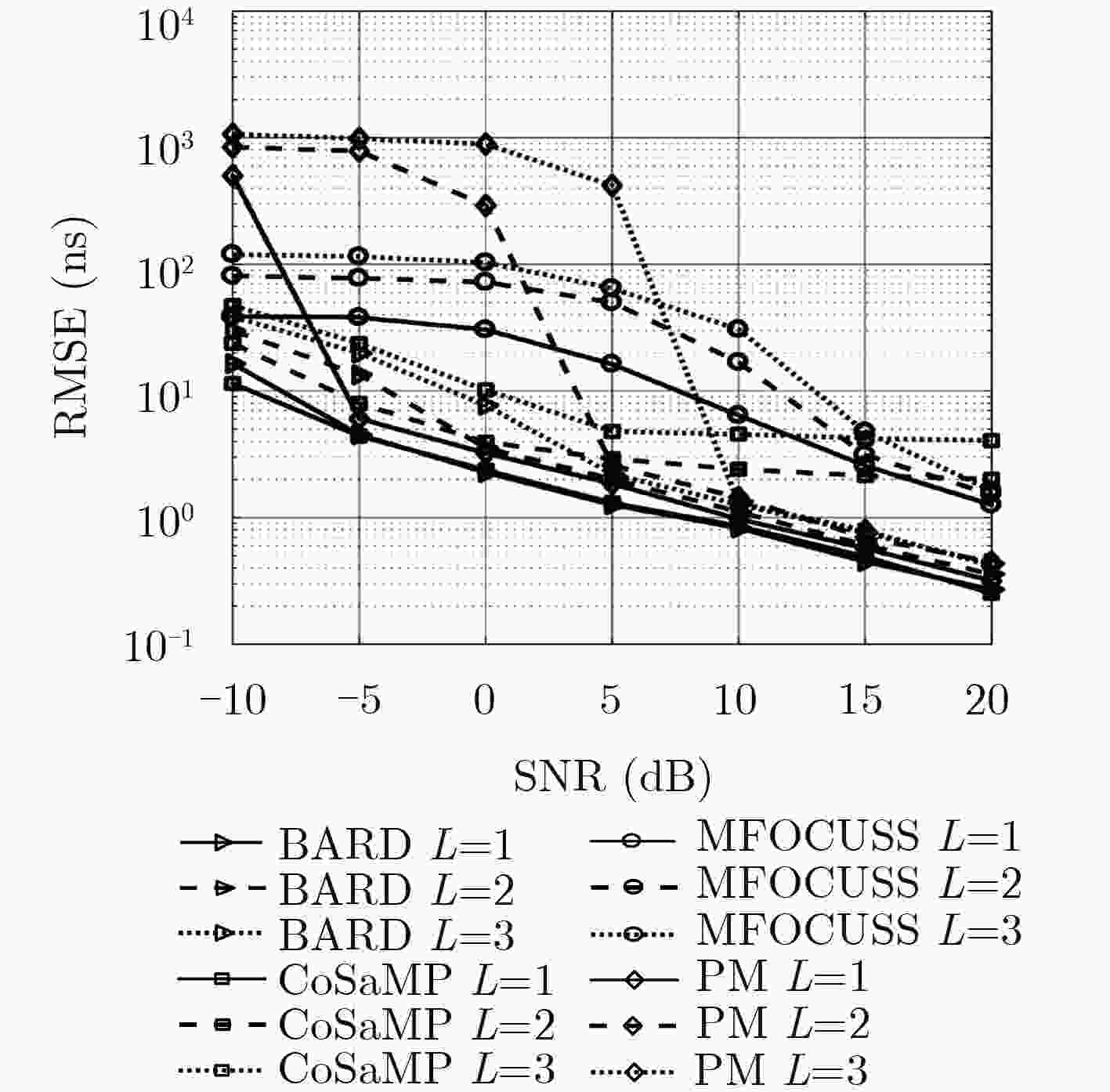
算法 多径序号 1 2 3 4 均值 RMSE 均值 均值 均值 PM 218.40 10.81 270.93 302.16 308.16 CoSaMP 211.00 10.57 262.33 287.50 298.06 MFOCUSS 204.16 4.50 258.16 287.66 307.20 BARD 201.53 1.17 253.00 283.00 314.32 -
VAN NEE R and PRASAD R. OFDM for Wireless Multimedia Communications[M]. Boston: Artech House, 2000: 3–4. SEGURA M J, MUT V A, and PATIÑO H D. Mobile robot self-localization system using IR-UWB sensor in indoor environments[C]. 2009 IEEE International Workshop on Robotic and Sensors Environments, Lecco, Italy, 2009: 29–34. CHAN Y T, HANG H Y C, and CHING P C. Exact and approximate maximum likelihood localization algorithms[J]. IEEE Transactions on Vehicular Technology, 2006, 55(1): 10–16. doi: 10.1109/TVT.2005.861162 CELEBI H and ARSLAN H. Adaptive positioning systems for cognitive radios[C]. 2007 IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Dublin, Ireland, 2007: 78–84. LIU Ying and WANG Shuxun. TOA estimation method using fourth order cumulants[C]. 2000 International Conference on Signal Processing. 16th World Computer Congress 2000, Beijing, China, 2000: 210–214. 巴斌, 刘国春, 李韬, 等. 基于哈达玛积扩展子空间的到达时间和波达方向联合估计[J]. 物理学报, 2015, 64(7): 078403. doi: 10.7498/aps.64.078403BA Bin, LIU Guochun, LI Tao, et al. Joint for time of arrival and direction of arrival estimation algorithm based on the subspace of extended hadamard product[J]. Acta Physica Sinica, 2015, 64(7): 078403. doi: 10.7498/aps.64.078403 BIALER O, RAPHAELI D, and WEISS A J. Robust time-of-arrival estimation in multipath channels with OFDM signals[C]. 2017 Signal Processing Conference, Kos, Greece, 2017: 2724–2728. CHEN Yajun, PENG Jianhua, HUANG Kaizhi, et al. A multipath delay estimation model and algorithm in OFDM systems[C]. 2014 IEEE International Conference on Information Science and Technology, Shenzhen, China, 2014: 144–147. 巴斌, 郑娜娥, 胡捍英, 等. OFDM系统中基于PM的时延估计算法[J]. 太赫兹科学与电子信息学报, 2016, 14(3): 355–360. doi: 10.11805/TKYDA201603.0355BA Bin, ZHENG Nae, HU Hanying, et al. Time delay estimation based on PM in OFDM system[J]. Journal of Terahertz Science and Electronic Information Technology, 2016, 14(3): 355–360. doi: 10.11805/TKYDA201603.0355 LI Xinrong and PAHLAVAN K. Super-resolution TOA estimation with diversity for indoor geolocation[J]. IEEE Transactions on Wireless Communications, 2004, 3(1): 224–234. doi: 10.1109/TWC.2003.819035 HÄCKER P and YANG B. Single snapshot DOA estimation[J]. Advances in Radio Science, 2010, 8: 251–256. doi: 10.5194/ars-8-251-2010 李晶, 赵拥军, 李冬海. 基于马尔科夫链蒙特卡罗的时延估计算法[J]. 物理学报, 2014, 63(13): 130701. doi: 10.7498/aps.63.130701LI Jing, ZHAO Yongjun, and LI Donghai. Time delay estimation using Markov Chain Monte Carlo method[J]. Acta Physica Sinica, 2014, 63(13): 130701. doi: 10.7498/aps.63.130701 冷雪冬, 巴斌, 逯志宇, 等. 基于回溯筛选的稀疏重构时延估计算法[J]. 物理学报, 2016, 65(21): 210701. doi: 10.7498/aps.65.210701LENG Xuedong, BA Bin, LU Zhiyu, et al. Sparse reconstruction time delay estimation algorithm based on backtracking filter[J]. Acta Physica Sinica, 2016, 65(21): 210701. doi: 10.7498/aps.65.210701 COTTER S F, RAO B D, ENGAN K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2477–2488. doi: 10.1109/TSP.2005.849172 尹艳玲, 乔钢, 刘凇佐, 等. 基于基追踪去噪的水声正交频分复用稀疏信道估计[J]. 物理学报, 2015, 64(6): 064301. doi: 10.7498/aps.64.064301YIN Yanling, QIAO Gang, LIU Songzuo, et al. Sparse channel estimation of underwater acoustic orthogonal frequency division Multiplexing based on basis pursuit denoising[J]. Acta Physica Sinica, 2015, 64(6): 064301. doi: 10.7498/aps.64.064301 NEAL R M. Bayesian Learning for Neural Networks[M]. New York: Springer-Verlag, 1996: 112–114. WIPF D and NAGARAJAN S. A new view of automatic relevance determination[C]. The 20th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2007: 1625–1632. GAST M S, O’Reilly Taiwan公司, 译. 802.11无线网络权威指南[M]. 2版. 南京: 东南大学出版社, 2007: 293–297.GAST M S, O’Reilly Taiwan, translation. 802.11 Wireless Netwoeks: The Definitive Guide[M]. 2nd ed. Nanjing: Southeast University Press, 2007: 293–297. KIM J M, LEE O K, and YE J C. Compressive MUSIC: Revisiting the link between compressive sensing and array signal processing[J]. IEEE Transactions on Information Theory, 2012, 58(1): 278–301. doi: 10.1109/TIT.2011.2171529 -





 下载:
下载:




 下载:
下载:
