Analysis of Beam Wave Interaction in a Planar Metallic Grating Based on Cyclotron Resonance Enhancement Effect
-
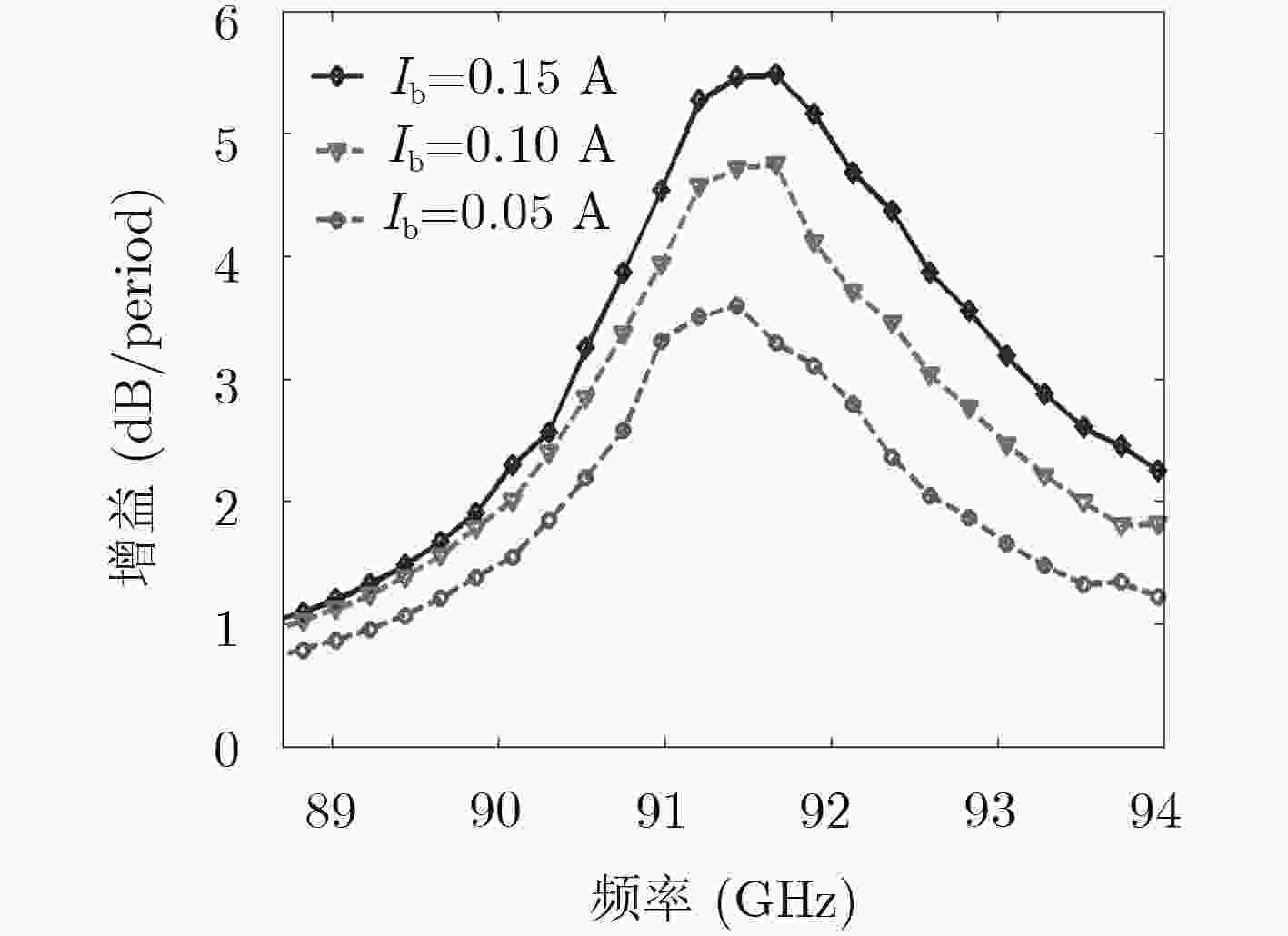
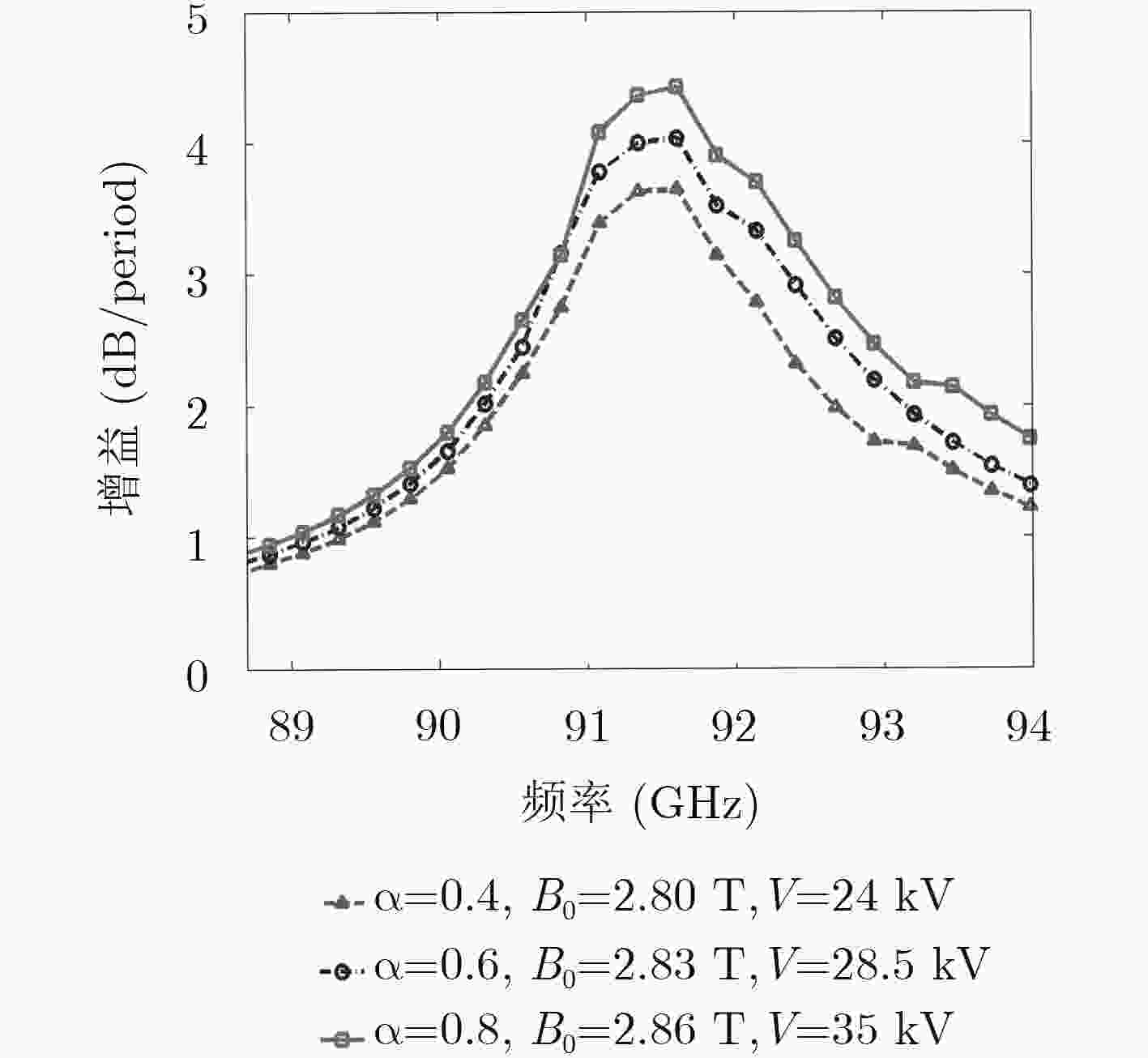
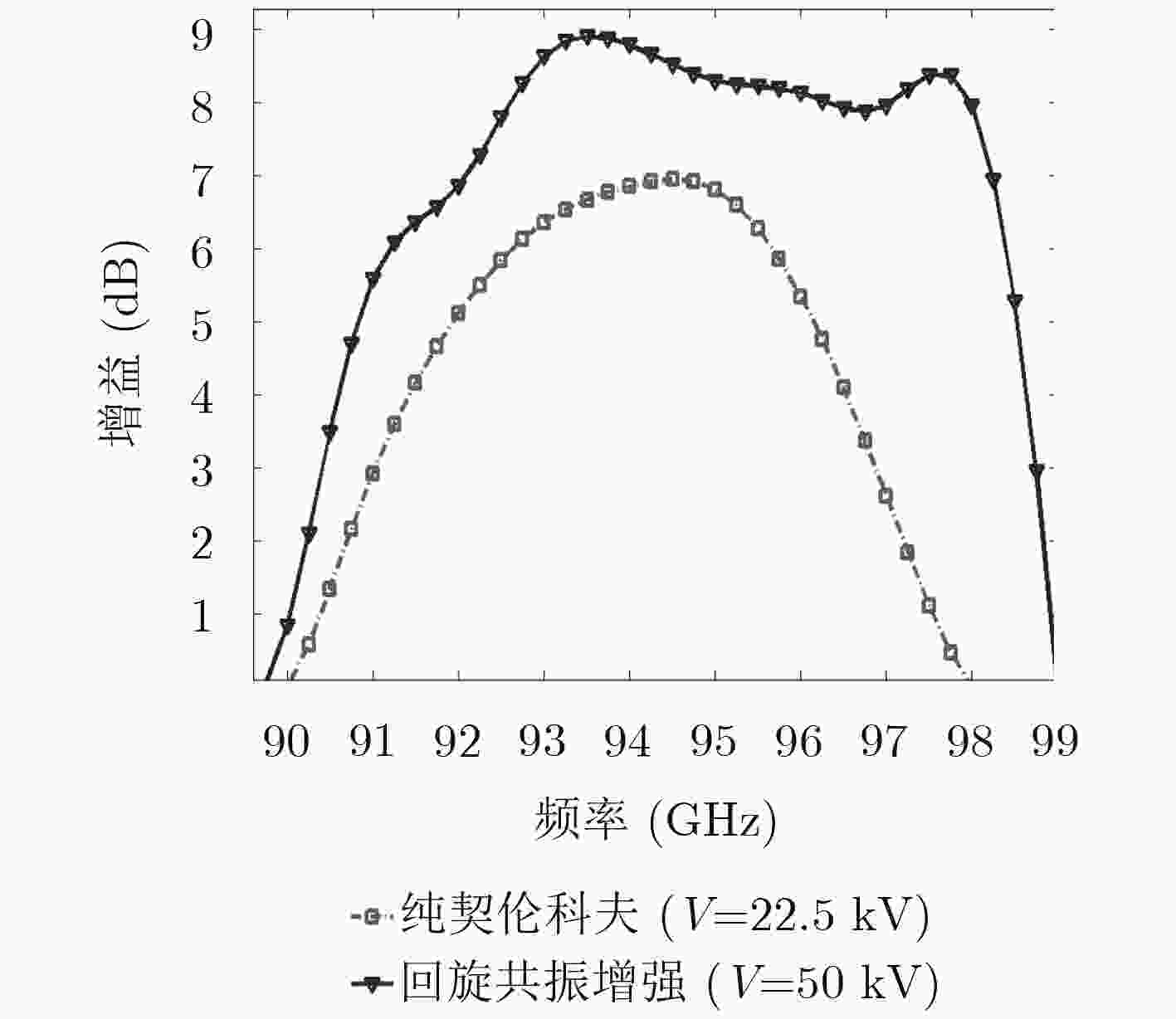
摘要: 基于电子注纵横运动与电磁场纵横分量同时同步相互作用,该文从麦克斯韦方程和线性伏拉索夫方程出发,推导出将回旋共振和契伦科夫共振同时考虑在内的平面单栅注波互作用热色散方程。在合理选择几何参数和电参数的基础上,通过热色散方程数值计算和分析,发现具有回旋共振增强效应下的注波互作用增益和频带都高于只有契伦科夫共振辐射下的结果。Abstract: Based on the beam wave synchronization interaction in transverse and longitudinal directions at the same time and derived from Maxwell’s equation and linear Vlasov equation, the planar metallic grating beam-wave interaction " hot” dispersion equation considering both cyclotron resonance and Cherenkov resonance is deduced. Through the reasonable selection for geometric and electrical parameters, the numerical calculation and analysis of the " hot” dispersion equation show that the beam-wave interaction gain and frequency band with the cyclotron resonance enhancement effect are higher than those with only Cherenkov resonance radiation.
-
Key words:
- Cyclotron /
- Cyclotron resonance enhancement /
- Planer metallic grating /
- Cherenkov effects /
- Gain
-
表 1 矩形单栅结构尺寸表(mm)
参数 几何尺寸 周期p 1.10 槽深h 1.00 栅宽a 1.75 电子注到栅顶距离${y_c}$ 0.15 栅顶边界到波导顶距离g 0.30 -
CHIPENGO U, NAHAR N K, and VOLAKIS J L. A study of velocity-tapered slow wave structures for high-efficiency backward wave oscillators[J]. IEEE Transactions on Electron Devices, 2018, 65(7): 3054–3060. doi: 10.1109/TED.2017.2769676 SAN M T, OGURA K, KUBOTA K, et al. Study on operation of oversized backward wave oscillator for broadband terahertz radiation[J]. IEEE Transactions on Plasma Science, 2018, 46(3): 530–538. doi: 10.1109/TPS.2018.2796559 PONOMARENKO S S, KISHKO S A, ZAVERTANNIY V V, et al. 400-GHz continuous-wave Clinotron oscillator[J]. IEEE Transactions on Plasma Science, 2013, 41(1): 82–86. doi: 10.1109/tps.2012.2226247 XU Changpeng, YIN Yong, BI Liangjie, et al. A novel wire-wrap slow-wave structure for Terahertz backward wave oscillator Applications[J]. IEEE Transactions on Electron Devices, 2017, 64(1): 293–299. doi: 10.1109/TED.2016.2628045 KARETNIKOVA T A, ROZHNEV A G, RYSKIN N M, et al. Gain analysis of a 0.2-THz traveling-wave tube with sheet electron beam and staggered grating slow wave structure[J]. IEEE Transactions on Electron Devices, 2018, 65(6): 2129–2134. doi: 10.1109/TED.2017.2787960 RYSKIN N M, ROZHNEV A G, STARODUBOV A V, et al. Planar microstrip slow-wave structure for low-voltage V-band traveling-wave tube with a sheet electron beam[J]. IEEE Electron Device Letters, 2018, 39(5): 757–760. doi: 10.1109/LED.2018.2821770 MINEO M and PAOLONI C. Comparison of THz backward wave oscillators based on corrugated waveguides[J]. Progress in Electromagnetics Research Letters, 2012, 30: 163–171. doi: 10.2528/PIERL12013107 MINEO M and PAOLONI C. Corrugated rectangular waveguide tunable backward wave oscillator for terahertz applications[J]. IEEE Transactions on Electron Devices, 2010, 57(6): 1481–1484. doi: 10.1109/TED.2010.2045678 MINEO M and PAOLONI C. Double-corrugated rectangular waveguide slow-wave structure for Terahertz vacuum devices[J]. IEEE Transactions on Electron Devices, 2010, 57(11): 3169–3175. doi: 10.1109/ted.2010.2071876 NUSINOVICH G S and ZHAO Ding. Combined resonances in cyclotron masers with periodic slow-wave structures[J]. IEEE Transactions on Plasma Science, 2015, 43(3): 804–814. doi: 10.1109/TPS.2015.2396354 LUCE T C. Applications of high-power millimeter waves in fusion energy research[J]. IEEE Transactions on Plasma Science, 2002, 30(3): 734–754. doi: 10.1109/TPS.2002.802147 KALARIA P C, KARTIKEYAN M V, and THUMM M. Design of 170 GHz, 1.5-MW conventional cavity Gyrotron for plasma heating[J]. IEEE Transactions on Plasma Science, 2014, 42(6): 1522–1528. doi: 10.1109/TPS.2014.2305251 THUMM M. High power Gyro-devices for plasma heating and other applications[J]. International Journal of Infrared and Millimeter Waves, 2005, 26(4): 483–503. doi: 10.1007/s10762-005-4068-8 CHU K R. The electron cyclotron maser[J]. Reviews of Modern Physics, 2004, 76(2): 489–540. doi: 10.1103/RevModPhys.76.489 ROSTOV V V, GUNIN A V, TSYGANKOV R V, et al. Two-wave Cherenkov oscillator with moderately oversized slow-wave structure[J]. IEEE Transactions on Plasma Science, 2018, 46(1): 33–42. doi: 10.1109/TPS.2017.2773661 ZHANG Keqian and LI Dejie. Electromagnetic Theory for Microwaves and Optoelectronics[M]. New York: Springer, 1998: 383–397. ZHAO Ding. Kinetic analysis of two dimensional metallic grating Cerenkov maser[J]. Physics of Plasmas, 2011, 18(8): 084508. doi: 10.1063/1.3627146 谢文球. 平面格栅慢波结构高频特性及注波互作用的研究[D]. [博士论文], 中国科学院大学, 2016.XIE Wenqiu. Investigation of the high frequency characteristics and beam wave interaction for the planar grating slow wave structure[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2016. KOU C S, WANG Q S, MCDERMOTT D B, et al. High-power harmonic gyro-TWT’s. I. Linear theory and oscillation study[J]. IEEE Transactions on Plasma Science, 1992, 20(3): 155–162. doi: 10.1109/27.142815 刘盛纲. 相对论电子学[M]. 北京: 科学出版社, 1987: 228–233.LIU Shenggang. Relativistic Electronics[M]. Beijing: Science Press, 1987: 228–233. -





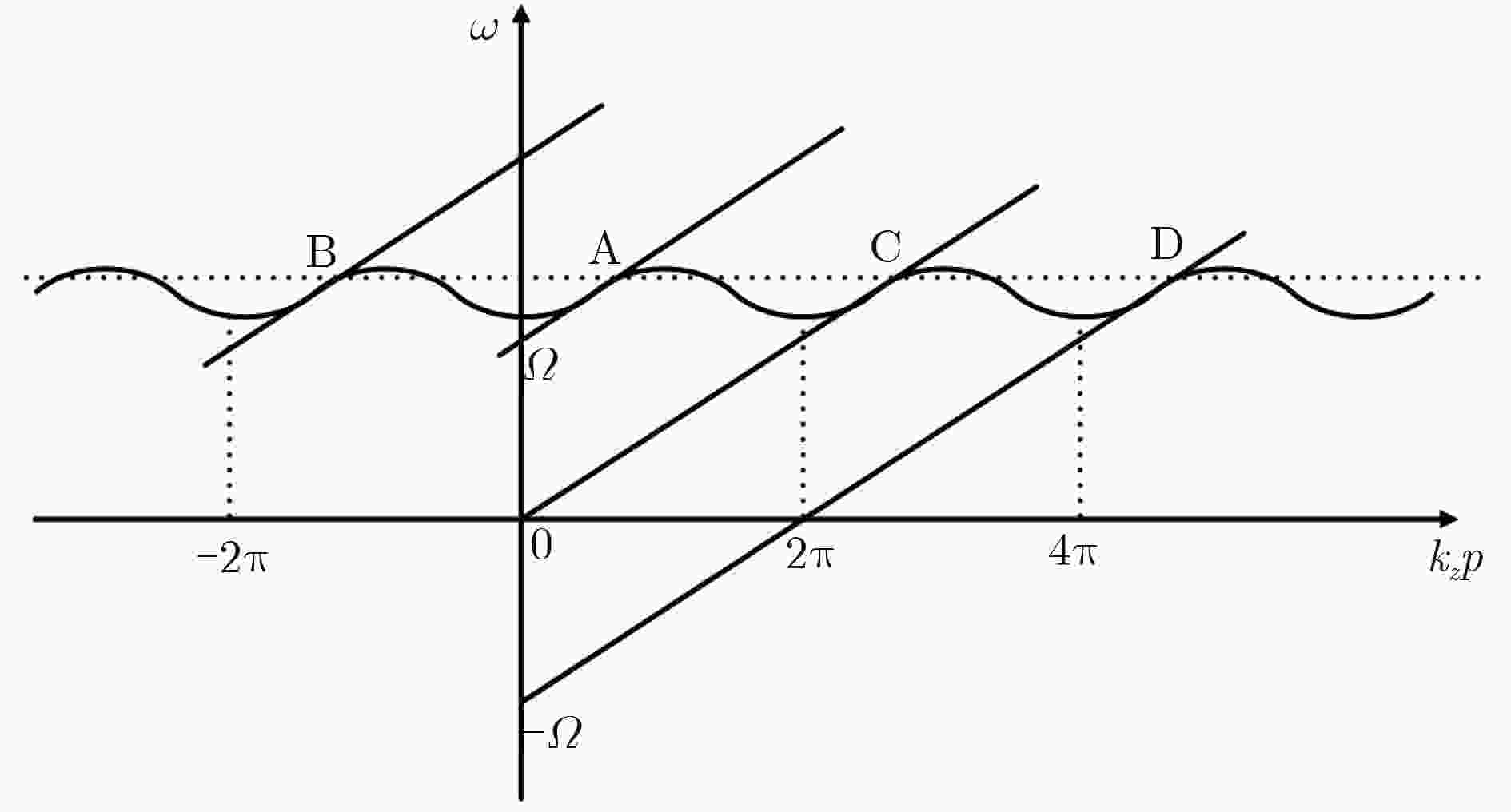
 下载:
下载:
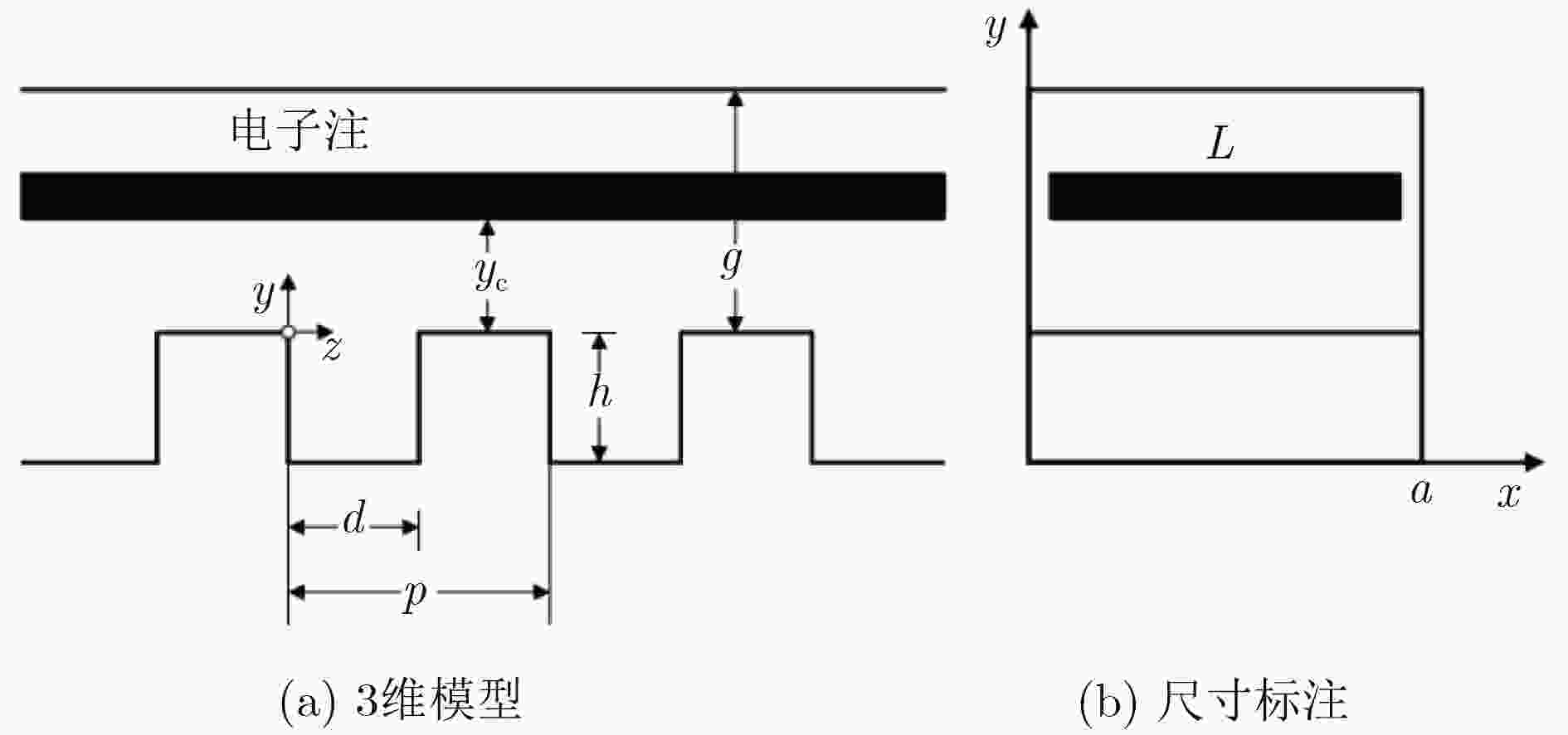
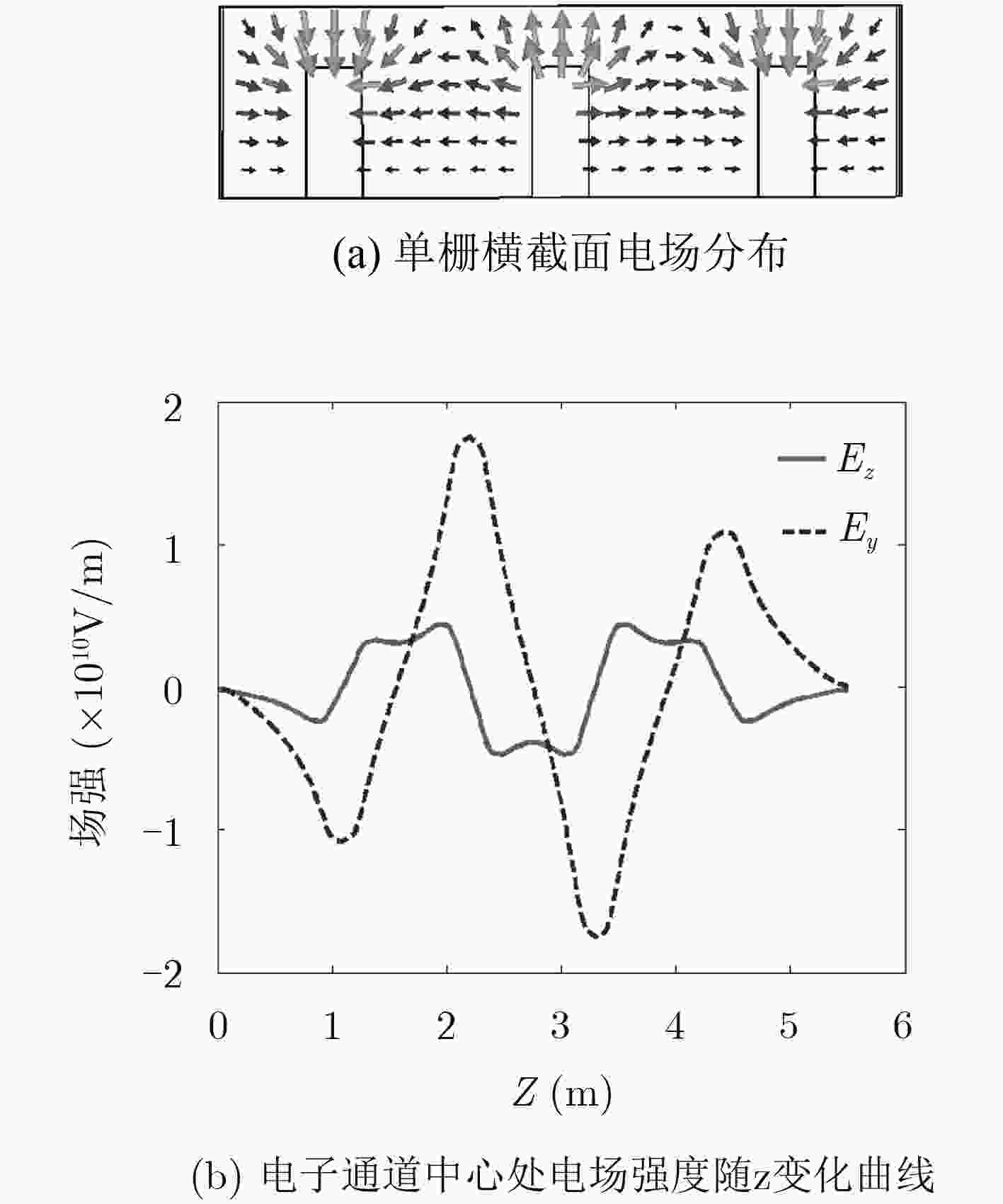
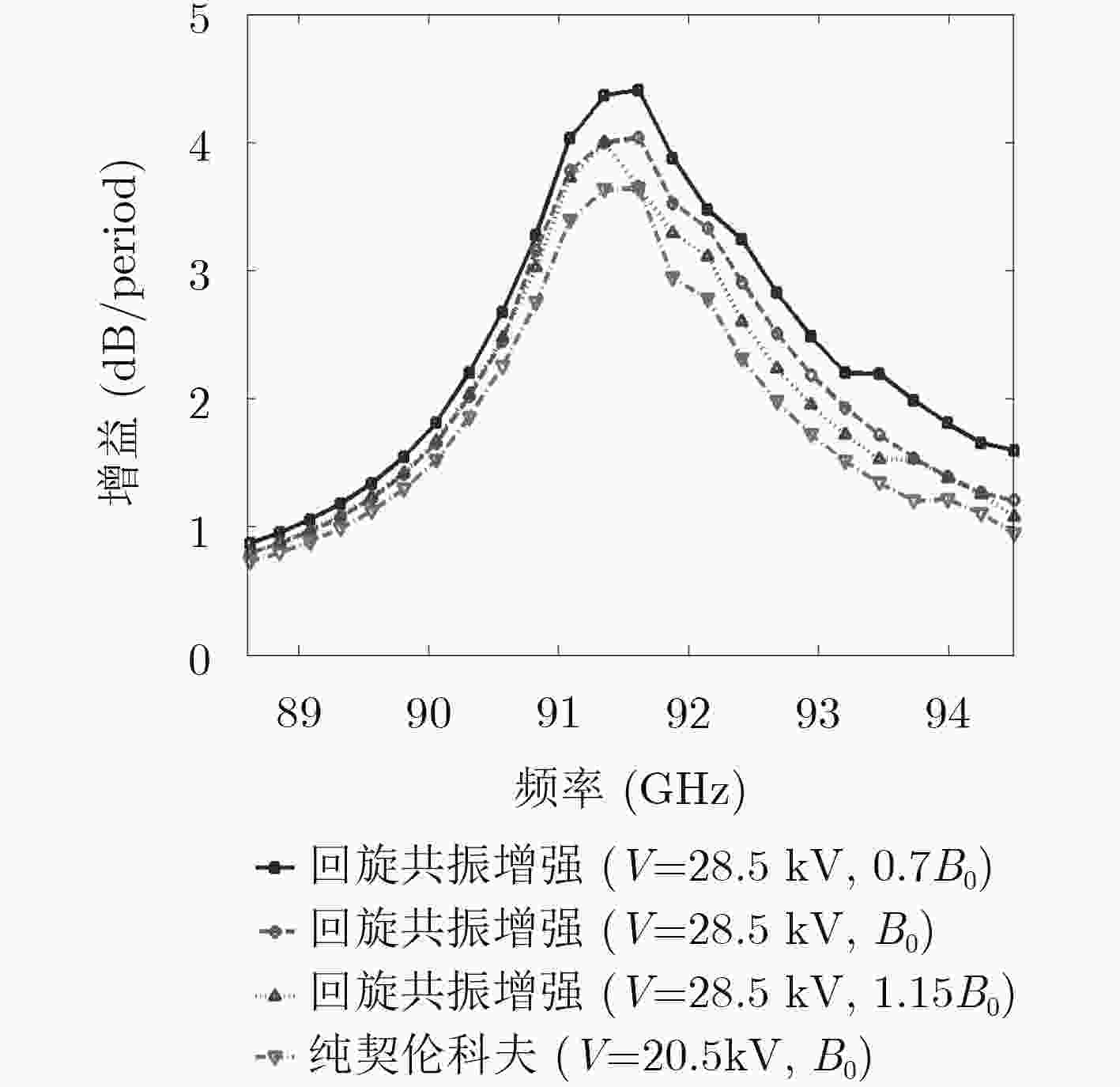



 下载:
下载:
