Blind Reconstruction of Convolutional Code Based on Partitioned Walsh-Hadamard Transform
-
摘要: 利用Walsh-Hadamard变换可实现2元域含错方程组的求解,该方法可用于卷积码的盲识别,但当方程组未知数较多时,其对计算机内存的要求使得该方法在实际中难以应用,为此该文提出一种基于分段Walsh-Hadamard变换的卷积码识别方法。该方法通过对方程组高维系数向量进行分段,使其转化为两个低维的系数向量,将Walsh-Hadamard变换求解高维方程组的问题分解为求解两个较低维数方程组的问题,同时证明了两个低维方程组解向量的组合就是高维方程组的解。算法有效减少了对计算机内存的需求,仿真结果验证了该算法的有效性,且算法具有良好的误码适应能力。
-
关键词:
- 卷积码 /
- 盲识别 /
- Walsh-Hadamard变换 /
- 含错方程 /
- 重构
Abstract: The Walsh-Hadamard transform can be used to solve binary domain error-containing equations, and the method can be used for blind identification of convolutional codes. However, when the number of system unknowns is large, the requirement of computer memory makes it difficult to apply this method to practice. Therefore, a convolutional code recognition method based on partitioned Walsh-Hadamard transform is proposed. By segmenting the high-dimensional coefficient vectors of the equations into two low-dimensional coefficient vectors, the problem of solving the high-dimensional equations by Walsh-Hadamard transformation is decomposed into the problem of solving the two low-dimensional equations, and it is proved that the combination of the solution vectors of the two low-dimensional equations is the solution of the high-dimensional equations. The algorithm reduces effectively the need for computer memory, and the simulation results verify the effectiveness of the proposed algorithm, and the algorithm has good error code adaptability. -
表 1 卷积码约束长度和输出路数估计算法
输入:接收到的码序列,分段长度l; 输出:卷积码输出路数n和约束长度K (1) 遍历卷积码输出路数$n'$,$2 \le n' \le 8$,令${K'} = 9$; (2) 将接收码序列排列成式(8)所示方程组,未知数个数为${n'}\!(\!{K'} \!\! +\! 1\!)$; (3)利用式(11)构造方程组系数对应的向量V,并按照l 将V进行矩
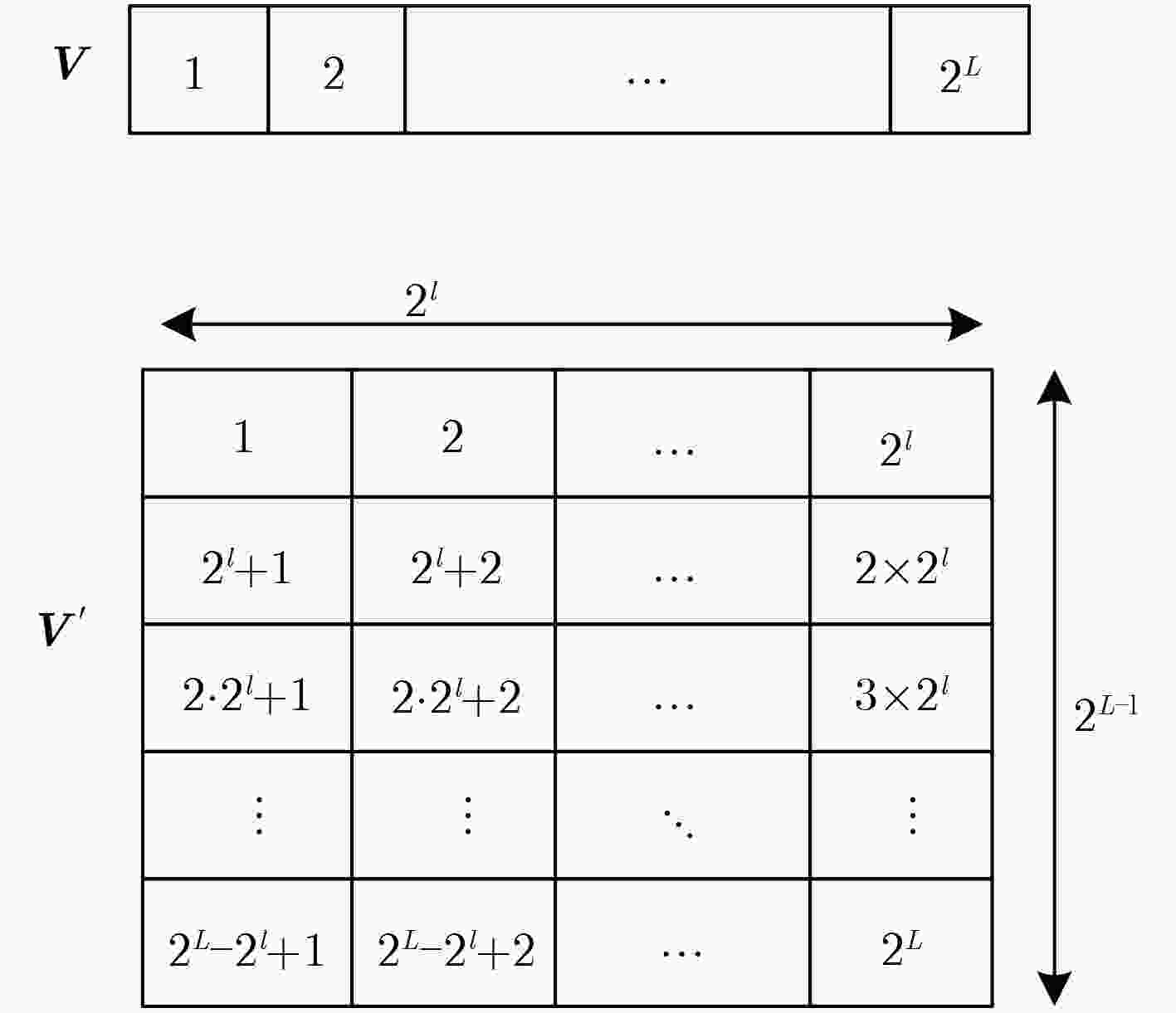
阵排列;(4) 令i从1到${2^{L - l}}$,其中$L = {n'}({K'} + 1)$,计算${\cal{H}}\left( {{{\text{V}}^l}} \right)$为
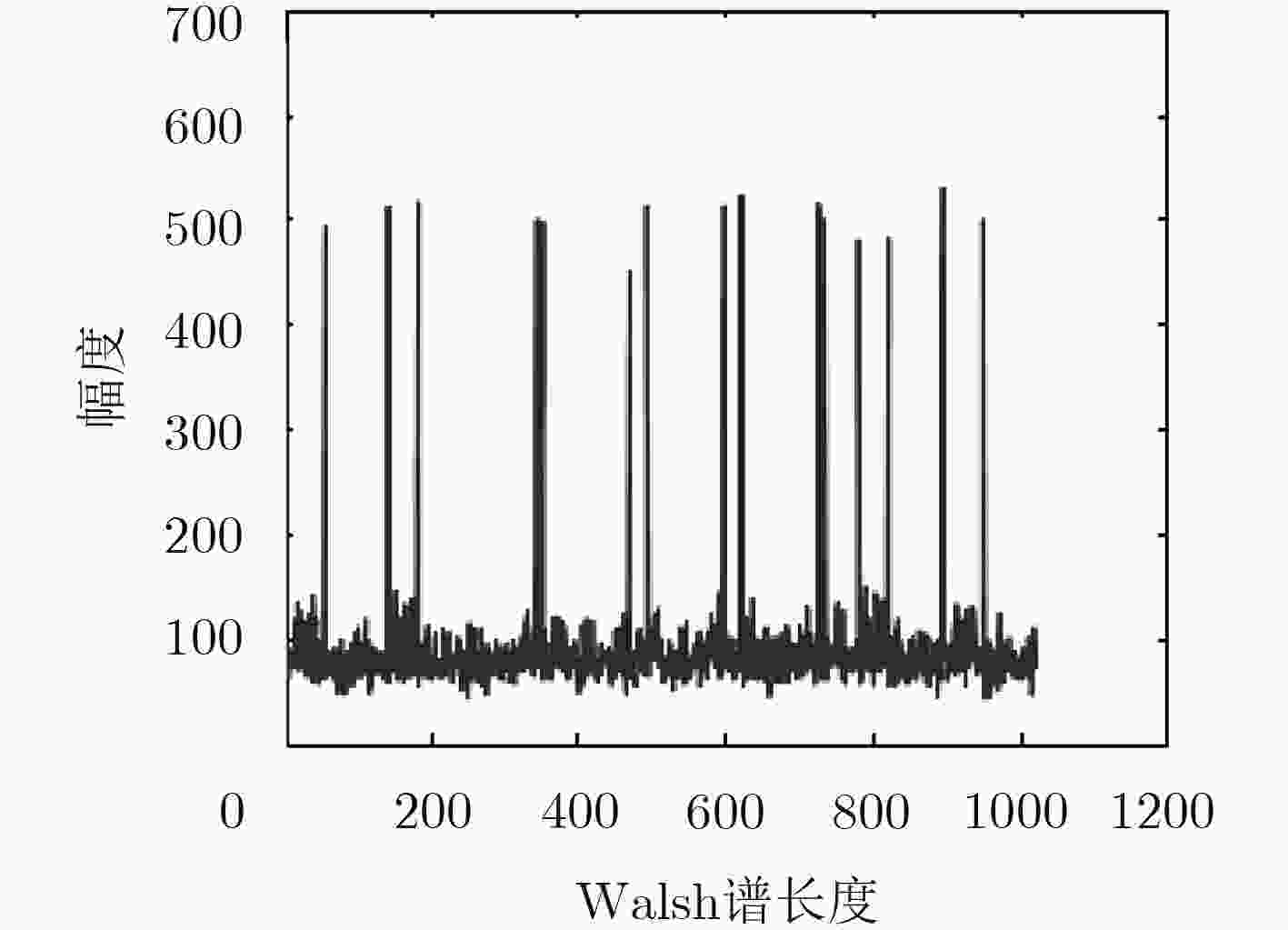
${\cal{H}}({{\text{V}}^l}) = \sum\limits_{i = 1}^{{2^{L - l}}} {{\rm{abs}} \left( {{\cal{H}}\left( {{{\text{V}}'}(i, :)} \right)} \right)} \qquad\qquad\qquad\qquad\qquad\quad\ (29)$(5) 如果${\cal{H}}\left( {{{\text{V}}^l}} \right)$中没有峰值,则返回(2),同时$n'$加1;如果${\cal{H}}\!\left(\! {{{\text{V}}^l}} \right)$ 存在m个峰值,表明此时$n = {n'}$,且$K = {K'} - {\log _2}(m + 1)$ (6) 输出K和n,或者序列中没有卷积码存在。 表 2 基于分段Walsh-hadamard变换的卷积码校验向量估计算法
输入:接收序列构成的方程组系数矩阵,其行向量维数为
$( K + 1)n$;分段的维数$l$;输出:方程组的L维解向量h。 (1) 根据式(11)计算方程组系数对应的向量V,并对V按长度${2^l}$进
行分段;(2) 令i从1~${2^{L - l}}$,其中$L = n(K \!+\! 1)$,计算每一行系数的Walsh
谱累积量${\cal{H}}\left( {{{\text{V}}^l}} \right)$为
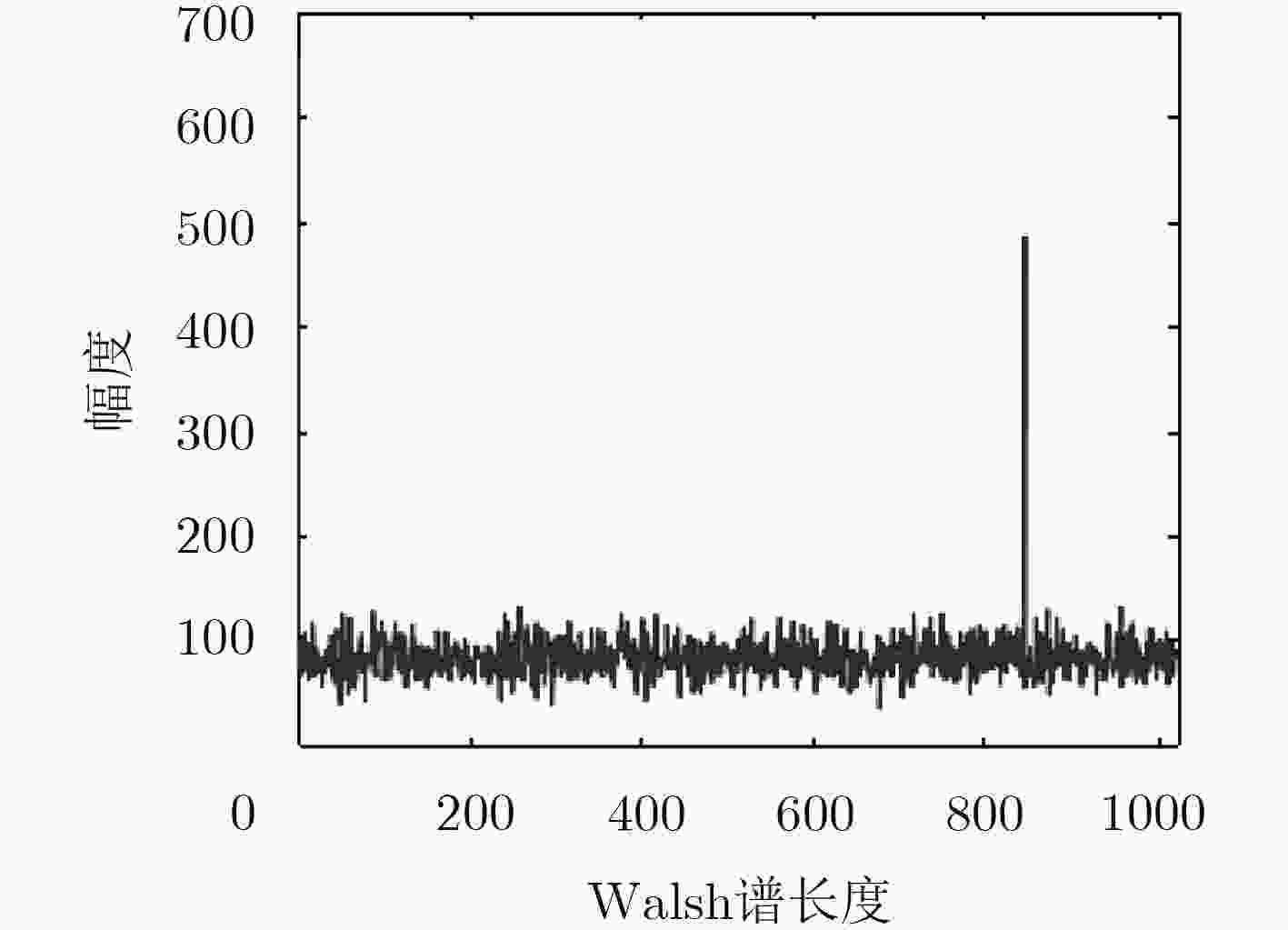
${\cal{H}}({{\text{V}}^l}) = \sum\limits_{i = 1}^{{2^{L - l}}} {{\rm{abs} }\left( {{\cal{H}}\left( {{{\text{V}}'}(i, :)} \right)} \right)} \qquad\qquad\qquad\qquad\qquad\quad\ (30)$(3) 在${\cal{H}}\left( {{{\text{V}}^l}} \right)$找出峰值位置,并将其转化为一个长度为l的二进
制向量${{\text{h}}_l}$;(4) 令j从1~${2^l}$,计算每一列系数的Walsh谱累积量为
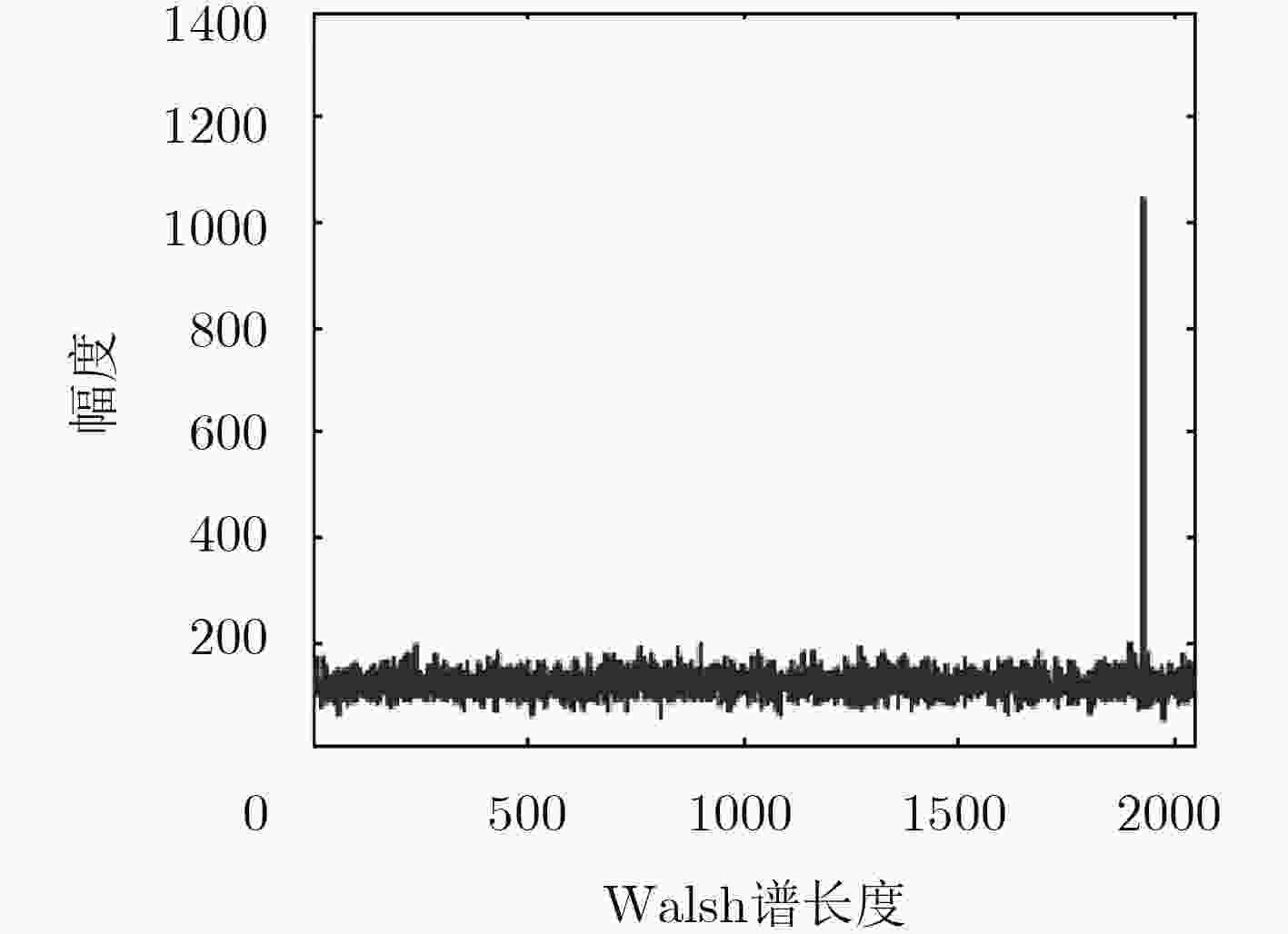
${\cal{H}}({{\text{V}}^{L - l}}) = \sum\limits_{j = 1}^{{2^l}} {{\rm{abs}} \left( {{\cal{H}}\left( {{{\text{V}}'}(:, j)} \right)} \right)} \qquad\qquad\qquad\qquad\qquad\ (31) $(5) 在${\cal{H}}({{\text{V}}^{L - l}})$找出峰值位置,并将其转化为一个长度为L-l的二
进制向量${{\text{h}}_{L - l}}$;(6) 令${\text{h}} = [{{\text{h}}_l} {{\text{h}}_{L - l}}]$,输出h。 -
任亚博. 误码条件下信道编码识别研究[D]. [博士论文], 清华大学, 2016.REN Yabo. Research on recognition algorithms of channel codes under error conditions[D]. [Ph.D. dissertation], Tsinghua University, 2016. 解辉, 黄知涛, 王丰华. 信道编码盲识别技术研究进展[J]. 电子学报, 2013, 41(6): 1166–1176. doi: 10.3969/j.issn.0372-2112.2013.06.019XIE Hui, HUANG Zhitao, and WANG Fenghua. Research progress of blind recognition of channel coding[J]. Acta Electronica Sinica, 2013, 41(6): 1166–1176. doi: 10.3969/j.issn.0372-2112.2013.06.019 解辉, 王丰华, 黄知涛, 等. 基于改进欧几里得算法的卷积码快速盲识别算法[J]. 国防科技大学学报, 2012, 34(6): 158–162. doi: 10.3969/j.issn.1001-2486.2012.06.028XIE Hui, WANG Fenghua, HUANG Zhitao, et al. A fast method for blind recognition of convolutional codes based on improved Euclidean algorithm[J]. Journal of National University of Defense Technology, 2012, 34(6): 158–162. doi: 10.3969/j.issn.1001-2486.2012.06.028 黄丽. 基于代数结构的交织器与卷积码的盲识别研究[D]. [博士论文], 中国科学技术大学, 2016.HUANG Li. Research on blind recognition of interleaver and convolutional encoders based on algebraic theory[D]. [Ph.D. dissertation], University of Science and Technology of China, 2016. 张立民, 刘杰, 钟兆根. (n, 1, m)递归系统卷积码的盲识别[J]. 电讯技术, 2014, 54(9): 1220–1225. doi: 10.3969/j.issn.1001-893x.2014.09.009ZHANG Limin, LIU Jie, and ZHONG Zhaogen. Blind recognition of (n, 1, m) recursive system convolutional code[J]. Telecommunication Engineering, 2014, 54(9): 1220–1225. doi: 10.3969/j.issn.1001-893x.2014.09.009 杨晓静, 刘建成, 张玉. 基于求解校验序列的(n, k, m)卷积码盲识别[J]. 宇航学报, 2013, 34(4): 568–573. doi: 10.3873/j.issn.1000-1328.2013.04.017YANG Xiaojing, LIU Jiancheng, and ZHANG Yu. Blind recognition of (n, k, m) convolutional codes based on solving check-sequence[J]. Journal of Astronautics, 2013, 34(4): 568–573. doi: 10.3873/j.issn.1000-1328.2013.04.017 韩树楠, 张旻, 李歆昊. 高容错(2, 1, m)卷积码快速盲识别方法[J]. 西安交通大学学报, 2017, 51(12): 28–34. doi: 10.7652/xjtuxb201712005HAN Shunan, ZHANG Min, and LI Xinhao. A fast method for blind identification of (2, 1, m) convolutional codes under high error bit ratios[J]. Journal of Xi’an Jiaotong University, 2017, 51(12): 28–34. doi: 10.7652/xjtuxb201712005 于沛东, 彭华, 巩克现, 等. 基于最小二乘代价函数的卷积码盲识别方法[J]. 电子学报, 2018, 46(7): 1545–1552. doi: 10.3969/j.issn.0372-2112.2018.07.002YU Peidong, PENG Hua, GONG Kexian, et al. Blind recognition of convolutional codes based on least-square cost-function[J]. Acta Electronica Sinica, 2018, 46(7): 1545–1552. doi: 10.3969/j.issn.0372-2112.2018.07.002 王伟年, 彭华, 冀磊. 倒谱与相位模糊条件下的卷积码高容错识别[J]. 信号处理, 2018, 34(4): 427–438. doi: 10.16798/j.issn.1003-0530.2018.04.006WANG Weinian, PENG Hua, and JI Lei. Robust recognition of convolutional codes with cepstrum and phase ambiguity[J]. Journal of Signal Processing, 2018, 34(4): 427–438. doi: 10.16798/j.issn.1003-0530.2018.04.006 张岱, 张玉, 杨晓静, 等. 基于遗传算法的(n, n-1, m)卷积码盲识别[J]. 火力与指挥控制, 2015, 40(9): 31–34. doi: 10.3969/j.issn.1002-0640.2015.09.007ZHANG Dai, ZHANG Yu, YANG Xiaojing, et al. Blind recognition of (n, n-1, m) convolutional code based on genetic algorithm[J]. Fire Control &Command Control, 2015, 40(9): 31–34. doi: 10.3969/j.issn.1002-0640.2015.09.007 陈泽亮, 巩克现, 彭华, 等. 基于软信息的分组交织和卷积码联合识别[J]. 电子学报, 2018, 46(6): 1454–1460. doi: 10.3969/j.issn.0372-2112.2018.06.026CHEN Zeliang, GONG Kexian, PENG Hua, et al. Joint blind recognition of packet interleaver and convolution code based on soft information[J]. Acta Electronica Sinica, 2018, 46(6): 1454–1460. doi: 10.3969/j.issn.0372-2112.2018.06.026 解辉, 王丰华, 黄知涛. 基于最大似然检测的(n, 1, m)卷积码盲识别方法[J]. 电子与信息学报, 2013, 35(7): 1671–1676. doi: 10.3724/sp.j.1146.2012.01578XIE Hui, WANG Fenghua, and HUANG Zhitao. Blind recognition of (n, 1, m) convolutional code based on maximum likelihood detection[J]. Journal of Electronics &Information Technology, 2013, 35(7): 1671–1676. doi: 10.3724/sp.j.1146.2012.01578 刘健, 王晓君, 周希元. 基于Walsh-Hadamard变换的卷积码盲识别[J]. 电子与信息学报, 2010, 32(4): 884–888. doi: 10.3724/SP.J.1146.2009.00359LIU Jian, WANG Xiaojun, and ZHOU Xiyuan. Blind recognition of convolutional coding based on Walsh-Hadamard transform[J]. Journal of Electronics &Information Technology, 2010, 32(4): 884–888. doi: 10.3724/SP.J.1146.2009.00359 张立民, 刘杰, 钟兆根. 基于改进Walsh-Hadamard变换的(n, 1, m)卷积码盲识别[J]. 电子与信息学报, 2018, 40(4): 839–845. doi: 10.11999/JEIT170605ZHANG Limin, LIU Jie, and ZHONG Zhaogen. Blind recognition of (n, 1, m) convolutional codes based on modified Walsh-Hadamard transform[J]. Journal of Electronics &Information Technology, 2018, 40(4): 839–845. doi: 10.11999/JEIT170605 张岱, 张玉, 杨晓静, 等. 基于分段抽取软判决加权Walsh Hadamard变换的卷积码识别算法[J]. 兵工学报, 2015, 36(12): 2298–2305. doi: 10.3969/j.issn.1000-1093.2015.12.012ZHANG Dai, ZHANG Yu, YANG Xiaojing, et al. An algorithm for convolutional codes recognition based on sectionally extracting soft-decision weighted Walsh Hadamard transform[J]. Acta Armamentarii, 2015, 36(12): 2298–2305. doi: 10.3969/j.issn.1000-1093.2015.12.012 WANG Fenghua, XIE Hui, and HUANG Zhitao. Blind reconstruction of convolutional code based on segmented Walsh-Hadamard transform[J]. Journal of Systems Engineering and Electronics, 2014, 25(5): 748–754. doi: 10.1109/JSEE.2014.00086 -





 下载:
下载:




 下载:
下载:
