A Distributed Node Localization Algorithm for Large Scale Sensor Networks
-
摘要: 针对大规模无线传感器网络(WSN)中节点难以定位的问题,该文提出一种基于改进牛顿法的分布式定位算法。该算法包括网络划分和分布式算法。首先,根据节点位置和节点之间直接相连的距离信息,将无线传感器网络划分为若干个重叠的子区域,并将子区域的定位问题归结为无约束优化问题,每个子区域可以独立计算;然后,使用分布式算法估计子区域中的节点位置并进行局部融合。实验结果表明,与已有算法相比,该算法具有良好的扩展性,在大规模网络中定位精度更高,能满足大规模无线传感器网络中节点定位需求。Abstract: A distributed algorithm based on modified Newton method is proposed to solve the nodes localization problem in large scale Wireless Sensor Network(WSN). The algorithm includes network partitioning and distributed algorithm. Firstly, the network is divided into several overlapping subregions according to the nodes positions and the distance information between the sensors. The localization problem of subregions is formulated into an unconstrained optimization problem and each subregion can be calculated independently. Then distributed algorithm is used to determine nodes positions in subregions and merge the subregions. Simulation results indicate that the proposed algorithm is superior to the existing algorithms in terms of accuracy in large scale network, which can meet the needs of nodes localization in large scale network.
-
表 1 子区域定位算法
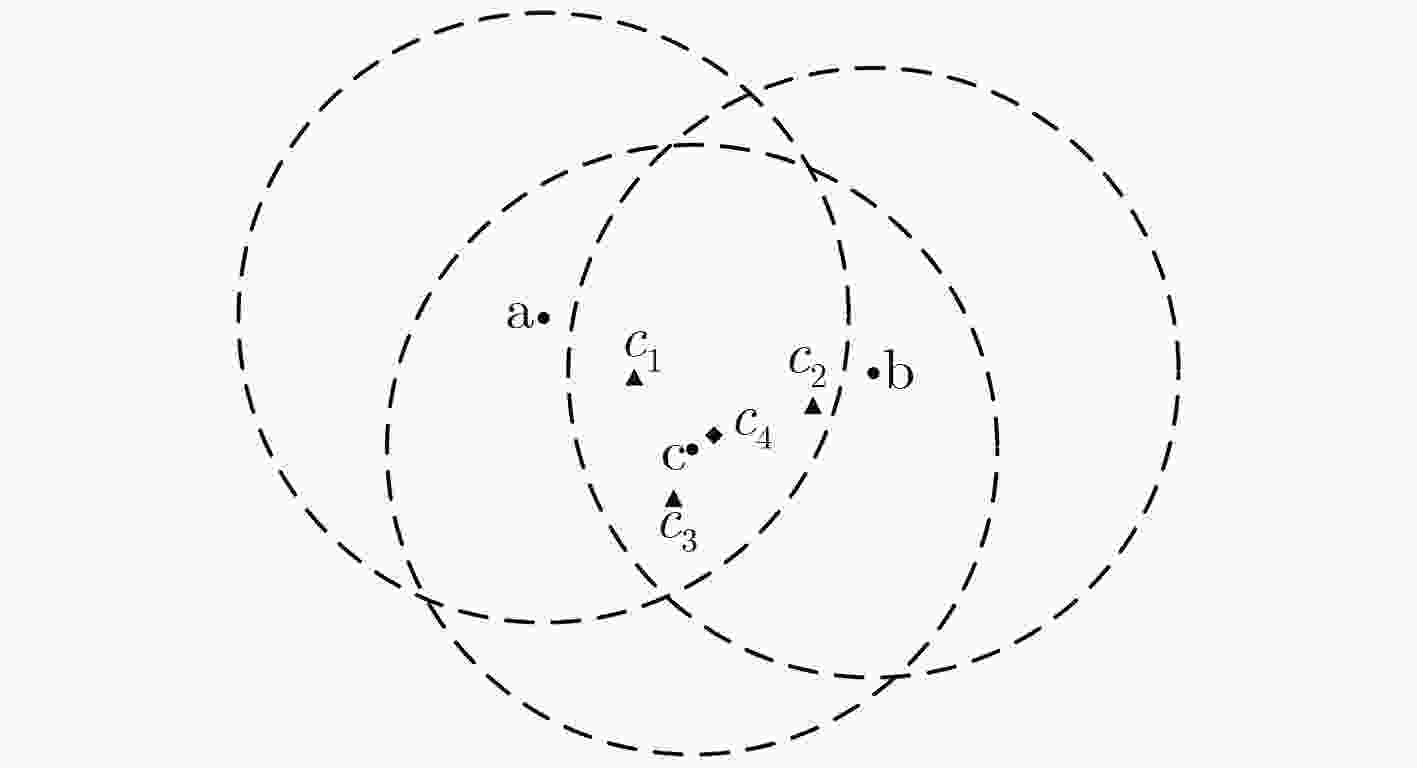
输入:使用三边定位方法,粗略获得LU节点的初始值,提取子区域$s$中LU节点的位置${{\text{p}}_k}$,作为初始值。设$k = 0$,表示第$k$次迭代; (1) 基于子区域目标函数$f({{\text{p}}_k})$,计算梯度向量$\nabla f({{\text{p}}_k})$和修正后的Hesse矩阵${\nabla ^2}f({{\text{p}}_k})$; (2) 计算搜索方向${{\text{q}}_k}$:${{\text{q}}_k} = - {\nabla ^2}f{({{\text{p}}_k})^{ - 1}}\nabla f({{\text{p}}_k})$; (3) 更新子区域$s$中LU节点位置,其中,步长设置为单位步长:${{\text{p}}_{k + 1}} = {{\text{p}}_k} + {{\text{q}}_k}$;
(4) 判断迭代终止条件。如果$\frac{{\left| {f({{\text{p}}_{k + 1}}) - f({{\text{p}}_k})} \right|}}{{1 + \left| {f({{\text{p}}_k})} \right|}} < \delta $($\delta $是一个很小的正数,本文设置为$\delta = 1e{\rm{ - }}9$)或迭代次数$k > 100$,则终止迭代,${{\text{p}}_{k + 1}}$即为
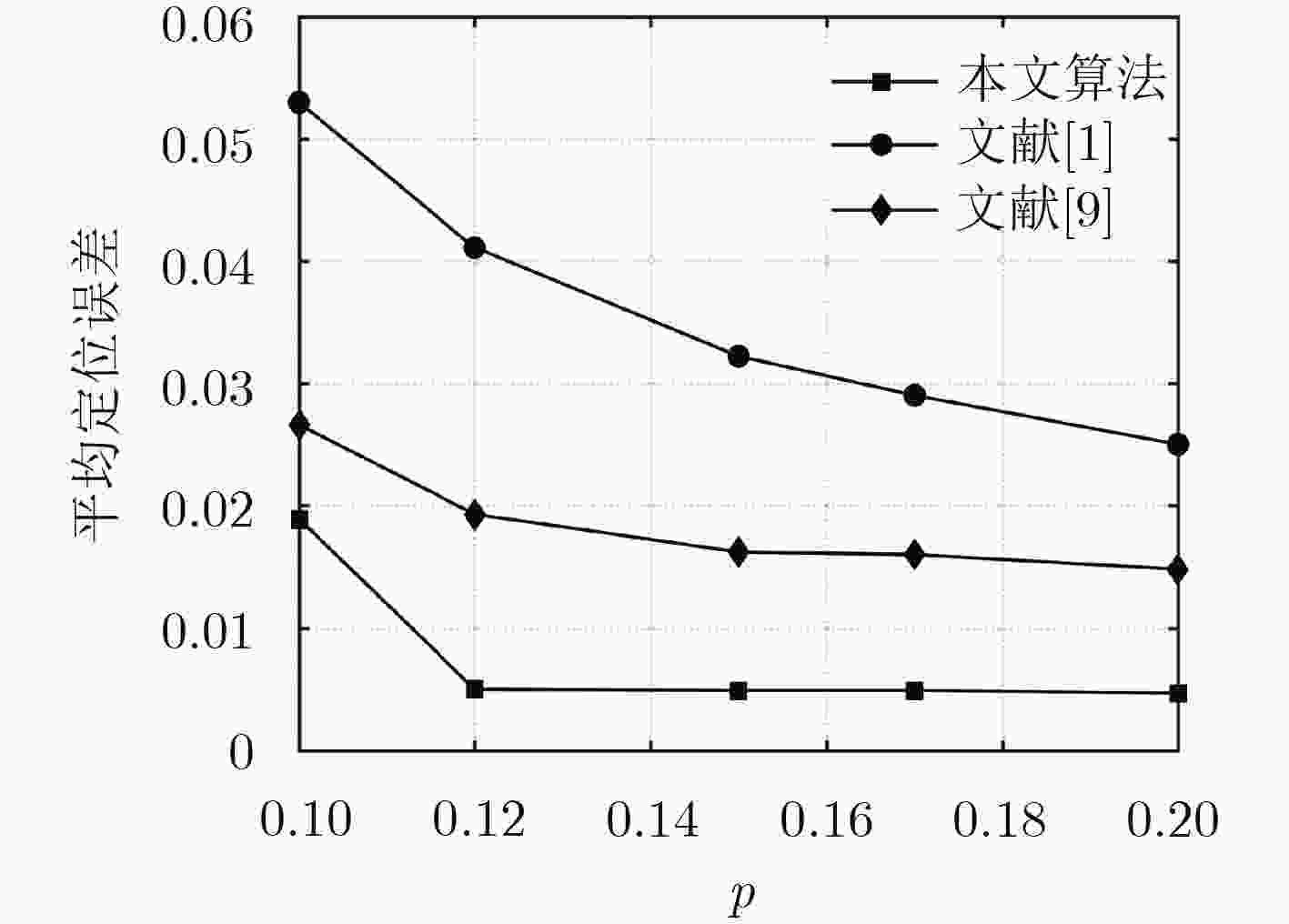
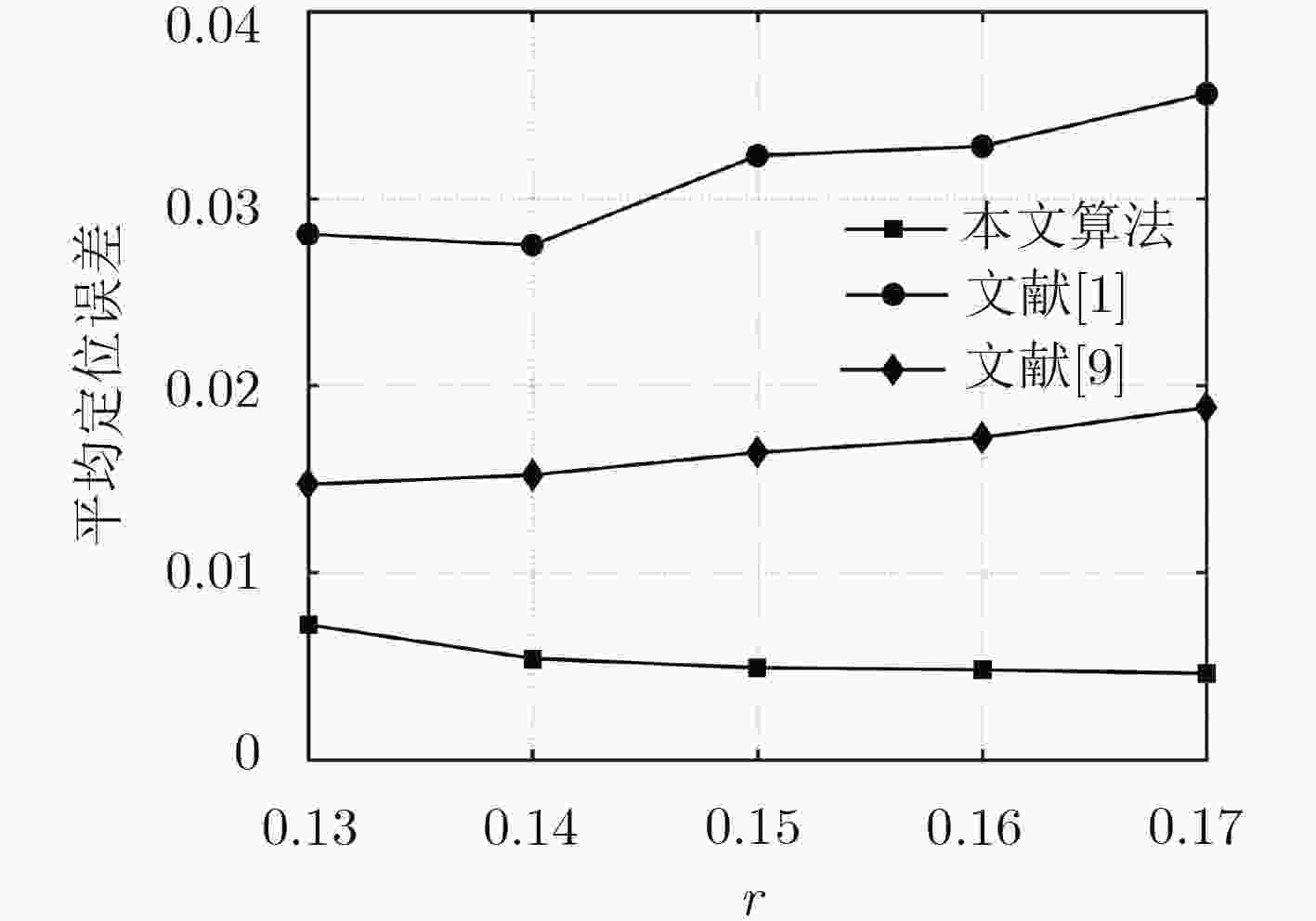
子区域优化最终结果;否则令$k = k + 1$,返回至第(1)步;输出:${{\text{p}}_{k + 1}}$。 参数设置 时间 ${\rm{\bar e\bar r\bar r}}$ $N$ $r$ ${\rm{nf}}$ 本文算法 文献[1] 文献[9] 文献[2] 本文算法 文献[1] 文献[9] 文献[2] 100 0.40 0 12.6 s 15.1 s 9.8 s 2.6 s 5.7e-4 0.0583 0.0489 6.5e-10 100 0.40 0.20 32.0 s 180.6 s 27.8 s 3.9 s 0.0114 0.0942 0.0746 0.0107 500 0.15 0 71.1 s 132.1 s 393.2 s 92.7 s 0.0011 0.0124 0.0025 4.0e-4 500 0.15 0.20 176.9 s 127.7 s 986.3 s 91.8 s 0.0048 0.0325 0.0164 0.0072 1000 0.11 0 309.2 s 348.7 s 51.0 min * 0.0015 0.0097 0.0026 * 1000 0.11 0.20 522.5 s 339.3 s 2.4 h * 0.0043 0.0249 0.0121 * 2000 0.07 0 369.1 s 760.5 s – * 0.0022 0.0209 – * 2000 0.07 0.20 576.2 s 649.5 s – * 0.0055 0.0241 – * 4000 0.05 0 555.9 s 23.1 min – * 0.0029 0.0266 – * 4000 0.05 0.20 840.3 s 27.5 min – * 0.0062 0.0238 – * 10000 0.03 0 23.3 min 1.1 h – * 0.0034 0.0172 – * 10000 0.03 0.20 31.6 min 1.2 h – * 0.0064 0.0147 – * 表 2 基于改进牛顿法的分布式定位算法
准备工作:将$N$个传感器随机部署在${[ - 0.5, 0.5]^2}$的单位正方形区域内,区域中有$m$个LU节点,$n$个LA节点,节点的通信半径均为$r$。根据 LU节点位置及与其直接相连的邻居节点,将WSN划分为$m$个重叠子区域,$m$个子区域可以进行分布式计算。设$t = 0$; 输入:利用三边定位方法获得WSN中LU节点的粗略估计值${\tilde{\text{v}}^{(t)}}$,作为基于单位步长改进牛顿法的初始值; (1) 利用表1中子区域定位算法,对$m$个子区域独立优化求解。得到每个子区域$s(s = 1, 2, \cdots , m)$中所有LU节点的估计位置${\text{p}}_s^{(t + 1)}$; (2) 收集$m$个子区域中LU节点估计位置${\text{p}}_s^{(t + 1)}(s = 1, 2, \cdots , m)$,对重叠子区域中的LU节点进行融合求平均,作为LU节点的估计位 置${\tilde{\text{v}}^{(t + 1)}}$;
(3) 判断迭代终止条件。如果${\rm{max}}{\left\| {\tilde {\text{v}}_i^{(t + 1)} - \tilde {\text{v}}_i^{(t)}} \right\|_2} \le \eta $($\eta $是一个小的正数,本文设置为$\eta = 1{\rm e}{\rm{ - } }2$), $i = 1, 2, ·\!·\!· , m$,则终止迭代,${\tilde{\text{v}}^{(t + 1)}}$ 即为最终估计出的LU节点位置;否则将${\tilde{\text{v}}^{(t + 1)}}$作为基于单位步长的改进牛顿法的初始值,设$t = t + 1$并返回至(1)继续迭代;输出:${\tilde {\text{v}}^{(t + 1)}}$。 -
SRIRANGARAJAN S, TEWFIK A H, and LUO Zhiquan. Distributed sensor network localization using SOCP relaxation[J]. IEEE Transactions on Wireless Communications, 2008, 7(12): 4886–4895. doi: 10.1109/T-WC.2008.070241 BISWAS P, LIANG T C, TOH K C, et al. Semidefinite programming approaches for sensor network localization with noisy distance measurements[J]. IEEE Transactions on Automation Science and Engineering, 2006, 3(4): 360–371. doi: 10.1109/TASE.2006.877401 PATWARI N, ASH J N, KYPEROUNTAS S, et al. Locating the nodes: cooperative localization in wireless sensor networks[J]. IEEE Signal Processing Magazine, 2005, 22(4): 54–69. doi: 10.1109/MSP.2005.1458287 VICENTE D, TOMIC S, BEKO M, et al. Performance analysis of a distributed algorithm for target localization in wireless sensor networks using hybrid measurements in a connection failure scenario[C]. 2017 International Young Engineers Forum, Almada, Portugal, 2017: 36–41. doi: 10.1109/YEF-ECE.2017.7935637. CHOWDHURY T J S, ELKIN C, DEVABHAKTUNI V, et al. Advances on localization techniques for wireless sensor networks: A survey[J]. Computer Networks, 2016, 110: 284–305. doi: 10.1016/j.comnet.2016.10.006 SANYAL R, JAISWAL M, and CHAUDHURY K N. On a registration-based approach to sensor network localization[J]. IEEE Transactions on Signal Processing, 2017, 65(20): 5357–5367. doi: 10.1109/TSP.2017.2726990 吕淑芳. 无线传感器网络节点定位研究综述[J]. 传感器与微系统, 2016, 35(5): 1–3. doi: 10.13873/J.1000-9787(2016)05-0001-03LÜ Shufang. Research review on wireless sensor networks node localization[J]. Transducer and Microsystem Technologies, 2016, 35(5): 1–3. doi: 10.13873/J.1000-9787(2016)05-0001-03 WANG Zizhuo, ZHENG Song, YE Yinyu, et al. Further relaxations of the semidefinite programming approach to sensor network localization[J]. SIAM Journal on Optimization, 2008, 19(2): 655–673. doi: 10.1137/060669395 SOARES C, XAVIER J, and GOMES J. Simple and fast convex relaxation method for cooperative localization in sensor networks using range measurements[J]. IEEE Transactions on Signal Processing, 2015, 63(17): 4532–4543. doi: 10.1109/TSP.2015.2454853 BISWAS P, LIAN T C, WANG T C, et al. Semidefinite programming based algorithms for sensor network localization[J]. ACM Transactions on Sensor Networks, 2006, 2(2): 188–220. doi: 10.1145/1149283.1149286 汪晗, 成昂轩, 王坤, 等. 无线传感器网络分布式迭代定位误差控制算法[J]. 电子与信息学报, 2018, 40(1): 72–78. doi: 10.11999/JEIT170344WANG Han, CHENG Angxuan, WANG Kun, et al. Error control algorithm of distributed localization in wireless sensor networks[J]. Journal of Electronics &Information Technology, 2018, 40(1): 72–78. doi: 10.11999/JEIT170344 TOMIC S, BEKO M, DINIS R, et al. Cooperative localization in wireless sensor networks using combined measurements[C]. The 23rd Telecommunications Forum Telfor, Belgrade, Serbia, 2015: 488–491. doi: 10.1109/TELFOR.2015.7377513. CHANG Shengming, LI Youming, WANG Hui, et al. RSS based cooperative localization in wireless sensor networks via second-order cone relaxation[J]. IEEE Access, 2018, 6: 54097–54105. doi: 10.1109/ACCESS.2018.2871600 王刚. 无线传感器网络中定位与跟踪算法的研究[D]. [博士论文], 西安电子科技大学, 2011.WANG Gang. Approaches to localization and tracking in wireless sensor networks[D]. [Ph.D. dissertation], Xidian University, 2011. 段琼, 戴璟, 乔慧. 一种改进的牛顿法及其在欧式距离选址模型中的应用[J]. 物流技术, 2017, 36(8): 79–82. doi: 10.3969/j.issn.1005-152X.2017.08.019DUAN Qiong, DAI Jing, and QIAO Hui. An improved newton method and its application in Euclidean distance based location model[J]. Logistics Technology, 2017, 36(8): 79–82. doi: 10.3969/j.issn.1005-152X.2017.08.019 蒋俊正. DFT调制滤波器组的设计算法研究[D]. [博士论文], 西安电子科技大学, 2011.JIANG Junzheng. Design algorithms of DFT modulated filter banks[D]. [Ph.D. dissertation], Xidian University, 2011. -





 下载:
下载:






 下载:
下载:
