|
CUI Guolong, YU Xianxiang, YANG Ya, et al. Cognitive phase-only sequence design with desired correlation and stopband properties[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2924–2935. doi: 10.1109/TAES.2017.2721238
|
|
DENG Hai. Effective CLEAN algorithms for performance-enhanced detection of binary coding radar signals[J]. IEEE Transactions on Signal Processing, 2004, 52(1): 72–78. doi: 10.1109/TSP.2003.820075
|
|
BLUNT S D and GERLACH K. Adaptive pulse compression via MMSE estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 572–584. doi: 10.1109/TAES.2006.1642573
|
|
李秀友, 董云龙, 黄勇, 等. 基于迭代线性约束最小方差的稳健自适应脉冲压缩方法[J]. 电子与信息学报, 2015, 37(10): 2300–2306. doi: 10.11999/JEIT141631LI Xiuyou, DONG Yunlong, HUANG Yong, et al. Robust adaptive pulse compression algorithm based on reiterative linearly constrained minimum variance[J]. Journal of Electronics &Information Technology, 2015, 37(10): 2300–2306. doi: 10.11999/JEIT141631
|
|
XU Xiaojian and NARAYANAN R M. Range sidelobe suppression technique for coherent ultra wide-band random noise radar imaging[J]. IEEE Transactions on Antennas and Propagation, 2001, 49(12): 1836–1842. doi: 10.1109/8.982467
|
|
HE Hao, LI Jian, and STOICA P. Waveform Design for Active Sensing Systems: A Computational Approach[M]. Cambridge, New York, USA: Cambridge University Press, 2012: 29–65.
|
|
李风从, 赵宜楠, 乔晓林. 抑制特定区间距离旁瓣的恒模波形设计方法[J]. 电子与信息学报, 2013, 35(3): 532–536. doi: 10.3724/SP.J.1146.2012.00857LI Fengcong, ZHAO Yinan, and QIAO Xiaolin. Constant modular waveform design method for suppressing range sidelobes in specified intervals[J]. Journal of Electronics &Information Technology, 2013, 35(3): 532–536. doi: 10.3724/SP.J.1146.2012.00857
|
|
HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30–40. doi: 10.1109/MSP.2006.1593335
|
|
GUI Ronghua, WANG Wenqin, PAN Ye, et al. Cognitive target tracking via angle-range-Doppler estimation with transmit subaperturing FDA radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 76–89. doi: 10.1109/JSTSP.2018.2793761
|
|
邹鲲, 骆艳卜, 李伟, 等. 频谱拥挤环境中峰均功率比约束的认知雷达发射波形设计[J]. 电子与信息学报, 2018, 40(7): 1774–1778. doi: 10.11999/JEIT170834ZOU Kun, LUO Yanbo, LI Wei, et al. Cognitive radar waveform design with a peak to average power ration constraint for spectrally dense environments[J]. Journal of Electronics &Information Technology, 2018, 40(7): 1774–1778. doi: 10.11999/JEIT170834
|
|
CHEN Peng and WU Lenan. Waveform design for multiple extended targets in temporally correlated cognitive radar system[J]. IET Radar, Sonar & Navigation, 2016, 10(2): 398–410. doi: 10.1049/iet-rsn.2015.0295
|
|
GUIMARÃES D A and LIM C H. Sliding-window-based detection for spectrum sensing in radar bands[J]. IEEE Communications Letters, 2018, 22(7): 1418–1421. doi: 10.1109/LCOMM.2018.2834932
|
|
SHARAGA N, TABRIKIAN J, and MESSER H. Optimal cognitive beamforming for target tracking in MIMO radar/sonar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1440–1450. doi: 10.1109/JSTSP.2015.2467354
|
|
郝天铎, 周青松, 孙从易, 等. 非准确先验知识下认知雷达低峰均比稳健波形设计[J]. 电子与信息学报, 2018, 40(3): 532–540. doi: 10.11999/JEIT170560HAO Tianduo, ZHOU Qingsong, SUN Congyi, et al. Low-PAR robust waveform design for cognitive radar with imprecise prior knowledge[J]. Journal of Electronics &Information Technology, 2018, 40(3): 532–540. doi: 10.11999/JEIT170560
|
|
XIONG Jie, WANG Wenqin, CUI Can, et al. Cognitive FDA-MIMO radar for LPI transmit beamforming[J]. IET Radar, Sonar & Navigation, 2017, 11(10): 1574–1580. doi: 10.1049/iet-rsn.2016.0551
|
|
GARREN D A, OSBORN M K, ODOM A C, et al. Enhanced target detection and identification via optimised radar transmission pulse shape[J]. IEE Proceedings - Radar, Sonar and Navigation, 2001, 148(3): 130–138. doi: 10.1049/ip-rsn:20010324
|
|
ZHANG X and CUI Can. Signal detection for cognitive radar[J]. Electronics Letters, 2013, 49(8): 559–560. doi: 10.1049/el.2012.3345
|
|
冯翔, 陈志坤, 赵宜楠, 等. 基于联合优化松弛交替投影的组网雷达恒模波形设计[J]. 电子与信息学报, 2016, 38(7): 1745–1751. doi: 10.11999/JEIT151152FENG Xiang, CHEN Zhikun, ZHAO Yinan, et al. Unimodular waveforms design for netted radar system via joint optimization relaxed alternating projection[J]. Journal of Electronics &Information Technology, 2016, 38(7): 1745–1751. doi: 10.11999/JEIT151152
|
|
ZHUANG Shanna, WANG Zhengyou, and WANG Hui. Waveform optimization to improve MIMO radar range-angle imaging performance[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 56–61. doi: 10.1109/RADAR.2015.7130970.
|





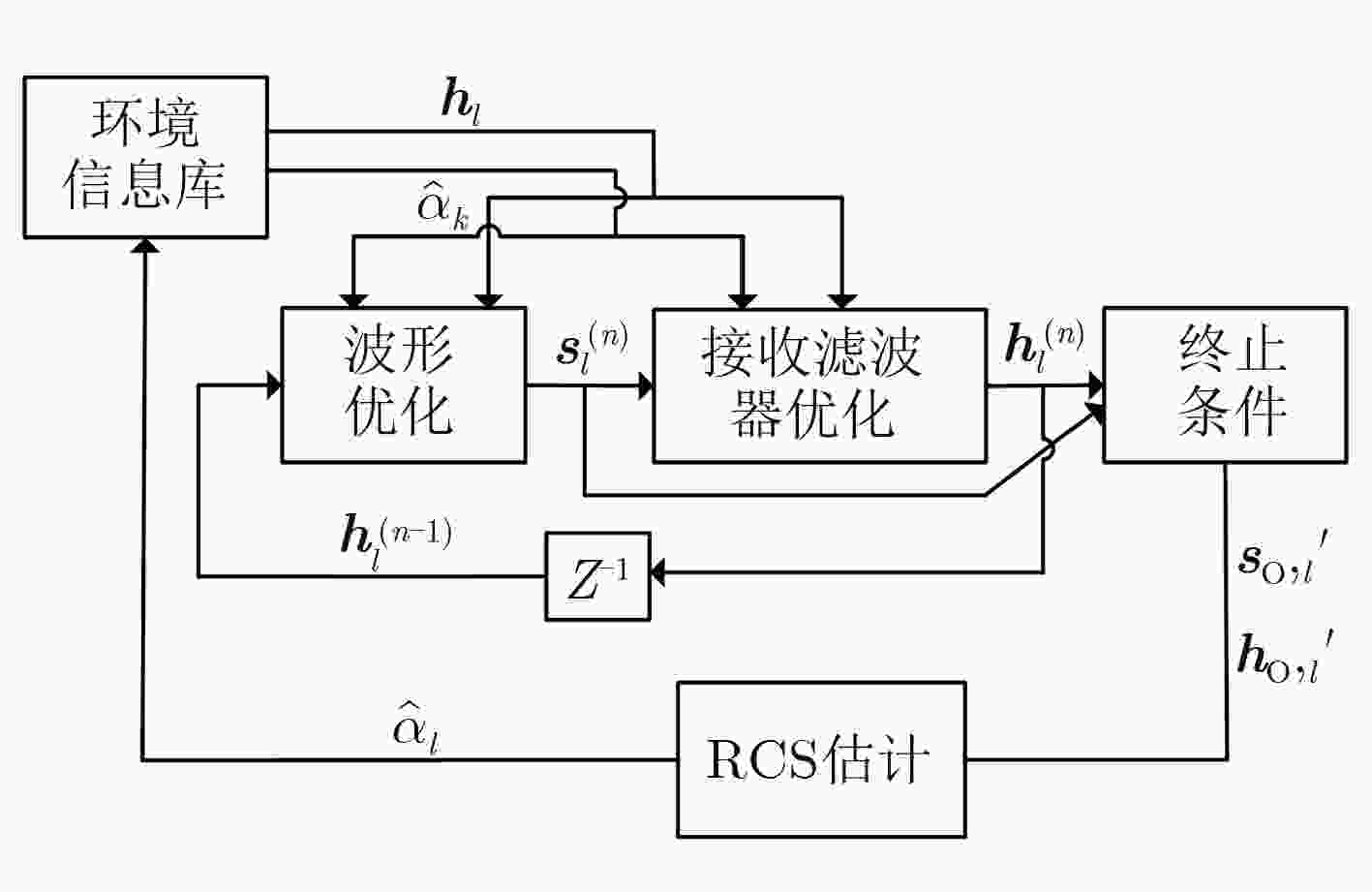
 下载:
下载:
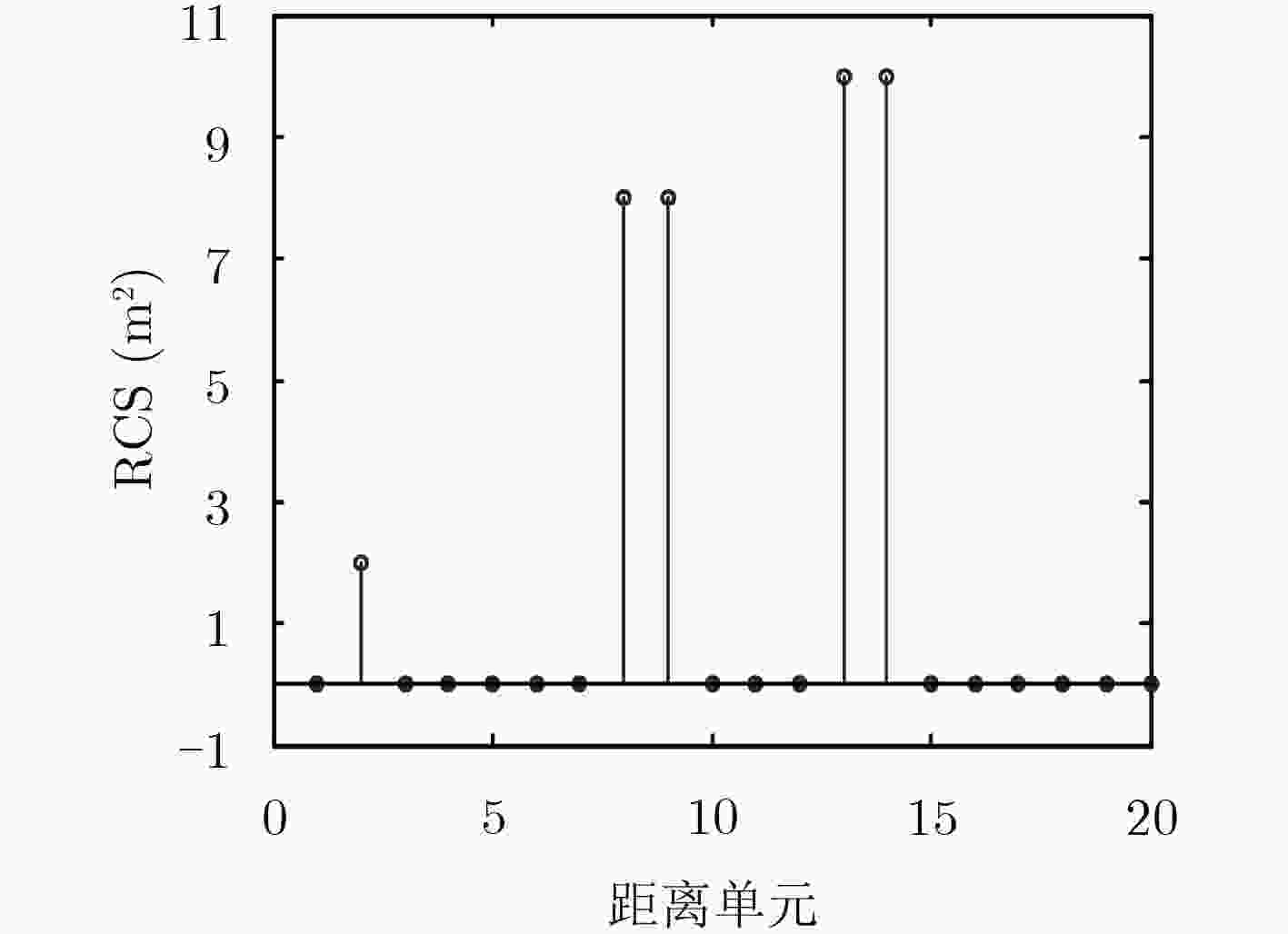
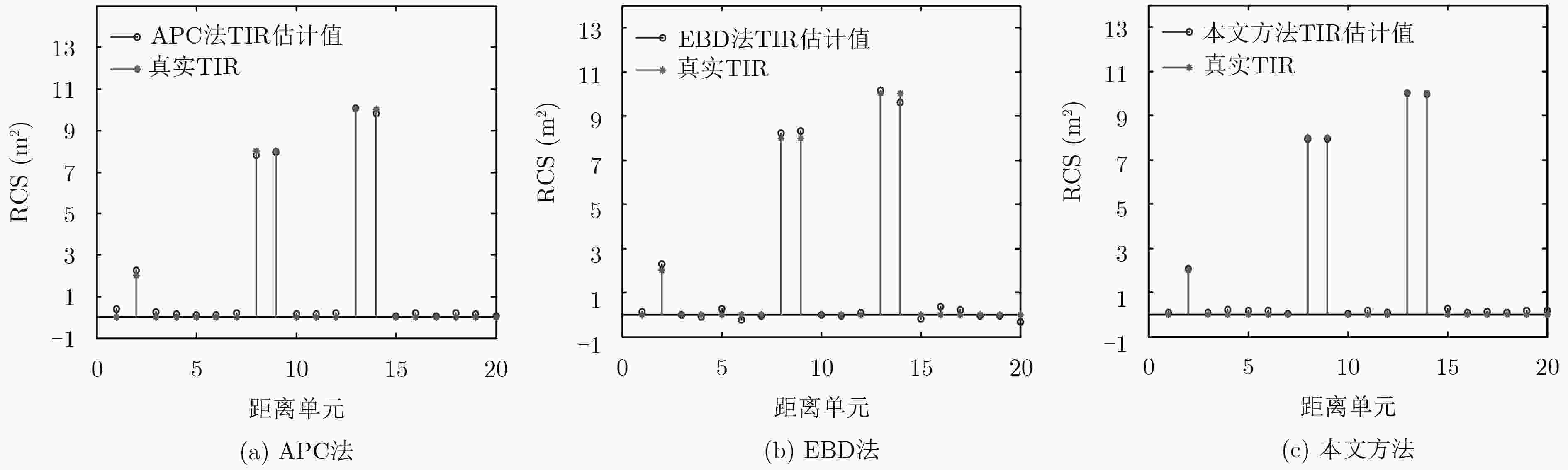

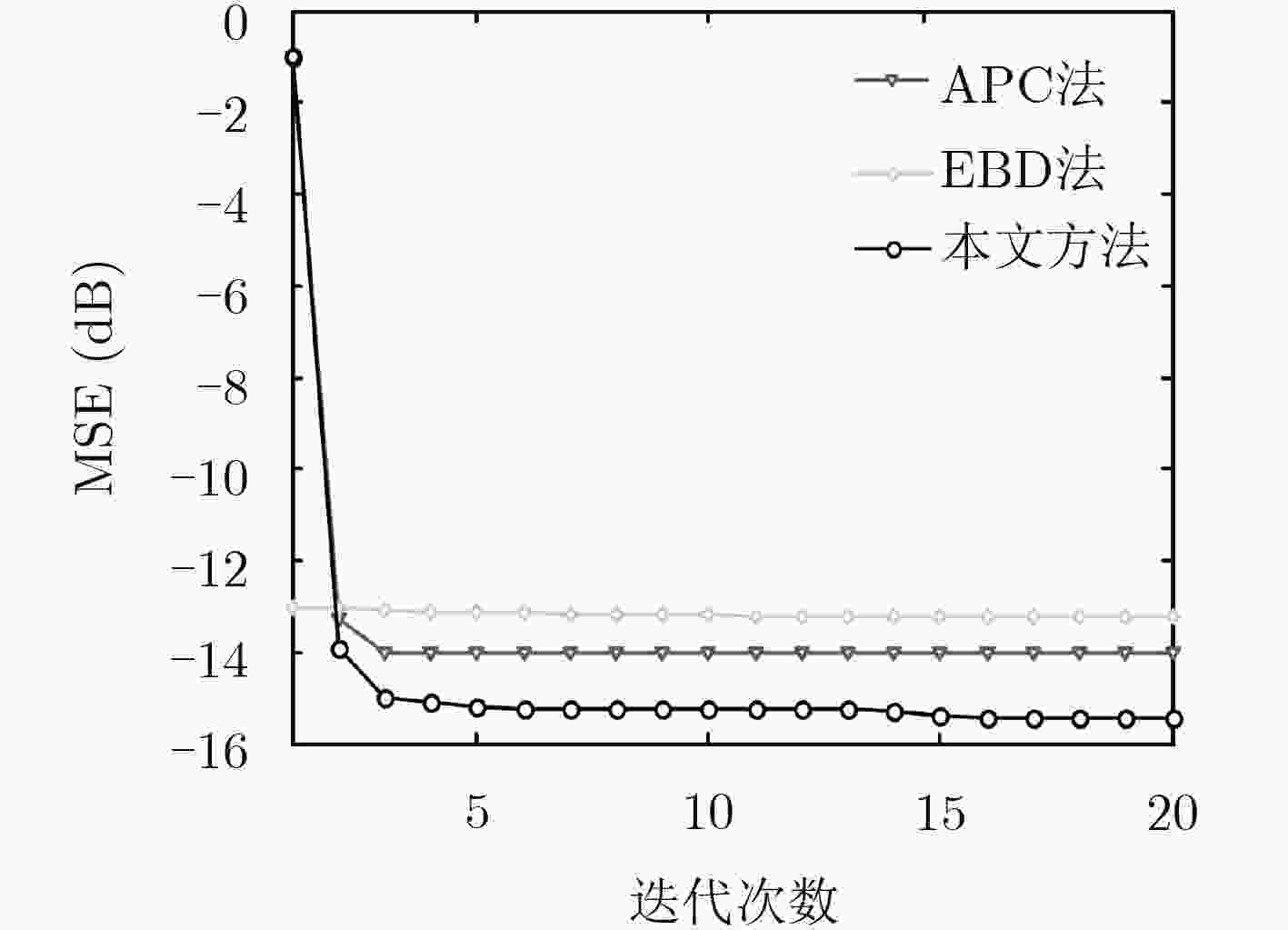



 下载:
下载:
