High Frequency Surface Wave Radar Detector Based on Log-determinant Divergence and Symmetrized Log-determinant Divergence
-
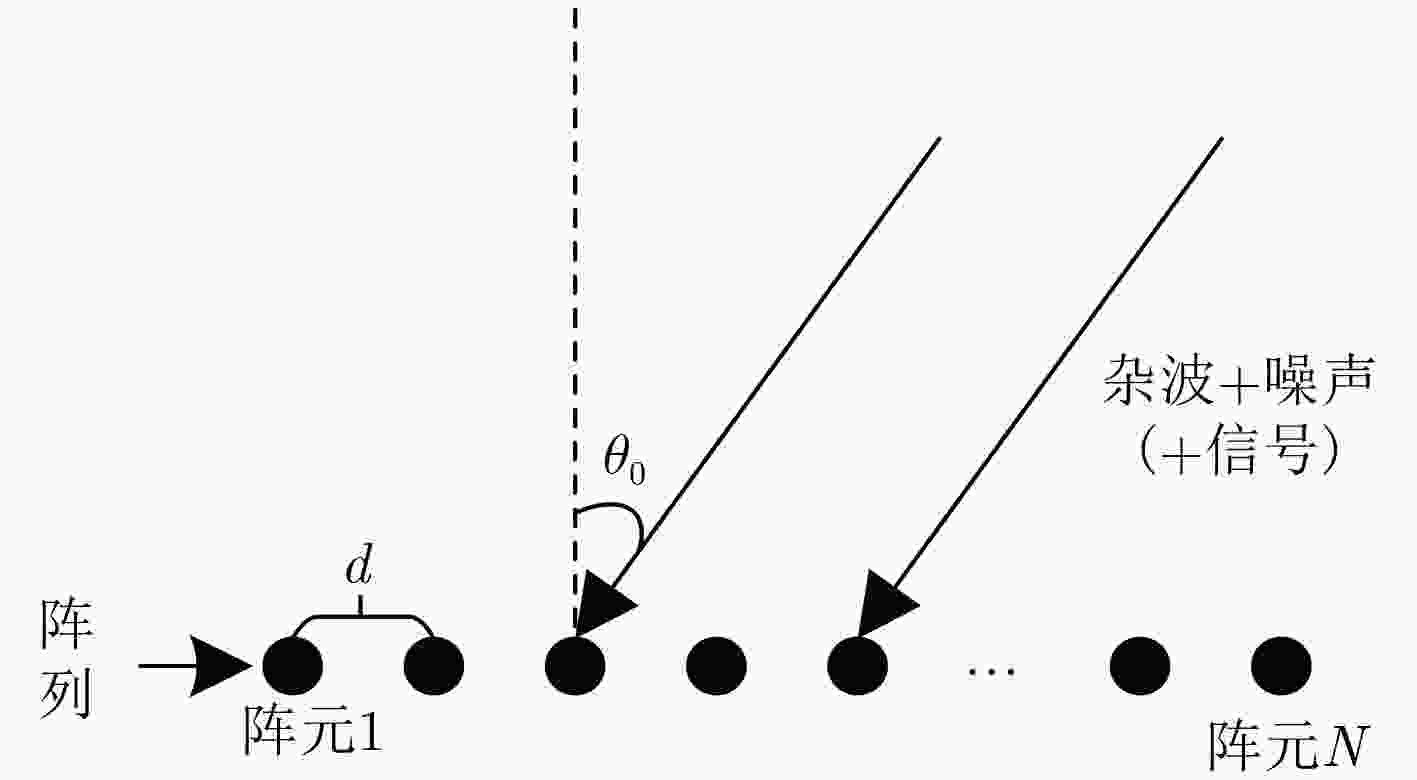
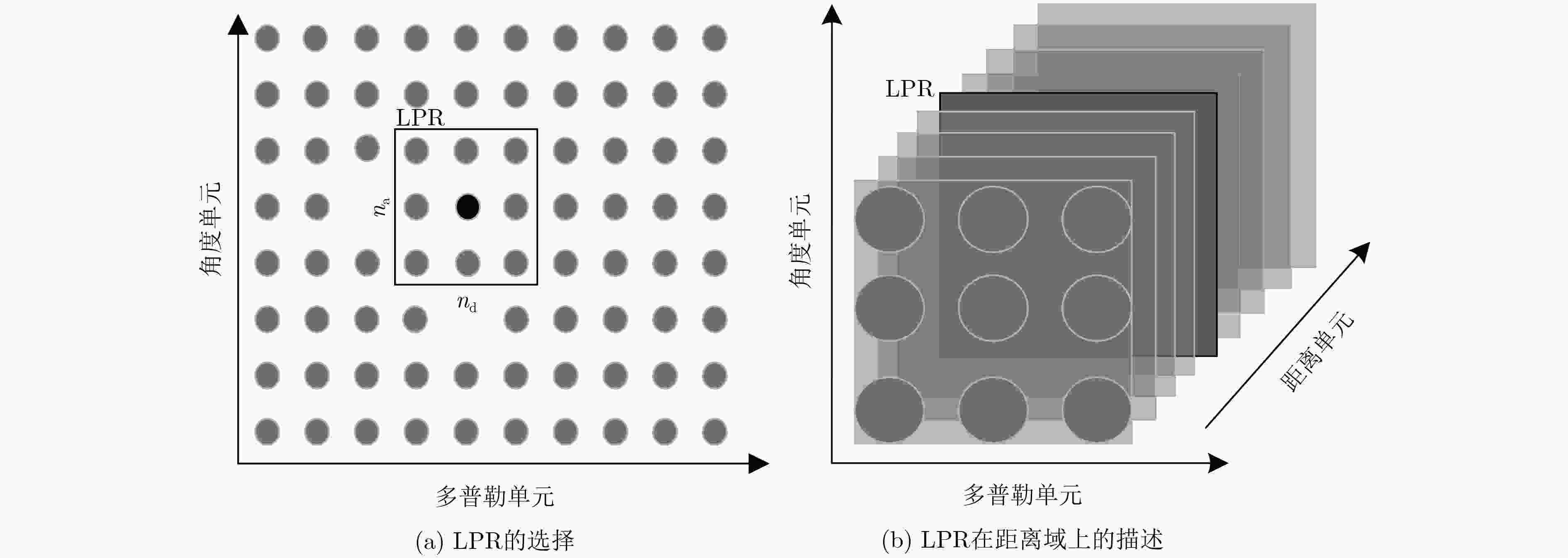
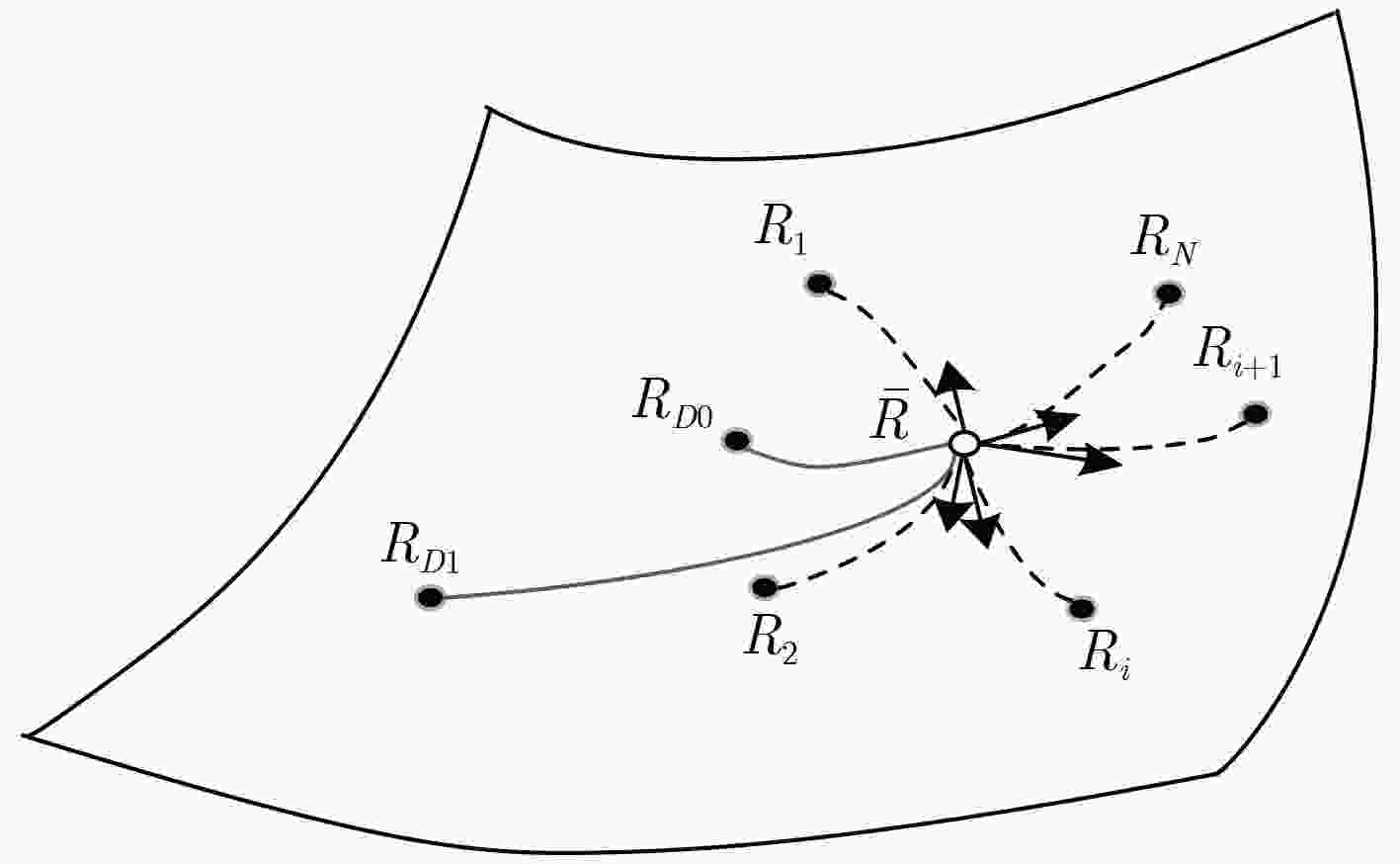
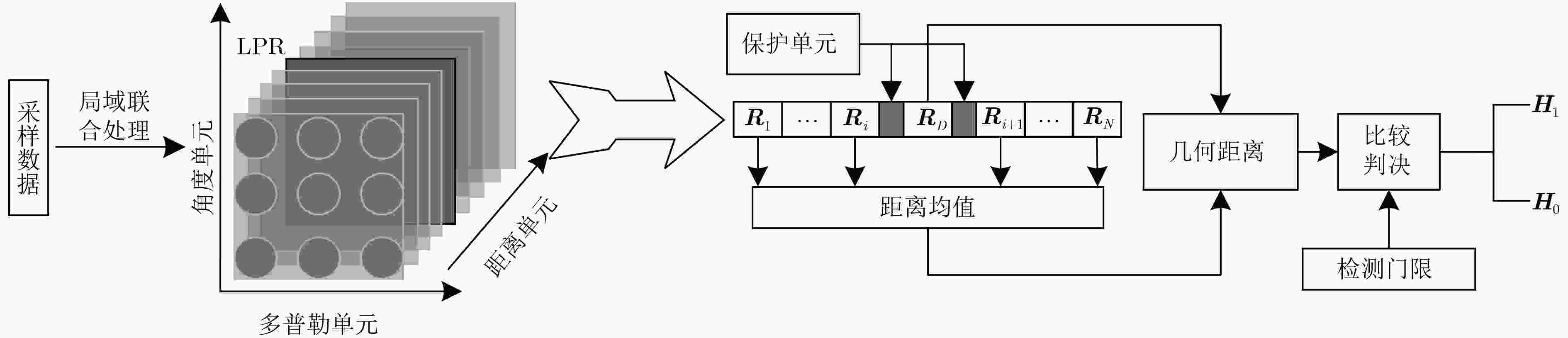
摘要: 高频地波雷达(HFSWR)利用电磁波绕射原理进行目标探测,具有超视距的特性。然而,探测距离的增加会使得雷达目标回波能量减弱,进而使得雷达探测能力下降。为了改善高频地波雷达的探测性能,该文提出了一种基于信息几何理论的局域联合矩阵恒虚警率(CFAR)检测器,利用信号在角度、多普勒速度和距离的多维信息进行检测;并使用对数行列式散度(LDD)和对称对数行列式散度(SLDD)代替黎曼距离(RD)作为距离度量。最后,实验结果验证了该文提出的检测器能够有效地改善雷达对目标的检测性能。Abstract: High Frequency Surface Wave Radar (HFSWR) utilizes electromagnetic wave diffracting along the earth to detect targets over the horizon. However, the increase of target distance decreases the received echo energy, and this degrades the detection capability. A joint domain matrix Constant False Alarm Rate (CFAR) detector is proposed to improve the detection performance. It employs the multi-dimensional information of signal in azimuth, Doppler velocity and range domain to detect target, and Log-Determinant Divergence (LDD) and Symmetrized Log-Determinant Divergence (SLDD) are used to replace the Riemannian Distance (RD) as the measure of distance. Finally, the experiment results show that the detector presented by the paper can improve the detection performance effectively.
-
表 1 不同距离度量方法及其几何均值
度量方法 距离计算 几何均值 RD ${{{D}}_R}^2({{{R}}_1},{{{R}}_2}) = {\rm{tr}}[{\lg ^2}({{{R}}_1}^{ - 1/2}{{{R}}_2}{{{R}}_1}^{ - 1/2})] $ ${\bar {{R}}_{t + 1}} = \bar {{R}}_t^{1/2}\exp \left[{\rm{ds}} \cdot \frac{1}{N}\mathop \displaystyle\sum \limits_{i = 1}^N \lg (\bar {{R}}_t^{ - 1/2}{{{R}}_i}\bar {{R}}_t^{ - 1/2})\right]\bar {{R}}_t^{1/2}$ LDD ${{{D}}_{\rm{LD}}}({{{R}}_1},{{{R}}_2}) = {\rm{tr}}({{R}}_2^{ - 1}({{{R}}_1} - {{{R}}_2})) - \ln \det({{R}}_2^{ - 1}{{{R}}_1})$ $\bar {{R}} = {\left( {\frac{1}{N}\mathop \sum \limits_{k = 1}^N {{R}}_k^{ - 1}} \right)^{ - 1}}$ SLDD $\begin{aligned} {{{D}}_{{\rm{SLD}}}}({{{R}}_1},{{{R}}_2}) =& \frac{1}{2}({\rm{tr}}({{R}}_2^{ - 1}({{{R}}_1} - {{{R}}_2})) - \ln \det({{R}}_2^{ - 1}{{{R}}_1}) \\ & + {\rm{tr}}({{R}}_1^{ - 1}({{{R}}_2} - {{{R}}_1})) - \ln \det({{R}}_1^{ - 1}{{{R}}_2})) \\ \end{aligned} $ $\bar {{R}} = {\left( {\frac{1}{N}\mathop \sum \limits_{k = 1}^N {{R}}_k^{ - 1}} \right)^{ - 1}}$ 表 2 基本矩阵运算的复杂度
矩阵运算 表达式 浮点数计算次数 矩阵运算 表达式 浮点数计算次数 矩阵乘法 ${{{R}}_1}{{{R}}_2}$ $8{n^3} - 2{n^2}$ 矩阵求逆 ${{R}}_1^{ - 1}$ $8{n^3} - 2{n^2}$ 矩阵加法 ${{{R}}_1}{{ + }}{{{R}}_2}$ $2{n^2}$ 矩阵开方 ${{R}}_1^{1/2}$ $24{n^3} + 2{n^2} - 8n$ 矩阵的迹 ${\rm{tr}}({{{R}}_1})$ $8{n^2} - 6n - 2$ 矩阵指数 $\exp ({{{R}}_1})$ ${n^4}/2 + 24{n^3} + 1.5{n^2} - n$ 矩阵行列式 $\det ({{{R}}_1})$ $8{n^2} - 2n - 6$ 矩阵对数 $\lg ({{{R}}_1})$ ${n^4}/2 + 25{n^3} + {n^2} - 1.5n$ 表 3 不同距离度量方法的复杂度
度量方法 距离计算复杂度 几何均值计算复杂度 RD ${n^4}/2 + 73{n^3} + 5{n^2} - 15.5n - 1$ $(N + 1){n^4}/2 + (41N + 88){n^3} - (N + 6.5){n^2} - (1.5N + 9)n$ LDD $16{n^3} + 14{n^2} - 8n - 6$ $8(N + 1){n^3} - 2{n^2}$ SLDD $32{n^3} + 28{n^2} - 15n - 11$ $8(N + 1){n^3} - 2{n^2}$ -
姚迪, 张鑫, 杨强, 等. 基于空间多波束的高频地波雷达电离层杂波抑制算法[J]. 电子与信息学报, 2017, 39(12): 2827–2833. doi: 10.11999/JEIT170477YAO Di, ZHANG Xin, YANG Qiang, et al. Ionospheric clutter suppression algorithm based on space multibeam for high frequency surface wave radar[J]. Journal of Electronics &Information Technology, 2017, 39(12): 2827–2833. doi: 10.11999/JEIT170477 WANG Yiming, MAO Xingpeng, ZHANG Jie, et al. Detection of vessel targets in sea clutter using in situ sea state measurements with HFSWR[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 302–306. doi: 10.1109/LGRS.2017.2786725 杨强, 刘永坦. 复杂背景下的二维检测研究[J]. 系统工程与电子技术, 2002, 24(1): 34–37. doi: 10.3321/j.issn:1001-506X.2002.01.010YANG Qiang and LIU Yongtan. 2-D detection in complex background[J]. Systems Engineering and Electronics, 2002, 24(1): 34–37. doi: 10.3321/j.issn:1001-506X.2002.01.010 TURLEY M D E. Hybrid CFAR techniques for HF radar[C]. Radar 97, Edinburgh, UK, 1997: 36–40. LI Yang, ZHANG Ning, and YANG Qiang. Characteristic-knowledge-aided spectral detection of high frequency first-order sea echo[J]. Journal of Systems Engineering and Electronics, 2009, 20(4): 718–725. WANG Hong and CAI Lujing. On adaptive spatial-temporal processing for airborne surveillance radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 660–670. doi: 10.1109/7.303737 ZHANG Xin, SU Yanhua, YANG Qiang, et al. Space-time adaptive processing-based algorithm for meteor trail suppression in high-frequency surface wave radar[J]. IET Radar, Sonar & Navigation, 2015, 9(4): 429–436. doi: 10.1049/iet-rsn.2014.0300 衣春雷. 船载高频地波雷达海杂波抑制方法研究[D].[博士论文], 哈尔滨工业大学, 2017.YI Chunlei. Study on sea clutter suppression for shipborne high frequency surface wave radar[D]. [Ph.D. dissertation], Harbin Institute of Technology, 2017. RADHAKRISHNA RAO C. Information and the accuracy attainable in the estimation of statistical parameters[J]. Bulletin of the Calcutta Mathematical Society, 1945, 37(3): 81–91. WANG Meng, NING Zhenhu, XIAO Chuangbai, et al. Sentiment classification based on information geometry and deep belief networks[J]. IEEE Access, 2018, 6: 35206–35213. doi: 10.1109/ACCESS.2018.2848298 黎湘, 程永强, 王宏强, 等. 雷达信号处理的信息几何方法[M]. 北京: 科学出版社, 2014: 13: 18. ZHANG Fode, NG H K T, and SHI Yimin. Information geometry on the curved q-exponential family with application to survival data analysis[J]. Physica A: Statistical Mechanics and its Applications, 2018, 512: 788–802. doi: 10.1016/j.physa.2018.08.143 TRANSTRUM M K, SARIĆ A T, and STANKOVIĆ A M. Information geometry approach to verification of dynamic models in power systems[J]. IEEE Transactions on Power Systems, 2018, 33(1): 440–450. doi: 10.1109/TPWRS.2017.2692523 HIAI F and PETZ D. Riemannian metrics on positive definite matrices related to means. II[J]. Linear Algebra and Its Applications, 2012, 436(7): 2117–2136. doi: 10.1016/j.laa.2011.10.029 刘俊凯, 王雪松, 王涛, 等. 信息几何在脉冲多普勒雷达目标检测中的应用[J]. 国防科技大学学报, 2011, 33(2): 77–80. doi: 10.3969/j.issn.1001-2486.2011.02.018LIU Junkai, WANG Xuesong, WANG Tao, et al. Application of information geometry to target detection for pulsed-Doppler radar[J]. Journal of National University of Defense Technology, 2011, 33(2): 77–80. doi: 10.3969/j.issn.1001-2486.2011.02.018 STEIN C. Inadmissibility of the usual estimator for the mean of a multivariate normal distribution[C]. The Third Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, USA, 1956: 197–206. HUA Xiaoqiang, CHENG Yongqiang, WANG Hongqiang, et al. Geometric means and medians with applications to target detection[J]. IET Signal Processing, 2017, 11(6): 711–720. doi: 10.1049/iet-spr.2016.0547 LENGLET C, ROUSSON M, DERICHE R, et al. Statistics on the manifold of multivariate normal distributions: theory and application to diffusion tensor MRI processing[J]. Journal of Mathematical Imaging and Vision, 2006, 25(3): 423–444. doi: 10.1007/s10851-006-6897-z -





 下载:
下载:
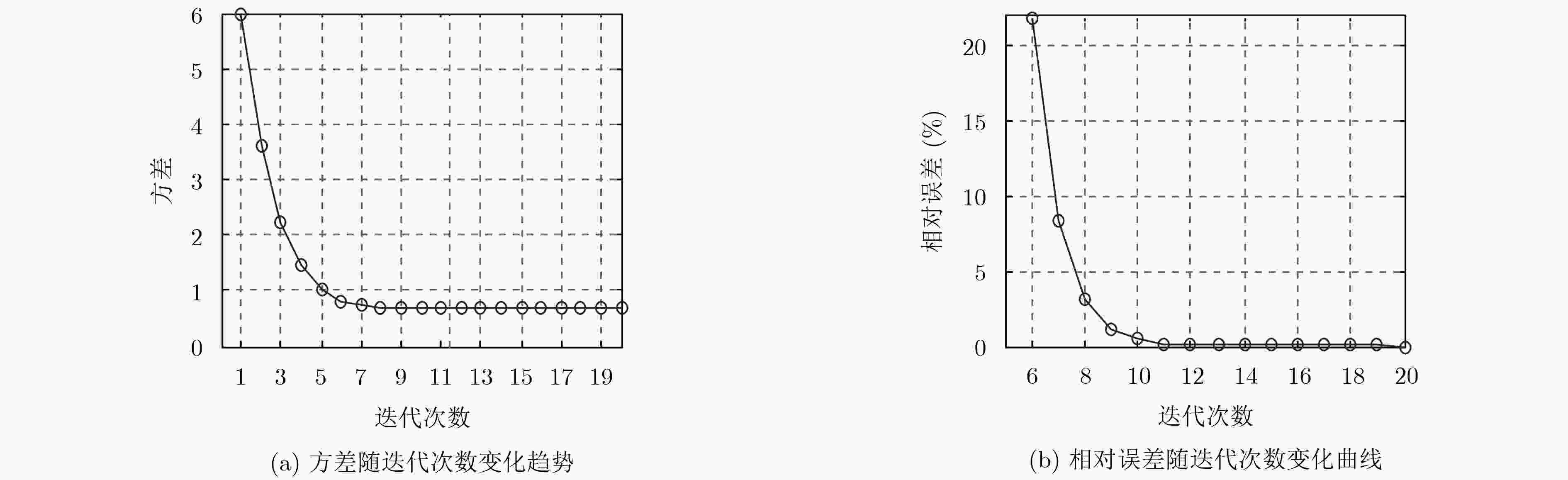
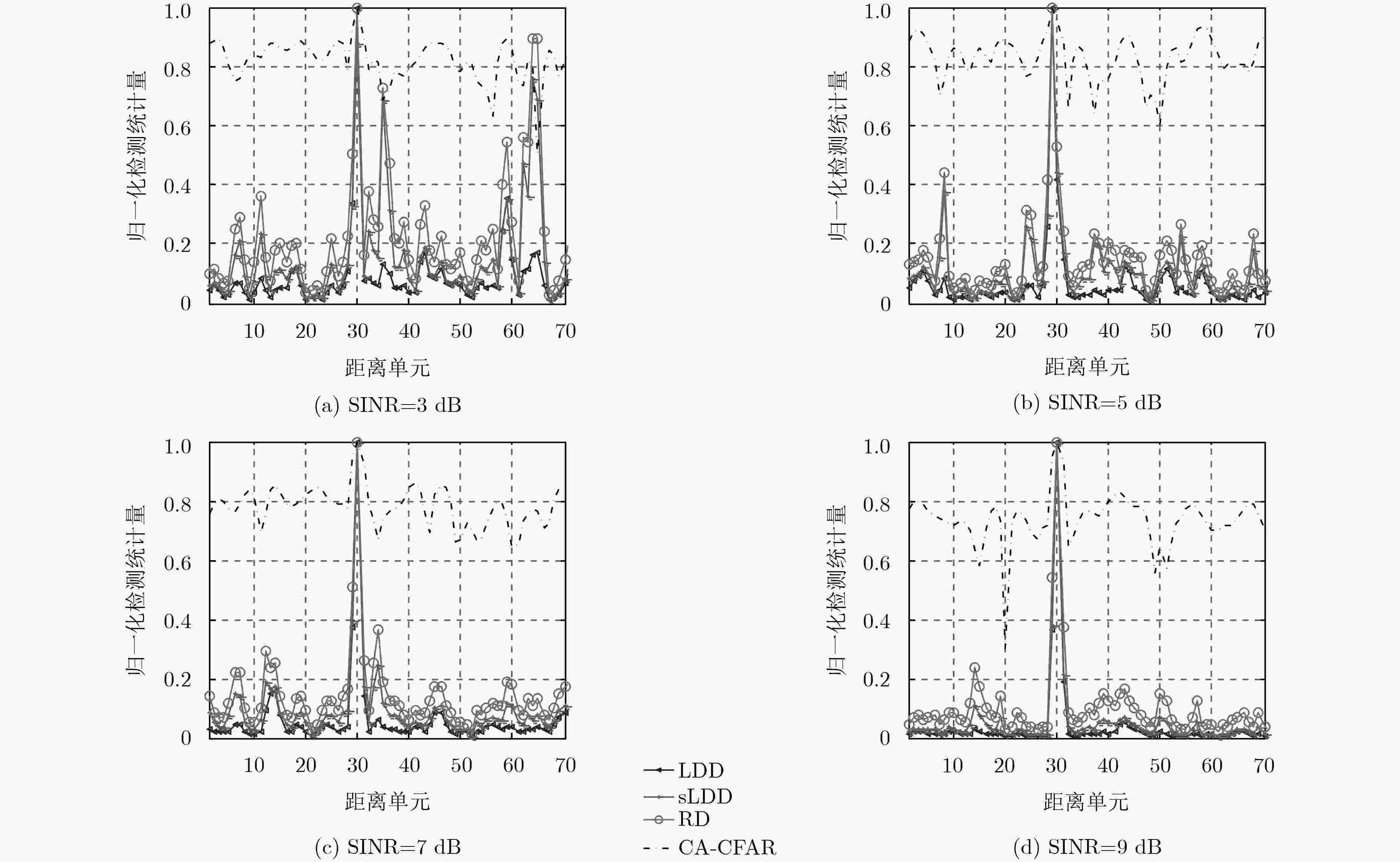
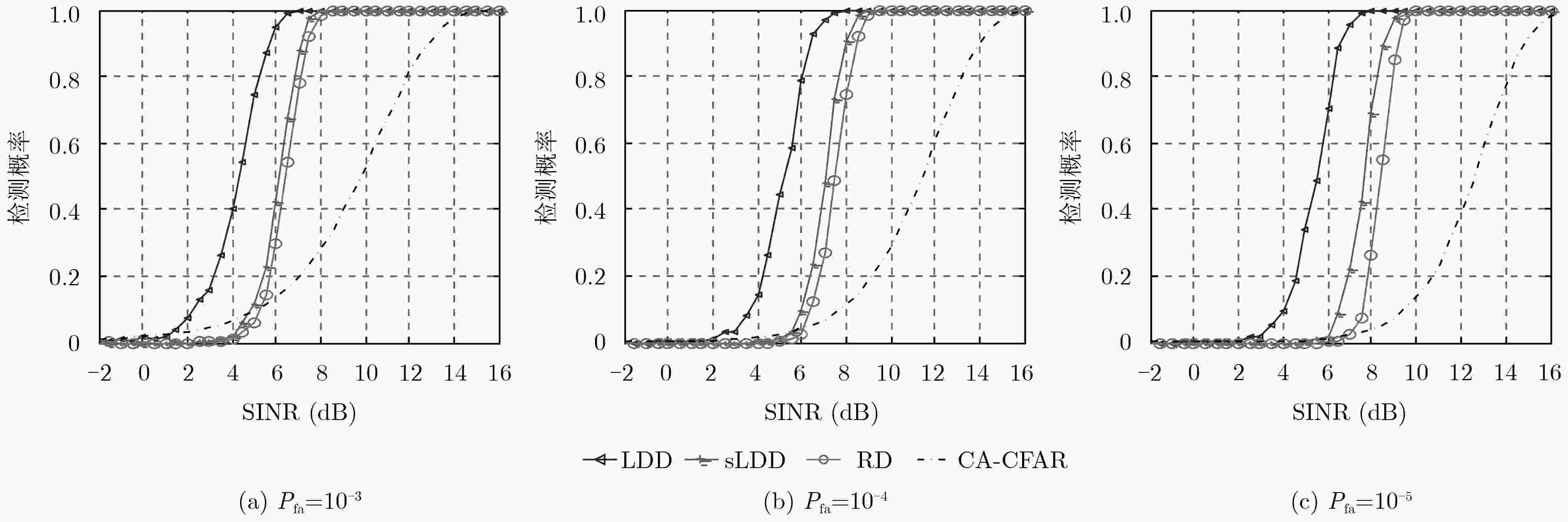


 下载:
下载:
