Automatic Rank Estimation Based Riemannian Optimization Matrix Completion Algorithm and Application to Image Completion
-
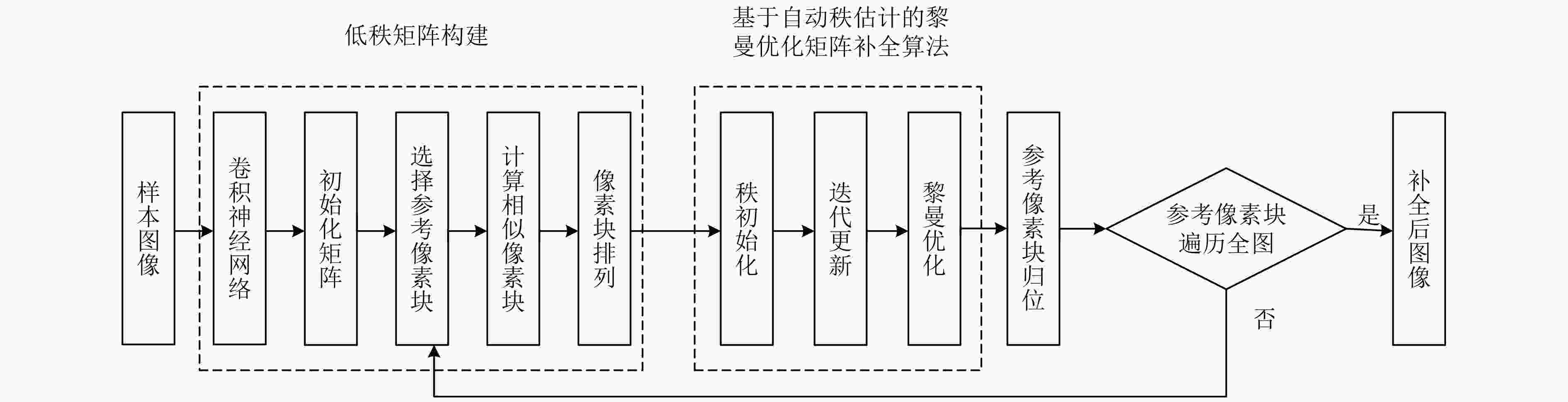
摘要: 矩阵补全(MC)作为压缩感知(CS)的推广,已广泛应用于不同领域。近年来,基于黎曼优化的MC算法因重构精度高、计算速度快的特点,引起了广泛关注。针对基于黎曼优化的MC算法需假设原矩阵秩固定已知,且随机选择迭代起点的特点,该文提出一种基于自动秩估计的黎曼优化MC算法。该算法通过优化包含秩正则项的目标函数,迭代获取秩估计值和预重构矩阵。在估计所得秩对应的矩阵空间上以预重构矩阵为迭代起点,利用基于黎曼流形的共轭梯度法进行矩阵补全,从而提高重构精度。实验结果表明,与几种经典的图像补全方法相比,该文算法图像重构精度显著提高。Abstract: As an extension of Compressed Sensing(CS), Matrix Completion(MC) is widely applied to different fields. Recently, the Riemannian optimization based MC algorithm attracts a lot of attention from researchers due to its high accuracy in reconstruction and computational efficiency. Considering that the Riemannian optimization based MC algorithm assumes a fixed rank of the original matrix, and selects a random initial point for iteration, a novel algorithm is proposed, namely automatic rank estimation based Riemannian optimization matrix completion algorithm. In the proposed algorithm, the estimate of rank is obtained minimizing the objective function that involving the rank regulation, in addition, the iterative starting point is optimized based on Riemannian manifold. The Riemannian manifold based conjugate gradient method is then used to complete the matrix, thereby improving the reconstruction precision. The experimental results demonstrate that the image completion performance is significantly improved using the proposed algorithm, compared with several classical image completion methods.
-
表 1 自动秩估计算法伪代码
算法1 自动秩估计算法 输入:${\text{A}} = {{\text{A}}_p} \in {\mathbb {R}^{m \times n}}$,索引矩阵${\text{Ω}}$,正则项系数$\mu $, $\alpha $,初始秩$\hat k$,最大迭代次数$K$,容错度${\tau _2}$。 初始化:执行奇异值分解${\text{A}}{\rm{ = }}{\text{U}}{\text{W}}{{\text{V}}^{\rm{T}}}$,将${\text{U}}$的第$r$列单位化记为${{\text{u}}_r}$,将${\text{V}}$的第$r$行单位化记为${{\text{v}}_r}$, ${\text{w}} = \left\{ {{w_r}} \right\}_{r = 1}^{\min \left( {m,n} \right)}$为${\text{W}}$中奇异值组成的 向量。令${\text{Z}} = {\text{0}}$, ${{\text{P}}_{{\Omega ^c}}}\left( {\text{A}} \right) = {\text{0}}$。 输出:${\text{Z}} $, $k$。 (1) for $i = 1,2,·\!·\!·,K$ do: (2) ${{\text{A}}_r} = {\text{A}}$; (3) 更新${{\text{u}}_r}$, ${{\text{v}}_r}$, ${w_r}$: for $r = 1,2, ·\!·\!· ,\hat k$ do: 若${w_r} \ne 0$,根据式(8)、式(9)和式(11)依次更新${{\text{u}}_r}$, ${{\text{v}}_r}$, ${w_r}$, ${{\text{A}}_r} = {{\text{A}}_r} - {w_r}{{\text{u}}_r}{\text{v}}_r^{\rm{T}}$, end; (4) 更新${\text{A}}$:更新${\text{Z}} = {\text{A}} - {{\text{A}}_r}$,令${ {\text{P} }_{ {\varOmega ^c} } }\left( {\text{A} } \right) = { {\text{P} }_{ {\varOmega ^c} } }\left( {\text{Z} } \right)$; (5) 更新$k$:for $k = 1,2, ·\!·\!· ,\min\left( {m,n} \right)$ do: 计算$f\left( k \right) = {\rm{ } }\mu \left| { { {\text{w} }_r} } \right|_{r = 1}^k + 0.5\parallel {\text{A} } - \sum\limits_{r = 1}^k { {w_r}{ {\text{u} }_r}{ {\text{v} }_r}^{\rm{T} } } \parallel _{\rm F}^2 + \alpha k$,若$f\left( k \right) < f\left( {k + 1} \right)$,则结束循环, end; (6) $\hat k = k$; (7) 若${{\parallel {{\text{P}}_\Omega }\left( {{\text{A}} - {\text{Z}}} \right){\parallel _{\rm{F}}}} /{\parallel {{\text{P}}_\Omega }\left( {\text{A}} \right){\parallel _{\rm{F}}}}} < {\tau _2}$或${{\parallel {{\text{A}}^{i + 1}} - {{\text{A}}^i}{\parallel _{\rm{F}}}} / {\parallel {{\text{A}}^{i + 1}}{\parallel _{\rm{F}}}}} < {\tau _2}$,则结束循环; (8) end。 表 2 基于自动秩估计的黎曼优化矩阵补全算法伪代码
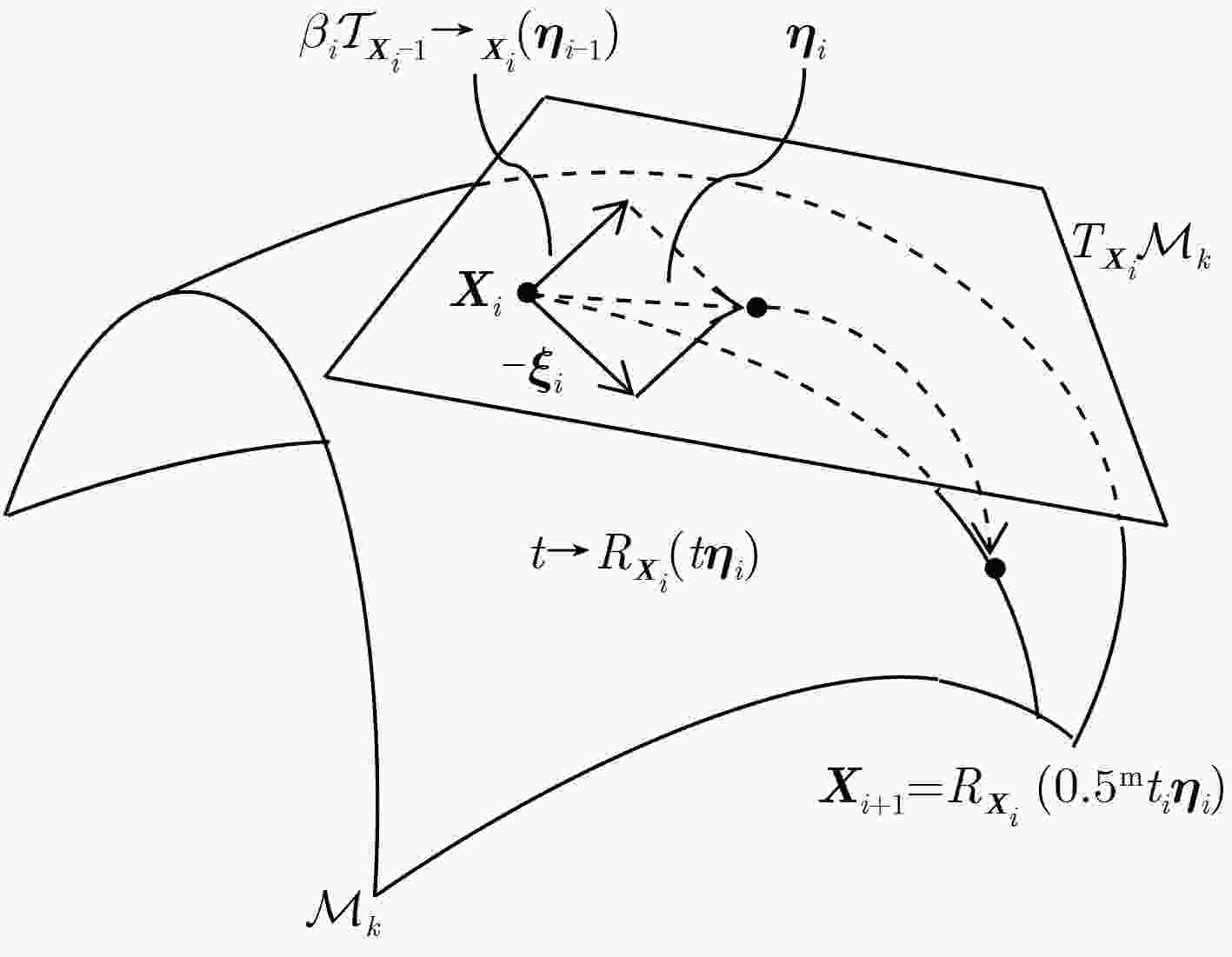
算法2 基于自动秩估计的黎曼优化矩阵补全算法 输入:${{\text{X}} _1}{\rm{ = }}Z \in {{\cal M}_k}$(${\text{Z}} $和$k$源于算法1),容错度${\tau _1}$,切向量${{\text{η}} _0}{\rm{ = }}0$。 输出:${{\text{X}}^ * }$。 (1) for $i = 1,2, ·\!·\!· ,K$ do: (2) 梯度${\xi _i}: = {\rm{gradf}}\left( {{{\text{X}}_i}} \right)$; % 计算黎曼梯度 (3) 若$\parallel {\xi _i}\parallel \le {\tau _1}$,则停止迭代,令${{\text{X}}^ * }{\rm{ = }}{{\text{X}}_i}$,否则转(4);% 终止条件 (4) 共轭方向${{\text{η}} _i}: = - {\xi _i} + {\beta _i}{{\cal T}_{{{\text{X}} _{i - 1}} \to {{\text{X}}_i}}}\left( {{{\text{η}}_{i - 1}}} \right)$; % 计算共轭方向 (5) 步长${t_i} = {{\rm{argmin}}_t}f\left( {{{\text{X}}_i} + t{{\text{η}} _i}} \right)$; % 计算步长 (6) 执行Armijo回溯以找到满足$f\left( {{{\text{X}}_i}} \right) - f\left( {{R_{{{\text{X}}_i}}}\left( {0.{5^m}{t_i}{{\text{η}} _i}} \right)} \right) \ge - 0.0001 \times 0.{5^m}{t_i}\left\langle {{\xi _i},{{\text{η}} _i}} \right\rangle $且m≥0的最小整数,计算${X_{i + 1}}: = {R_{{{\text{X}}_i}}}\left( {0.{5^m}{t_i}{{\text{η}} _i}} \right)$; % 收缩算子 (7) end。 表 3 基于各算法的补全后图像PSNR(dB)/SSIM指标评价
采样率(%) 图像补全算法 本文算法 SVP OptSpace SVT IALM 10 Barbara 25.1371/0.1018 27.1138/0.0749 28.4540/0.2703 26.4330/0.1817 27.9684/0.2217 House 25.0207/0.0737 27.0100/0.0845 28.8611/0.3805 26.0756/0.2122 27.3161/0.0319 20 Barbara 29.5855/0.6187 29.4788/0.3705 29.0277/0.3509 27.7929/0.3638 29.0097/0.3175 House 32.1346/0.7750 30.5881/0.4681 29.2989/0.4096 28.0950/0.4569 29.1008/0.0667 30 Barbara 31.8223/0.7775 30.5821/0.5530 29.7224/0.4138 29.0192/0.5193 29.6337/0.4010 House 34.3279/0.8434 32.6125/0.6858 29.8818/0.4437 30.2986/0.6472 29.9081/0.4560 40 Barbara 33.1805/0.8054 31.3704/0.6249 30.4532/0.4922 30.2063/0.6471 30.2152/0.4592 House 36.9926/0.9175 33.4685/0.7449 30.5393/0.4687 32.2618/0.7718 30.6276/0.4546 50 Barbara 34.3090/0.8545 32.3230/0.7045 31.1457/0.5349 31.6388/0.7607 31.0285/0.5060 House 37.9729/0.9342 34.4193/0.7909 31.8817/0.5854 34.2940/0.8575 31.3316/0.4965 60 Barbara 35.5808/0.8932 33.3609/0.7612 32.2731/0.5955 33.4085/0.8552 31.9375/0.5660 House 39.5723/0.9504 35.5242/0.8297 33.5629/0.7099 36.5579/0.9150 32.3391/0.4992 70 Barbara 37.1206/0.9277 34.6884/0.8124 33.4690/0.6453 35.7766/0.9191 33.0595/0.6449 House 41.0744/0.9622 36.8819/0.8690 34.4479/0.7395 39.3028/0.9524 33.4229/0.5724 80 Barbara 39.0801/0.9529 36.4704/0.8665 35.3219/0.7479 38.8081/0.9565 34.7671/0.6462 House 43.1665/0.9728 38.6710/0.9042 37.2815/0.8288 41.8076/0.9234 35.2485/0.6317 90 Barbara 42.3685/0.9699 39.3773/0.9213 38.4127/0.8653 40.6578/0.9357 38.0598/0.7796 House 46.1068/0.9810 41.9691/0.9442 40.3322/0.8943 42.0364/0.9707 38.1441/0.7449 -
臧芳. 一种利用低秩矩阵填充技术恢复气象数据的方法[J]. 计算机应用与软件, 2017, 34(9): 322–327. doi: 10.3969/j.issn.1000-386x.2017.09.063ZANG Fang. Method of restoring meteorological data using low-rank matrix filling technique[J]. Computer Applications and Software, 2017, 34(9): 322–327. doi: 10.3969/j.issn.1000-386x.2017.09.063 杨国亮, 鲁海荣, 丰义琴, 等. 基于非局部矩阵填充的文物修复技术研究[J]. 计算机应用与软件, 2016, 33(11): 126–129. doi: 10.3969/j.issn.1000-386x.2016.11.030YANG Guoliang, LU Hairong, FENG Yiqin, et al. On cultural relic images restoration technology based on non-local matrix completion[J]. Computer Applications and Software, 2016, 33(11): 126–129. doi: 10.3969/j.issn.1000-386x.2016.11.030 陈秋实, 杨强, 董英凝, 等. 基于矩阵填充的合成宽带高频雷达非网格目标分辨技术研究[J]. 电子与信息学报, 2017, 39(12): 2874–2880. doi: 10.11999/JEIT170449CHEN Qiushi, YANG Qiang, DONG Yingning, et al. Off-the-grid targets resolution of synthetic bandwidth high frequency radar based on matrix completion[J]. Journal of Electronics &Information Technology, 2017, 39(12): 2874–2880. doi: 10.11999/JEIT170449 CAI T T and ZHANG Anru. Sparse representation of a polytope and recovery of sparse signals and low-rank matrices[J]. IEEE Transactions on Information Theory, 2014, 60(1): 122–132. doi: 10.1109/TIT.2013.2288639 CAI Jianfeng, CANDES E J, and SHEN Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956–1982. doi: 10.1137/080738970 LIN Zhouchen, CHEN Minming, and MA Yi. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. arXiv preprint arXiv: 1009.5055, 2010. VANDEREYCKEN B. Low-rank matrix completion by riemannian optimization[J]. SIAM Journal on Optimization, 2013, 23(2): 1214–1236. doi: 10.1137/110845768 MEKA R, JAIN P, and DHILLON I S. Guaranteed rank minimization via singular value projection[C]. Proceedings of the Neural Information Processing Systems Conference, Vancouver, Canada, 2010: 937–945. KESHAVAN R H and OH S. A gradient descent algorithm on the grassman manifold for matrix completion[J]. arXiv preprint arXiv: 0910.5260, 2009. SHI Qiquan, LU Haiping, and CHEUNG Y. Rank-one matrix completion with automatic rank estimation via L1-norm regularization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4744–4757. doi: 10.1109/TNNLS.2017.2766160 陈蕾, 陈松灿. 矩阵补全模型及其算法研究综述[J]. 软件学报, 2017, 28(6): 1547–1564. doi: 10.13328/j.cnki.jos.005260CHEN Lei and CHEN Songcan. Survey on matrix completion models and algorithms[J]. Journal of Software, 2017, 28(6): 1547–1564. doi: 10.13328/j.cnki.jos.005260 CANDÈS E J and RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717–772. doi: 10.1007/s10208-009-9045-5 LI Wei, ZHAO Lei, LIN Zhijie, et al. Non-local image inpainting using low‐rank matrix completion[J]. Computer Graphics Forum, 2015, 34(6): 111–122. doi: 10.1111/cgf.12521 LIU Ping, LEWIS J, and RHEE T. Low-rank matrix completion to reconstruct incomplete rendering images[J]. IEEE Transactions on Visualization and Computer Graphics, 2018, 24(8): 2353–2365. doi: 10.1109/TVCG.2017.2722414 DONG Bin, MAO Yu, OSHER S, et al. Fast linearized Bregman iteration for compressive sensing and sparse denoising[J]. Communications in Mathematical Sciences, 2010, 8(1): 93–111. doi: 10.4310/CMS.2010.v8.n1.a6 LIU Yuanyuan, SHANG Fanhua, WEI Fan, et al. Generalized higher-order orthogonal iteration for tensor decomposition and completion[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 1763–1771. HORE A and ZIOU D. Image quality metrics: PSNR vs. SSIM[C]. Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 2010: 2366–2369. ÖZIÇ M Ü and ÖZŞEN S. A new model to determine asymmetry coefficients on MR images using PSNR and SSIM[C]. Proceedings of 2017 International Artificial Intelligence and Data Processing Symposium, Malatya, Turkey, 2017: 1–6. -





 下载:
下载:




 下载:
下载:
