Multi-channel SAR-GMTI Clutter Suppression Method Based onHypersonic Platform Forward Squint
-
摘要:
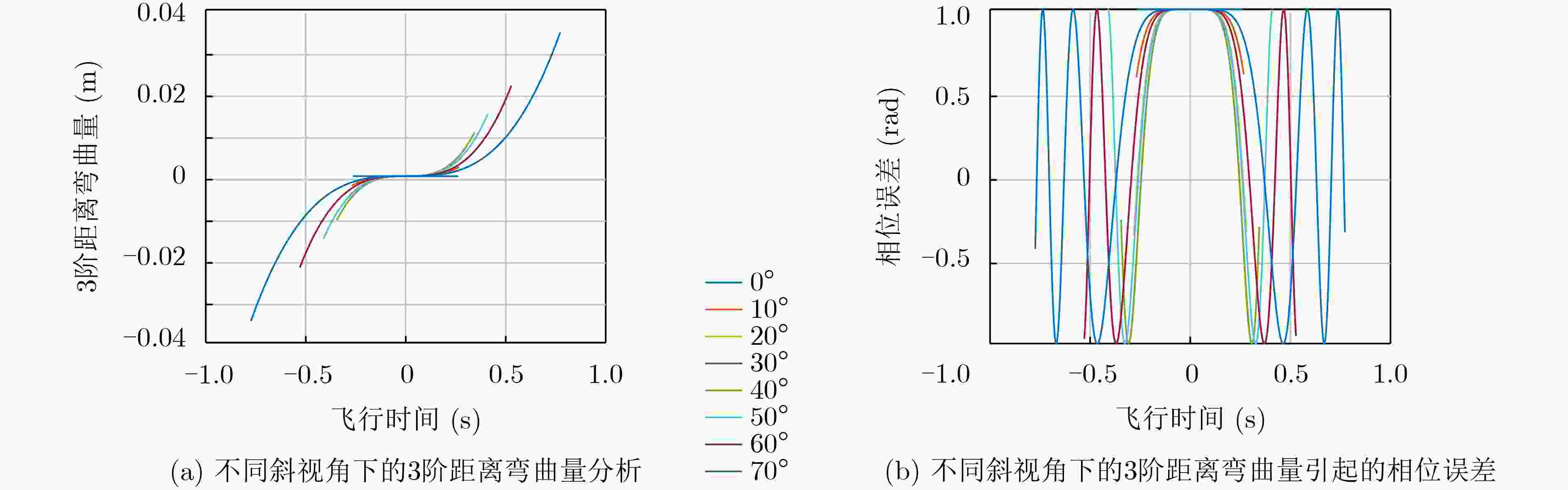
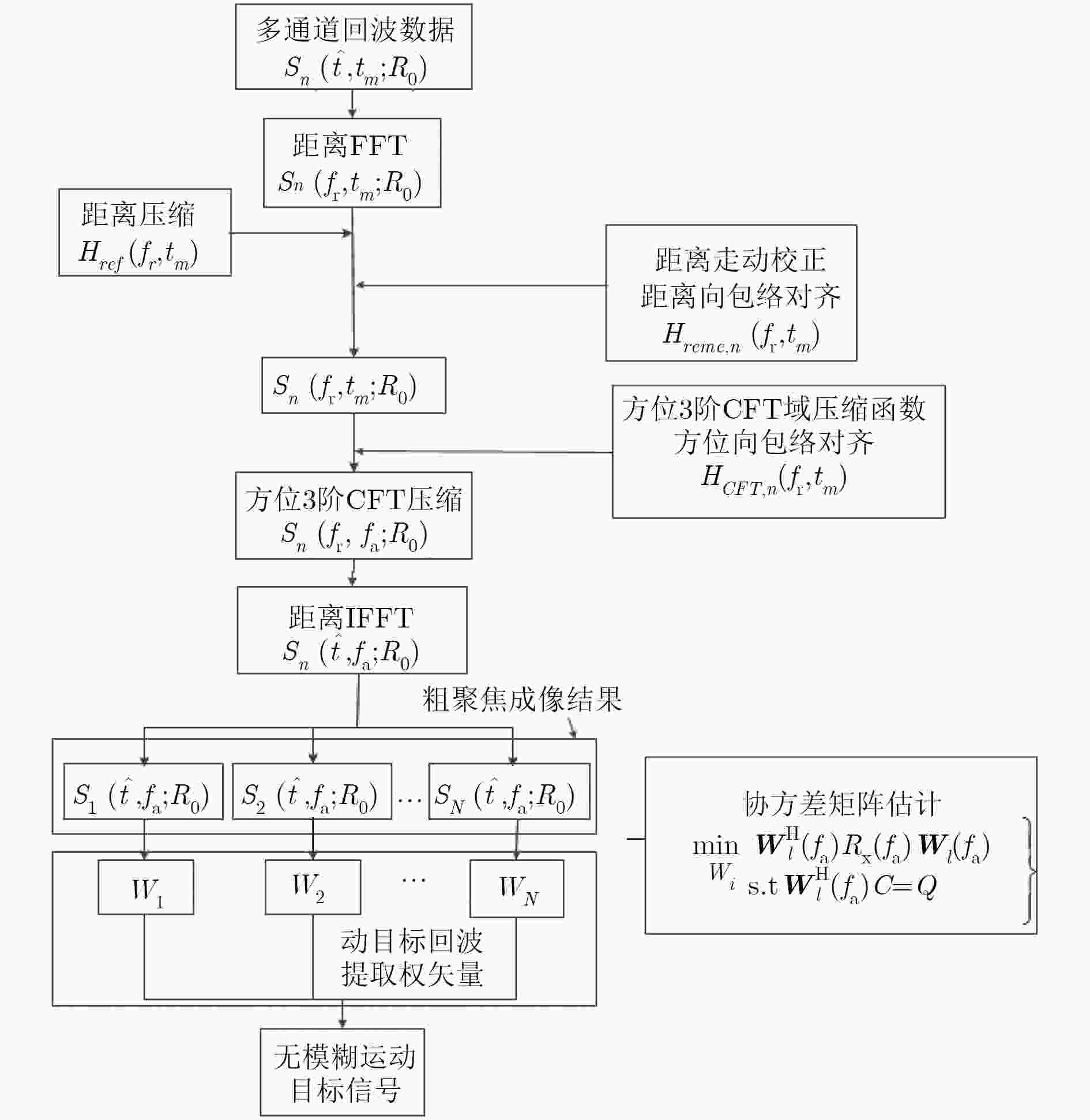
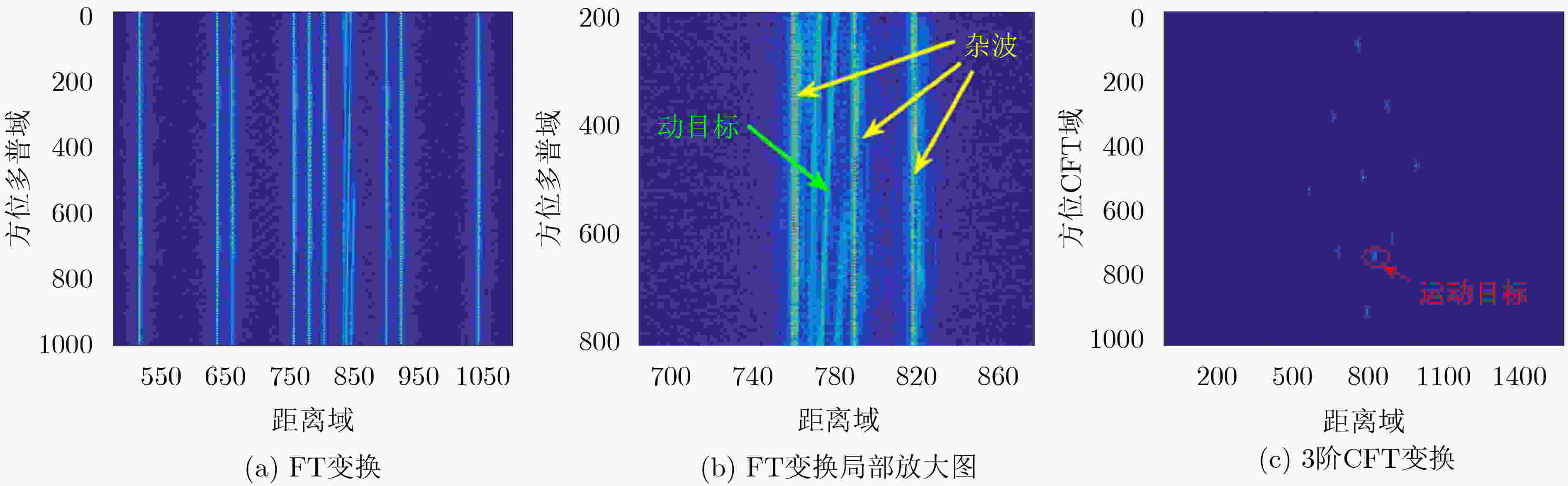
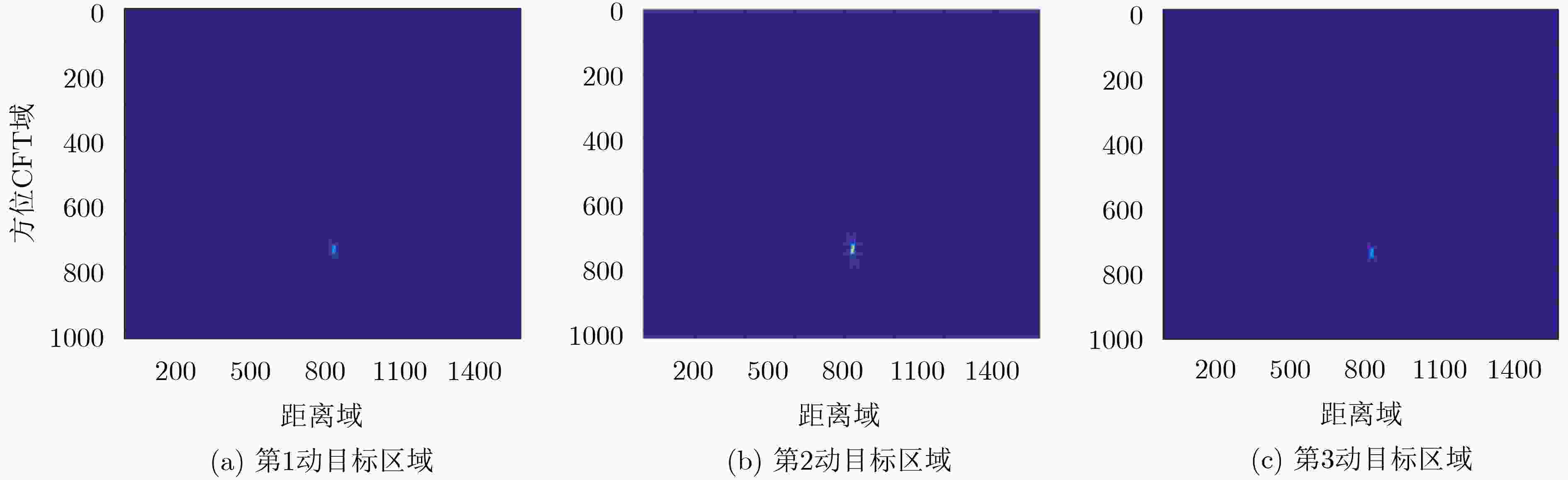
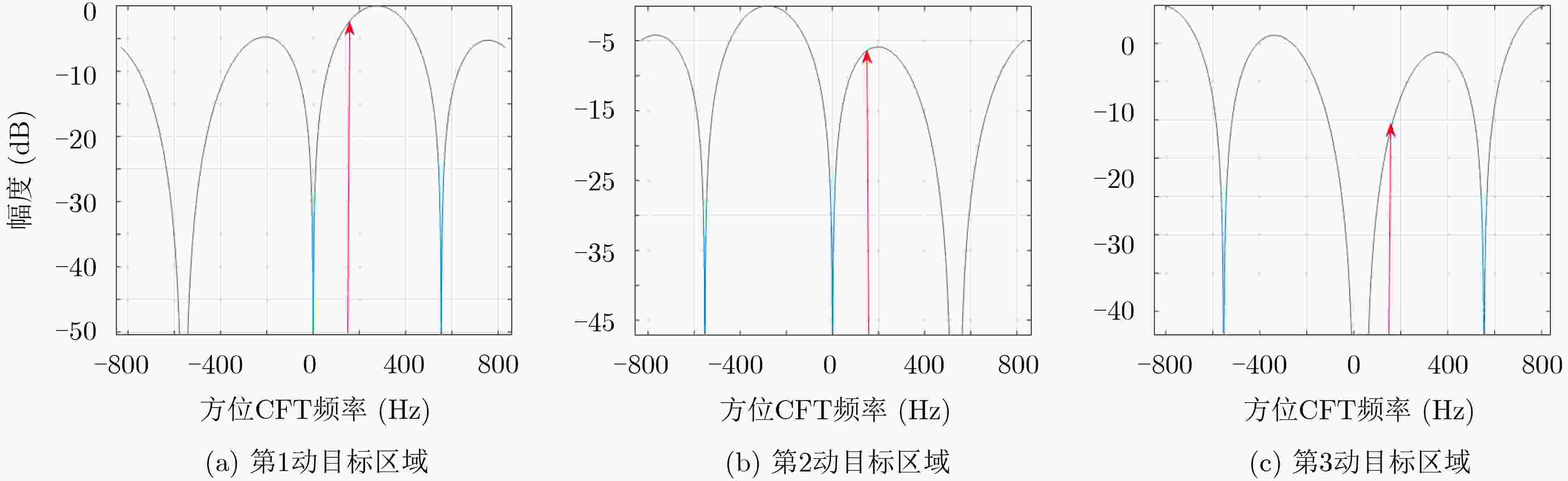
针对高超声速(HSV)平台雷达系统,该文提出一种基于高超声速平台前斜视多通道合成孔径雷达地面动目标检测(SAR-GMTI)杂波抑制方法。该方法先进行时域距离走动校正和距离压缩,并补偿距离向通道相位误差实现距离向包络对齐;然后再对方位多普勒扩展的信号进行3阶线调频傅里叶变换(CFT)压缩,并补偿方位向通道相位误差实现方位向包络对齐;接着在距离时域-方位CFT域利用数字波束形成(DBF)技术对杂波及其模糊分量置零进行空时自适应处理(STAP),从而可以有效抑制静止杂波及其模糊分量并提取出无模糊的运动目标回波信号。
-
关键词:
- 合成孔径雷达地面动目标检测 /
- 高超声速飞行器 /
- 前斜视 /
- 多普勒模糊 /
- 空时自适应处理
Abstract:According to the HyperSonic Vehicle (HSV) borne radar platform system, a multi-channel SAR-GMTI clutter suppression method is presented based on hypersonic platform forward squint mode. First, range walk correction and range compression are completed in the time domain, and the distance envelope is aligned simultaneously with phase error compensation. Then, the Doppler extended signal is compressed by three-order azimuth Chirp Fourier Transform (CFT), and the azimuth envelope of the echo is aligned with phase error compensation simultaneously. Next, the Digital Beam Forming (DBF) technology is applied to the range time-azimuth CFT domain by nulling the clutter and its ambiguous components to achieve Space-Time Adaptive Processing (STAP). The stationary clutter and its ambiguous components can be suppressed effectively and the echo signs of the moving target without blurring can be extracted.
-
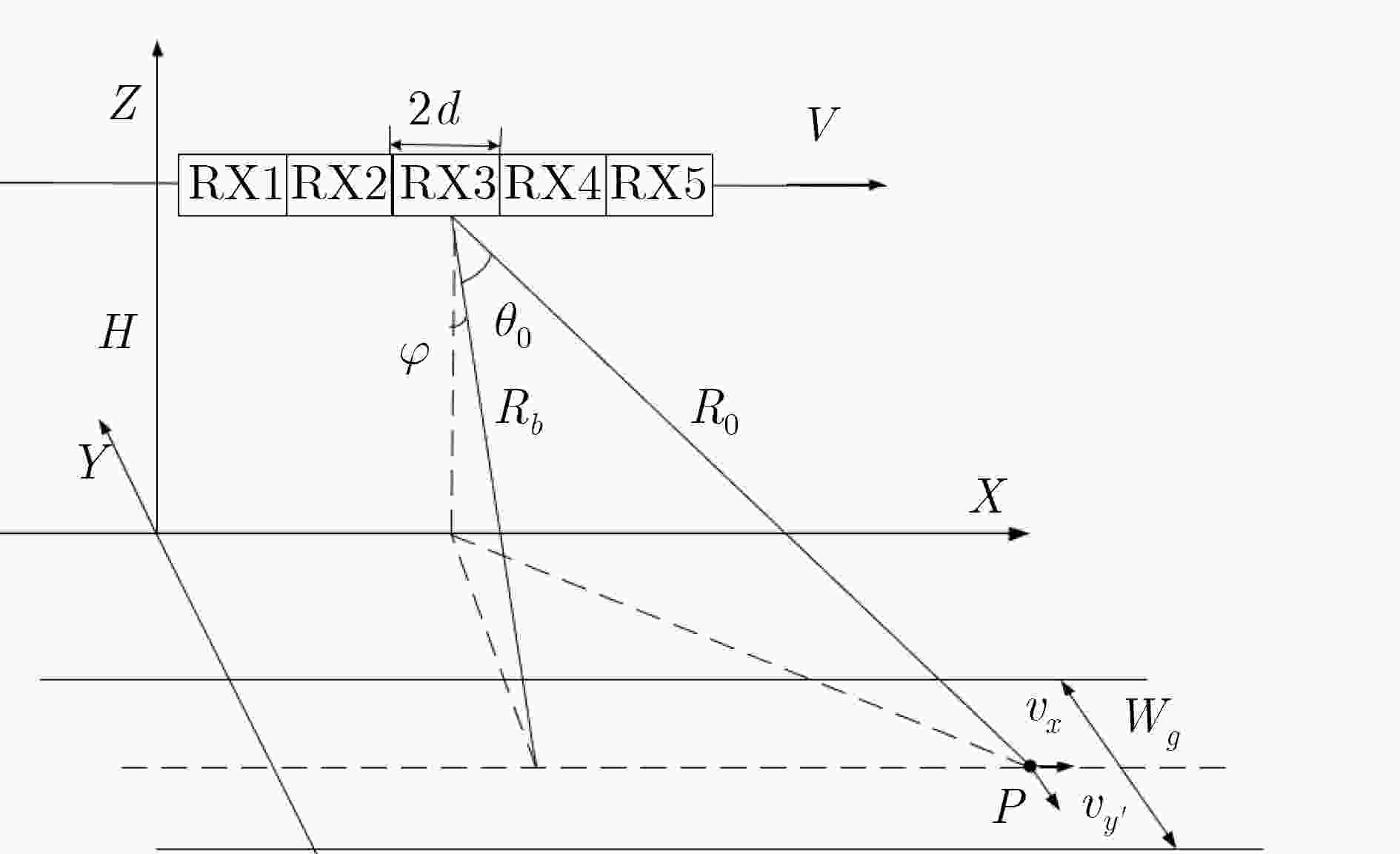
表 1 仿真参数
参数名称 载频${f_{\rm{c}}}$ 斜视角 平台高度H 中心斜距R 距离分辨率 信号多普勒带宽 重频PRF 平台速度V 相邻通道间距d 方位分辨率 参数值 10 GHz 50° 30 km 60 km 1 m 1530 Hz 554 Hz 2380 m/s 1.5 m 1 m -
WANG Wenqin. Near-space vehicle-borne SAR with reflector antenna for high-resolution and wide-swath remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 338–348. doi: 10.1109/TGRS.2011.2158224 XU Gang, XING Mengdao, ZHANG Lei, et al. Robust autofocusing approach for highly squinted SAR imagery using the extended wavenumber algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(10): 5031–5046. doi: 10.1109/TGRS.2013.2276112 XU Huajian, YANG Zhiwei, TIAN Min, et al. An extended moving target detection approach for high-resolution multichannel SAR-GMTI systems based on enhanced shadow-aided decision[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(2): 715–729. doi: 10.1109/TGRS.2017.2754098 WANG Yu, CAO Yunhe, PENG Zhigang, et al. Clutter suppression and GMTI for hypersonic vehicle borne SAR system with MIMO antenna[J]. IET Signal Processing, 2017, 11(8): 909–915. doi: 10.1049/iet-spr.2017.0193 XU Jia, HUANG Zuzhen, WANG Zhirui, et al. Radial velocity retrieval for multichannel SAR moving targets with time-space Doppler deambiguity[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 35–48. doi: 10.1109/TGRS.2017.2720692 HUANG Yan, LIAO Guisheng, XU Jingwei, et al. GMTI and parameter estimation for MIMO SAR system via fast interferometry RPCA method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(3): 1774–1787. doi: 10.1109/TGRS.2017.2768243 WANG Guanqiong, LI Jingwen, and WEI Yang. Influence factors analysis of SAR-GMTI system performance[J]. Applied Mechanics and Materials, 2013, 380-384: 692–696. doi: 10.4028/www.scientific.net/AMM.380-384.692 YANG Taoli, WANG Yong, and LI Wei. A moving target imaging algorithm for HRWS SAR/GMTI systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1147–1157. doi: 10.1109/TAES.2017.2667858 邢孟道, 孙光才, 李学仕. 用于高分辨率宽测绘带SAR系统的SAR/GMTI处理方法研究[J]. 雷达学报, 2015, 4(4): 375–385. doi: 10.12000/JR15096XING Mengdao, SUN Guangcai, and LI Xueshi. Study on SAR/GMTI processing for high-resolution wide-swath SAR system[J]. Journal of Radars, 2015, 4(4): 375–385. doi: 10.12000/JR15096 吴明宇, 杨桃丽, 吴顺君, 等. 星载多通道高分辨率宽测绘带SAR系统运动目标检测方法[J]. 电子与信息学报, 2014, 36(2): 441–444. doi: 10.3724/SP.J.1146.2013.00465WU Mingyu, YANG Taoli, WU Shunjun, et al. Ground moving target indication for spaceborne multi-channel high resolution wide swath SAR system[J]. Journal of Electronics &Information Technology, 2014, 36(2): 441–444. doi: 10.3724/SP.J.1146.2013.00465 XIA Xianggen. Discrete chirp-Fourier transform and its application to chirp rate estimation[J]. IEEE Transactions on Signal Processing, 2000, 48(11): 3122–3133. doi: 10.1109/78.875469 XIA Meng and YANG Xiaoniu. Moving target parameter estimation of spaceborne SAR-GMTI based on the analysis of acceleration[C]. 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 1242–1246. doi: 10.1109/CIE-Radar.2011.6159781. SUWA K, YAMAMOTO K, TSUCHIDA M, et al. Image-based target detection and radial velocity estimation methods for multichannel SAR-GMTI[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(3): 1325–1338. doi: 10.1109/TGRS.2016.2622712 -





 下载:
下载:


 下载:
下载:
