JPEG Compression Artifacts Reduction Algorithm Based on Multi-scale Dense Residual Network
-
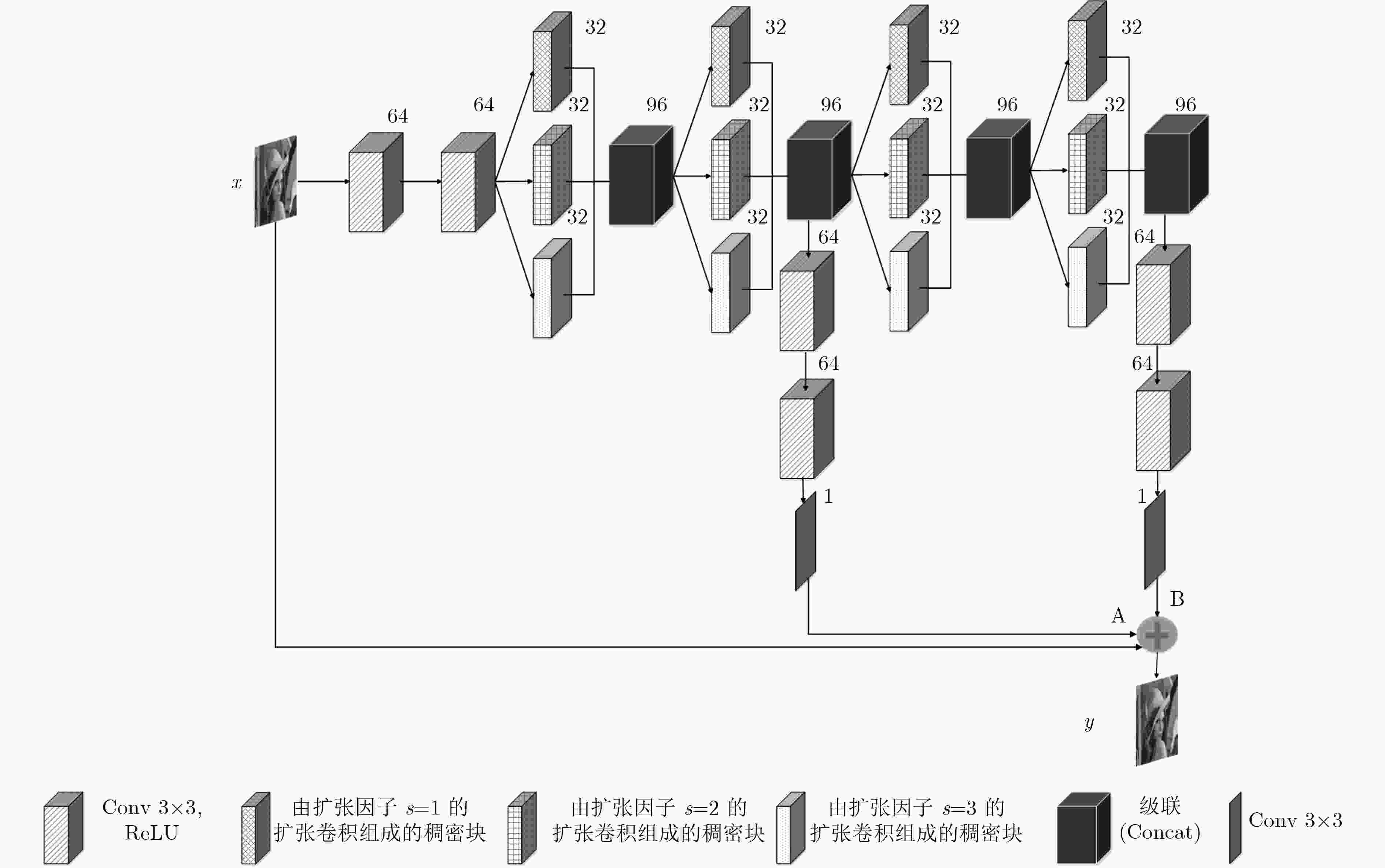
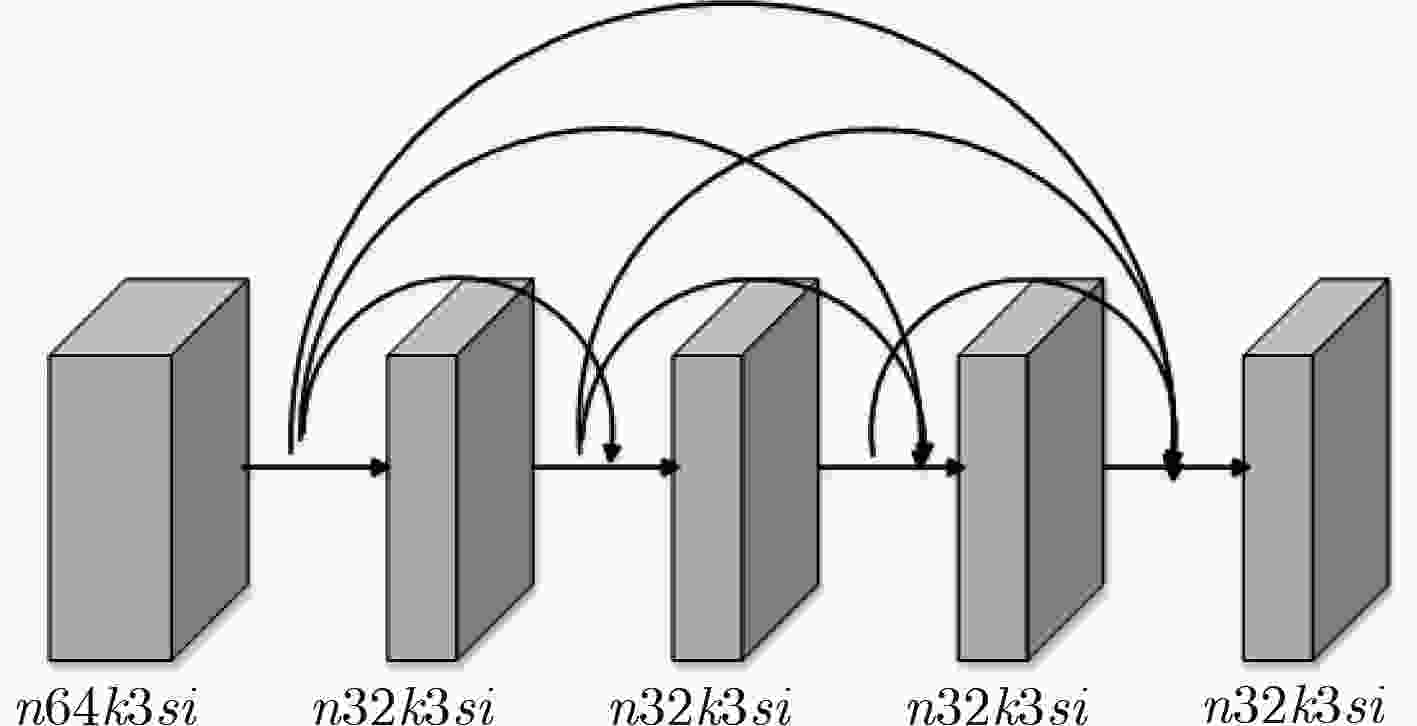
摘要: JPEG在高压缩比的情况下,解压缩后的图像会产生块效应、边缘振荡效应和模糊,严重影响了图像的视觉效果。为了去除JPEG压缩伪迹,该文提出了多尺度稠密残差网络。首先把扩张卷积引入到残差网络的稠密块中,利用不同的扩张因子,使其形成多尺度稠密块;然后采用4个多尺度稠密块将网络设计成包含2条支路的结构,其中后一条支路用于补充前一条支路没有提取到的特征;最后采用残差学习的方法来提高网络的性能。为了提高网络的通用性,采用具有不同压缩质量因子的联合训练方式对网络进行训练,针对不同压缩质量因子训练出一个通用模型。经实验表明,该文方法不仅具有较高的JPEG压缩伪迹去除性能,且具有较强的泛化能力。Abstract: In the case of high compression rates, the JPEG decompressed image can produce blocking artifacts, ringing effects and blurring, which affect seriously the visual effect of the image. In order to remove JPEG compression artifacts, a multi-scale dense residual network is proposed. Firstly, the proposed network introduces the dilate convolution into a dense block and uses different dilation factors to form multi-scale dense blocks. Then, the proposed network uses four multi-scale dense blocks to design the network into a structure with two branches, and the latter branch is used to supplement the features that are not extracted by the previous branch. Finally, the proposed network uses residual learning to improve network performance. In order to improve the versatility of the network, the network is trained by a joint training method with different compression quality factors, and a general model is trained for different compression quality factors. Experiments demonstrate that the proposed algorithm not only has high JPEG compression artifacts reduction performance, but also has strong generalization ability.
-
Key words:
- JPEG compression /
- Compression artifacts /
- Multi-scale dense blocks /
- Dilate convolution
-
表 1 ARCNN的4个模型在LIVE1数据集上的PSNR(dB)对比
模型 QF 10 20 30 40 JPEG 27.77 30.07 31.41 32.35 ARCNN(${\rm{QF}} = 10$) 28.96 30.79 31.51 31.90 ARCNN(${\rm{QF}} = 20$) 28.78 31.30 32.53 33.30 ARCNN(${\rm{QF}} = 30$) 28.60 31.25 32.69 33.61 ARCNN(${\rm{QF}} = 40$) 28.48 31.14 32.62 33.63 表 2 本文方法在LIVE1数据集上的PSNR(dB)/SSIM对比
方法 QF 10 20 30 40 JPEG 27.77/0.7905 30.07/0.8683 31.41/0.9000 32.35/0.9173 ARCNN 28.96/0.8217 31.30/0.8871 32.69/0.9161 33.63/0.9303 L4 Residual 29.08/0.8241 31.42/0.8900 32.80/0.9174 33.78/0.9322 L8 Residual – 31.51/0.8911 – – DnCNN-3 29.20/0.8262 31.59/0.8936 32.98/0.9204 33.96/0.9346 本文方法 29.49/0.8329 31.81/0.8952 33.08/0.9196 34.14/0.9367 表 3 本文方法在Classic5数据集上的PSNR(dB)/SSIM对比
方法 QF 10 20 30 40 JPEG 27.82/0.7800 30.12/0.8541 31.48/0.8844 32.43/0.9011 ARCNN 29.04/0.8108 31.16/0.8691 32.52/0.8963 33.34/0.9098 DnCNN-3 29.40/0.8201 31.63/0.8775 32.90/0.9011 33.77/0.9141 本文方法 29.68/0.8275 31.87/0.8798 33.03/0.9013 33.95/0.9166 表 4 本文方法在LIVE1数据集上的PSNR(dB)/SSIM对比
方法 QF 15 25 35 45 JPEG 29.13/0.8402 30.81/0.8869 31.93/0.9101 32.78/0.9241 DnCNN-3 30.61/0.8697 32.35/0.9094 33.53/0.9287 34.39/0.9400 本文方法 30.83/0.8733 32.50/0.9095 33.68/0.9303 34.56/0.9416 表 5 不同尺度的选择在LIVE1数据集上的PSNR(dB)/SSIM对比
不同尺度 QF 10 15 20 25 单一尺度($3 \times 3$) 29.42/0.8309 30.78/0.8719 31.75/0.8942 32.46/0.9086 单一尺度($5 \times 5$) 29.44/0.8316 30.79/0.8719 31.76/0.8945 32.46/0.9090 本文方法 29.49/0.8329 30.83/0.8733 31.81/0.8952 32.50/0.9095 表 6 不同网络层数在LIVE1数据集上的PSNR(dB)/SSIM对比
不同层数 QF 10 15 20 25 Dense3 29.45/0.8318 30.79/0.8714 31.77/0.8947 32.47/0.9090 Dense4 29.47/0.8325 30.81/0.8728 31.79/0.8950 32.49/0.9092 Dense5 29.49/0.8329 30.83/0.8733 31.81/0.8952 32.50/0.9095 Dense6 29.47/0.8324 30.81/0.8735 31.79/0.8951 32.49/0.9099 表 7 使用普通块和稠密块在LIVE1数据集上的PSNR(dB)/SSIM对比
方法 QF 10 15 20 25 普通块 29.39/0.8303 30.75/0.8712 31.71/0.8938 32.41/0.9081 稠密块 29.49/0.8329 30.83/0.8733 31.81/0.8952 32.50/0.9095 -
FOI A, KATKOVNIK V, and EGIAZARIAN K. Pointwise shape-adaptive DCT for high-quality denoising and deblocking of grayscale and color images[J]. IEEE Transactions on Image Processing, 2007, 16(5): 1395–1411. doi: 10.1109/TIP.2007.891788 YOO S B, CHOI K, and RA J B. Post-processing for blocking artifact reduction based on inter-block correlation[J]. IEEE Transactions on Multimedia, 2014, 16(6): 1536–1548. doi: 10.1109/TMM.2014.2327563 ZHAO Chen, ZHANG Jian, MA Siwei, et al. Reducing image compression artifacts by structural sparse representation and quantization constraint prior[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2017, 27(10): 2057–2071. doi: 10.1109/TCSVT.2016.2580399 吕晓琪, 吴凉, 谷宇, 等. 基于深度卷积神经网络的低剂量CT肺部去噪[J]. 电子与信息学报, 2018, 40(6): 1353–1359. doi: 10.11999/JEIT170769LÜ Xiaoqi, WU Liang, GU Yu, et al. Low dose CT lung denoising model based on deep convolution neural network[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1353–1359. doi: 10.11999/JEIT170769 DONG Chao, LOY C C, HE Kaiming, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295–307. doi: 10.1109/TPAMI.2015.2439281 郭智, 宋萍, 张义, 等. 基于深度卷积神经网络的遥感图像飞机目标检测方法[J]. 电子与信息学报, 2018, 40(11): 2684–2690. doi: 10.11999/JEIT180117GUO Zhi, SONG Ping, ZHANG Yi, et al. Aircraft detection method based on deep convolutional neural network for remote sensing images[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2684–2690. doi: 10.11999/JEIT180117 REN Shaoqing, HE Kaiming, GIRSHICK R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137–1149. doi: 10.1109/TPAMI.2016.2577031 BADRINARAYANAN V, KENDALL A, and CIPOLLA R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481–2495. doi: 10.1109/TPAMI.2016.2644615 DONG Chao, DENG Yubin, LOY C C, et al. Compression artifacts reduction by a deep convolutional network[C]. 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 2015: 576-584. doi: 10.1109/ICCV.2015.73. SVOBODA P, HRADIS M, BARINA D, et al. Compression artifacts removal using convolutional neural networks[J/OL]. arXiv preprint arXiv: 1605.00366. http://arxiv.org/abs/1605.00366, 2016. ZHANG Kai, ZUO Wangmeng, CHEN Yunjin, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142–3155. doi: 10.1109/TIP.2017.2662206 KIM Y, HWANG I, and CHO N I. A new convolutional network-in-network structure and its applications in skin detection, semantic segmentation, and artifact reduction[J/OL]. arXiv preprint arXiv: 1701.06190. http://arxiv.org/abs/1701.06190, 2017. SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going deeper with convolutions[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 1–9. LIU Pengju, ZHANG Hongzhi, ZHANG Kai, et al. Multi-level Wavelet-CNN for image restoration[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, USA, 2018: 886–895. RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. The 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 2015: 234–241. GUO Jun and CHAO Hongyang. One-to-many network for visually pleasing compression artifacts reduction[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 4867–4876. GALTERI L, SEIDENARI L, BERTINI M, et al. Deep generative adversarial compression artifact removal[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 4836–4845. HUANG Gao, LIU Zhuang, WEINBERGER K Q, et al. Densely connected convolutional networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017, 1: 2261–2269. ZHANG Kai, ZUO Wangmeng, GU Shuhang, et al. Learning deep CNN denoiser prior for image restoration[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017, 2: 2808–2817. KRIZHEVSKY A, SUTSKEVER I, and HINTON G E. ImageNet classification with deep convolutional neural networks[C]. The 25th International Conference on Neural Information Processing Systems, Lake Tahoe, USA, 2012: 1097–1105. -





 下载:
下载:





 下载:
下载:
