A Doppler Resampling Based Imaging Algorithm for High Squint SAR with Constant Acceleration
-
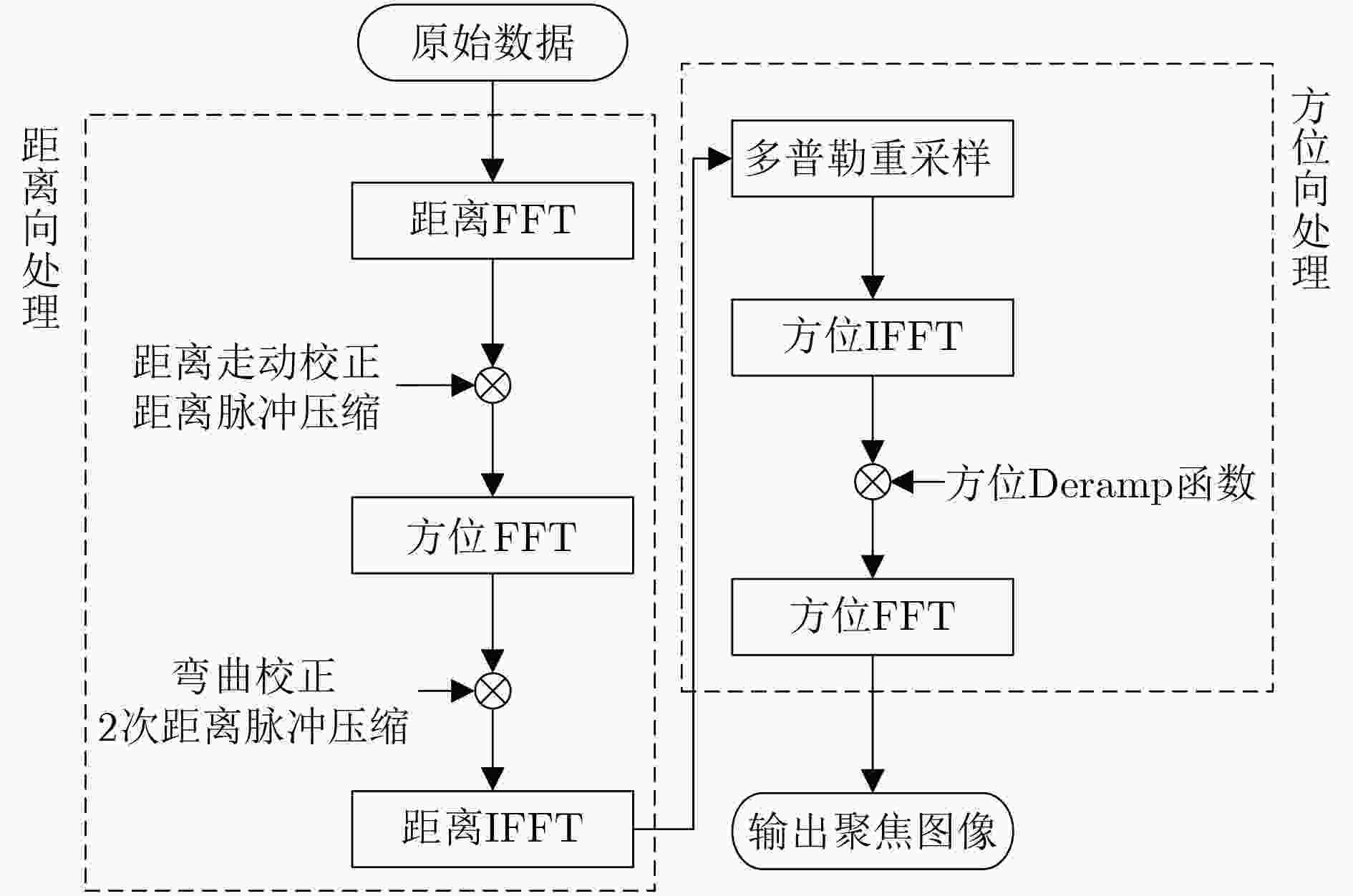
摘要: 针对机动平台大斜视(HS) SAR存在的方位相位系数空变特性,该文提出一种基于多普勒重采样的改进谱分析(SPECAN)成像方法。首先,对于恒加速度HS SAR,给出了一种正交坐标斜距模型,可以处理传统方法中距离走动校正(RWC)引起的坐标旋转,解决了斜距模型与信号之间的失配问题。在此基础上通过方位多普勒重采样校正相位系数的空变性,并且结合SPECAN技术实现方位向聚焦。最后,通过仿真数据验证了该文算法的有效性,与参考算法相比该文方法聚焦质量有明显提升。Abstract: A modified SPECtral ANalysis (SPECAN) algorithm based on Doppler resampling is proposed to deal with the azimuth Space-Variant (SV) phase coefficients of the High Squint (HS) SAR data acquired from maneuvering platform. Firstly, for HS SAR with constant acceleration, an orthogonal coordinate slant range model is presented, which can handle the coordinate rotation caused by the traditional method of Range Walk Correction (RWC), and solve the mismatch between the range model and the signal after RWC. Then azimuth Doppler resampling is used to correct the SV phase coefficients. The focused image is achieved by SPECAN technique. Finally, the proposed algorithm is validated by processing of simulated SAR data, and has significant improvement on focusing quality over the reference one.
-
表 1 仿真参数
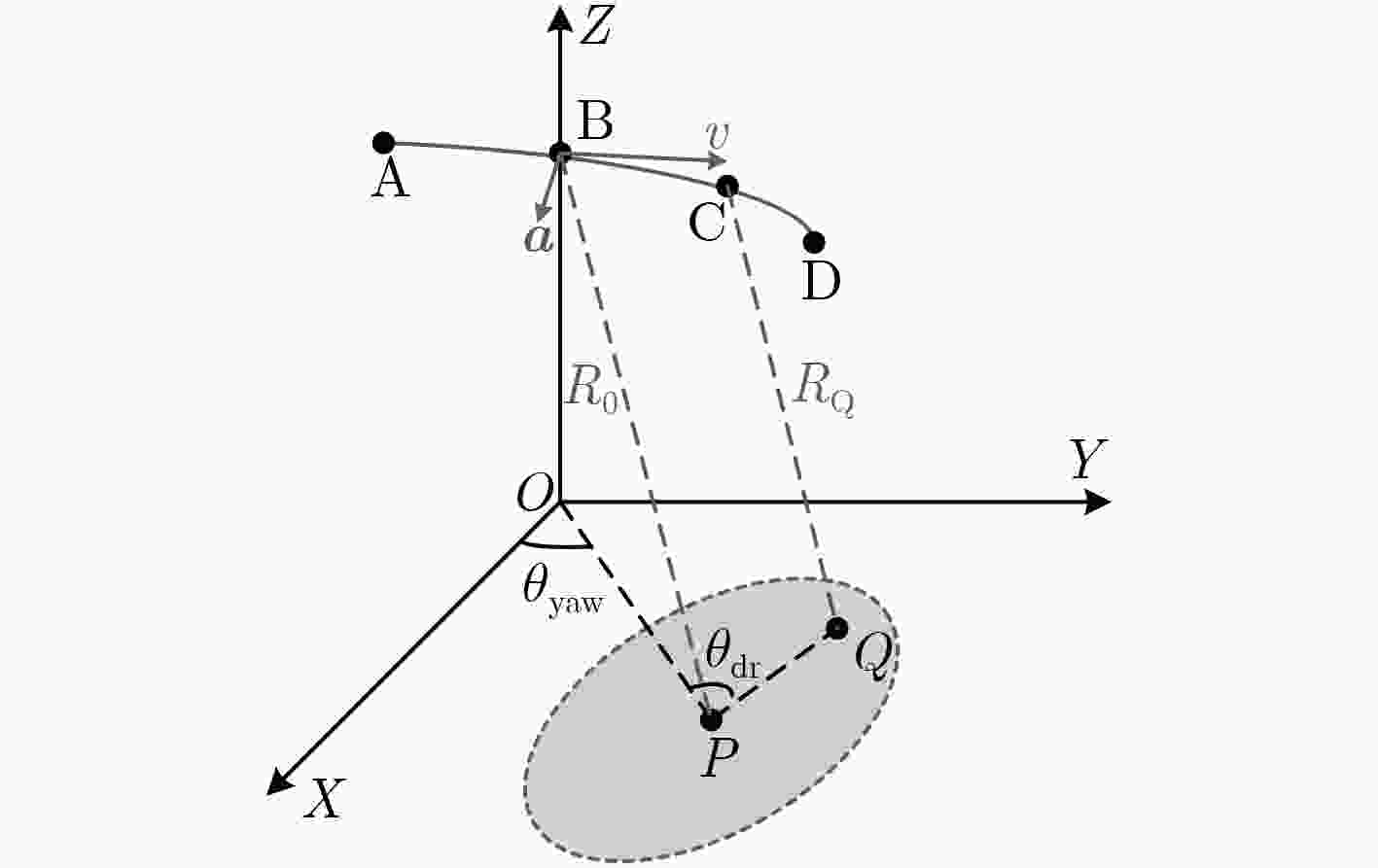
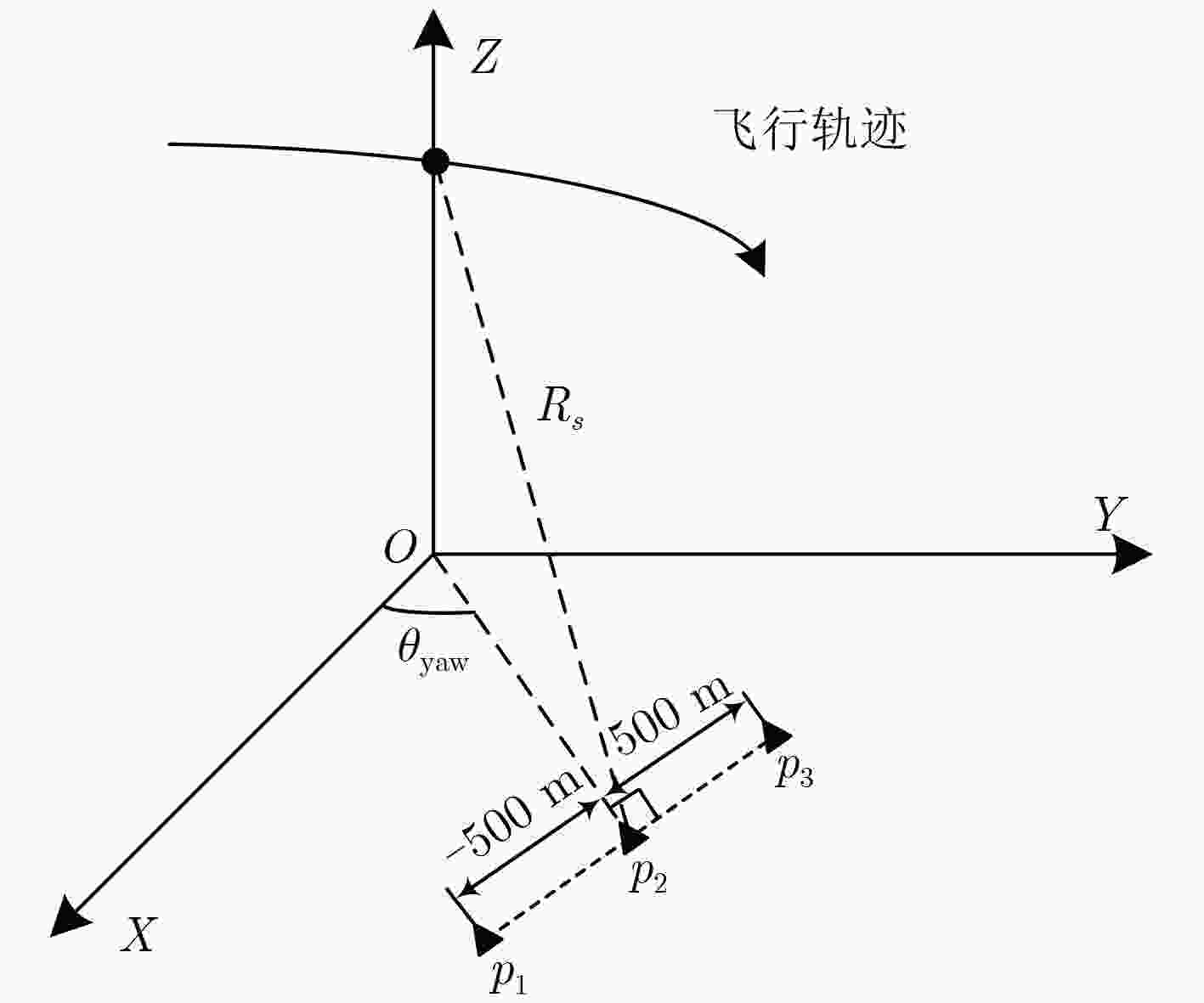
中心频率fc PRF 带宽Br 采样率fs 合成孔径时间Ta 16 GHz 8 kHz 80 MHz 120 MHz 0.3 s 雷达高度H 偏航角 雷达速度矢量${\text{v}}$ 雷达加速度矢量${\text{a}}$ 作用距离Rs 10 km 46° (100, 880, –300) m/s (15, –10, –5) m/s2 18 km 表 2 性能评估指标(dB)
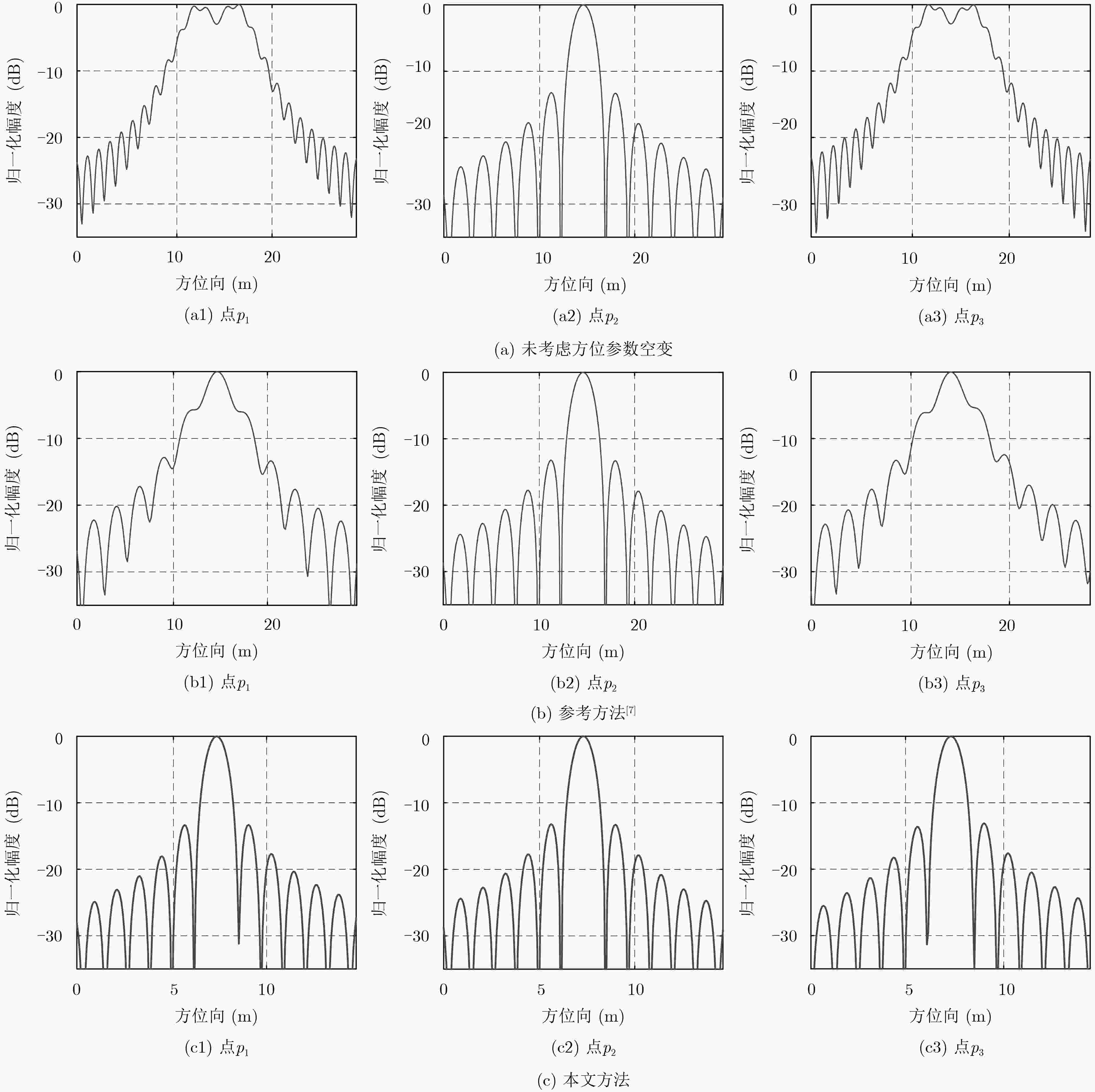
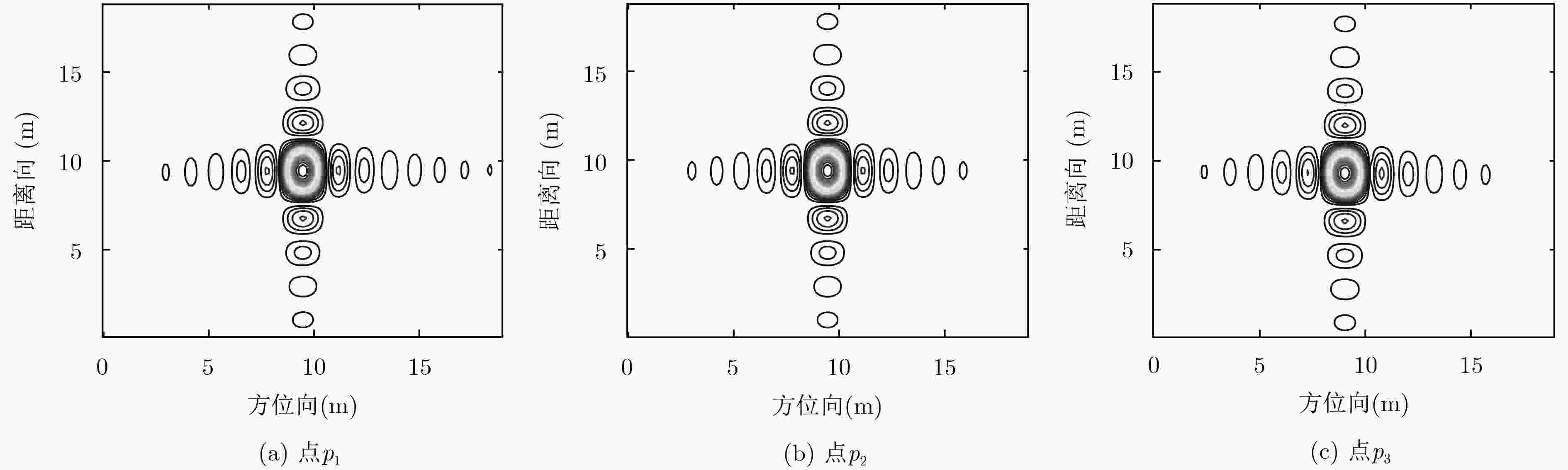
性能指标 点${p_1}$ 点${p_2}$ 点${p_3}$ 参考方法 本文方法 参考方法 本文方法 参考方法 本文方法 峰值旁瓣比 –6.08 –13.32 –12.84 –13.21 –6.33 –13.09 积分旁瓣比 –7.74 –10.02 –11.38 –10.19 –7.82 –10.38 -
保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 1–18.BAO Zheng, XING Mengdao, and WANG Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics industry, 2005: 1–18. CUMMING I G and WONG F H. Digital Processing of Synthetic Aperture Radar Data[M]. Boston, MA: Artech House, 2005: 1–30. LI Zhenyu, XING Mengdao, LIANG Yi, et al. A frequency-domain imaging algorithm for highly squinted SAR mounted on maneuvering platforms with nonlinear trajectory[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 4023–4038. doi: 10.1109/TGRS.2016.2535391 别博文, 孙路, 邢孟道, 等. 基于局部直角坐标和子区域处理的弹载SAR频域成像算法[J]. 电子与信息学报, 2018, 40(8): 1779–1786. doi: 10.11999/JEIT171107BIE Bowen, SUN Lu, XING Mengdao, et al. A frequency-domain algorithm based on local Cartesian coordinate and Subregion processing for missile-borne SAR imaging[J]. Journal of Electronics &Information Technology, 2018, 40(8): 1779–1786. doi: 10.11999/JEIT171107 郭语, 李一楠, 武晓鹏. 一种深空探测雷达信号处理精度校准方法[J]. 空间电子技术, 2018, 15(3): 65–69. doi: 10.3969/j.issn.1674-7135.2018.03.014GUO Yu, LI Yinan, and WU Xiaopeng. A calibrating method of radar signal processing precision for deep space exploration[J]. Space Electronic Technology, 2018, 15(3): 65–69. doi: 10.3969/j.issn.1674-7135.2018.03.014 LIANG Yi, LI Zhenyu, ZENG Letian, et al. A high-order phase correction approach for focusing HS-SAR small-aperture data of high-speed moving platforms[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(9): 4551–4561. doi: 10.1109/JSTARS.2015.2459765 别博文, 梁毅, 党彦锋, 等. 曲线轨迹SAR大斜视子孔径成像算法[J]. 系统工程与电子技术, 2017, 39(3): 500–505. doi: 10.3969/j.issn.1001-506X.2017.03.07BIE Bowen, LIANG Yi, DANG Yanfeng, et al. Sub-aperture imaging algorithm for high squint SAR with curvilinear flight tracks[J]. Systems Engineering and Electronics, 2017, 39(3): 500–505. doi: 10.3969/j.issn.1001-506X.2017.03.07 李震宇, 梁毅, 邢孟道, 等. 弹载合成孔径雷达大斜视子孔径频域相位滤波成像算法[J]. 电子与信息学报, 2015, 37(4): 953–960. doi: 10.11999/JEIT140618LI Zhenyu, LIANG Yi, XING Mengdao, et al. A frequency phase filtering imaging algorithm for highly squint missile-borne synthetic aperture radar with subaperture[J]. Journal of Electronics &Information Technology, 2015, 37(4): 953–960. doi: 10.11999/JEIT140618 SUN Guangcai, XING Mengdao, WANG Tong, et al. A 2-D space-variant chirp scaling algorithm based on the RCM equalization and subband synthesis to process geosynchronous SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4868–4880. doi: 10.1109/TGRS.2013.2285721 游冬, 孙光才, 李亚超, 等. 地球同步轨道SAR两维奇异值分解成像方法[J]. 系统工程与电子技术, 2018, 40(10): 2200–2206. doi: 10.3969/j.issn.1001-506X.2018.10.07YOU Dong, SUN Guangcai, LI Yachao, et al. Two-dimension SVD imaging method for GEO SAR[J]. Systems Engineering and Electronics, 2018, 40(10): 2200–2206. doi: 10.3969/j.issn.1001-506X.2018.10.07 LIU Wenkang, SUN Guangcai, XIA Xianggen, et al. A modified CSA based on joint time-Doppler resampling for MEO SAR stripmap mode[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(6): 3573–3586. doi: 10.1109/TGRS.2018.2802545 YANG Lei, XING Mengdao, WANG Yong, et al. Compensation for the NsRCM and phase error after polar format resampling for airborne spotlight SAR raw data of high resolution[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 165–169. doi: 10.1109/LGRS.2012.2196676 XING Mengdao, WU Yufeng, ZHANG Y D, et al. Azimuth resampling processing for highly squinted synthetic aperture radar imaging with several modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4339–4352. doi: 10.1109/TGRS.2013.2281454 ZENG Tao, LI Yinghe, DING Zegang, et al. Subaperture approach based on azimuth-dependent range cell migration correction and azimuth focusing parameter equalization for maneuvering high-squint-mode SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(12): 6718–6734. doi: 10.1109/TGRS.2015.2447393 -





 下载:
下载:


 下载:
下载:
