Nonlinear Distortion Suppression in Cooperative Jamming Cancellation System
-
摘要: 在同时同频扰中通(CJ)系统中，干扰发射机中的功率放大器(PA)工作于非线性区内，导致近端接收机接收到的自干扰(SI)信号中包含大量非线性分量。该文针对非线性干扰抑制这一问题，在接收端建立干扰非线性模型，并进行非线性模型参数估计，最终在接收信号中减去重建的非线性干扰信号，以抑制同时同频扰中通系统中的非线性干扰。仿真与实验结果表明，该文所提方法针对同时同频扰中通场景中存在残余频偏的情况下，能够对非线性干扰进行有效抑制，验证了该方案的有效性与可行性。Abstract: In Cooperative Jamming (CJ) system, the Power Amplifier (PA) in the jamming transmitter works in nonlinear region, which results in a large number of nonlinear components in the Self-Interference (SI) signal received by the near-end receiver. To solve the problem of nonlinear distortion suppression, a nonlinear model is established at the receiver. Then, the reconstructed nonlinear signal based on the estimated parameters is subtracted from the received signal to suppress the nonlinear interference in CJ. Simulation and experimental results indicate that the nonlinear suppression scheme proposed in this paper can further suppress the nonlinear interference under the residual frequency offset in CJ, and verify the effectiveness and feasibility of the proposed scheme.
-
HONG S, BRAND J, CHOI J I, et al. Applications of self-interference cancellation in 5G and beyond[J]. IEEE Communications Magazine, 2014, 52(2): 114–121. doi: 10.1109/MCOM.2014.6736751 王俊, 赵宏志, 卿朝进, 等. 同时同频全双工场景中的射频域自适应干扰抵消[J]. 电子与信息学报, 2014, 36(6): 1435–1440. doi: 10.3724/SP.J.1146.2013.01187WANG Jun, ZHAO Hongzhi, QING Chaojin, et al. Adaptive self-interference cancellation at RF domain in co-frequency co-time full duplex systems[J]. Journal of Electronics &Information Technology, 2014, 36(6): 1435–1440. doi: 10.3724/SP.J.1146.2013.01187 LIU Ying, ROBLIN P, QUAN Xin, et al. A full-duplex transceiver with two-stage analog cancellations for multipath self-interference[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(12): 5263–5273. doi: 10.1109/TMTT.2017.2752167 LI Chenxing, ZHAO Hongzhi, WU Fei, et al. Digital self-interference cancellation with variable fractional delay FIR filter for full-duplex radios[J]. IEEE Communications Letters, 2018, 22(5): 1082–1085. doi: 10.1109/LCOMM.2018.2810270 ZHANG Guangchi, XU Jie, WU Qingqing, et al. Wireless powered cooperative jamming for secure OFDM system[J]. IEEE Transactions on Vehicular Technology, 2018, 67(2): 1331–1346. doi: 10.1109/TVT.2017.2756877 MA Hui, CHENG Julian, WANG Xianfu, et al. Robust MISO beamforming with cooperative jamming for secure transmission from perspectives of QoS and secrecy rate[J]. IEEE Transactions on Communications, 2018, 66(2): 767–780. doi: 10.1109/TCOMM.2017.2765637 PARK K H, WANG Tian, and ALOUINI M S. On the jamming power allocation for secure amplify-and-forward relaying via cooperative jamming[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(9): 1741–1750. doi: 10.1109/JSAC.2013.130908 ZHENG Gan, CHOO L C, and WONG K K. Optimal cooperative jamming to enhance physical layer security using relays[J]. IEEE Transactions on Signal Processing, 2011, 59(3): 1317–1322. doi: 10.1109/TSP.2010.2092774 SCOTT K E and OLASZ E B. Simultaneous clock phase and frequency offset estimation[J]. IEEE Transactions on Communications, 1995, 43(7): 2263–2270. doi: 10.1109/26.392969 QUAN Xin, LIU Ying, PAN Wensheng, et al. A two-stage analog cancellation architecture for self-interference suppression in full-duplex communications[C]. 2017 IEEE MTT-S International Microwave Symposium, Honololu, USA, 2017: 1169–1172. doi: 10.1109/MWSYM.2017.8058808. AHMED E and ELTAWIL A M. All-digital self-interference cancellation technique for full-duplex systems[J]. IEEE Transactions on Wireless Communications, 2015, 14(7): 3519–3532. doi: 10.1109/TWC.2015.2407876 BHARADIA D, MCMILIN E, and KATTI S. Full duplex radios[J]. ACM SIGCOMM Computer Communication Review, 2013, 43(4): 375–386. doi: 10.1145/2534169.2486033 SIMON H. Adaptive Filter Theory[M]. 5th ed. Upper Saddle River, New Jersey, Pearson Education, Inc, 2014: 245–253. -
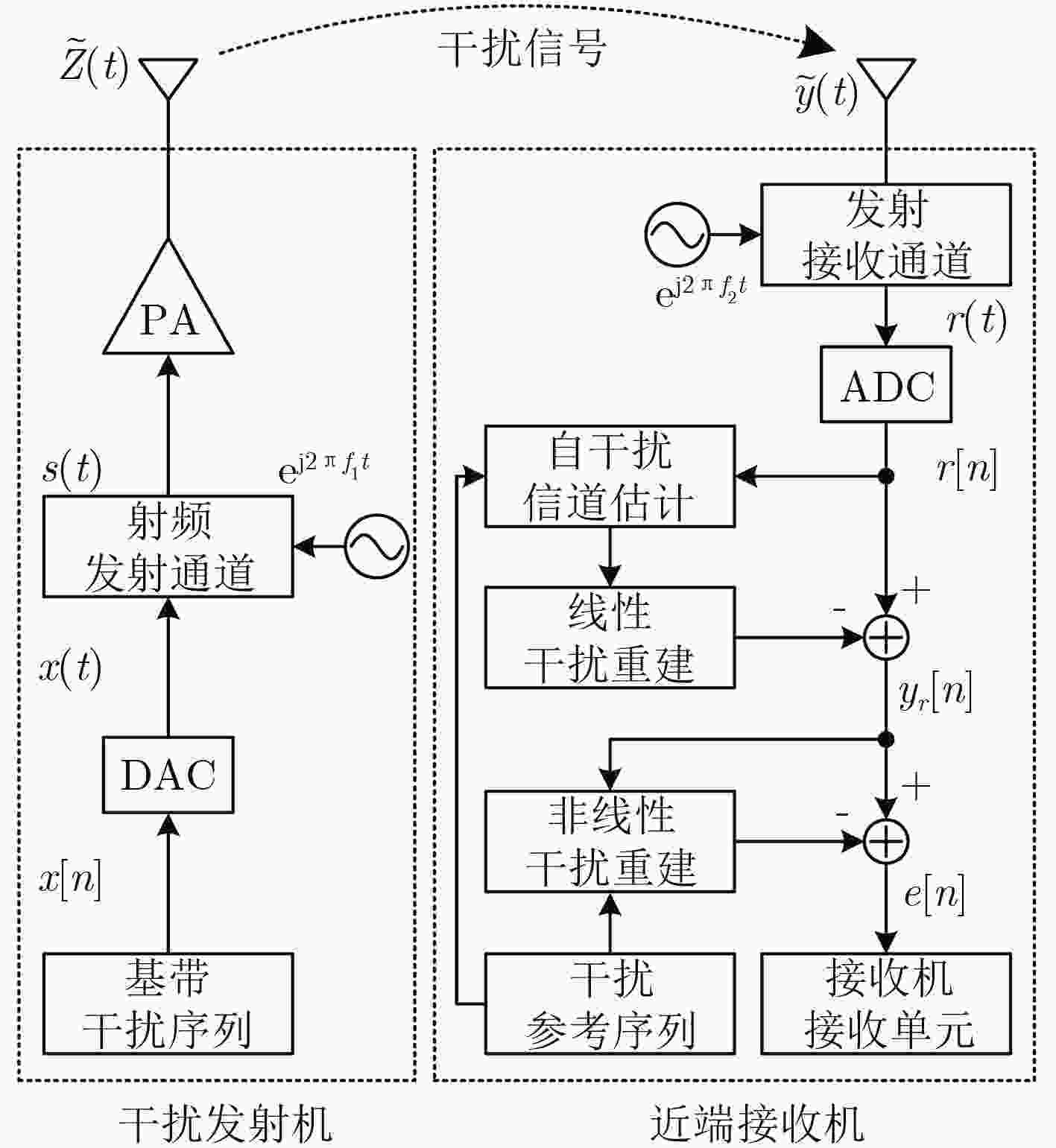
下载:
图(5)
计量
- 文章访问数: 2565
- HTML全文浏览量: 989
- PDF下载量: 128
- 被引次数: 0
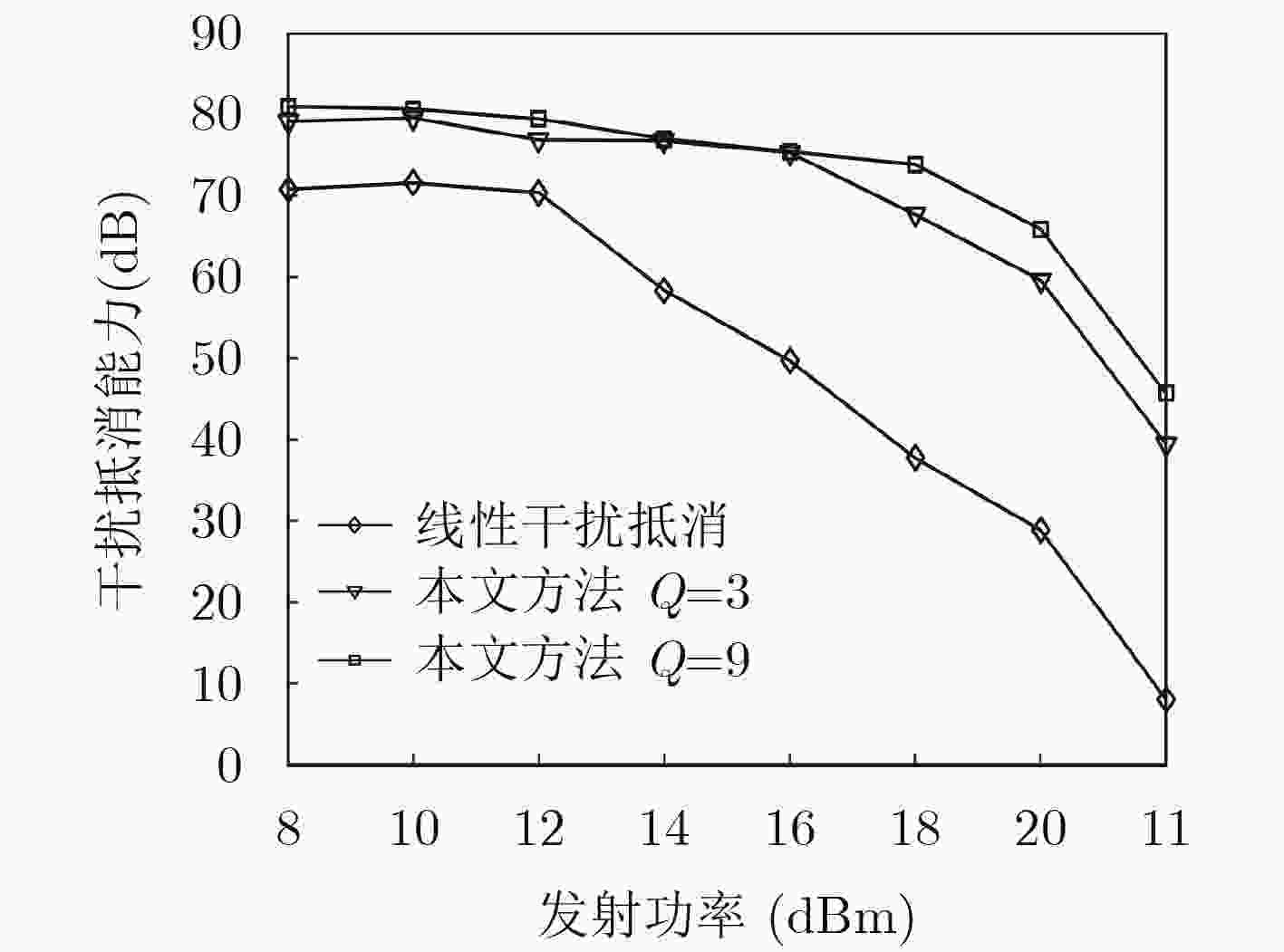
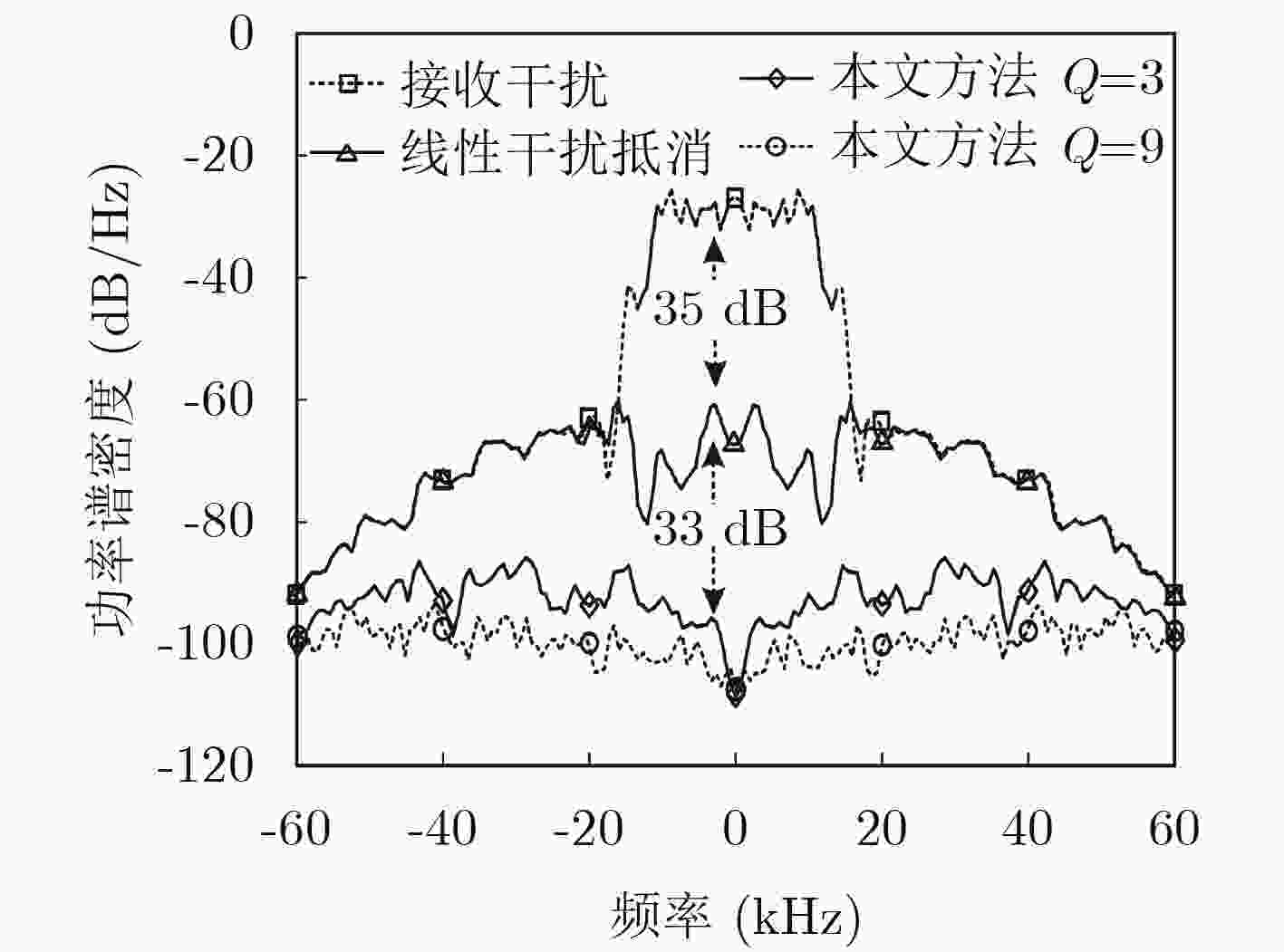
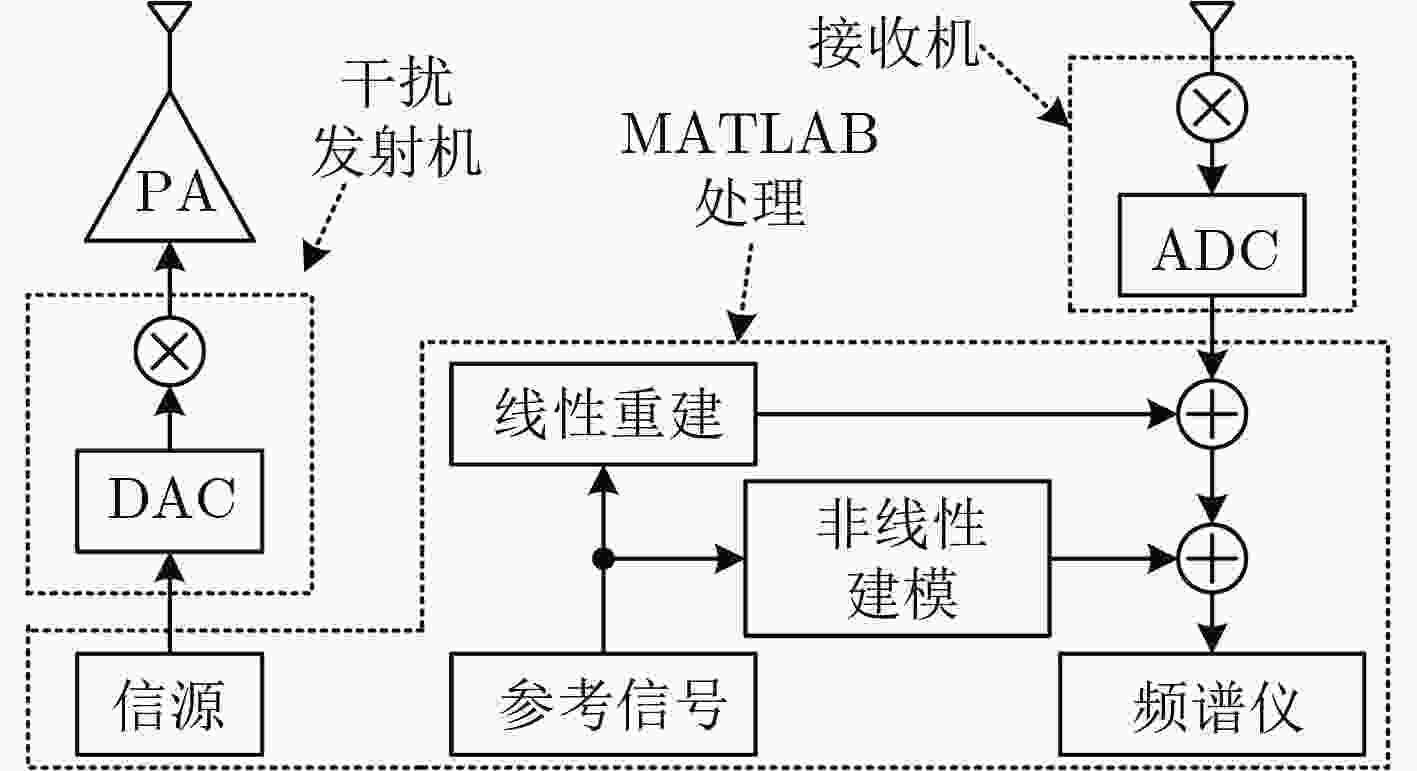
下载:
