减轮Simeck算法的积分攻击

任炯炯; 李航; 陈少真

doi:10.11999/JEIT180849

减轮Simeck算法的积分攻击

doi: 10.11999/JEIT180849

1.
战略支援部队信息工程大学郑州 450001
2.
数学工程与先进计算国家重点实验室郑州 450001

基金项目: 国家密码发展基金(MMJJ20180203)；数学工程与先进计算国家重点实验室开放基金(2018A03)；信息保障技术重点实验室开放基金(KJ-17-002)

详细信息

作者简介:
任炯炯：男，1994年生，博士生，研究方向为对称密码设计与分析

李航：男，1995年生，硕士生，研究方向为对称密码设计与分析

陈少真：女，1967年生，教授，研究方向为密码学与信息安全

通讯作者:
任炯炯　jiongjiong_fun@163.com

中图分类号: TN918.1
计量
- 文章访问数: 2754
- HTML全文浏览量: 1135
- PDF下载量: 82
- 被引次数: 0
出版历程
- 收稿日期: 2018-08-31
- 修回日期: 2019-03-14
- 网络出版日期: 2019-04-01
- 刊出日期: 2019-09-10

Integral Attack on Reduced-round Simeck Algorithm

1.
PLA Information Engineering University, Zhengzhou 450001, China
2.
State Key Laboratory of Mathematical Engineering and Advanced Computing, Zhengzhou 450001, China

Funds: The National Cipher Development Foundation (MMJJ20180203); The State Key Laboratory of Mathematical Engineering and Advanced Computation Open Foundation (2018A03); The Foundation of Science and Technology on Information Assurance Laboratory (KJ-17-002)

摘要

摘要: 该文对轻量级分组密码算法Simeck在积分攻击下的安全性进行了研究。通过向前解密扩展已有的积分区分器，构造了16轮Simeck48和20轮Simeck64算法的高阶积分区分器，并在新区分器的基础上，利用等价子密钥技术和部分和技术，结合中间相遇策略和密钥扩展算法的性质，实现了24轮Simeck48和29轮Simeck64算法的积分攻击。攻击24轮Simeck48的数据复杂度为2⁴⁶，时间复杂度为2⁹⁵，存储复杂度为2^82.52；攻击29轮Simeck64的数据复杂度为2⁶³，时间复杂度为2^127.3，存储复杂度为2^109.02。与Simeck算法已有积分攻击的结果相比，该文对Simeck48和Simeck64积分攻击的轮数分别提高了3轮和5轮。
- 密码分析 /
- 轻量级分组密码 /
- 积分攻击 /
- Simeck算法
Abstract: The security of lightweight block cipher Simeck against integral attack is evaluated in this paper. First, a 16-round and a 20-round high-order integral distinguisher of Simeck48 and Simeck64 are constructed by decrypting the existed integral distinguisher forward. Then, combined with the meet-in-the-middle strategy and subkey relationship, the integral attacks on 24-round Simeck48 and 29-round Simeck64 are first proposed utilizing the equivalent-subkey and partial-sum technologies based on the new integral distinguishers. The data, time and memory complexity of attacking 24-round Simeck48 are 2⁴⁶, 2⁹⁵ and 2^82.52 while the data, time and memory complexity of attacking 29-round Simeck64 are 2⁶³, 2^127.3 and 2^109.02. These new attacks improve greatly the results of the previous integral attack on Simeck. Compared with the known results of the integral attack on Simeck, the number of rounds of the integral attacks on Simeck48 and Simeck64 is increased by 3-round and 5-round, respectively.
- Cryptanalysis /
- Lightweight block cipher /
- Integral attack /
- Simeck algorithm

HTML全文

图 1 Simeck算法的轮函数

下载: 全尺寸图片幻灯片

图 2 等价子密钥技术

下载: 全尺寸图片幻灯片

图 3 中间相遇策略

下载: 全尺寸图片幻灯片

图 4 Tb₁的计算

下载: 全尺寸图片幻灯片

表 1 符号说明

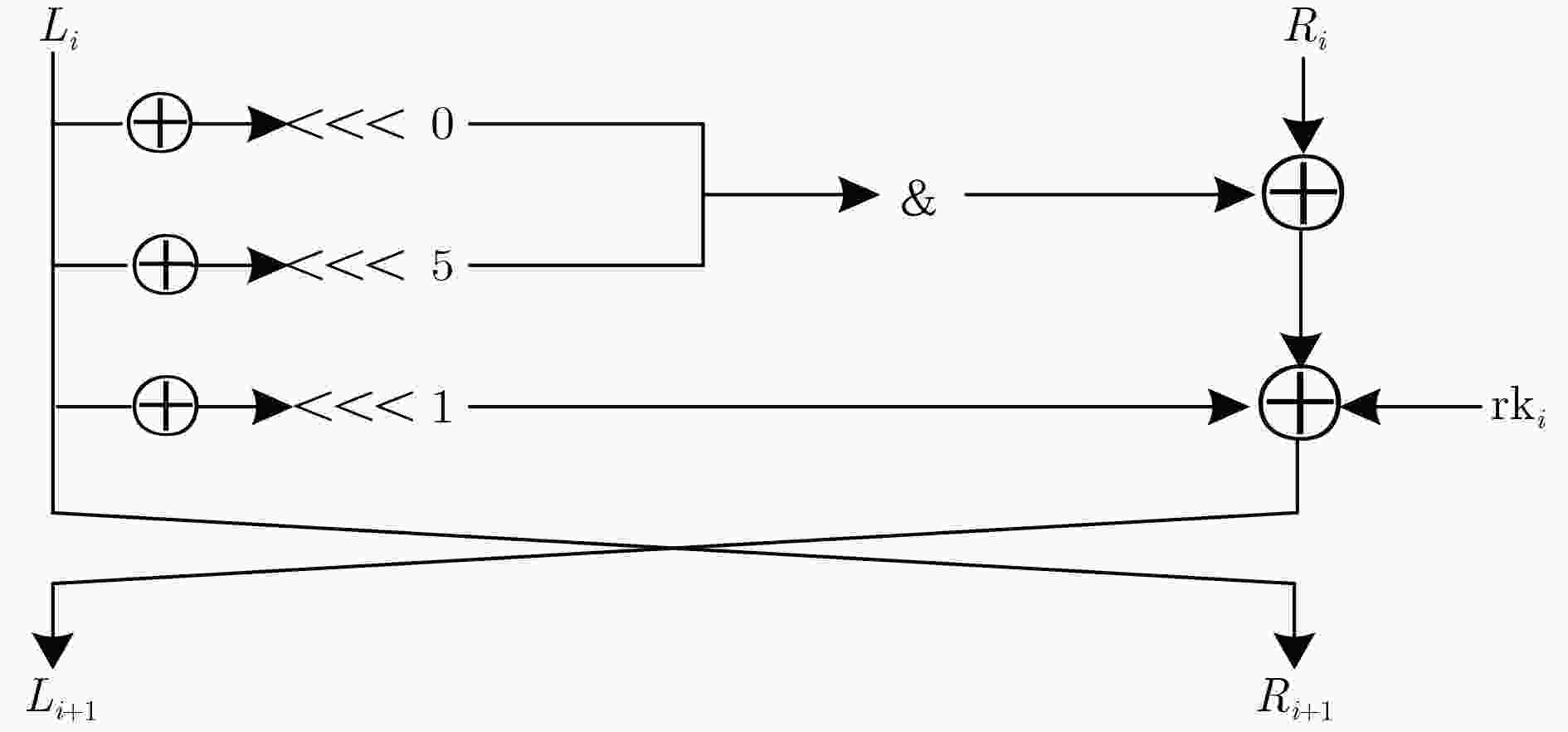
符号	说明
Simeck2n(4n)	分组为2n，密钥为4n的Simeck算法
${{L} _i}$	第i轮左半部分输入nbit
${L_i}\left( j \right)$	${{L} _i}$第j bit
${{R} _i}$	第i轮右半部分输入nbit
${R_i}\left( j \right)$	${{R} _i}$第j bit
${K} $	主密钥${K} = ({{K} _3},{{K} _2},{{K} _1},{{K} _0})$
${\rm{r}}{{\rm{k}}_i}$	第i轮nbit的轮子密钥
$ \oplus $	异或运算
$\& $,$ \odot $	与运算
$ < < < r$, $ > > > r$	循环左移、右移rbit

下载: 导出CSV

表 2 Simeck算法的参数

算法	分组长度	密钥长度	字长	轮数
Simeck	32	64	16	32
	48	96	24	36
	64	128	32	44

下载: 导出CSV

表 3 Simeck48的主要攻击结果

算法	攻击方法	攻击轮数	数据复杂度	存储复杂度	时间复杂度	成功概率	参考文献
Simeck48(96)	差分攻击	20	${O} ({2^{46}})$	–	2⁷⁵	1	文献[2]
Simeck48(96)	差分攻击	26	${O} ({2^{47}})$	–	2⁶²	1	文献[4]
Simeck48(96)	差分攻击	28	${O} ({2^{46}})$	–	2^68.3	0.468	文献[5]
Simeck48(96)	线性攻击	19	${O} ({2^{45}})$	–	2⁹⁴	1	文献[3]
Simeck48(96)	不可能差分	24	${O} ({2^{48}})$	${O} ({2^{74}})$	2^94.7	1	文献[2]
Simeck48(96)	零相关攻击	24	${O} ({2^{48}})$	${O} ({2^{65.06}})$	2^91.6	1	文献[6]
Simeck48(96)	积分攻击	21	${O} ({2^{34}})$	${O} ({2^{66}})$	2⁹⁵	1	文献[7]
Simeck48(96)	积分攻击	24	${O} ({2^{46}})$	${O} ({2^{82.52}})$	2⁹⁵	1	本文

下载: 导出CSV

表 4 Simeck64的主要攻击结果

算法	攻击方法	攻击轮数	数据复杂度	存储复杂度	时间复杂度	成功概率	参考文献
Simeck64(128)	差分攻击	26	${O} ({2^{63}})$	–	2¹²¹	1	文献[2]
Simeck64(128)	差分攻击	33	${O} ({2^{63}})$	${O} ({2^{63}})$	2⁹⁶	1	文献[4]
Simeck64(128)	差分攻击	35	${O} ({2^{63}})$	–	2^116.3	0.555	文献[5]
Simeck64(128)	线性攻击	27	${O} ({2^{61}})$	–	2^120.5	0.477	文献[3]
Simeck64(128)	不可能差分	25	${O} ({2^{64}})$	${O} ({2^{79}})$	2^126.6	1	文献[2]
Simeck64(128)	零相关攻击	28	${O} ({2^{64}})$	${O} ({2^{97.67}})$	2^123.06	1	文献[6]
Simeck64(128)	积分攻击	24	${O} ({2^{35}})$	${O} ({2^{90.46}})$	2¹²⁷	1	文献[7]
Simeck64(128)	积分攻击	29	${O} ({2^{63}})$	${O} ({2^{109.02}})$	${2^{127.3}}$	1	本文

下载: 导出CSV

参考文献(16)

BEAULIEU R, SHORS D, SMITH J, et al. The SIMON and SPECK families of lightweight block ciphers[EB/OL]. http://eprint.iacr.org/2013/404, 2013.

YANG Gangqiang, ZHU Bo, SUDER V, et al. The Simeck family of lightweight block ciphers[C]. Proceedings of the 17th International Workshop on Cryptographic Hardware and Embedded Systems 2015, Saint-Malo, France, 2015: 307–329.

BAGHERI N. Linear cryptanalysis of reduced-round Simeck variants[C]. The 16th International Conference on Cryptology in India, Bangalore, India, 2015: 140–152.

KÖLBL S and ROY A. A brief comparison of Simon and Simeck[C]. The 5th International Workshop on Lightweight Cryptography for Security and Privacy, Aksaray, Turkey, 2016: 69–88.

BLONDEAU C, BOGDANOV A and WANG M. On the (In)equivalence of impossible differential and zero-correlation distinguishers for Feistel- and Skipjack-type ciphers[C]. The 12-th International Conference on Applied Cryptography and Network Security, Lausanne, Switzerland, 2014: 271–288.

ZHANG Kai, GUAN Jie, HU Bin, et al. Security evaluation on Simeck against zero-correlation linear cryptanalysis[J]. IET Information Security, 2018, 12(1): 87–93. doi: 10.1049/iet-ifs.2016.0503

ZHANG Kai, GUAN Jie, HU Bin, et al. Integral cryptanalysis on Simeck[C]. The Sixth International Conference on Information Science and Technology, Dalian, China, 2016: 216–222.

DAEMEN J, KNUDSEN L R, and RIJMEN V. The block cipher square[C]. The 4th International Workshop on Fast Software Encryption, Haifa, Israel, 1997: 149–165.

LUCKS S. The saturation attack—A bait for Twofish[C]. The 8th International Workshop on Fast Software Encryption, Yokohama, Japan, 2001: 1–15.

BIRYUKOV A and SHAMIR A. Structural cryptanalysis of SASAS[C]. International Conference on the Theory and Application of Cryptographic Techniques: Advances in Cryptology, Innsbruck, Austria, 2001: 395–405.

KNUDSEN L and WAGNER D. Integral cryptanalysis[C]. The 9th International Workshop on Fast Software Encryption, Leuven, Belgium, 2002: 112–127.

ZHANG Wentao, SU Bozhan, WU Wenling, et al. Extending higher-order integral: An efficient unified algorithm of constructing integral distinguishers for block ciphers[C]. The 10th International Conference on Applied Cryptography and Network Security, Singapore, 2012: 117–134.

ISOBE T and SHIBUTANI K. Generic key recovery attack on Feistel scheme[C]. The 19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, 2013: 464–485.

FERGUSON N, KELSEY J, LUCKS S, et al. Improved cryptanalysis of Rijndael[C]. The 7th International Workshop on Fast Software Encryption, New York, USA, 2000: 213–230.

YI Wentan, WU Baofeng, CHEN Shaozhen, et al. Improved integral and zero-correlation linear cryptanalysis of CLEFIA block cipher[C]. The 12th International Conference on Information Security and Cryptology, Beijing, China, 2016: 33–46.

FUNABIKI Y, TODO Y, ISOBE T, et al. Improved integral attack on HIGHT[C]. The 22nd Australasian Conference on Information Security and Privacy, Auckland, New Zealand, 2017: 363–383.

施引文献

资源附件(0)

访问统计