Blind Estimation of the Pseudo Noise Sequence and Information Sequence for Short Code Synchronous and Asynchronous DS-CDMA Signal
-
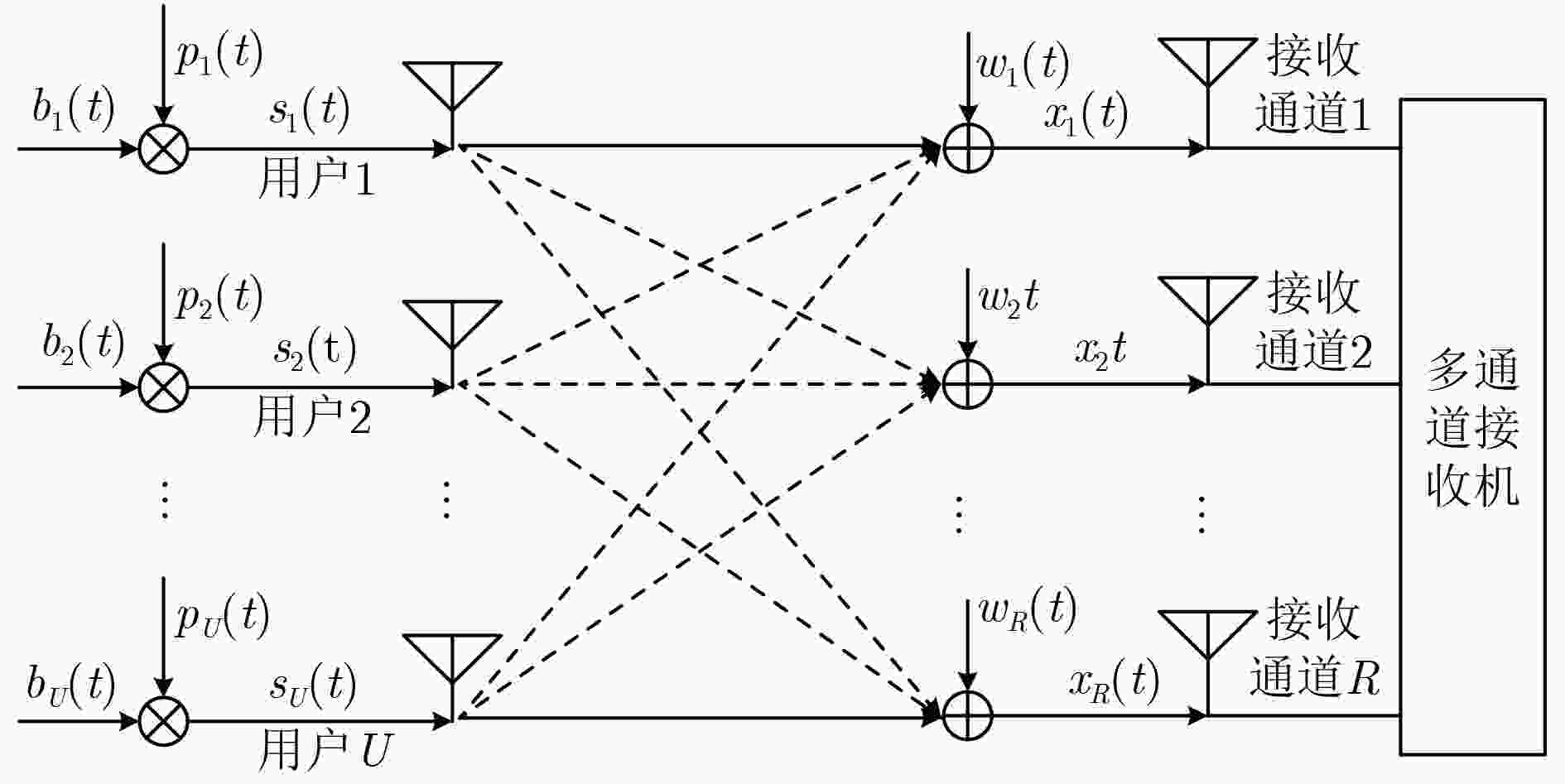
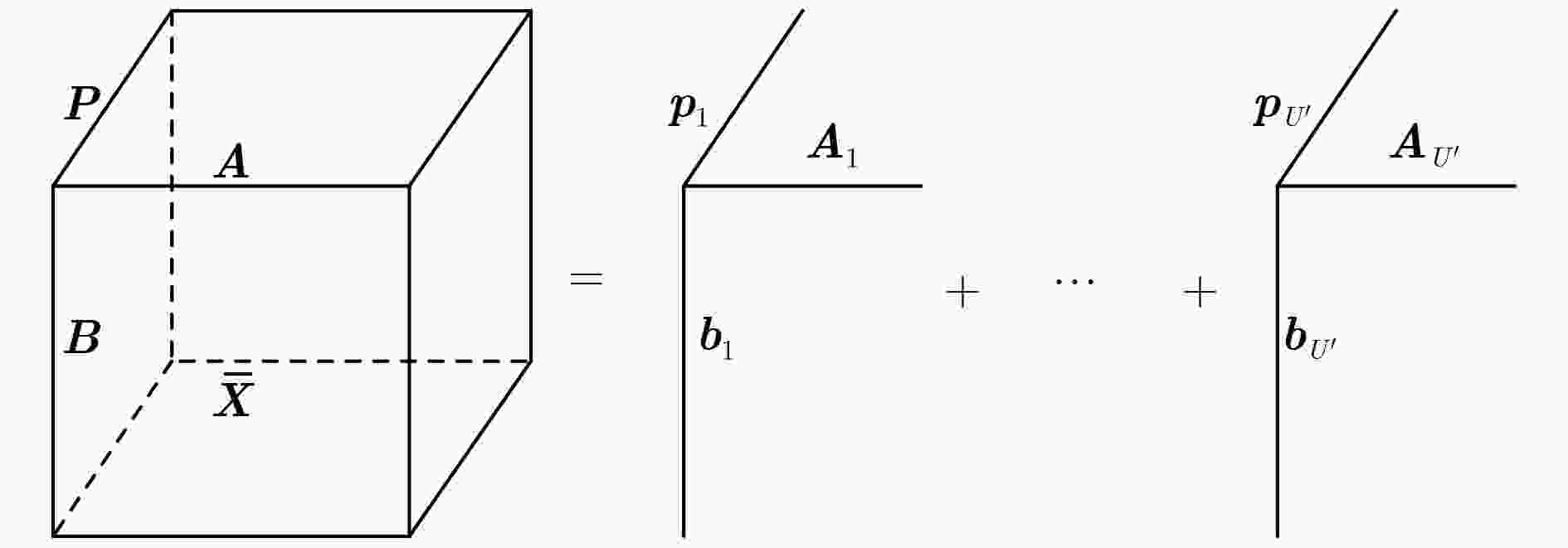
摘要: 针对传统单通道异步直接序列码分多址(DS-CDMA)信号信息序列及伪码序列(PN)难以估计的问题,该文提出一种基于平行因子(PARAFAC)的多通道盲估计方法。该方法首先将信号建模为多通道接收模型,然后将观测数据矩阵等效为平行因子模型,最后使用迭代最小二乘算法对平行因子进行低秩分解,进一步完成对DS-CDMA信号各用户的信息序列及伪码序列进行估计。仿真实验表明,该方法不仅能有效地对同步、异步短码DS-CDMA信号的伪码序列及信息序列进行估计,而且能在通道数为6、信噪比(SNR)为–10 dB的条件下,实现10个用户伪码序列的有效估计。
-
关键词:
- 直接序列码分多址信号 /
- 平行因子 /
- 信息序列 /
- 伪码序列
Abstract: For the problem of Direct Sequence-Code Division Multiple Access (DS-CDMA) signal in traditional asynchronous single-channel, including blind estimation of the Pseudo-Noise (PN) sequence and information sequence, a method using multi-channel synchronous and asynchronous based on PARAllel FACtor (PARAFAC) is proposed. Firstly, the signal is modeled as a multi-channel receiving model, then the observed data matrix is equivalent to a factor model. Finally, the iterative least squares algorithm is applied to decomposing the parallel factor, and the information sequence and PN sequences of DS-CDMA signals are further estimated. The simulation results show that the proposed method can effectively estimate the PN sequence and information sequence of the short code DS-CDMA signal, and the estimation of 6 user PN sequences can be realized under the condition that the number of channels is 10 and the Signal-to-Noise Ratio (SNR) is –10 dB. -
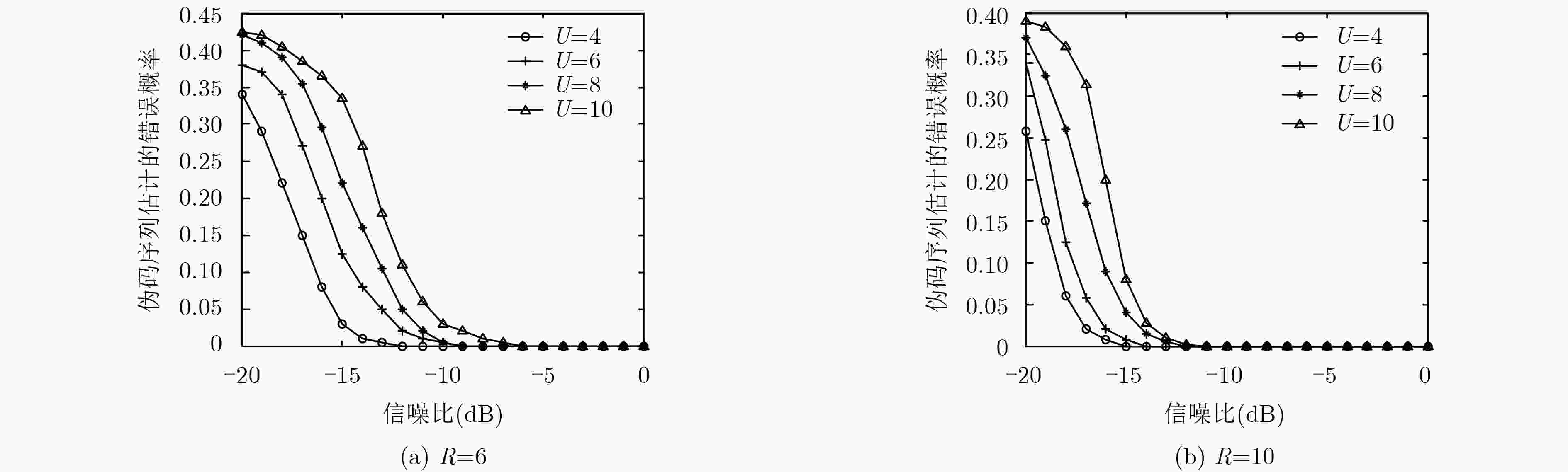
图 7 异步时本文方法与文献[9]方法对比性能曲线
图 8 异步时本文方法与文献[9]方法对比性能曲线
-
田日才, 迟永钢. 扩频通信[M]. 2版. 北京: 清华大学出版社, 2014: 1–5.TIAN Ricai and CHI Yonggang. Spread Spectrum Communication[M]. 2nd ed. Beijing: Tsinghua University Press, 2014: 1–5. LUO Zhongqiang and ZHU Lidong. A charrelation matrix-based blind adaptive detector for DS-CDMA Systems[J]. Sensors, 2015, 15(8): 20152–20168. doi: 10.3390/s150820152 张天骐, 杨强, 宋玉龙, 等. 基于相似度的直扩信号盲解扩方法[J]. 系统工程与电子技术, 2017, 39(7): 1451–1456. doi: 10.3969/j.issn.1001-506X.2017.07.04ZHANG Tianqi, YANG Qiang, SONG Yulong, et al. Similarity based blind despread method of DS-SS signal[J]. Systems Engineering and Electronics, 2017, 39(7): 1451–1456. doi: 10.3969/j.issn.1001-506X.2017.07.04 ZHOU Liqing, LEUNG H, XU Peng, et al. The Kalman filtering blind adaptive multi-user detector based on tracking algorithm of signal subspace[J]. Information, 2015, 6(1): 3–13. doi: 10.3390/info6010003 赵知劲, 李淼, 尚俊娜. 基于矩阵填充和三阶相关的长短码DS-CDMA信号多伪码盲估计[J]. 电子与信息学报, 2016, 38(7): 1788–1793. doi: 10.11999/JEIT151087ZHAO Zhijin, LI Miao, and SHANG Junna. Blind estimation of LSC-DS-CDMA signal based on matrix completion and triple correlation[J]. Journal of Electronics &Information Technology, 2016, 38(7): 1788–1793. doi: 10.11999/JEIT151087 GU Xiaowei, ZHAO Zhijin, and SHEN Lei. Blind estimation of pseudo-random codes in periodic long code direct sequence spread spectrum signals[J]. IET Communications, 2016, 10(11): 1273–1281. doi: 10.1049/iet-com.2015.0374 张天骐, 赵军桃, 江晓磊. 基于多主分量神经网络的同步DS-CDMA伪码盲估计[J]. 系统工程与电子技术, 2016, 38(11): 2638–2647. doi: 10.3969/j.issn.1001-506X.2016.11.27ZHANG Tianqi, ZHAO Juntao, and JIANG Xiaolei. PN code sequence blind estimate of synchronous DS-CDMA based on multi-principal component neural network[J]. Systems Engineering and Electronics, 2016, 38(11): 2638–2647. doi: 10.3969/j.issn.1001-506X.2016.11.27 付卫红, 杨小牛, 刘乃安. 基于盲源分离的CDMA多用户检测与伪码估计[J]. 电子学报, 2008, 36(7): 1319–1323. doi: 10.3321/j.issn:0372-2112.2008.07.013FU Weihong, YANG Xiaoniu, and LIU Naian. The multi-user detection and chip sequence estimation for CDMA system based on the blind source separation[J]. Acta Electronica Sinica, 2008, 36(7): 1319–1323. doi: 10.3321/j.issn:0372-2112.2008.07.013 任啸天, 徐晖, 黄知涛, 等. 基于Fast-ICA同、异步系统短码CDMA信号扩频序列与信息序列盲估计[J]. 电子学报, 2011, 39(12): 2726–2732.REN Xiaotian, XU Hui, HUANG Zhitao, et al. Fast-ICA based blind estimation of spreading and information sequences of short-code CDMA signals in synchronous and asynchronous systems[J]. Acta Electronica Sinica, 2011, 39(12): 2726–2732. DE LATHAUWER L and CASTAING J. Tensor-based techniques for the blind separation of DS-CDMA signals[J]. Signal Processing, 2007, 87(2): 322–336. doi: 10.1016/j.sigpro.2005.12.015 ZHANG Tianqi, QIAN Wenrui, ZHANG Gang, et al. Parameter estimation of MC-CDMA signals based on modified cyclic autocorrelation[J]. Digital Signal Processing, 2016, 54: 46–53. doi: 10.1016/j.dsp.2016.03.007 SIDIROPOULOS N D, GIANNAKIS G B, and BRO R. Blind PARAFAC receivers for DS-CDMA systems[J]. IEEE Transactions on Signal Processing, 2000, 48(3): 810–823. doi: 10.1109/78.824675 HARSHMAN R A, HONG S, and LUNDY M E. Shifted factor analysis-Part I: Models and properties[J]. Journal of Chemometrics, 2003, 17(7): 363–378. doi: 10.1002/cem.808 张天骐, 强幸子, 马宝泽, 等. 基于最小二乘的同步多用户非周期长码直扩信号扩频序列估计[J]. 电波科学学报, 2016, 31(6): 1113–1123. doi: 10.13443/j.cjors.2016030201ZHANG Tianqi, QIANG Xingzi, MA Baoze, et al. Estimation of the spread spectrum sequence for synchronous multi-user aperiodic long-code DSSS signals based on least squares[J]. Chinese Journal of Radio Science, 2016, 31(6): 1113–1123. doi: 10.13443/j.cjors.2016030201 张贤达. 矩阵分析与应用[M]. 2版. 北京: 清华大学出版社, 2013: 604–608.ZHANG Xianda. Matrix Analysis and Applications[M]. 2nd ed. Beijing: Tsinghua University Press, 2013: 604–608. -





 下载:
下载:





 下载:
下载:
