Database Ciphertext Retrieval Scheme Based on f-mOPE
-
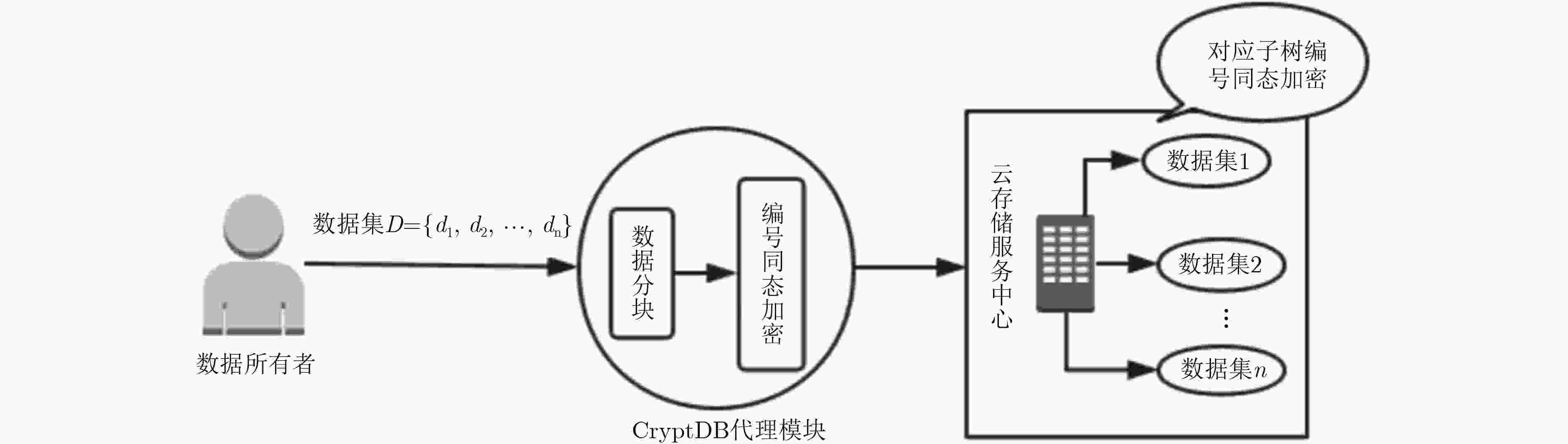
摘要: 在云数据库环境下,为保证云存储数据的安全性,通常将数据加密存储。针对加密存储数据查询开销大,不支持密文排序,查询等缺点,该文提出一种 f-mOPE数据库密文检索方案。该方案基于可变保序编码(mOPE),采用二叉排序树数据结构思想,生成明文一一对应的保序编码;基于AES加密方案将数据明文转化为密文存储;采用改进的部分同态加密算法提升保序加密方案的安全性。通过安全性分析及实验结果表明,该方案在保证数据隐私的基础上,不但能抵御统计型攻击,而且能够有效地降低服务器计算开销,提高数据库处理效率。Abstract: In a cloud database environment, data is usually encrypted and stored to ensure the security of cloud storage data. To overcome the shortcomings of encrypting the data that the query overhead is big, the cipher text sortings and query are not support, etc, this paper puts forward a kind of f - mOPE cryptograph database retrieval scheme. Based on the mOPE sequential encryption algorithm, the idea of binary sort tree data structure is used to generate plaintext one-to-one corresponding sequential coding. Data plaintext is converted into ciphertext storage based on the AES encryption scheme. The improved partial homomorphic encryption algorithm is used to improve the security of sequential encryption scheme. The security analysis and experimental results show that this scheme can not only resist statistical attack, but also reduce effectively server computing cost and improve database processing efficiency on the basis of guaranteeing data privacy.
-
表 1 公式符号说明
$\lambda $:安全参数; $\rho $:噪声长度,为抵抗暴力攻击$\rho = \omega (\lg \lambda )$; $\eta $:私钥二进制长度, $\eta $满足$\eta \ge \rho \varTheta (\lambda {\lg ^2}\lambda )$,这样才能保证压缩 解密可行; $\gamma $:公钥二进制长度,为抵抗格攻击,$\gamma = \omega ({\eta ^2}\lg \lambda )$; $\tau $:公钥个数,$\tau \ge \gamma + \omega (\lg \lambda )$,文中需要的公钥个数为$2\sqrt \tau $; 表 2 序号与保序编码对应关系表
序号 1 2 3 4 5 6 7 8 保序
编码[000]
1=1[00]
10=2[001]
1=3[0]
100=4[010]
1=5[01]
10=6[011]
1=7[1]
000=8[100]
1=9[10]
10=10[1]
011=11[1]
100=12[110]
1=13[11]
10=14[1111]
=15表 3 算法1: 保序编码调整算法
符号定义:ord_num:数据的序号;index:数据十进制编码 //将所有的数据排序后存入临时表tmp中 insertIntoTmpTable(datas) h = lg(n)+1; index = 2(n-(2h-1 -1))+1; count = index-1; //更新临时表中数据索引编码 if(ord_num > count): foreach(): updateTmpTable(ord_num): index = ord_num + (ord_num-count); update tmp set index = index where ord_num=ord_num; else: foreach(): update tmp set index = ord_num where ord_num=ord_num; //将临时表重平衡结果更新至数据表中,需要将临时表中index转换为二进制并加入子树标识,如式(7)描述 foreach(data): update OPE_Table A inner join tmp B on A.ciper = B.ciper set A.ord_code = B.index; 表 4 算法2: 数据插入及检索算法
插入元素算法: 查找元素算法: key,IV = generateInitAttr();//初始化加密参数 //确定子树编码 //加密明文 treeIndex = partitionTree(plainText); ciphertext = encryptData(plainText); //查询子树根节点 //构建保序编码 rootNode = searchTreeRootNode(treeIndex); foreach(plainTexts): //遍历子树寻找所有符合条件密文 //确定子树编码 datalist = search(rootNode,tree,plainText): treeIndex = partitionTree(plainText); foreach(datalist)://解密所有密文 //数据模糊化处理 data = decrypt(value,key); fuzzyData=FuzzyData(plainText); return datalist; //与服务端交互确定数据保序索引 code_index=connectToServer(fuzzyData,treeIndex); //插入数据 insertData(fuzzyData,code_index); 表 5 DGHV部分同态加密方案与本文改进方案对比
DGHV部分同态加密方案 本文改进部分同态加密方案 加密效率 1次加密1 bit明文 1次加密$n$bit明文 安全性 $q$是对外开放的,那么如果 $pq$ 作为公钥,很容易计算出私钥$p$的值。 加入一些明文为0加密得到的密文$\{ {x_i}:{x_i} = {2^n}{r_i} + p{q_i}\} $,将这些密文组成一个集合$s$,以$\sum\nolimits_{1 \le i,j \le \sqrt \tau } {{b_{i,j}}{x_{i,0}}} {x_{j,1}}$作为公钥,任意选取集合元素${x_i} \in S$加入运算,因为其明文都是0,不会改变加密结果,并且能够提高算法安全性。在运算过程中只需要将${2^n}$上传到服务器即可,把${2^n}\sum\nolimits_{1 \le i,j \le \sqrt \tau } {{b_{i,j}}{x_{i,0}}{x_{j,1}}} $作为公钥,即使获取${2^n}$也无法获取密钥$p$ 复杂度 该方案公钥尺寸约为$O({\lambda ^{10}})$ 该方案中,参数取$\rho = \lambda $, $\eta = O({\lambda ^2})$,$\gamma = O({\lambda ^5})$,$\tau = O({\lambda ^3})$,所以该部分同态加密公钥尺寸为$r + \tau (\lambda + \eta ) = O({\lambda ^5})$ 表 6 mOPE与f-mOPE查询开销对比
数据个数 mOPE查询开销 f-mOPE查询开销 500 8 10 5000 11 10 10000 12 10 20000 13 10 50000 15 10 表 7 mOPE与f-mOPE时间复杂度比较
时间复杂度 mOPE f-mOPE 计算OPE编码 $O(\lg n)$ $O(\lg n)$ 调整编码 最好情况O(1)
最坏情况O(n)O(1) 检查是否平衡/需要调整 最好情况O(1)
最坏情况O(n)最好情况O(n)
最坏情况O(n) -
GABEL M and MECHLER J. Secure database outsourcing to the cloud: Side-channels, counter-measures and trusted execution[C]. The 2017 IEEE 30th International Symposium on Computer-Based Medical Systems, Thessaloniki, Greece, 2017: 799–804. 陆海宁. 可隐藏搜索模式的对称可搜索加密方案[J]. 信息网络安全, 2017(1): 38–42. doi: 10.3969/j.issn.1671-1122.2017.01.006LU Haining. Searchable symmetric encryption with hidden search pattern[J]. Netinfo Security, 2017(1): 38–42. doi: 10.3969/j.issn.1671-1122.2017.01.006 DEMERTZIS I and PAPAMANTHOU C. Fast searchable encryption with tunable locality[C]. 2017 ACM International Conference on Management of Data, Chicago, Illinois, USA, 2017: 1053–1067. PENG Tianyue, LIN Yaping, YAO Xin, et al. An efficient ranked multi-keyword search for multiple data owners over encrypted cloud data[J]. IEEE Access, 2018, 6: 21924–21933. doi: 10.1109/ACCESS.2018.2828404 AGRAWAL R, KIERNAN J, SRIKANT R, et al. Order preserving encryption for numeric data[C]. 2004 ACM SIGMOD International Conference on Management of Data, Paris, France, 2004: 563–574. BOLDYREVA A, CHENETTE N, LEE Y, et al. Order-preserving symmetric encryption[C]. The 28th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cologne, Germany, 2009: 224–241. LIU Zheli, CHEN Xiaofeng, YANG Jun, et al. New order preserving encryption model for outsourced databases in cloud environments[J]. Journal of Network and Computer Applications, 2016, 59: 198–207. doi: 10.1016/j.jnca.2014.07.001 TERANISHI I, YUNG M, and MALKIN T. Order-preserving encryption secure beyond one-wayness[C]. The 20th International Conference on the Theory and Application of Cryptology and Information Security, Taiwan, China, 2014: 42–61. MAVROFORAKIS C, CHENETTE N, O’NEILL A, et al. Modular order-preserving encryption, revisited[C]. 2015 ACM SIGMOD International Conference on Management of Data, Melbourne, Australia, 2015: 763–777. ZHANG Huanguo, HAN Wenbao, LAI Xuejia, et al. Survey on cyberspace security[J]. Science China Information Science, 2015, 58(11): 1–43. doi: 10.1007/s11432-015-5433-4 LIU Dongxi and WANG Shenlu. Programmable order-preserving secure index for encrypted database query[C]. The 2012 IEEE 5th International Conference on Cloud Computing, Honolulu, USA, 2012: 502–509. LIU Dongxi and WANG Shenlu. Nonlinear order preserving index for encrypted database query in service cloud environments[J]. Concurrency and Computation: Practice and Experience, 2013, 25(13): 1967–1984. doi: 10.1002/cpe.2992 张成果. CryptDB密文数据库系统研究[D]. [硕士论文], 南京邮电大学, 2017.ZHANG Chengguo. The research of cryptDB encrypted database system[D]. [Master dissertation], Nanjing University of Posts and Telecommunications, 2017. POPA R A, REDFIELD C M S, ZELDOVICH N, et al. processing queries on an encrypted database[J]. Communications of the ACM, 2012, 55(9): 103–111. doi: 10.1145/2330667.2330691 POPA R A, LI F H, and ZELDOVICH N. An ideal-security protocol for order-preserving encoding[C]. 2013 IEEE Symposium on Security and Privacy, Berkeley, USA, 2013: 463–477. VAN DIJK M, GENTRY C, HALEVI S, et al. Fully homomorphic encryption over the integers[C]. The 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, 2010: 24–43. -





 下载:
下载:



 下载:
下载:
