Distributed LT Codes on Multiple Layers Networks
-
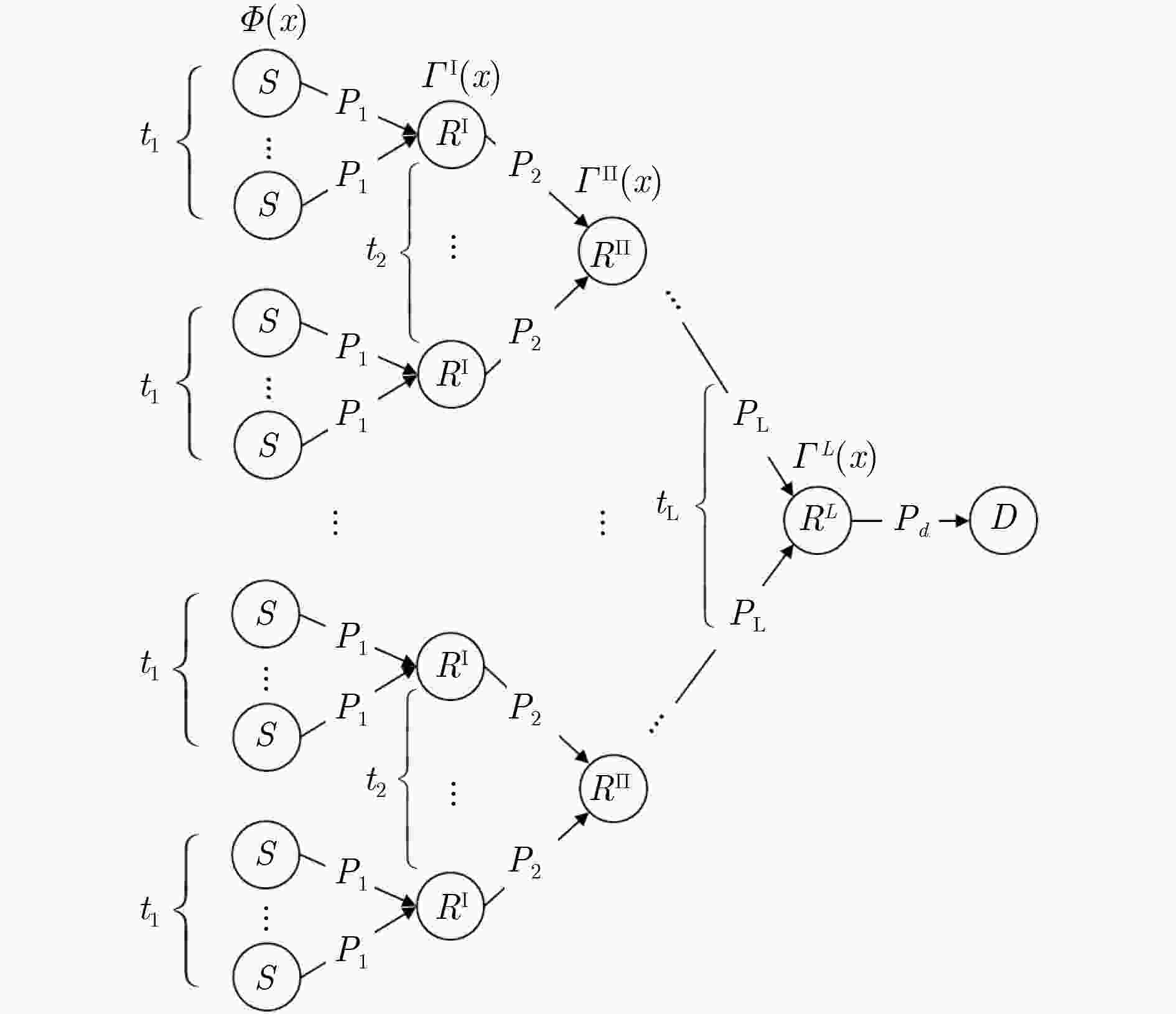
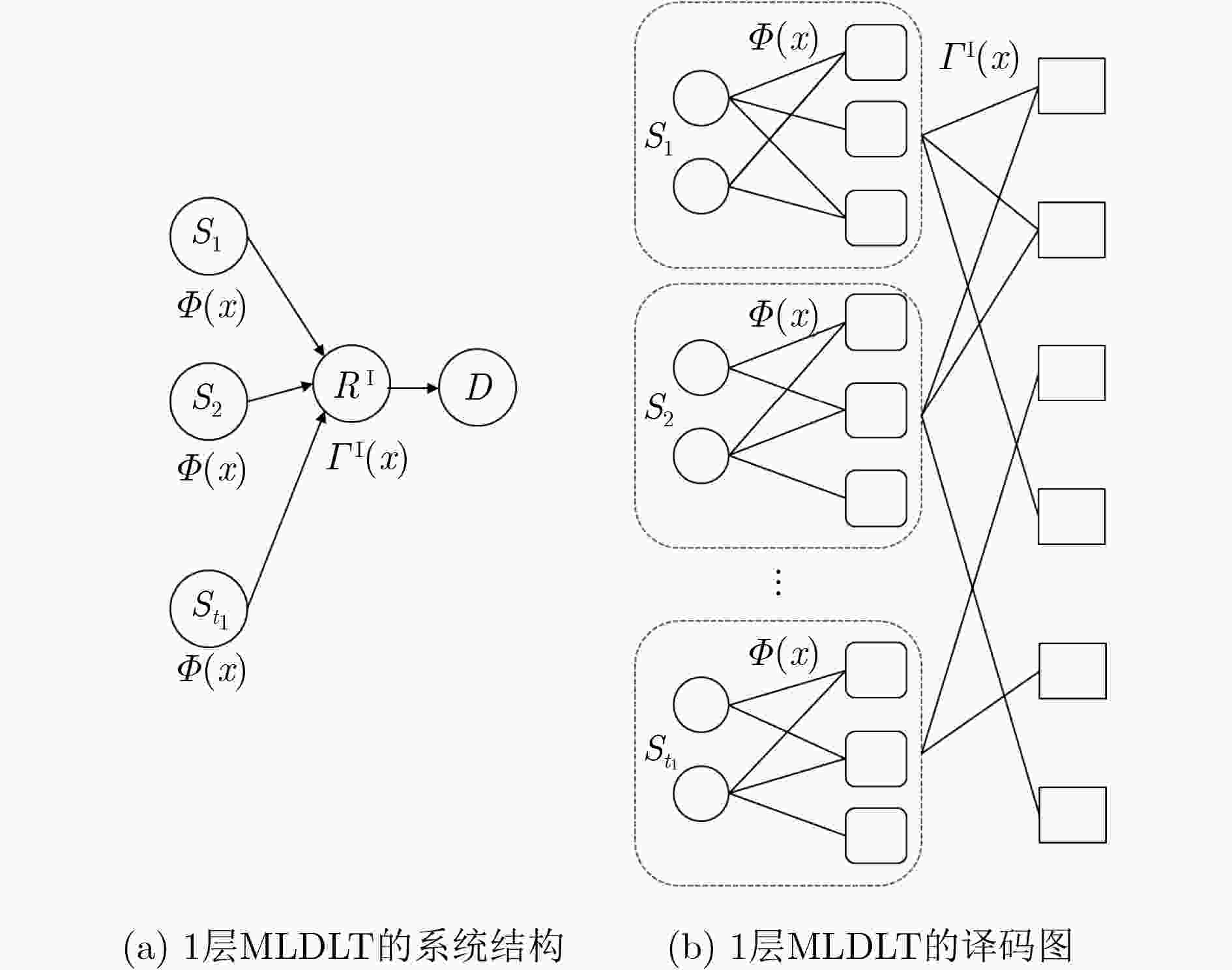
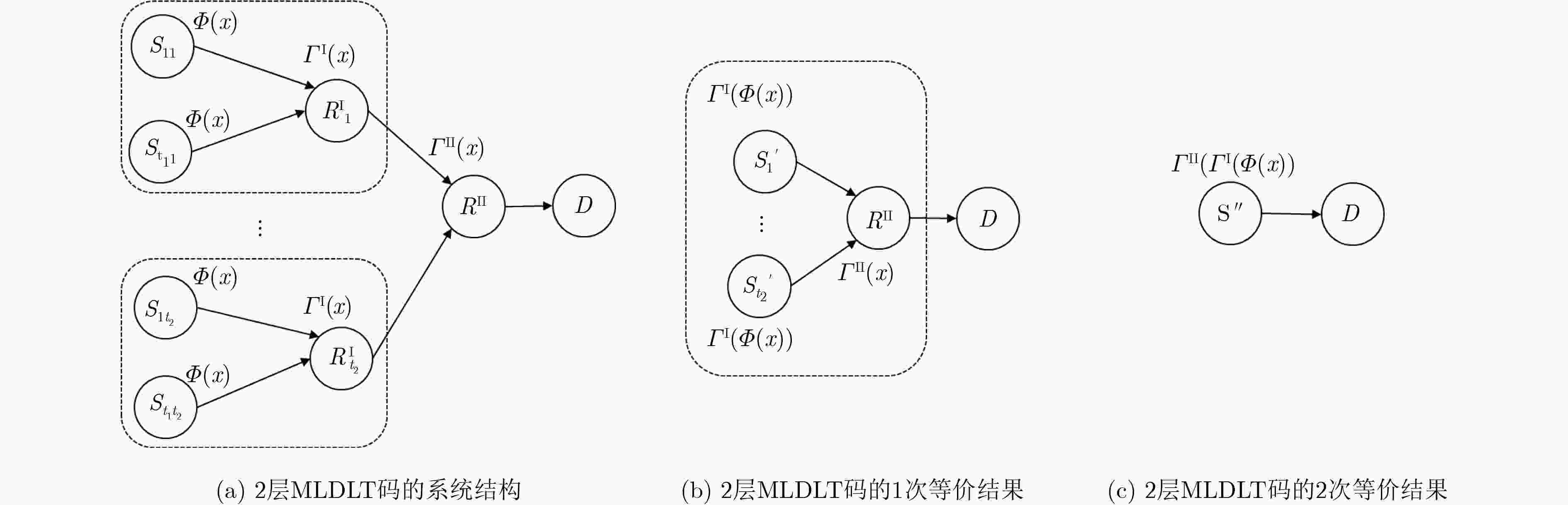
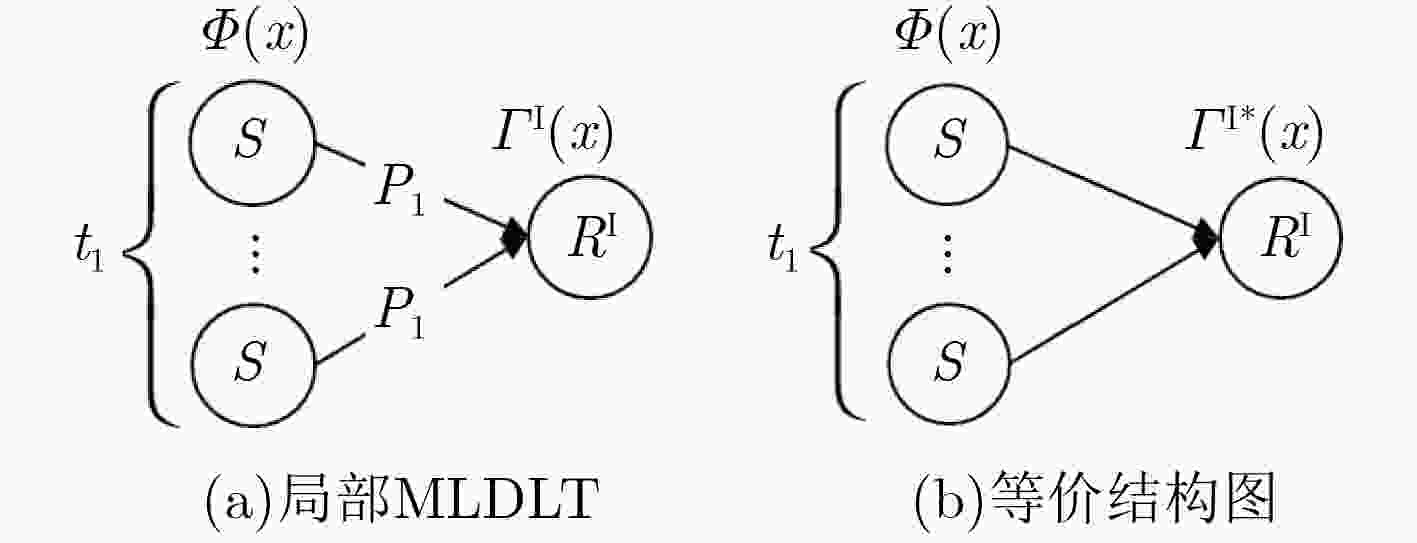
摘要: 目前对分布式LT码(DLT)的研究仅限于信源数量较少、且只有1层中继的情况,该文提出一种能够部署在多层中继网络上的分布式LT码,即多层分布式LT码(MLDLT)。该码将信源进行分组,将中继进行分层,通过分层后的中继群,可以将多达几十个乃至上百个信源连接到同一个接收端,从而实现众多信源通过多层中继对同一个接收终端的分布式LT码通信。通过对MLDLT码进行与或树分析,得出其中继度分布的线性优化方程。分别在无损和有损链路上计算该码的渐进性能并进行数值仿真,结果证明MLDLT码在无损和有损链路上的错误平台都比较低。MLDLT码非常适合于信源数量较多的多层中继网络。Abstract: Present researches on Distributed Luby’s Transmission (DLT) codes are restricted on several-sources and one-layer-relay networks, thus the Multiple Layers Distributed LT (MLDLT) code for multiple-layers-relays networks is proposed. In MLDLT, sources are grouped and realys are layered in order that scores of sources can be connected to the only destination through the layered relays. By this scheme, the distributed communication between scores of sources and the destination can be performed. Through the and-or tree analysis, the linear procedures for the optimization of the relays' degree distributions are derived. On both lossless and lossy links, asymptotic performances of MLDLT are analized and the numberical simulations are experimented. The results demonstrate that MLDLT can achieve satisfying erasure floors on both lossless and lossy links. MLDLT is a feasible solution for the scores-sources and multiple-layers-realys networks.
-
表 1 中继选择和编码算法
步骤1 从${t_1}$条链路上接收0级编码包; 步骤2 统计实际接收到的0级编码包数量$t_1^*$; 步骤3 中继$R_{}^{\rm{I}}$以概率$\varGamma _h^{\rm{I}}$选择度数$h$; 步骤4 if $t_1^* > h$ then 从$t_1^*$个0级编码包中任选$h$个进行混合; else then 将$t_1^*$个0级编码包进行混合。 end if 表 2
${\text{Γ}^{\text{I}}}\text{(}\text{x}\text{)}$ 和${\text{Γ}^{{\text{II}}}}\text{(}\text{x}\text{)}$ 的线性规划结果T=50 ${\varGamma ^{\rm{I}}}(x)$ 0.7101x+0.2899x5 ${\varGamma ^{{\rm{II}}}}(x)$ 0.8850x+0.0117x2 + 0.1033x10 T=100 ${\varGamma ^{\rm{I}}}(x)$ 0.7101x+0.2899x5 ${\varGamma ^{{\rm{II}}}}(x)$ 0.8625x+0.0534x2+0.0841x20 -
BYERS J W, LUBY M, MITZENMACHER M, et al. A digital fountain approach to reliable distribution of bulk data[J]. ACM Sigcomm Computer Communication, 1998, 28(4): 56–67. doi: 10.1145/285243.285258 索龙龙, 张更新, 边东明, 等. 高斯消元译码下LT码性能分析[J]. 计算机应用, 2018, 38(7): 2015–2019. doi: 10.11772/j.issn.1001-9081.2017122989SUO Longlong, ZHANG Gengxin, BIAN Dongming, et al. Performance analysis of Luby transform codes under Gaussian elimination decoding[J]. Journal of Computer Applications, 2018, 38(7): 2015–2019. doi: 10.11772/j.issn.1001-9081.2017122989 LUBY M. LT codes[C]. Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, Canada, 2002: 271–280. ALBAYRAK C and TURK K. Reduced-complexity decoding of LT codes[J]. Wireless Personal Communications, 2017, 94(3): 969–975. doi: 10.1007/s11277-016-3660-7 PUDUCHERI S, KLIEWER J, and FUJA T E. The design and performance of distributed LT codes[J]. IEEE Transactions on Information Theory, 2007, 53(10): 3740–3754. doi: 10.1109/TIT.2007.904982 LIAU A, YOUSEFI S, and KIM I M. Binary soliton-like rateless coding for the Y-network[J]. IEEE Transactions on Communications, 2011, 59(12): 3217–3222. doi: 10.1109/TCOMM.2011.091911.100189 LIAU A, KIM I M, and YOUSEFI S. Improved low-complexity soliton-like network coding for a resource-limited relay[J]. IEEE Transactions on Communications, 2013, 61(8): 3327–3335. doi: 10.1109/TCOMM.2013.061913.110585 SEJDINOVIC D, PIECHOCKI R J, and DOUFEXI A. And-or tree analysis of distributed LT codes[C]. Proceedings of the 2009 IEEE Information Theory Workshop on Networking and Information Theory, Volos, Greece, 2009: 261–265. HUSSAIN I, XIAO Ming, and RASMUSSEN L K. Buffer-based distributed LT codes[J]. IEEE Transactions on Communications, 2014, 62(11): 3725–3739. doi: 10.1109/TCOMM.2014.2362111 YANG Haitao, JIANG Ming, SHEN Hong, et al. A distributed LT code design for multiple-access relay networks subject to erasures[J]. IEEE Communications Letters, 2015, 19(4): 509–512. doi: 10.1109/LCOMM.2015.2398412 FEI Zesong, CAO Congzhe, XIAO Ming, et al. Improved LT codes in low overhead regions for binary erasure channels[J]. Transactions on Emerging Telecommunications Technologies, 2016, 27(1): 84–91. doi: 10.1002/ett.2798 LIAO Jianxin, ZHANG Lei, LI Tonghong, et al. A generalized design of distributed rateless codes with decreasing ripple size for multiple-access relay networks[J]. Wireless Networks, 2017, 23(7): 2177–2188. doi: 10.1007/s11276-016-1279-y XU Shengkai and XU Dazhuan. Design of degree distributions for finite length LT codes[J]. Wireless Personal Communications, 2018, 98(2): 2251–2260. doi: 10.1007/s11277-017-4972-y LUBY M G, MITZENMACHER M, and AMIN SHOKROLLAHI M. Analysis of random processes via and-or tree evaluation[C]. Proceedings of the Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, USA, 1998: 364–373. SUO Longlong, ZHANG Gengxin, LÜ Jing, et al. Performance analysis for finite length LT codes via classical probability evaluation[J]. IEEE Communications Letters, 2017, 21(9): 1957–1960. doi: 10.1109/LCOMM.2017.2700303 华洁, 徐大专, 许生凯. 系统LT码在删除信道下的渐进性能分析及度分布设计[J]. 数据采集与处理, 2017, 32(5): 906–912. doi: 10.16337/j.1004-9037.2017.05.007HUA Jie, XU Dazhuan, and XU Shengkai. Asymptotic performance analysis and degree distribution design for systematic Luby transform codes over binary erasure channel[J]. Journal of Data Acquisition and Processing, 2017, 32(5): 906–912. doi: 10.16337/j.1004-9037.2017.05.007 AHLSWEDE R, CAI Ning, LI S Y R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204–1216. doi: 10.1109/18.850663 LI S Y R, YEUNG R W, and CAI Ning. Linear network coding[J]. IEEE Transactions on Information Theory, 2003, 49(2): 371–381. doi: 10.1109/TIT.2002.807285 孔博, 张更新, 张威, 等. 空间信息网络中基于LT码的分布式存储策略[J]. 电子与信息学报, 2016, 38(4): 787–794. doi: 10.11999/JEIT150674KONG Bo, ZHANG Gengxin, ZHANG Wei, et al. Distributed storage strategy based on LT codes in space information network[J]. Journal of Electronics &Information Technology, 2016, 38(4): 787–794. doi: 10.11999/JEIT150674 -





 下载:
下载:




 下载:
下载:
