Eliminating Structural Redundancy Based on Super-node Theory
-
摘要: 本体作为指导知识图谱数据构建的上层结构,在知识图谱技术中具有重要意义。本体在发展的过程中会形成结构上的冗余。现有的本体消冗方法无法处理含有等价关系的本体结构,只能针对单一类属关系进行冗余的检测与消除。该文针对含有等价关系的本体提出一种基于超节点理论的消冗算法,首先将相互等价的节点看作超节点,消除单一类属关系之间的的冗余;然后还原等价节点,消除等价关系与类属关系之间的冗余。在计算机生成网络和真实网络上的实验和分析表明,该算法能够准确识别关系冗余,具有较高的稳定性和综合性能。Abstract: Ontology, as the superstructure of knowledge graph, has great significance in knowledge graph domain. In general, structural redundancy may arise in ontology evolution. Most of existing redundancy elimination algorithms focus on transitive redundancies while ignore equivalent relations. Focusing on this problem, a redundancy elimination algorithm based on super-node theory is proposed. Firstly, the nodes equivalent to each other are considered as a super-node to transfer the ontology into a directed acyclic graph. Thus the redundancies relating to transitive relations can be eliminated by existing methods. Then equivalent relations are restored, and the redundancies between equivalent and transitive relations are eliminated. Experiments on both synthetic dynamic networks and real networks indicate that the proposed algorithm can detect redundant relations precisely, with better performance and stability compared with the benchmarks.
-
Key words:
- Ontology /
- Equivalent relation /
- Super node /
- Relation redundancy /
- Transitive relationship
-
表 1 消冗算法伪代码
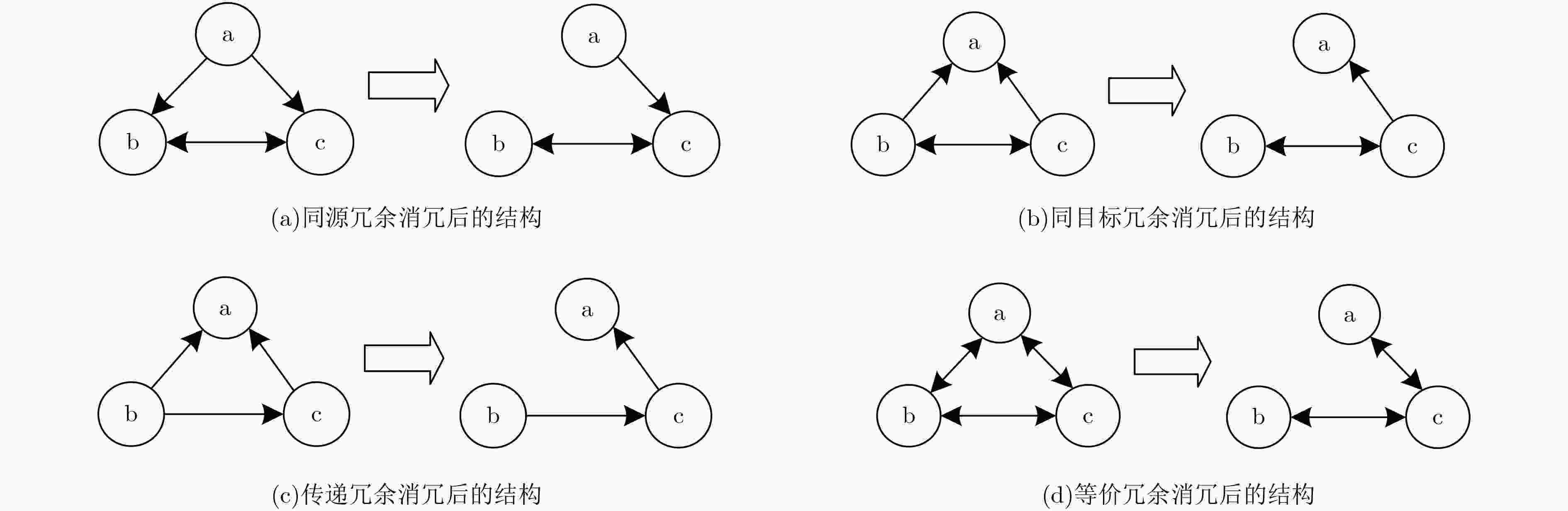
输入:本体网络${\text{M}}$ 输出:消冗后的本体网络${\text{R}}$ (1) /*超节点的转化*/ (2) ${\text{Me}} \leftarrow $$t({\text{M}} \!\otimes\! {{\text{M}}^{\rm{T}}})$/*抽取本体网络中的等价关系,存入${\text{Me}}$*/
(3) ${{\rm Mr}_{ij}} \leftarrow $${\rm{bool}}\left(\sum\nolimits_k {({M_{ik}} \cdot {\rm{M}}{{\rm{e}}_{kj}}} + {\rm{M}}{{\rm{e}}_{ik}} \cdot {M_{kj}})\right) - {\rm{M}}{{\rm{e}}_{ij}}$/*将等价 关系转化为类属关系*/(4) /*传递冗余的消除*/ (5) ${\text{R}} \leftarrow {\text{Mr}}$ (6) $D[V\;],I[V\;] = \rm{FEDRR} (G(V,E))$/*用FEDRR算法求出网络中 每个节点的孩子集合$D[V\;]$与后代集合$I[V\;]$*/ (7) for all $v \in V\;$ do (8) for all $s \in I[v] \cap D[v]$ do (9) delete $(s,v,R)$/*置${R_{sv}} = 0$*/ (10) end for (11) end for (12) /*等价-类属冗余的消除*/ (13) ${\text{E}} \leftarrow $${\rm{Equiv(}}{\text{Me}}{\rm{)}}$/*$E$每行表示一种等价关系*/ (14) ${S_{ij}} = {\rm{bool}}\left(\sum\nolimits_k {{E_{ik}} \cdot {R_{jk}} - 1} \right)$/*构造同源冗余*/ (15) ${T_{ij}} = {\rm{bool}}\left(\sum\nolimits_k {{E_{ik}} \cdot {R_{kj}} - 1} \right)$/*构造同目标冗余*/ (16) for $i$ from 1 to n do/*去除矩阵中等价关系与偏序关系之间 的冗余,n是矩阵大小*/ (17) for $j$ from 1 to n do (18) if ${S_{ij}} > 1$ then/*去除同源冗余*/ (19) $\rm{Elim} \_Line({\text{E}}.{\rm{row}} (i),{\text{R}}.{\rm row}(j))$/*只保留节点$j$到 超节点$i$的一条边*/ (20) end if (21) if ${T_{ij}} > 1$ then/*去除同目标冗余*/ (22) ${\rm{Elim\_Line}}({\text{E}}.{\rm{row}}(i),{\text{R}}.{\rm column}(j))$/*只保留超节点 $i$到节点$j$的一条边*/ (23) end if (24) end for (25) end for (26) /*恢复等价关系*/ (27) ${R_{ij}} \leftarrow {\rm{bool}}({R_{ij}} + {\rm{M}}{{\rm{e}}_{ij}})$ 表 2 随机生成网络配置参数
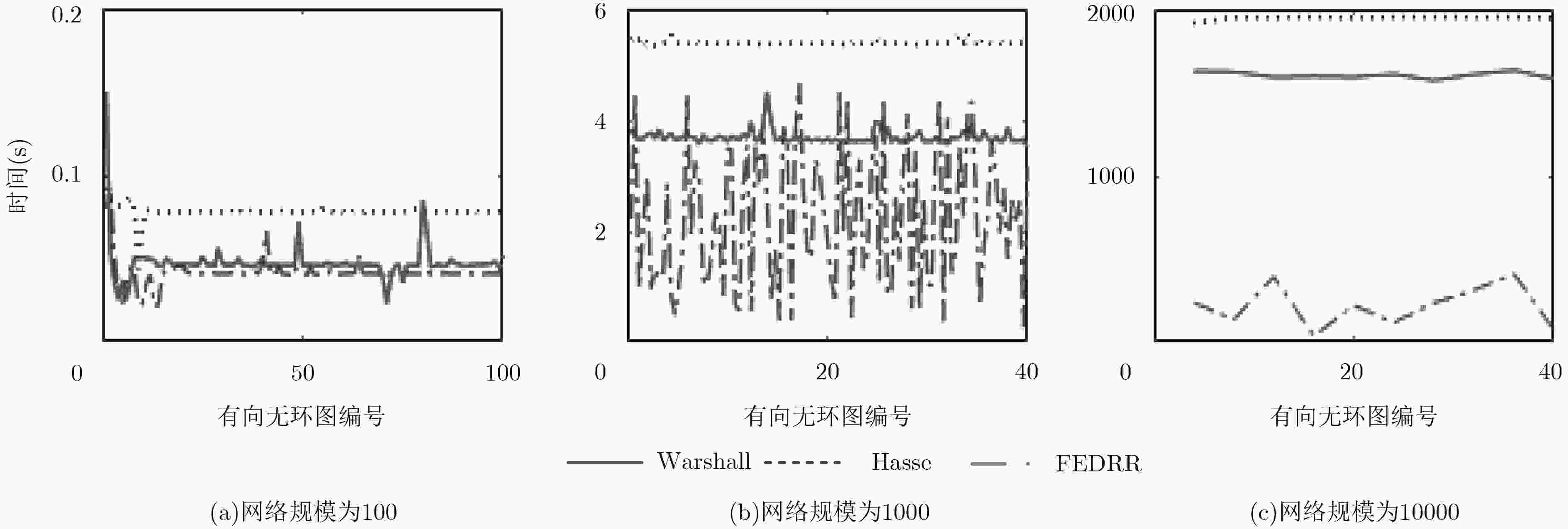
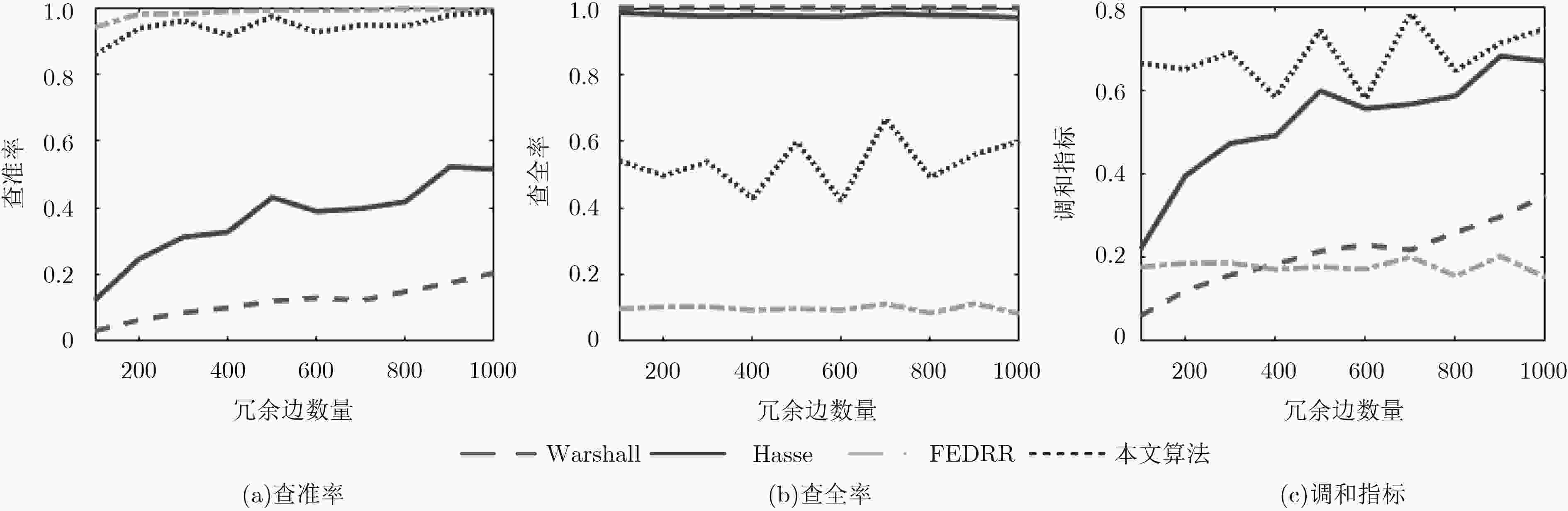
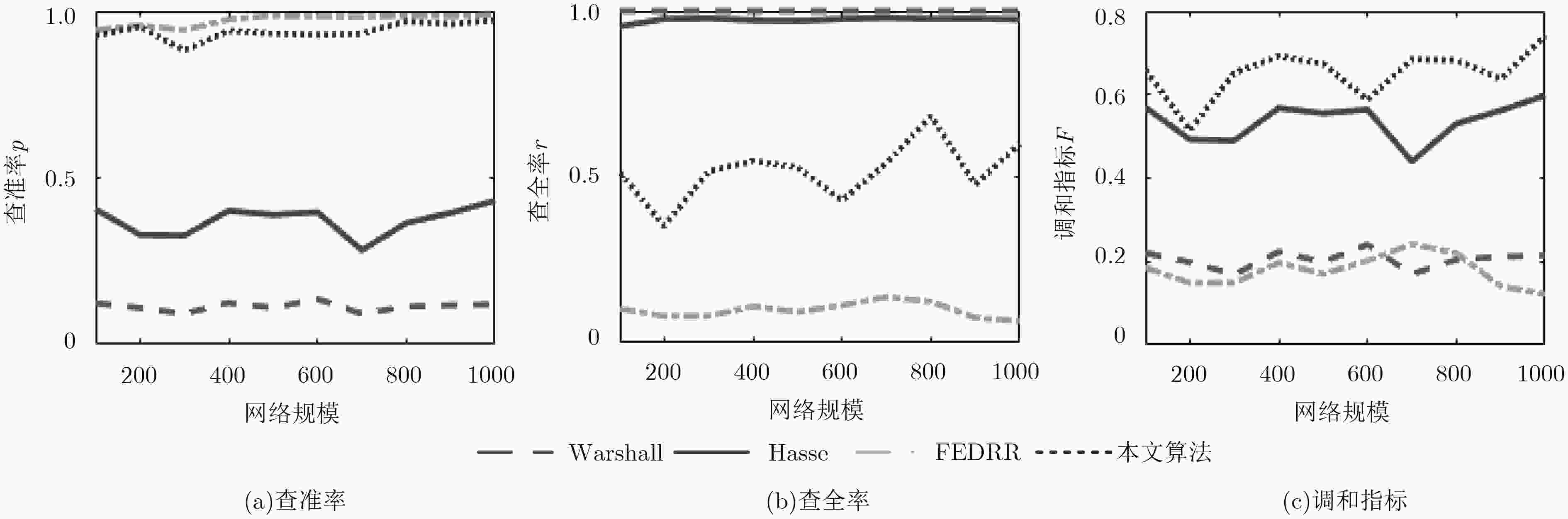
网络规模$N$ 网络个数$n$ 最大等价节点对数 冗余边数 配置1 1000 100 500 (100,1000) 配置2 (100,1000) 100 0.5$N$ (1,$N$) -
刘峤, 李杨, 段宏, 等. 知识图谱构建技术综述[J]. 计算机研究与发展, 2016, 53(3): 582–600. doi: 10.7544/issn1000-1239.2016.20148228LIU Qiao, LI Yang, DUAN Hong, et al. Knowledge graph construction techniques[J]. Journal of Computer Research and Development, 2016, 53(3): 582–600. doi: 10.7544/issn1000-1239.2016.20148228 BORO D and BHUYAN Z. A game for shared ontology evolution[C]. Proceedings of the International Conference on Computing and Communication Systems, Shillong, India, 2018: 95–101. 刘树新, 季新生, 刘彩霞, 等. 局部拓扑信息耦合促进网络演化[J]. 电子与信息学报, 2016, 38(9): 2180–2187. doi: 10.11999/JEIT151338LIU Shuxin, JI Xinsheng, LIU Caixia, et al. Information coupling of local topology promoting the network evolution[J]. Journal of Electronics &Information Technology, 2016, 38(9): 2180–2187. doi: 10.11999/JEIT151338 XING Guangming, ZHANG Guoqiang, and CUI Licong. FEDRR: Fast, exhaustive detection of redundant hierarchical relations for quality improvement of large biomedical ontologies[J]. BioData Mining, 2016, 9: 31–42. doi: 10.1186/s13040-016-0110-8 DENTLER K and CORNET R. Intra-axiom redundancies in SNOMED CT[J]. Artificial Intelligence in Medicine, 2015, 65(1): 29–34. doi: 10.1016/j.artmed.2014.10.003 于娟, 熊振辉, 欧忠辉. 基于哈斯图的本体偏序关系消冗方法研究[J]. 情报学报, 2015, 34(3): 279–285. doi: 10.3772/j.issn.1000-0135.2015.003.006YU Juan, XIONG Zhenhui, and OU Zhonghui. Eliminating redundant ontology relations based on Hasse Diagram[J]. Journal of the China Society for Scientific and Technical Information, 2015, 34(3): 279–285. doi: 10.3772/j.issn.1000-0135.2015.003.006 OCHS C, PERL Y, GELLER J, et al. An empirical analysis of ontology reuse in BioPortal[J]. Journal of Biomedical Informatics, 2017, 71: 165–177. doi: 10.1016/j.jbi.2017.05.021 SHARP M E. Toward a comprehensive drug ontology: Extraction of drug-indication relations from diverse information sources[J]. Journal of Biomedical Semantics, 2017, 8: 2–12. doi: 10.1186/s13326-016-0110-0 CHATTERJEE N, KAUSHIK N, GUPTA D, et al. Ontology merging: A practical perspective[J]. Information and Communication Technology for Intelligent Systems, 2018: 136–145. doi: 10.1007/978-3-319-63645-0_15 JHA M, VELTRI P, GUZZI P H, et al. Network based algorithms for module extraction from RNASeq data: A quantitative assessment[C]. Proceedings of 2017 IEEE International Conference on Bioinformatics and Biomedicine, Kansas City, USA, 2017: 1312–1315. DORAN P, TAMMA V, and IANNONE L. Ontology module extraction for ontology reuse: An ontology engineering perspective[C]. Proceedings of the Sixteenth ACM Conference on Conference on Information and Knowledge Management, Lisbon, Portugal, 2007: 61–70. ABEYSINGHE R, HINDERER E W, MOSELEY H N B, et al. Auditing subtype inconsistencies among gene ontology concepts[C]. Proceedings of 2017 IEEE International Conference on Bioinformatics and Biomedicine, Kansas City, USA, 2017: 1242–1245. DIETZE F, VALDEZ A C, KAROFF J, et al. That’s so meta! Usability of a hypergraph-based discussion model[C]. Proceedings of the 8th International Conference on Digital Human Modeling. Applications in Health, Safety, Ergonomics, and Risk Management: Health and Safety, Vancouver, Canada, 2017: 248–258. WARSHALL S. A theorem on boolean matrices[J]. Journal of the ACM (JACM) , 1962, 9(1): 11–12. doi: 10.1145/321105.321107 刘树新, 季新生, 刘彩霞, 等. 一种信息传播促进网络增长的网络演化模型[J]. 物理学报, 2014, 63(15): 158902. doi: 10.7498/aps.63.158902LIU Shuxin, JI Xinsheng, LIU Caixia, et al. A complex network evolution model for network growth promoted by information transmission[J]. Acta Physica Sinica, 2014, 63(15): 158902. doi: 10.7498/aps.63.158902 徐雷. 本体网络结构及其演化研究[D]. [博士论文], 武汉大学, 2014.XU Lei. A research on the structure of ontology networks and its evolution[D]. [Ph.D. dissertation], Wuhan University, 2014. RASKIN R G and PAN M J. Knowledge representation in the semantic web for Earth and environmental terminology (SWEET)[J]. Computers & Geosciences, 2005, 31(9): 1119–1125. doi: 10.1016/j.cageo.2004.12.004 SAVIĆ M, IVANOVIĆ M, and JAIN L C. Complex Networks in Software, Knowledge, and Social Systems[M]. Cham: Springer, 2019: 143–175. -





 下载:
下载:

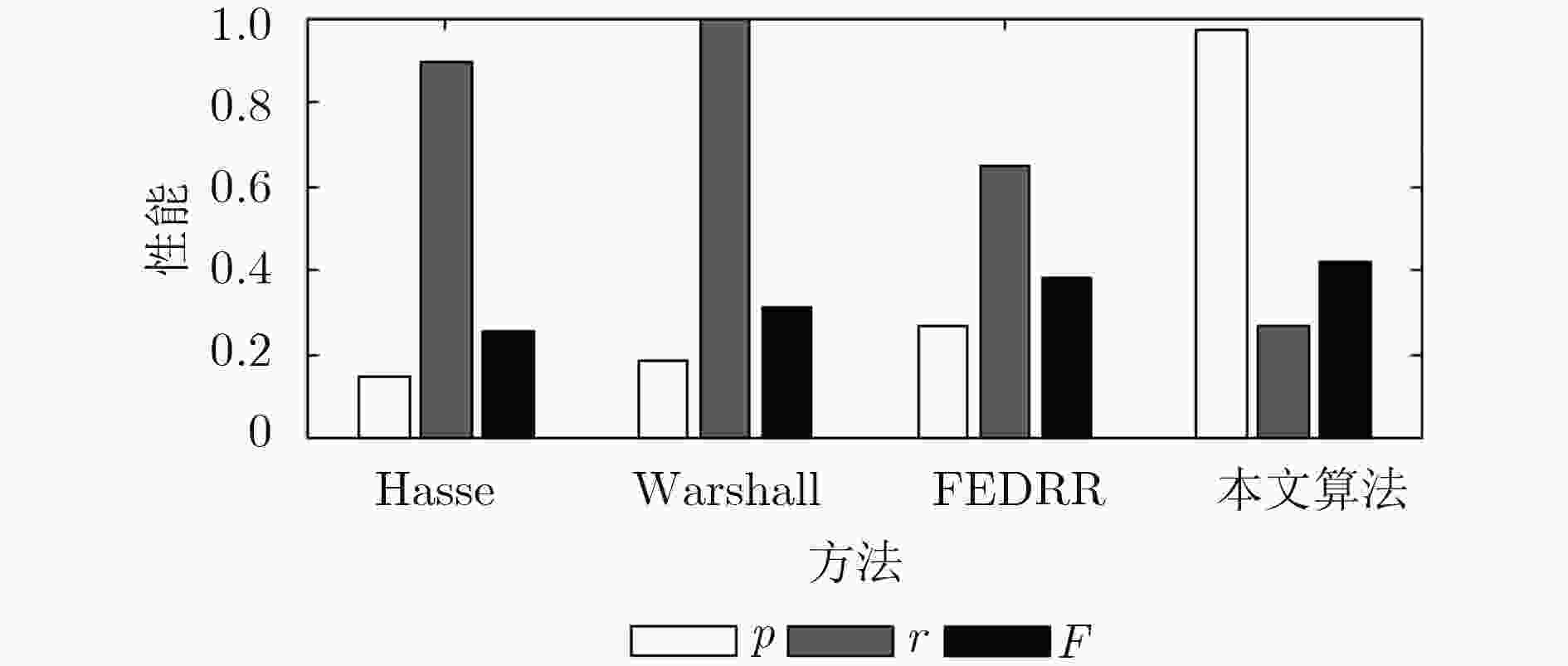


 下载:
下载:
