Joint User Association and Power Allocation Algorithm for Network Slicing Based on NOMA
-
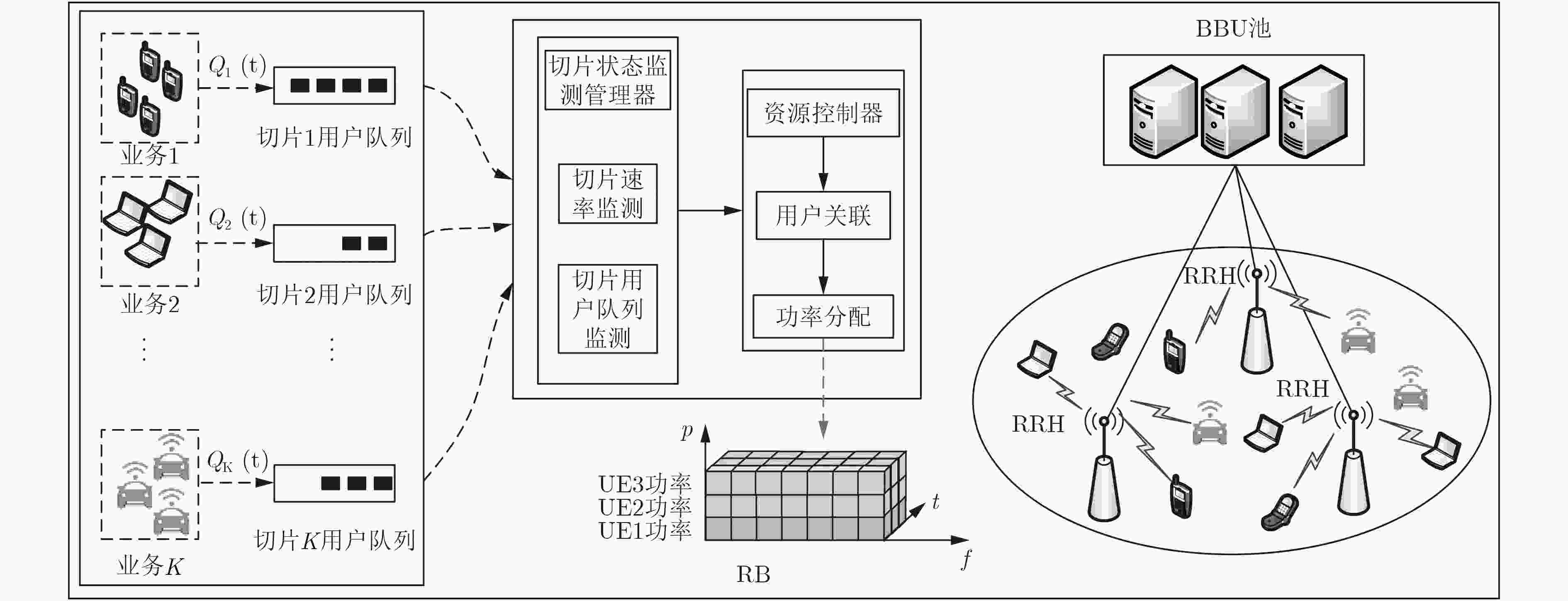
摘要: 为了满足网络切片多样化需求,实现无线虚拟资源的动态分配,该文提出在C-RAN架构中基于非正交多址接入的联合用户关联和功率资源分配算法。首先,该算法考虑在不完美信道条件下,以切片和用户最小速率需求及时延QoS要求、系统中断概率、前传容量为约束,建立在C-RAN场景中最大化长时平均网络切片总吞吐量的联合用户关联和功率分配模型。其次,将概率混合优化问题转换为非概率优化问题,并利用Lyapunov优化理论设计一种基于当前时隙的联合用户调度和功率分配的算法。最后采用贪婪算法求得用户关联问题次优解;基于用户关联的策略,将功率分配的问题利用连续凸逼近方法将其转换为凸优化问题并采用拉格朗日对偶分解方法获得功率分配策略。仿真结果表明,该算法能满足各网络切片和用户需求的同时有效提升系统时间平均切片总吞吐量。Abstract: To satisfy the diversity of requirements for different network slices and realize dynamic allocation of wireless virtual resource, an algorithm for network slice joint user association and power allocation is proposed in Non-Orthogonal Multiple Access(NOMA) C-RAN. Firstly, by considering imperfect Channel State Information(CSI), a joint user association and power allocation algorithm is designed to maximize the average total throughput in C-RAN with the constraints of slice and user minimum required rate, outage probability and fronthaul capacity limits. Secondly, a joint user association and power allocation algorithm is designed according to the current slot by transforming the probabilistic mixed optimalization problem into a non-probabilistic optimalization problem and using Lyapunov optimization. Finally, for user association problem, a greedy algorithm is proposed to find a feasible suboptimal solution; The power allocation problem is transformed into a convex optimization problem by using successive convex approximation; Then a dual decomposition approach is exploited to obtain a power allocation strategy. Simulation results demonstrate that the proposed algorithm can effectively improve the average total throughput of system while guaranteeing the network slice and user requirement.
-
表 1 仿真参数
参数 数值 RB数量 35 RB最大复用用户数 3 RB带宽 180 kHz RRH功率$p_l^{\max }$ 30 dBm fronthaul容量${ {{C} }_{l, \max } }$ 100 Mb/s 切片用户最低速率需求 500 kb/s, 1 Mb/s, 2 Mb/s 用户数据包到达率 3 packets/slot 路径损耗衰落模型 157.4+32lg(d)(d[km]) 噪声功率谱密度${N_0}$ –174 dBm/Hz 时隙长度,$\sigma _e^2$, ${\varepsilon _{\rm out}}$ 5 ms, 0.05, 0.10 -
LIU Gang, YU F R, JI Hong, et al. Distributed resource allocation in virtualized full-duplex relaying networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 8444–8460. doi: 10.1109/TVT.2015.2513070 YIN Lei, QIU Ling, and CHEN Zheng. Throughput-maximum resource provision in the OFDMA-based wireless virtual network[C]. IEEE 85th Vehicular Technology Conference (VTCSpring), Sydney, Australia, 2017: 1–6. doi: 10.1109/VTCSpring.2017.8108502. SINAIE M, NG D W K, and JORSWIECK E A. Resource allocation in NOMA virtualized wireless networks under statistical delay constraints[J]. IEEE Wireless Communications Letters, 2018, 7(6): 954–957. doi: 10.1109/LWC.2018.2841852 DAWADI R, PARSAEEFARD S, DERAKHSHANI M, et al. Power-efficient resource allocation in NOMA virtualized wireless networks[C]. IEEE Global Communications Conference (GLOBECOM), Washington, USA, 2016: 1–6. doi: 10.1109/GLOCOM.2016.7842162. LEE Y L, LOO J, CHUAH T C, et al. Dynamic network slicing for multitenant heterogeneous cloud radio access networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2146–2161. doi: 10.1109/TWC.2017.2789294 HA V N and LE L B. End-to-end network slicing in virtualized OFDMA-based cloud radio access networks[J]. IEEE Access, 2017, 5: 18675–18691. doi: 10.1109/ACCESS.2017.2754461 IKKI S S and AISSA A. Two-way amplify-and-forward relaying with Gaussian imperfect channel estimations[J]. IEEE Communications Letters, 2012, 16(7): 956–959. doi: 10.1109/LCOMM.2012.050912.120103 WANG Xiaoming, ZHENG Fuchun, ZHU Pengcheng, et al. Energy-efficient resource allocation in coordinated downlink multicell OFDMA systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(3): 1395–1408. doi: 10.1109/TVT.2015.2413950 XIANG Xudong, LIN Chuang, CHEN Xin, et al. Toward optimal admission control and resource allocation for LTE-A femtocell uplink[J]. IEEE Transactions on Vehicular Technology, 2015, 64(7): 3247–3261. doi: 10.1109/TVT.2014.2351837 PAPANDRIOPOULOS J and EVANS J S. SCALE: A low-complexity distributed protocol for spectrum balancing in multiuser DSL networks[J]. IEEE Transactions on Information Theory, 2009, 55(8): 3711–3724. doi: 10.1109/TIT.2009.2023751 FOOLADIVANDA D and ROSENBERG C. Joint resource allocation and user association for heterogeneous wireless cellular networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(1): 248–257. doi: 10.1109/TWC.2012.121112.120018 ZHU Jianyue, WANG Jiaheng, HUANG Yongming, et al. On optimal power allocation for downlink non-orthogonal multiple access systems[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(12): 2744–2757. doi: 10.1109/JSAC.2017.2725618 PARIDA P and DAS S S. Power allocation in OFDM based NOMA systems: A DC programming approach[C]. IEEE GLOBECOM Workshops, Austin, USA, 2015: 1026–1031. -





 下载:
下载:


 下载:
下载:
