|
XU Luzhou, LI Jian, and STOICA P. Target detection and parameter estimation for MIMO radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 927–939. doi: 10.1109/TAES.2008.4655353
|
|
HAIMOVICH A M, BLUM R S, and CIMINI L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116–129. doi: 10.1109/MSP.2008.4408448
|
|
LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812
|
|
YAN Haidong, LI Jun, and LIAO Guisheng. Multitarget identification and localization using bistatic MIMO radar systems[J]. EURASIP Journal on Advances in Signal Processing, 2007, 2008: 283483. doi: 10.1155/2008/283483
|
|
DUOFANG C, BAIXIAO C, and GUODONG Q. Angle estimation using ESPRIT in MIMO radar[J]. Electronics Letters, 2008, 44(12): 770–771. doi: 10.1049/el:20080276
|
|
ZHENG Z D and ZHANG J Y. Fast method for multi-target localisation in bistatic MIMO radar[J]. Electronics Letters, 2011, 47(2): 138–139. doi: 10.1049/el.2010.2577
|
|
梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1): 80–89. doi: 10.11999/JEIT150402LIANG Hao, CUI Chen, and YU Jian. Reduced-dimensional DOA estimation based on ESPRIT algorithm in monostatic MIMO radar with cross array[J]. Journal of Electronics &Information Technology, 2016, 38(1): 80–89. doi: 10.11999/JEIT150402
|
|
张正言, 张剑云. 双基地MIMO雷达多目标高精度跟踪算法[J]. 系统工程与电子技术, 2018, 40(6): 1241–1248. doi: 10.3969/j.issn.1001-506X.2018.06.08ZHANG Zhengyan and ZHANG Jianyun. Multi-target high precision tracking algorithm for bistatic MIMO radar[J]. Systems Engineering and Electronics, 2018, 40(6): 1241–1248. doi: 10.3969/j.issn.1001-506X.2018.06.08
|
|
ZHENG Guimei, CHEN Baixiao, and YANG Minglei. Unitary ESPRIT algorithm for bistatic MIMO radar[J]. Electronics Letters, 2012, 48(3): 179–181. doi: 10.1049/el.2011.3657
|
|
HAARDT M and NOSSEK J A. Unitary ESPRIT: How to obtain increased estimation accuracy with a reduced computational burden[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1232–1242. doi: 10.1109/78.382406
|
|
CAI Changxin, WEN Fangqing, and HUANG Dongmei. New approach to angle estimation for bistatic MIMO radar with unknown spatially colored noise[J]. IEEE Access, 2018, 6: 24249–24255. doi: 10.1109/ACCESS.2018.2829537
|
|
张秦, 张林让, 郑桂妹, 等. 任意阵列双基地MIMO雷达的半实值MUSIC目标DOD和DOA联合估计[J]. 系统工程与电子技术, 2016, 38(3): 532–538. doi: 10.3969/j.issn.1001-506X.2016.03.09ZHANG Qin, ZHANG Linrang, ZHENG Guimei, et al. Joint DOD and DOA estimation for bistatic MIMO radar with arbitrary array using semi-real-valued MUSIC[J]. Systems Engineering and Electronics, 2016, 38(3): 532–538. doi: 10.3969/j.issn.1001-506X.2016.03.09
|
|
ZOLTOWSKI M D, HAARDT M, and MATHEWS C P. Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT[J]. IEEE Transactions on Signal Processing, 1996, 44(2): 316–328. doi: 10.1109/78.485927
|
|
HAARDT M, ROEMER F, and DEL GALDO G D. Higher-order SVD-based subspace estimation to improve the parameter estimation accuracy in multidimensional harmonic retrieval problems[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 3198–3213. doi: 10.1109/TSP.2008.917929
|
|
NION D and SIDIROPOULOS N D. A PARAFAC-based technique for detection and localization of multiple targets in a MIMO radar system[C]. Proceedings of 2009 IEEE International Conference on Acoustics, Speech and Signal, Taibei, China, 2009: 2077–2080.
|
|
XU Baoqing, ZHAO Yongbo, CHENG Zengfei, et al. A novel unitary PARAFAC method for DOD and DOA estimation in bistatic MIMO radar[J]. Signal Processing, 2017, 138: 273–279. doi: 10.1016/j.sigpro.2017.03.016
|
|
杨康, 文方青, 黄冬梅, 等. 基于实值三线性分解的互耦条件下双基地MIMO雷达角度估计算法[J]. 系统工程与电子技术, 2018, 40(2): 314–321. doi: 10.3969/j.issn.1001-506X.2018.02.12YANG Kang, WEN Fangqing, HUANG Dongmei, et al. Real-value-based trilinear decomposition-based direction estimation algorithm for bistatic MIMO radar in the presence of mutual coupling[J]. Systems Engineering and Electronics, 2018, 40(2): 314–321. doi: 10.3969/j.issn.1001-506X.2018.02.12
|
|
GRANT M and BOYD S. CVX: Matlab software for disciplined convex programming[EB/OL]. http://cvxr.com/cvx/, 2008.
|
|
FORSTER P and VEZZOSI G. Application of spheroidal sequences to array processing[C]. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal, Dallas, USA, 1987: 2268–2271. doi: 10.1109/ICASSP.1987.1169421.
|
|
HAARDT M and NOSSEK J A. Simultaneous Schur decomposition of several nonsymmetric matrices to achieve automatic pairing in multidimensional harmonic retrieval problems[J]. IEEE Transactions on Signal Processing, 1998, 46(1): 161–169. doi: 10.1109/78.651206
|
|
ZHANG X, XU Z, XU L, et al. Trilinear decomposition-based transmit angle and receive angle estimation for multiple-input multiple-output radar[J]. IET Radar, Sonar & Navigation, 2011, 5(6): 626–631. doi: 10.1049/iet-rsn.2010.0265
|





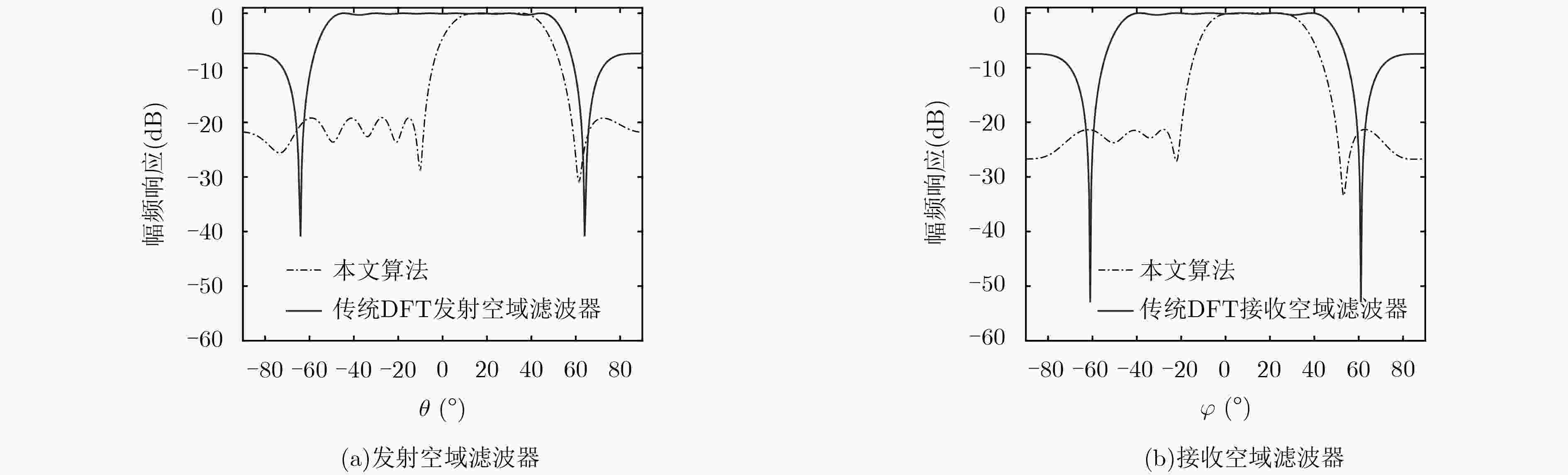
 下载:
下载:
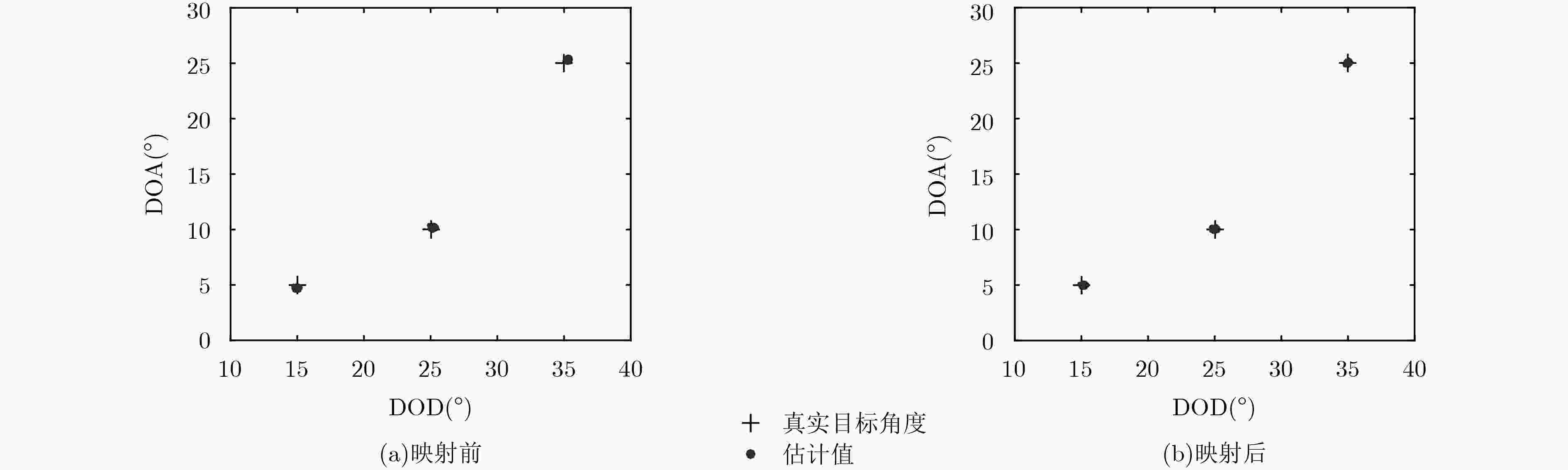
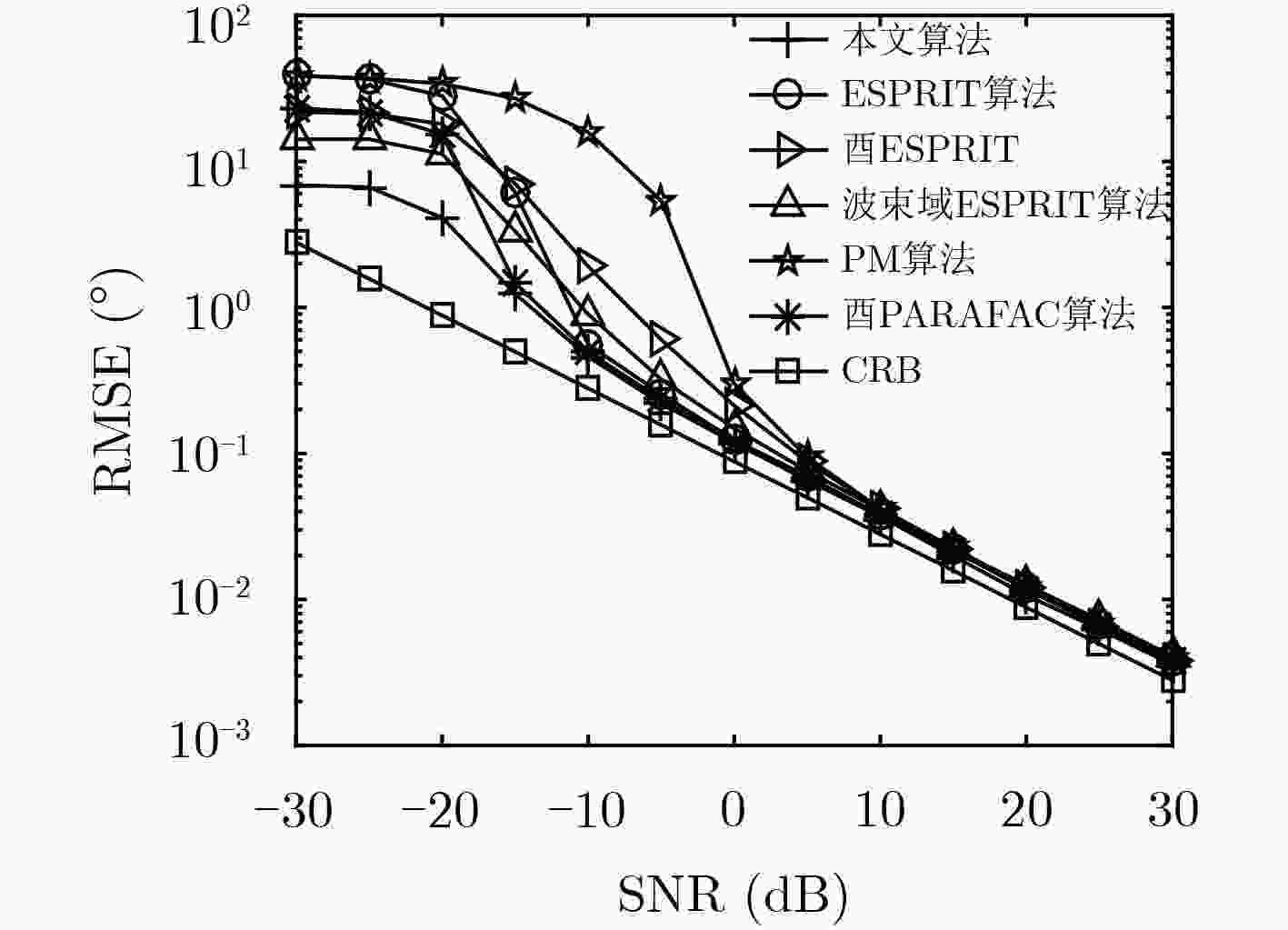
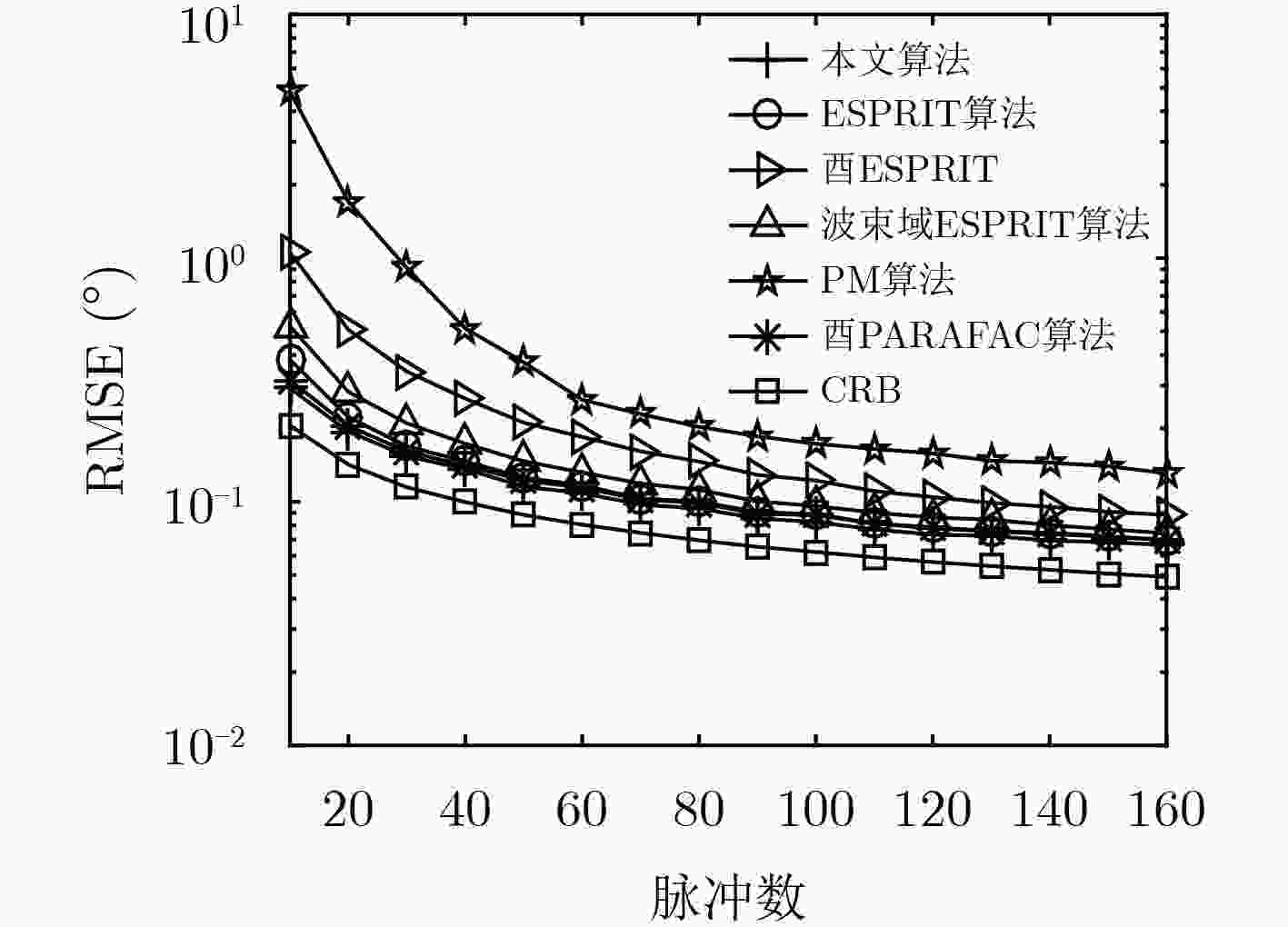


 下载:
下载:
