Generalized Adjacent Multi-beam Adaptive Processing Based Low-altitude Wind-shear Wind Speed Estimation under Aircraft Yawing
-
摘要: 该文提出一种载机偏航下基于广义相邻多波束(GMB)自适应处理的低空风切变风速估计的方法，该方法首先利用基于回波数据的杂波距离依赖性补偿方法对杂波进行距离依赖性矫正，估计出杂波协方差矩阵。然后同时组合空域的相邻多个波束与时域的相邻多个多普勒通道来计算降维变换矩阵，并对待测距离单元内的雷达回波数据进行降维处理，进而构造GMB自适应处理器的最优自适应权矢量对降维后的回波数据实现自适应滤波。最后完成载机偏航下风场速度的准确估计。仿真结果验证了该方法能够在载机偏航情况下，获得风场速度的有效估计。Abstract: This paper presents a method of low-altitude wind-shear speed estimation based on Generalized adjacent Multi-Beam (GMB) adaptive processing under aircraft yawing. The clutter range-dependence compensation method based on echo data is first used to correct the range dependence of clutter for estimating the clutter covariance matrix. Then the dimension-reduced transform matrix is calculated by combining adjacent multiple beams in the airspace and adjacent multiple Doppler channels in time domain simultaneously, and the radar echo data of the measured range bin is reduced in dimension, and then the optimal weight vector of the GMB adaptive processor is constructed to filter adaptively the dimension-reduced data. Finally, the accurate estimation of the wind speed under the aircraft yawing is got. The simulation results show that the proposed method can obtain an effective estimation of wind speed under aircraft yawing.
-
1. 引言
根据来自国际电信无线电通信部门的一份调研报告，不包含机器对机器(Machine to Machine, M2M)流量在内的移动流量在2020—2030年将以每年54%的速率增长，到2025年全球每个月的移动流量将达到543 EB，到2030年将达到4394 EB[1]。移动数据流量的急剧增长给移动通信网络带来了巨大压力，使得未来移动通信系统的业务服务质量受到了极大挑战。为了获得更好的用户体验、更高的通信速率和更大的系统容量，第3代合作伙伴计划(3rd Generation Partnership Project, 3GPP)提出了工作在5 GHz免授权频段的长期演进(Long Term Evolution, LTE)技术，也称为LTE授权辅助接入(Licensed Assisted Access, LAA)。因为授权频谱相当匮乏，且成本高昂，LAA将利用5 GHz免授权频段来辅助主载波进行下行链路数据的传输[2]。为了确保与WiFi系统在5 GHz免授权频段上的公平共存，LAA采用了与WiFi的具有碰撞避免的载波侦听多路访问(Carrier Sense Multiple Access/Collision Avoidance, CSMA/CA)相似的信道接入机制来增强共存系统的碰撞避免能力[3]。
目前在LAA网络中存在4种信道接入方案[4,5]：Category (Cat)-1, cat-2, cat-3 and cat-4。3GPP还为具有随机退避的下行先听后说(Listen Before Talk, LBT)定义了4种不同的优先级等级，每种等级在竞争窗口和不同的最大信道占用时间(Maximum Channel Occupancy Time, MCOT)上使用不同的最小值和最大值。对于优先等级3和4，如果存在共享载波的任何其他技术[4-6]，则MCOT为8 ms。
尽管LTE-LAA可以极大地提高每个用户的吞吐量并进一步显著改善用户的体验，但它也可能对 WiFi用户产生不利的影响。出于这些担忧，人们对LAA和WiFi网络的共存性能进行了广泛的研究[2,4]。然而，这些工作忽略了捕获效应，捕获效应是一种当两个以上的信号在相同信道上同时传输时，最强的信号仍可能被成功接收的现象，并且这种现象在共存场景中可能比在WiFi网络中更频繁地发生。
一般认为，当来自LAA和WiFi网络的两个以上信号通过相同信道同时传输时，由于传输冲突，无法成功接收信号。然而，在现实中，如果一个信号和其他信号之间的功率差大于某个阈值，则该信号仍然可以成功完成传输。这种现象称为捕获效应。显然，如果不考虑捕获效应，评估的共存性能可能会产生很大的偏差，无法准确反映实际情况，尤其是在共存场景中。
在评估共存性能方面，目前还没有文献考虑捕获效应。因此，本文首先研究了共存场景下的捕获效应问题，提出了捕获模型，然后推导出捕获概率。基于推导出的捕获概率，将LAA接入方案建模为具有捕获效应的新的2维马尔可夫模型，其中退避计数器的减少不仅取决于空闲时隙，还取决于捕获效应发生的时隙。最后，大量的仿真和数值结果验证了所提出的马尔可夫模型和捕获模型的有效性。
一些研究人员深入研究了LAA和WiFi网络的共存性能。然而，在实际共存场景中，他们没有考虑可能的捕获效应。文献[4]考虑到扩展空闲信道接入(Extended CCA, ECCA)期间的不完美频谱感知，将LAA-LBT建模为2维离散时间马尔可夫链。文献[7]研究了LAA和WiFi共存系统中LAA Cat 4 LBT过程的建模。文献[8]推导出两种最优传输策略，ORLA和OLAA，大大提高了LAA的吞吐量。文献[9]为与WiFi站点共存于单一免授权信道上的LAA站点设计了一种最佳通信策略。文献[10-12]使用随机几何理论对LTE LAA方案进行建模，并推导出其性能表达式。文献[13]提出了一种新的2维马尔可夫链模型。文献[14]考虑了与不对称的隐藏的WiFi接入点(Access Points, APs)共存的LAA小基站(Small Base Station, SBS)，从理论上推导出稳态概率、吞吐量和信道接入延迟的表达式。
一些研究人员考虑了无线局域网(Wireless Local Area Networks, WLANs)中的捕获效应。文献[15]开发了一个分析模型来计算WLAN中无捕获效应和有捕获效应时AP的饱和吞吐量。文献[16]研究了考虑捕获效应和定向天线的有损无线环境中WLAN的吞吐量性能。文献[17]提出了非饱和流量条件下IEEE 802.11协议在数据链路层中的吞吐量分析。文献[18]采用了直接序列扩频技术来分析IEEE 802.11协议下的捕获效应。另外，文献[19]在评估自动上行帧(Autonomous Uplink Future Enhanced LAA, AUL FeLAA)(不需要基站调度允许)与WiFi的共存性能时考虑到了捕获效应。
从以上讨论可知，LAA-WiFi共存系统的性能已经得到了广泛的研究[7,9,12-14,20]。文献[15-19]研究了捕获效应对基于IEEE 802.11 分布式控制功能协议的WLAN性能的影响。事实上，LAA网络和WLAN之间有很大的区别，可以概括如下：(1)一个LAA网络中只有一个信道竞争者(即SBSs)，这个竞争者调度获得的信道机会为它的用户服务。相反，一个WiFi网络中可能有许多信道竞争对手，其中包括WiFi AP和它的用户。每个竞争设备获得的信道完全由自己使用。因此，在一个LAA-WiFi网络中，LAA SBS与其他SBS, WiFi APs及其WiFi用户竞争信道。此外，在共存场景中，捕获效应不仅来自不同的LAA下行链路传输之间的碰撞，还来自LAA下行链路传输与WiFi APs或其用户之间的碰撞；(2)实际共存场景中，信道竞争对手(如SBS、APs及其用户)的分布比在一个WLAN中的更密集；(3)因为流量非常大，LAA SBSs可能总是有数据要传输，而APs及其用户可能并不处于很繁忙的流量中(APs可能有，但其站点可能没有)。因此，LAA-WiFi共存网络中的捕获效应不同于WiFi网络中的捕获效应，其对网络性能的影响也不同。而且，文献[15-17,21]提出的马尔可夫模型并未与捕获效应结合，因而没有考虑到捕获效应对传输概率的影响，进而可能导致性能评估的较大偏差。文献[19]虽然考虑到共存场景中的捕获效应。然而，这篇文献考虑的是捕获效应对流量未饱和时AUL FeLAA-WiFi共存性能的影响。
目前还没有文献考虑到捕获效应对LAA-WiFi共存系统的影响，如果不考虑LAA-WiFi共存网络中可能的捕获效应，那么评估的共存性能可能与实际情况产生较大的偏差。因此，本文在LAA-WiFi共存网络中考虑到了可能的捕获效应，并深入研究其对共存性能的影响。
2. 共存模型
如图1所示，属于不同运营商的
nl 个SBSs与其附近的nw 个WiFi设备(即WiFi APs及其服务的用户)工作在同一免授权频段。本文中LAA仅考虑用于补充下行链路传输，WiFi设备可用于上行链路和下行链路传输。考虑到LAA仅在授权频谱不能满足LTE用户的需求时采用，因此假设共存场景中的流量是饱和的，即LAA SBSs总是有数据要传输。在WiFi和LAA共存场景中，考虑到信号传输距离产生的衰减和瑞利衰落对无线传播建模的影响，接收功率
Pr 可以计算为Pr=K2(4πλ)2d−ηPt (1) 其中，
Pt 为传输功率，d 为信号传输距离，λ 为信号波长，η 为路径损耗指数(在没有直接信号路径的情况下通常大于3.5[18])。此外，我们假设所有信道都受瑞利衰落约束，其中衰落变量K 以参数α 指数分布[12]。3. 模型分析
3.1 捕获模型
通常认为当两个信号在相同信道上同时传输时，由于传输冲突，它们无法被接收。但在实际的通信中，如果一个信号与对其造成干扰的其他信号的功率差值大于一定的阈值，则该信号可以完成传输。这种现象被称为捕获效应[15-19]。由于LAA SBSs采用了集中调度机制，在一个SBS下的LAA用户之间没有信道竞争问题。因此，在共存场景中，本文主要研究SBSs之间、SBSs与WiFiAPs以及SBSs与WiFi用户之间的信道竞争所引起的捕获效应。
假设
Ps 表示在接收端成功接收的信号的功率，Pk 表示在同一信道上工作的干扰信号k 的功率，以下式基于捕获效应的定义始终成立Psi∑k=1Pk≥Cap_th (2) 其中，
Cap_th 是预定义的捕获阈值，i 是干扰源的数量。让Pf 表示在相同信道上传输的干扰信号中最强信号的功率，于是Pf≥Pk ，其中k∈{1,2,⋯,i} ，因此有Psi∑k=1Pk≥ PsiPf (3) 此外，捕获条件式(2)可以进一步表示为
PsiPf≥Cap_th (4) 假设发射功率相同，将式(1)代入式(4)可以得到
ds≤2η√KsKfdfη√(iCap_th) (5) 其中，
Ks 是信号成功传输的衰落变量，Kf 是功率最强的干扰信号的衰落变量，ds 为成功接收的信号的传输距离，df 为干扰信号的传输距离(即干扰发射机和接收机之间的交叉距离，也称为干扰距离)。在实际通信环境中，当一个信号与干扰信号之间的功率差大于某个阈值时，该信号仍然可以完成传输。为了分析捕获效应，基于考虑的共存场景，本文提出了LAA与WiFi共存下的捕获模型，如图2所示。其中，
SBSn 表示LAA小基站，UEl 表示从SBS接收数据的一个LAA其他户，它们之间的传输距离用rs 表示。其中，还可能存在一些在免授权信道上同时隙内传输数据的干扰源，比如其他的LAA SBS、用于下行链路传输的WiFi APs或者用于上行链路传输的WiFi用户。根据捕获效应的定义和式(5)，接收机UEl 能否捕获信道并成功接收SBSn 的数据主要取决干扰源与UEl 之间的距离，该距离用rf 表示。根据式(5)可知，当捕获效应发生时，干扰距离rf 需要满足条件rf≥12η√KsKfη√(iCap_th)⋅rs (6) 假设在共存场景中，LAA SBSs, WiFi APs及其用户设备是随机分布的。那么
UEl 能够成功接收来自SBSn 的数据的概率等于干扰源在场景的最小干扰距离和覆盖半径之间的环形区域中的概率可以计算为h(rs)=1−(η√(iCap_th)⋅rs2η√KsKfR)2 (7) 其中，R表示所考虑场景的覆盖半径。
同时，发射端和接收端
UEl 之间的距离的概率密度函数可以表示为f(rn)=2rnR2 (8) 根据条件
rf≤R 和式(5)可以推出rs≤2η√KsKfRη√(iCap_th) (9) 因此，在共存场景下的捕获概率可以表示为
P(cap,i)=∫2η√KsKfRη√iCap_th02rsR2⋅hi(rs)drs (10) 假设共存场景中有
M 个竞争节点，其中包括LAA SBS, WiFi AP及其WiFi用户，即M=nl+nw 。则i 个干扰节点在同一时隙时间内同时传输数据的概率可以计算为Pi=Ci+1Mτ(i+1−j)lτjw(1−τl)(nl−(i+1−j))(1−τw)nw−j (11) 其中，
τl 和τw 分别表示在LAA和WiFi网络中任一时隙时间内的传输概率，j 表示在i+1 节点中WiFi APs和WiFi用户的数量。最后，通过联立式(10)和式(11)可以获得捕获概率
pcap pcap=M−1∑i=1PiP(cap,i) (12) 3.2 2维离散时间马尔可夫模型
现有文献一般认为传输冲突必然会导致数据重传，然后进入下一退避阶段。然而，在实际场景中，当一个信号和其他信号之间的接收功率之差超过某个阈值时，仍然可以成功接收该信号。特别是在由异构网络组成的共存场景中，由于传输冲突更多，捕获效应可能更加频繁地发生。因此，即使发生传输碰撞，成功接收数据的接收端仍然可能向其发射端发送ACK反馈。然而，设备不会进入下一个退避阶段。
根据捕获效应的定义和特征，捕获效应仅可能发生在传输碰撞中，捕获概率是传输碰撞概率的子集。假设在每个数据包传输中都以一个独立且恒定的概率pcol发生碰撞，且与重传次数无关。当发生传输碰撞时，基于上述捕获效应的分析，来自LAA SBS的数据仍然可能被它们的用户成功接收，然后将ACK反馈发送到SBS。当SBS接收到ACK反馈时，它将直接进入扩展空闲信道检测(Extended Clear Channel Assessment, ECCA)的初始退避阶段，并准备发送新的数据包。因此，导致LAA SBS进入下一退避阶段的传输碰撞的实际概率是原始碰撞概率的子集，可以被计算为
pl=pcol(1−pcap) (13) 考虑到捕获效应和LAA接入方案的特点，能够将具有捕获效应的LAA方案(Cat 4)建模为2维离散马尔可夫模型，如图3所示。在所提出的模型中，计数器的减少不仅取决于信道上空闲的时隙，还取决于数据包碰撞期间由于捕获效应而能够成功接收的时隙。
令
s(t) 表示退避阶段的随机过程，b(t) 表示t 时刻退避时间计数器的随机过程，其中t 表示离散整数时间刻度。时间刻度t 对应于时隙的开始，退避计数器在每个时隙的结尾处减小。为了便于描述，2维离散马尔可夫过程的状态转移概率可以简化为P{L1,k1|L0,k0}=P{s(t+1)=L1b(t+1)=k1|s(t)=L0,b(t)=k0} (14) 因此，马尔可夫链的状态转移概率能够被写为
P{L,k|L,k+1}=1,L∈[0,h],k∈[0,WL−2]P{I,n|I,n+1}=1−pl,n∈[0,N−2]P{0,k|I,0}=1W0,k∈[0,W0−1]P{L,k|L−1,0}=plWL,L∈[0,h],k∈[0,WL−1]P{h,k|m,0}=plWm,L∈[0,h],k∈[0,Wm−1]P{0,k|L,0}=1−plW0,L∈[0,h],k∈[0,WL−1]P{0,k|I,n}=plW0,n∈(0,N−1],k∈[0,W0−1]P{I,N−1|h,0}=pl}→ (15) 假设
Wm 表示最大退避竞争窗口(Contention Window, CW)值，初始空闲信道检测(Initial Clear Channel Assessment, ICCA)退避阶段和ECCA退避阶段分别用I和L表示。注意，当重传时间大于最大退避阶段时，CW值不再增加。此外，当数据包的重传次数达到预定的阈值时，丢弃该数据。马尔可夫方程式(15)的解释如下所述：第1个等式表明，当在ECCA过程中检测到信道空闲时，退避计数器数值减小，否则，将会冻结退避计数器的数值；第2个等式表明，当在ICCA过程中检测到信道空闲时，退避计数器数值减小；第3个等式表明，如果在ICCA期间检测到的空闲时隙数未达到预定的值或LAA SBS准备发送连续数据包，则SBS将进入ECCA过程并自动执行随机退避过程；第4个等式表明LAA SBS进入下一个阶段；第5个等式表明，在达到最大退避CW之后，CW不会随着重传次数的增加而增加；第6个等式表明，如果前一个数据包已经被成功传输，则SBS将进入初始退避阶段并准备好传输下一个数据包；第7个等式表明，如果在ICCA期间检测到信道处于繁忙状态，SBS立即进入ECCA过程；第8个等式表明，如果在指定的最大冲突/重传次数内未能成功发送数据包，则该数据包将被丢弃，并且发送端再次开始执行新的ICCA过程。假设
bL,k=limt→∞P{s(t)=L,b(t)=k},L∈(0,h),k∈(0,WL−1) 为马尔可夫链的平稳分布，不难得到马尔可夫链的封闭表达式。首先，根据马尔可夫链可以得到bI,n=(1−pl)N−1−nbI,N−1,n∈[0,N−1] (16) bL,0=bL−1,0×pl→bL,0=b0,0×pLl,L∈[0,h] (17) 然后联立上述表达式后可以得到
bL,k=WL−kWLpLlb0,0,L∈[0,h] (18) h∑L=0bL,0=1−ph+1l1−plb0,0 (19) 通过图3中的马尔可夫链模型可以获得
b0,0=bI,N−1(plW0+plW0+⋯+plW0⏟W0)+bI,N−2(plW0+plW0+⋯+plW0⏟W0)+⋯+bI,0(plW0+plW0+⋯+plW0⏟W0)+bI,0(1−pl)=1−(1−pl)NplplbI,N−1+(1−pl)N−1⋅bI,N−1(1−pl)=[1−(1−pl)N−1+(1−pl)N−1]bI,N−1=bI,N−1 (20) 因此，信道接入过程和碰撞概率之间的关系最终可以通过归一化条件确定，其可以表示为
1=N−1∑n=0bI,n+h∑L=0WL−k∑k=0bL,k=1−(1−pl)NplbI,N−1+h∑L=0WL−k∑k=0WL−kWLpLlb0,0=1−(1−pl)Nplb0,0+(h∑L=0pLl+m∑L=0pLlWL+h∑m+1pLlWL)b0,02=1−(1−pl)Nplb0,0+[1−ph+1l1−pl+1−(2pl)m+11−2plW0+2mpm+1l(1−ph−ml)1−plW0]b0,02 (21) 根据方程式(20)和方程式(21)能够得到
b0,0=2pl(1−pl)(1−2pl)pl(1−2pl)(1−ph+1l)+W0pl(1−pl)[1−(2pl)m+1]+(1−2pl)[2mW0pm+2l(1−ph−ml)+2(1−pl)(1−(1−pl)N)] (22) 通过联立表达式(18)，式(19)与式(22)从而可以得到捕获效应下的传输概率，其可以表示为
τl=bI,0+h∑L=0bL,0=(1−pl)N−1b0,0+h∑l=0pLlb0,0=[(1−pl)N+(1−ph+1l)1−pl]b0,0=2pl(1−2pl)[(1−pl)N+(1−ph+1l)]pl(1−2pl)(1−ph+1l)+W0pl(1−pl)[1−(2pl)m+1]+(1−2pl)[2mW0plm+2(1−ph−ml)+2(1−pl)(1−(1−pl)N)] (23) 3.3 碰撞概率分析
LAA网络中的传输碰撞可能发生在不同的LAA SBSs之间或者SBS和WiFi设备(即WiFi APs及其服务的用户)之间。因此，LAA碰撞概率等于剩余
nw 个WiFi设备和nl−1 个SBSs中存在至少一个SBS或WiFi设备在同一时隙内传输数据的概率，其可以表示为[21-23]pl=1−(1−τl)nl−1(1−τw)nw (24) 相似地，WiFi的碰撞概率
pw 能够表示为pw=1−(1−τw)nw−1(1−τl)nl (25) 通过联立表达式(12)、式(13)、式(24)和式(25)，从而可以得到等式(26)，其能够通过数值方法例如MATLAB中的fslove函数而被求解。
F(τl,τw,Pcap,pl,pw)={τlτwpcap=M−1∑i=1PiP(cap,i)pl=1−(1−τl)nl−1(1−τw)nwpw=1−(1−τw)nw−1(1−τl)nl (26) 3.4 吞吐量分析
让
pt,l 表示至少一个LAA SBS在任何时隙传输数据的概率，pt,w 表示至少一个WiFi设备(WiFi AP或者WiFi用户)在任何时隙内传输数据的概率，那么它们能够分别表示为pt,w=1−(1−τw)nw 和pt,l=1−(1−τl)nl 。那么， LAA SBSs的吞吐量Sl 和WiFi设备的吞吐量Sw 分别表示为[4,11,19,23]Sl=pt,lps,l(1−pt,w)TdlTs (27) Sw=pt,wps,w(1−pt,l)TdwTs (28) 其中，
ps,l 和ps,w 分别为在至少一个LAA SBS/WiFi设备传输数据的条件下，只有一个SBS/WiFi设备传输数据的概率，Tdl 和Tdw 分别表示LAA帧和WiFi数据包的持续时间。4. 性能评估
本文使用了网络模拟器(Network Simulator-3, NS-3)验证所提出模型的有效性。通过对NS-3原有的传播损耗模型源代码中进行一些修改，本文得到了瑞利衰落参数
α=1 、路径损耗指数η=4 、标准差为0的传播模型[21]。在仿真中，WiFi APs以及其WiFi用户均采用IEEE 802.11n DCF协议的NetDevice类，LAA方案的信道竞争过程采用LBT access manager模块。这些能够从网址http://code.nsnam.org/laa/ns-3-lbt 下载。最后，本文构建了一个共存场景，其中存在不同的竞争节点。此外，使用由两个20 MHz窄带未授权信道聚合而成的40 MHz信道，还使用了LAA B型双载波传输方案和WiFi多载波信道接入方案[24,25]。配置参数如表1所示。表 1 仿真参数参数 取值 参数 取值 参数 取值 参数 取值 MAC首部 192 bit 传播延时Tdef 1 μs DIFS/SIFS 34/16 μs 频率 5.15 GHz PHY首部 224 bit 最大重传次数h 15 ICCA持续时隙L 8时隙 传输功率 23 dBm ACK 112 bit 时隙大小σ 9 μs ECCA延迟长度Td 4时隙 覆盖半径R 50 m 数据包负载 8192 bit 免授权频段带宽 20 MHz LAA/WiFi数据速率 120 Mbit/s/70 Mbit/s 免授权频段的数量 2 4.1 碰撞概率比较
图4(a)显示具有捕获效应和不具有捕获效应时碰撞概率的比较(Cap_threshold = 3)。从图4(a)可以看出，碰撞概率随着WiFi设备的增加而增加。这是因为WiFi设备数量的增加将意味着更多的竞争节点(即WiFi APs及WiFi用户)参与竞争免授权信道，进而导致传输碰撞的增加。从图4(a)还可以看出，随着WiFi设备数量的增加，无论有没有捕获效应，在共存系统中碰撞概率都小于用WiFi设备代替SBSs的独立WiFi系统的碰撞概率。这是因为在LAA方案中设置了最大重传次数，而且，当重传次数达到最大预定值时，数据包将被丢弃，SBS将进入ICCA阶段进行新的数据传输。相反，根据Bianchi的模型[23]，在WiFi网络中，数据包能够一直重传直到传输成功，同时发送端直接进入退避过程进行新数据的传输。这证明了相比于WiFi设备，LAA SBSs可以带来更低的碰撞概率。从图4可以看出，捕获效应下的碰撞概率低于没有捕获效应时的碰撞概率。这是因为当传输碰撞发生时，最强的信号仍然可能被成功地接收。图4(b)和(c)显示Cat-3和Cat-4方案下的WiFi碰撞概率的比较(Cap_th = 3)。图4(b)显示当LAA SBSs的数量保持不变时，WiFi碰撞概率随着WiFi设备的增加而增加。图4(c)显示当WiFi设备的数量保持不变时，WiFi碰撞概率随着LAA SBSs的增加而增加。从图4(b)和(c)可以看出，当采用相同的接入方案时，具有捕获效应的WiFi碰撞概率总是小于无捕获效应的WiFi碰撞概率。这是因为在实际的通信环境中，并非所有的碰撞信号都传输失败，接收功率更高的碰撞信号仍然可能被成功捕获。同时Cat-3方案的碰撞概率更高于Cat-4方案，这是因为在Cat-3方案中采用固定退避CW，而Cat-4方案中采用了基于二进制指数退避的CW，后者能够有效地平滑流量负载，从而能够降低碰撞概率。
4.2 吞吐量比较
图5(a)显示独立的WiFi系统和共存系统下的总吞吐量的比较。从图5(a)可以看出，不管有无捕获效应，独立WiFi系统的吞吐量都小于LAA与WiFi共存系统的总吞吐量。这是因为在独立的WiFi系统中碰撞概率更大，导致吞吐量更小。从图5(a)还可以看出，考虑捕获效应时的吞吐量要高于不考虑捕获效应时的吞吐量。图5(b)显示Cat-3和Cat-4方案下总吞吐量的比较。从图5(b)可以看出，在Cat-3方案下的吞吐量总是大于Cat-4方案下的吞吐量。这是因为Cat-3方案在接入信道时采用的固定退避CW比Cat-4方案采用的二进制指数退避CW更具有侵略性。这将导致WiFi碰撞概率的增加，如图5(c)所示。当竞争节点的数量逐渐增多时，两种方案的总吞吐量相差越来越小。这是因为随着竞争设备数量的增加，两种方案下的碰撞概率都会变得越来越高，进而使得两种方案的吞吐量越来越接近。图5(c)显示Cat-3和Cat-4两种方案下WiFi和LAA吞吐量的比较。从图5(c)可以看出，在Cat-3方案下LAA和WiFi的差异明显大于在Cat-4方案下的差异。这是因为与Cat-4方案相比，基于固定CW的Cat-3在接入信道时更具有侵略性。这使得Cat-3方案下的LAA SBSs具有更多的传输机会，从而减少了WiFi设备的传输机会。图5(d)显示不同WiFi设备数量下的LAA和WiFi的吞吐量。从图5(d)可以看出，考虑捕获效应的LAA和WiFi的吞吐量总是大于不考虑捕获效应的LAA和WiFi的吞吐量。
4.3 捕获阈值对碰撞概率和吞吐量的影响
图6(a)和图6(b)显示捕获阈值对吞吐量的影响。从图6(a)和(b)可以看出， 总吞吐量、LAA和WiFi吞吐量随着捕获阈值的减小而增大。这是因为捕获阈值的降低意味着捕获效应发生条件的降低，增加了捕获效应发生的概率，进而增加了吞吐量。图6(c)显示了捕获阈值对碰撞概率的影响。图6(c)显示碰撞概率随着捕获阈值的降低而降低。
5. 结束语
考虑到LAA和WiFi实际共存场景下可能的捕获效应，本文对其共存性能进行了深入研究。首先，考虑捕获效应的定义，提出了共存场景下的捕获模型，并推导出捕获概率；然后，将LAA接入机制(Cat-3、Cat-4)建模为具有捕获效应的2维离散马尔可夫模型，其中退避计数器的减少不仅取决于空闲时隙，还取决于捕获效应发生的时隙。基于提出的具有捕获效应的马尔可夫模型，从理论上推导出LAA和WiFi的碰撞概率和吞吐量。大量的仿真和数值结果证明了所提出的模型的有效性。仿真结果显示捕获效应能够显著地降低碰撞概率，增加LAA和WiFi吞吐量。这也证明了考虑捕获效应的必要性。此外，仿真结果还显示捕获阈值对共存性能有重要影响。因此，为了准确地评估共存性能，需要根据实际信道情况设计最佳的捕获阈值。
-
DESHPANDE M D and STATON L. Determination of windspeed within a weather storm using airborne Doppler radar[C]. IEEE Proceedings of the Southeastcon’91, Williamsburg, USA, 1991: 508–519. WILSON J W and WAKIMOTO R M. The discovery of the downburst: T. T. Fujita’s contribution[J]. Bulletin of the American Meteorological Society, 2001, 82(1): 49–62. doi: 10.1175/1520-0477(2001)082<0049:TDOTDT>2.3.CO;2 韩雁飞, 刘夏, 李海, 等. 基于微物理特性的三维低空风切变雷达回波仿真[J]. 系统工程与电子技术, 2016, 38(2): 298–304. doi: 10.3969/j.issn.1001-506X.2016.02.10HAN Yanfei, LIU Xia, LI Hai, et al. Microphysics-based radar signal simulation for the three dimensional low altitude wind shear[J]. Systems Engineering and Electronics, 2016, 38(2): 298–304. doi: 10.3969/j.issn.1001-506X.2016.02.10 韩伟, 张道尚, 李智. 载机偏航对雷达目标检测性能的影响分析[J]. 雷达科学与技术, 2015, 13(2): 167–172. doi: 10.3969/j.issn.1672-2337.2015.02.012HAN Wei, ZHANG Daoshang, and LI Zhi. Influence of aircraft crabbing on target detection performance of AEW radar[J]. Radar Science and Technology, 2015, 13(2): 167–172. doi: 10.3969/j.issn.1672-2337.2015.02.012 白健, 李勇, 高霞, 等. 基于Prony模型的低空风切变快速检测算法[J]. 计算机测量与控制, 2009, 17(10): 1889–1891. doi: 10.16526/j.cnki.11-4762/tp.2009.10.001BAI Jian, LI Yong, GAO Xia, et al. Low-level wind shear detection algorithm based on Prony model[J]. Computer Measurement &Control, 2009, 17(10): 1889–1891. doi: 10.16526/j.cnki.11-4762/tp.2009.10.001 LI Hai, ZHOU Meng, GUO Qinghua, et al. Compressive sensing-based wind speed estimation for low-altitude wind-shear with airborne phased array radar[J]. Multidimensional Systems and Signal Processing, 2018, 29(2): 719–732. 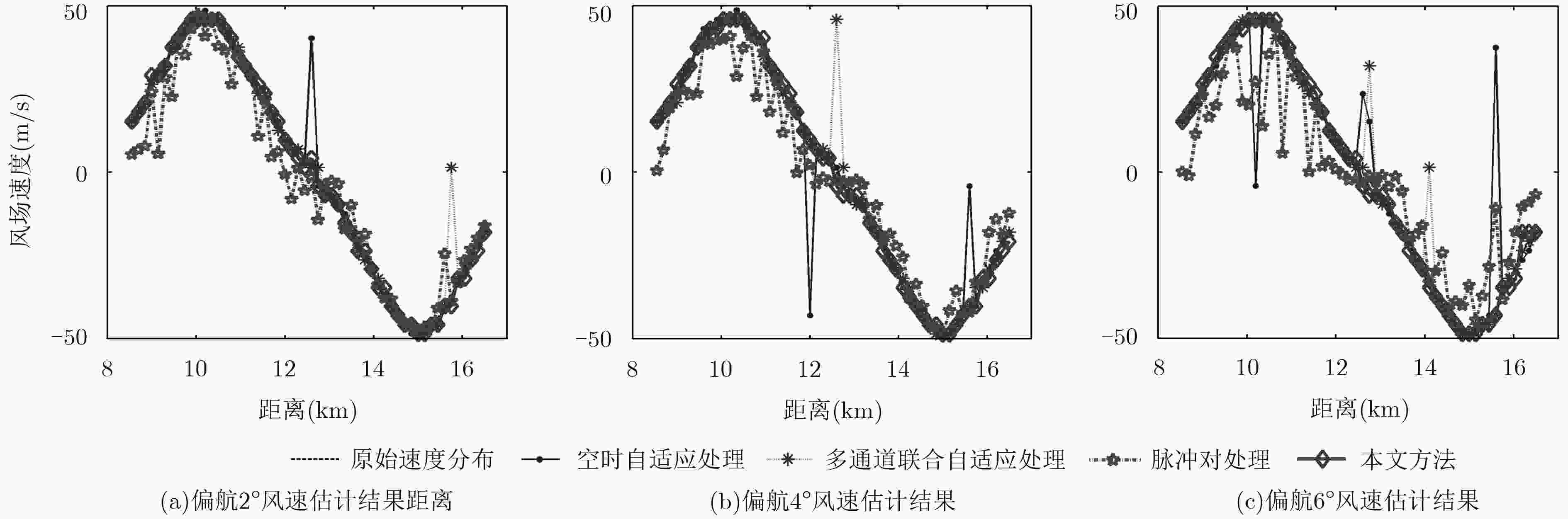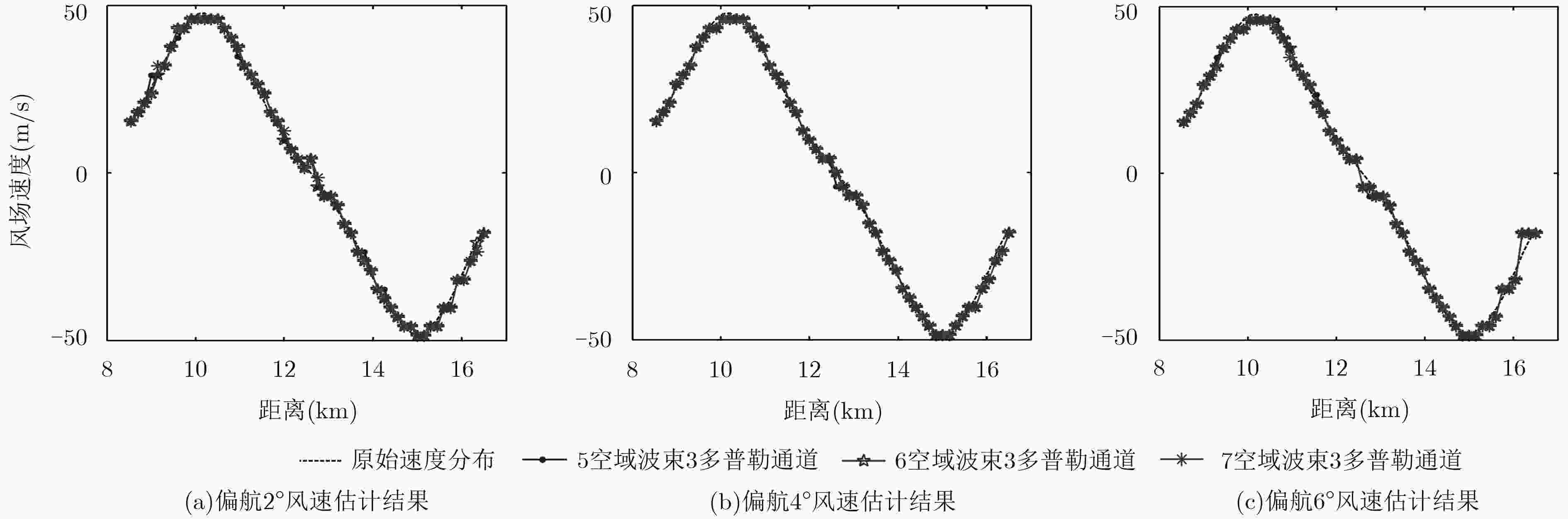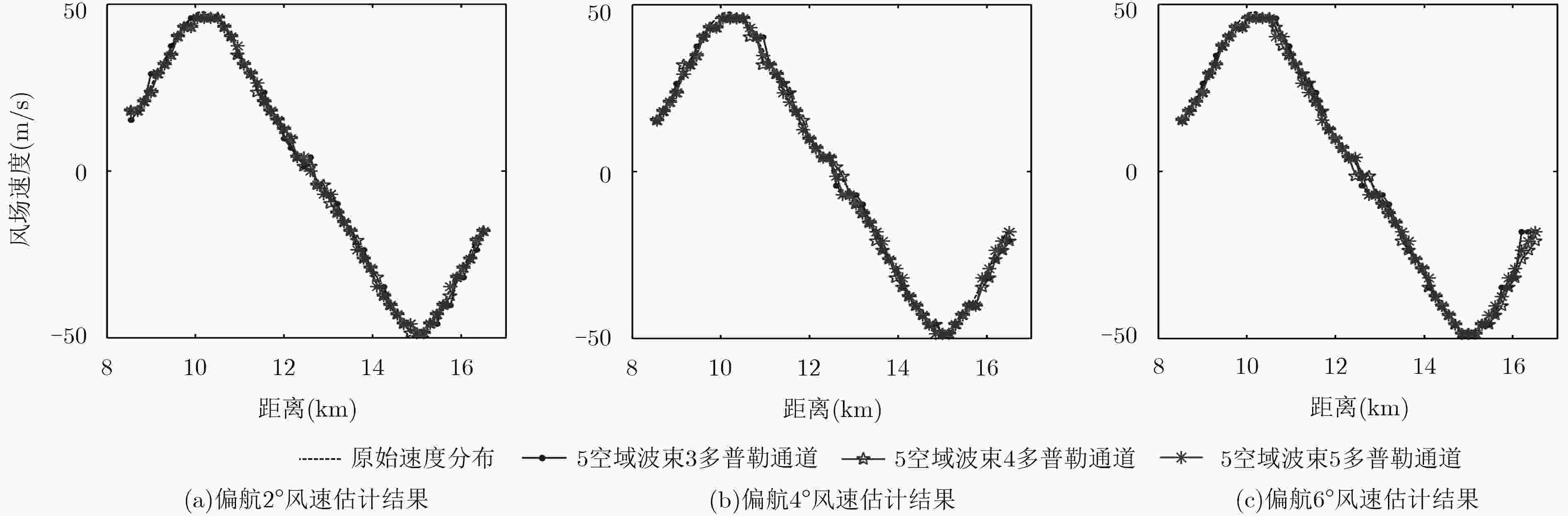doi: 10.1007/s11045-016-0448-6 吴仁彪, 张彪, 李海, 等. 基于空时自适应处理的低空风切变风速估计方法[J]. 电子与信息学报, 2015, 37(3): 631–636. doi: 10.11999/JEIT140697WU Renbiao, ZHANG Biao, LI Hai, et al. Wind speed estimation for low-attitude windshear based on space-time adaptive processing[J]. Journal of Electronics &Information Technology, 2015, 37(3): 631–636. doi: 10.11999/JEIT140697 LI Hai, ZHOU Meng, WU Renbiao, et al. Wind speed estimation of low-altitude wind-shear based on multiple Doppler channels joint adaptive processing[C]. Proceedings of 2016 IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 2016: 3116–3120. 李海, 周盟, 陈筱浅, 等. 基于多通道联合自适应处理的微下击暴流中心风速估计方法[J]. 电子与信息学报, 2017, 39(7): 1619–1625. doi: 10.11999/JEIT161094LI Hai, ZHOU Meng, CHEN Xiaoqian, et al. Multiple doppler channels joint adaptive processing based central wind speed estimation for microburst[J]. Journal of Electronics &Information Technology, 2017, 39(7): 1619–1625. doi: 10.11999/JEIT161094 KLEMM R. Principle of Space-time Adaptive Processing[M]. 3rd ed. London, UK: IET Publishers, 2006: 1–133. BOYER E, LARZABAL P, ADNET C, et al. Parametric spectral moments estimation for wind profiling radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(8): 1859–1868. doi: 10.1109/TGRS.2003.813487 姚晖. 分布式信号源参数估计技术研究[D]. [博士论文]. 解放军信息工程大学, 2013: 9–25.YAO Hui. Research on parameter estimation method for distributed sources[D]. [Ph.D. dissertation], PLA Information Engineering University, 2013: 9–25. 王娟, 王彤, 吴建新. 非正侧阵机载雷达杂波谱迭代自适应配准方法[J]. 系统工程与电子技术, 2017, 39(4): 742–747. doi: 10.3969/j.issn.1001-506X.2017.04.08WANG Juan, WANG Tong, and WU Jianxin. Registration-based compensation using iterative adaptive approach in non-side-looking airborne radar[J]. Systems Engineering and Electronics, 2017, 39(4): 742–747. doi: 10.3969/j.issn.1001-506X.2017.04.08 文珺, 廖桂生, 李明. 一种机载前视雷达杂波距离依赖性补偿方法[J]. 系统工程与电子技术, 2010, 32(6): 1187–1190. doi: 10.3969/j.issn.1001-506X.2010.06.017WEN Jun, LIAO Guisheng, and LI Ming. Method to compensate clutter range dependence for airborne forward looking radar[J]. Systems Engineering and Electronics, 2010, 32(6): 1187–1190. doi: 10.3969/j.issn.1001-506X.2010.06.017 期刊类型引用(4)
1. 姜迈，沙贵君，李宁. 基于PUCS与DTCWT的红外与弱可见光图像融合. 红外技术. 2022(07): 716-725 . 
百度学术2. 郭锋锋. 一种结合清晰区域增强多聚焦图像融合算法. 攀枝花学院学报. 2021(05): 90-95 . 百度学术3. 赵春晖，郭蕴霆. 一种快速的基于稀疏表示和非下采样轮廓波变换的图像融合算法. 电子与信息学报. 2016(07): 1773-1780 . 
本站查看4. 才华，陈广秋，刘广文，耿朕野，杨勇. 基于边界约束最优投影梯度NMF的TINST域图像融合方法. 吉林大学学报(理学版). 2016(05): 1087-1095 . 百度学术其他类型引用(4)
-
下载:
百度学术
计量
- 文章访问数: 1905
- HTML全文浏览量: 942
- PDF下载量: 55
- 被引次数: 8
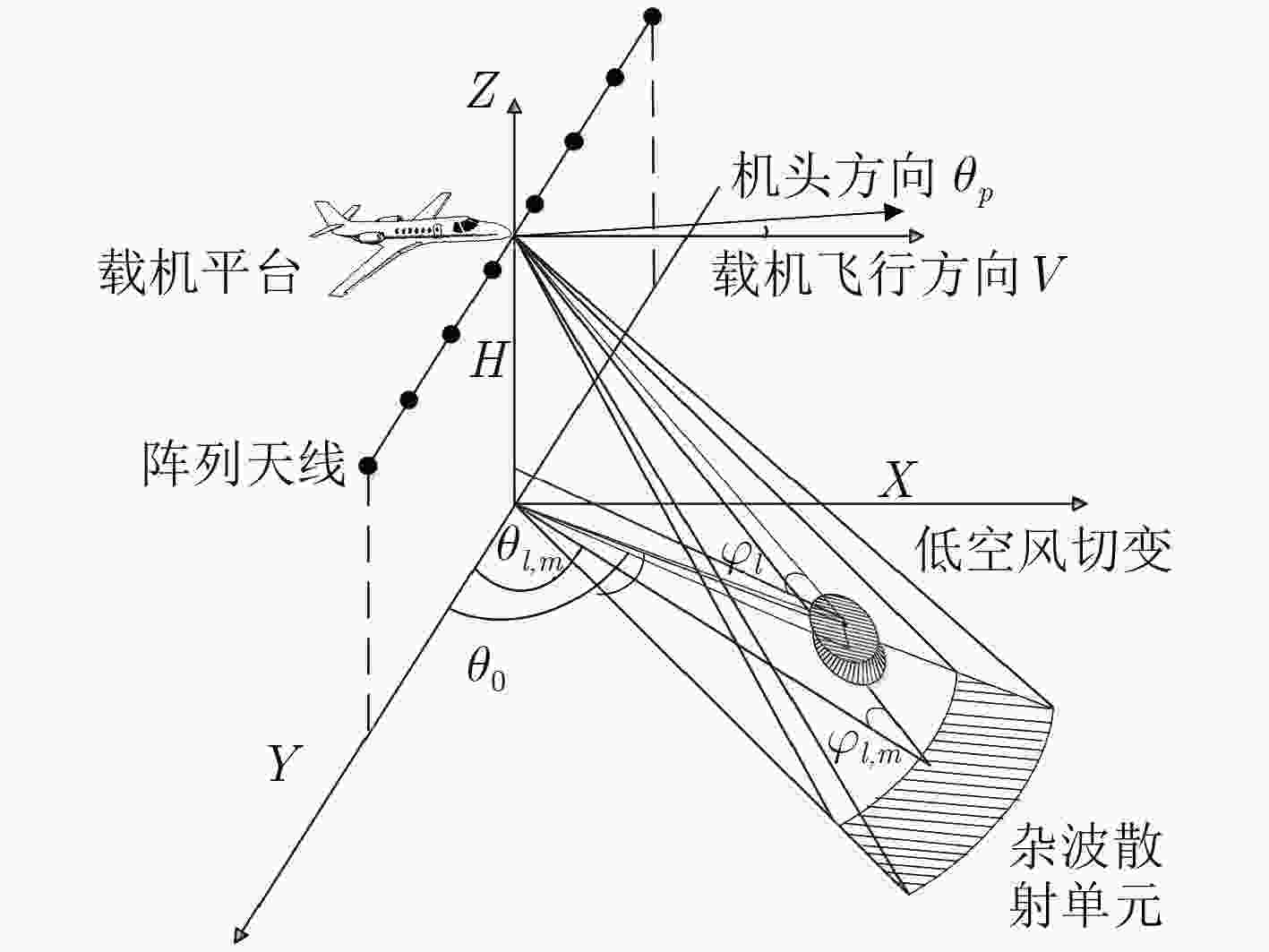
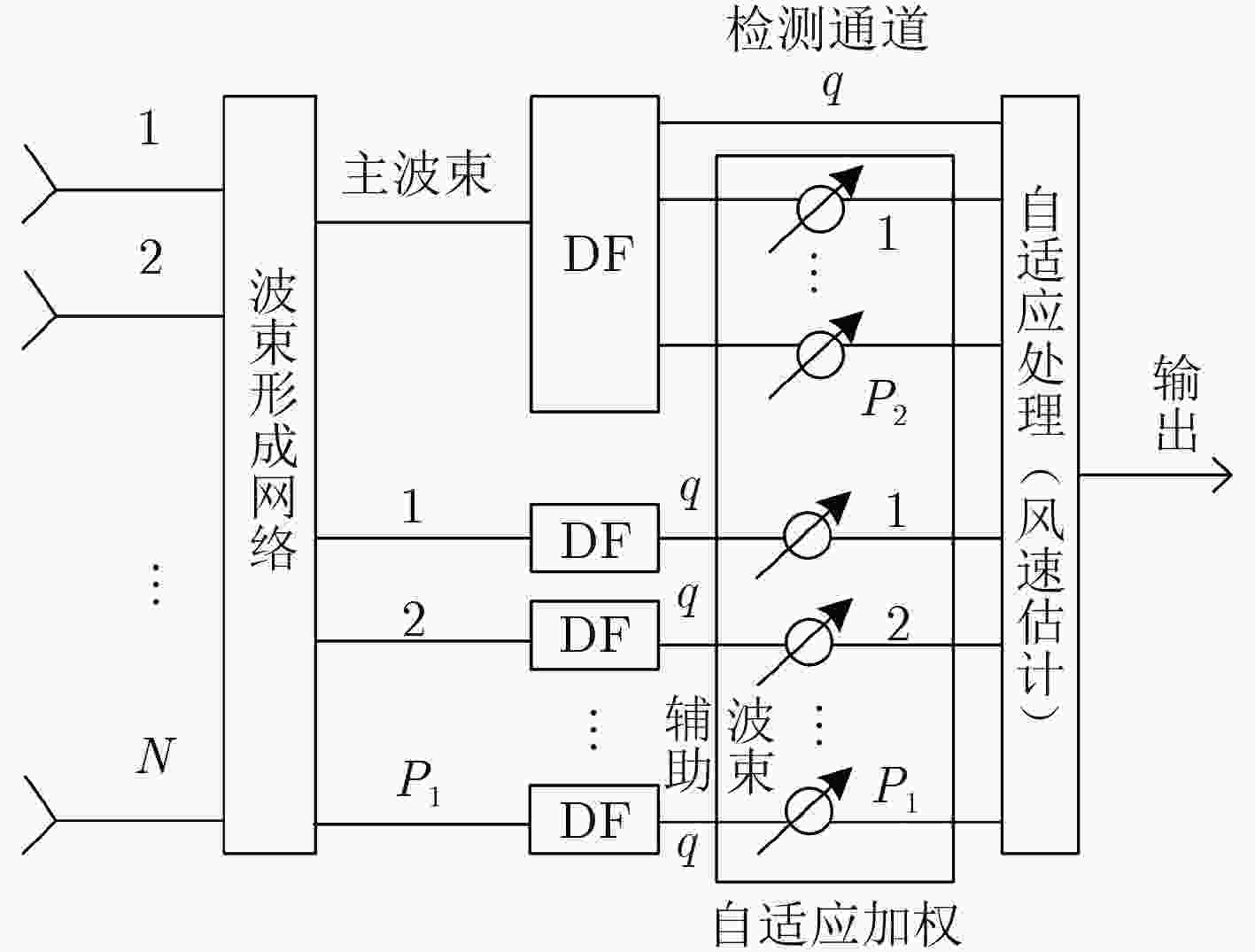
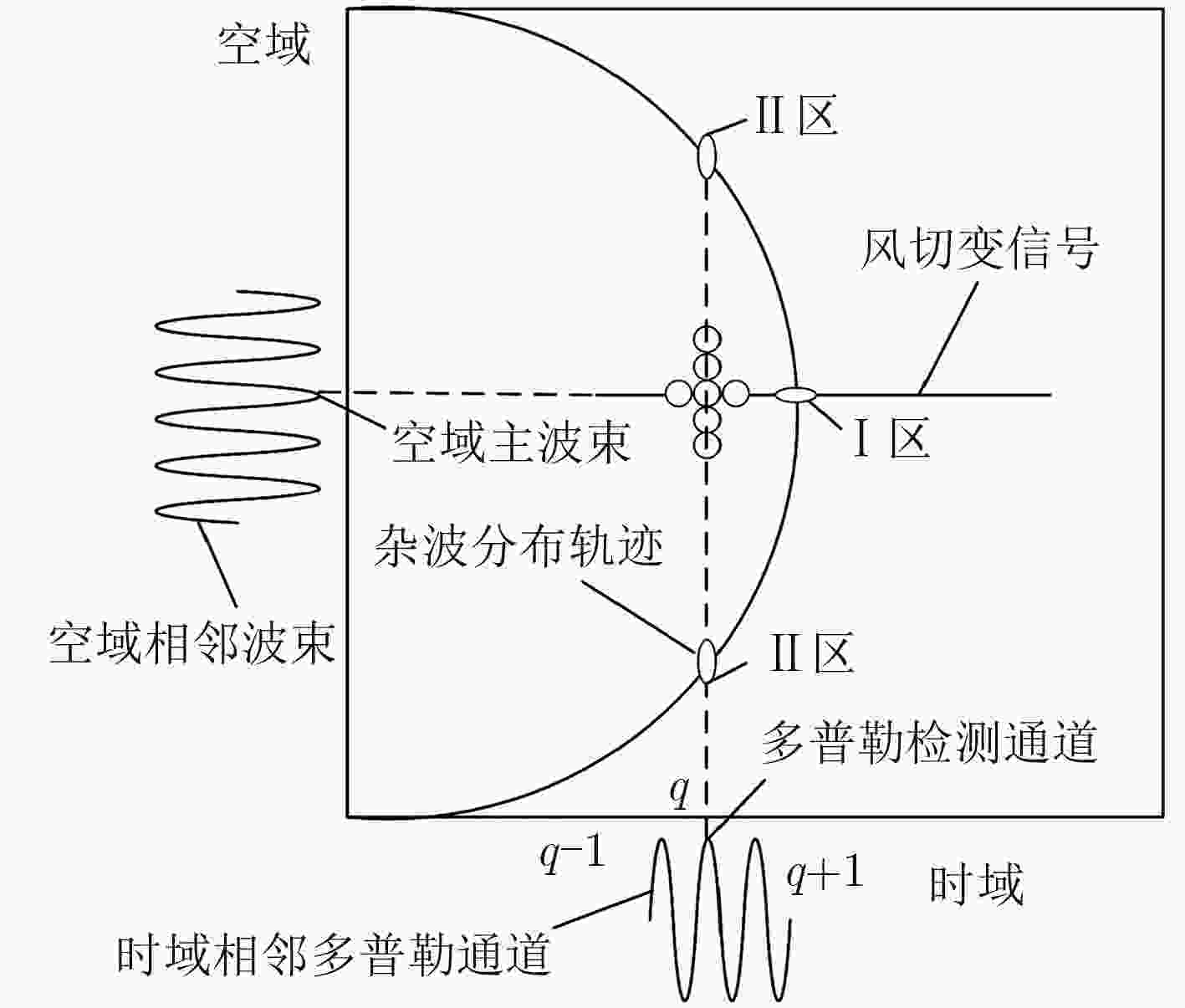
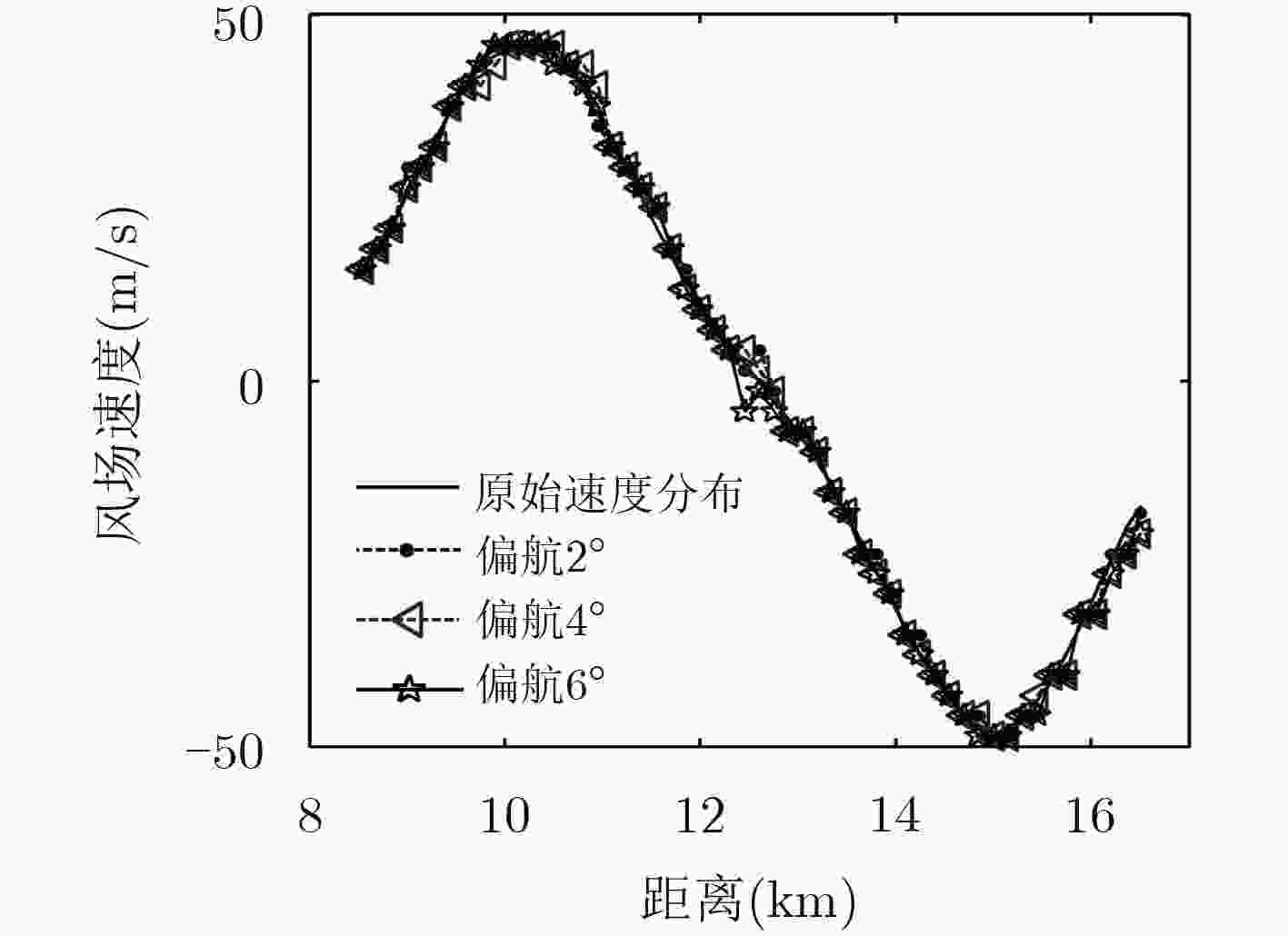
下载:
