Application of Improved Multiverse Algorithm to Large Scale Optimization Problems
-
摘要: 针对多元宇宙优化(MVO)算法中虫洞存在机制、白洞选择机制等不足,该文提出一种改进多元宇宙优化算法(IMVO)。设计固定概率的虫洞存在机制和前期快速收敛后期平缓收敛的虫洞旅行距离率,加快算法全局探索能力和快速迭代能力;提出黑洞的随机白洞选择机制,设计黑洞围绕白洞恒星进行公转并模型化,解决代间宇宙信息沟通的问题,中低维度数值比较实验验证了改进算法的优良性能。选取大规模实值问题较难优化的3个基准测试函数进行对比实验,改进算法在大规模优化问题上的求解精度和成功率方面具有较好的适用性和鲁棒性。Abstract: To overcome the mechanism shortcomings of wormhole and white hole selection in the Multi-Verse Optimizer (MVO), an Improved Multi-Universes Optimization (IMVO) algorithm is proposed. To speed up global exploration ability and quick iteration ability, this thesis designs the existence mechanism of wormhole with fixed probability and the Travel Distance Rate (TDR) that its convergence from early stage's smoothly to later stage's fast. The random white hole selection mechanism is proposed; Black holes can revolve around selected white hole stars and is modelled to solve the problem of information communication of the Inter-generational Universes. The performance of IMVO is verified by comparison experiments in low-middle dimensions. Three benchmarks test functions are selected for comparison in large scale which are difficult to be optimized, the experimental results show that IMVO has good applicability and robustness with higher solving accuracy and success rate in large scale optimization problem.
-
表 1 文献[10]的时间复杂度
操作 计算复杂度 循环次数 初始化 O(N) 1×D 计算宇宙膨胀率 O(N) L×D 排序/标准化宇宙 O(N) L×D 黑白洞换维度 O(K) L×D 穿越选择 O((1–K)WEP) L×D 参数更新 O(1) L 表 2 本文的时间复杂度
操作 计算复杂度 循环次数 初始化 O(N) 1×D 计算宇宙膨胀率 O(N) L×D 黑白洞选择 O(N) L×D 策略1:穿越 O(N/2) L×D 策略2:公转 O(N/2) L×D 参数更新 O(1) L 表 3 单峰基准测试函数的50维对比实验
表 4 多峰基准测试函数的50维对比实验
表 5 基准测试函数30维度的算法对比实验
f1 f2 f5 f7 f9 f10 f11 f12 文献[6] 均值 6.54e-125 2.15e-73 27.27950 2.42e04 0 3.02e-15 0 0.087646 标准差 6.80e-125 3.64e-73 0.215438 4.41e-04 0 1.95e-15 0 0.011997 本文 均值 5.24e-21 1.86e-11 2.46e-20 3.41e-04 0 5.51e-12 0 1.14e-23 标准差 1.96e-20 1.37e-11 4.03e-20 3.23e-04 0 6.56e-12 0 1.90e-23 表 6 基准测试函数10维度的算法对比实验
函数 算法 DA[18] CSA[17] MVO[10] IMVO[11] 本文 f10 均值 2.28 1.07 8.06e-02 4.27e-05 9.66e-12 标准差 1.13 0.921 2.04e-01 2.22e-05 8.08e-12 最差值 4.20 3.02 1.16 1.04e-04 7.76e-11 最好值 4.44e-15 1.75e-03 1.17e-02 7.08e-06 3.67e-13 f12 均值 9.78e-01 3.83e-01 1.07e-02 1.25e-10 4.32e-23 标准差 8.58e-01 6.07e-01 5.70e-02 1.18e-10 1.06e-22 最差值 3.49 3.20 3.12e-01 4.45e-10 4.71e-22 最好值 4.84e-03 5.67e-05 9.21e-05 7.76e-12 9.15e-27 F 对比算法 D=200 D=500 均值 标准差 成功率(%) 均值 标准差 成功率(%) f2 文献[10] 7.50e-51 9.40e-51 100 1.10e-49 2.10e-49 100 文献[6] 1.60e-67 1.90e-67 100 5.30e-66 9.60e-66 100 本文 1.59e-10 1.43e-10 100 2.56e-10 2.41e-10 100 f5 文献[10] 1.98e+02 2.22e-01 0 4.96e02 4.66e-01 0 文献[6] 1.98e+02 5.43e-02 0 4.96e02 3.78e-01 0 本文 6.13e-20 1.29e-19 100 3.48e-19 4.15e-19 100 f10 文献[10] 5.15e-15 1.94e-15 100 5.86e-15 2.97e-15 100 文献[6] 8.88e-16 0 100 4.44e-15 0 100 本文 7.16e-12 6.87e-12 100 6.49e-12 1.13e-11 100 f12 文献[10] 8.09e-02 4.05e-02 0 9.19e-02 5.92e-02 0 文献[6] 2.02e-02 2.75e-02 0 8.30e-02 3.17e-02 0 本文 5.09e-24 8.06e-24 100 4.25e-24 9.01e-24 100 表 8 求解不同规模f2和f10函数的优化均值对比
表 9 改进算法的大规模实值优化结果(阈值为1)
F 对比算法 D=1000 D=2000 均值 标准差 成功率(%) 均值 标准差 成功率(%) f5 文献[10] 8.70e+08 7.81e+07 0 7.11e+09 3.23e+08 0 本文 2.05e-19 3.42e-19 100 5.62e-19 1.37e-18 100 f7 文献[10] 1.08e+04 8.35e+02 0 1.81e+05 9.44e+03 0 本文 2.52e-04 3.99e-04 100 2.70e-04 3.87e-04 100 f9 文献[10] 1.37e+04 3.36e+02 0 3.04e+04 3.28e+02 0 本文 0 0 100 0 0 100 -
MAHDAVI S, RAHNAMAYAN S, and SHIRI M E. Multilevel framework for large-scale global optimization[J]. Soft Computing, 2017, 21(14): 4111–4140. doi: 10.1007/s00500-016-2060-y BOLUFÉ-RÖHLER A, FIOL-GONZÁLEZ S, and CHEN S. A minimum population search hybrid for large scale global optimization[C]. Proceedings of 2015 IEEE Congress on Evolutionary Computation, Sendai, Japan, 2015: 1958–1965. doi: 10.1109/CEC.2015.7257125. 梁静, 刘睿, 于坤杰, 等. 求解大规模问题协同进化动态粒子群优化算法[J]. 软件学报, 2018, 29(9): 2595–2605. doi: 10.13328/j.cnki.jos.005398LIANG Jing, LIU Rui, YU Kunjie, et al. Dynamic multi-swarm particle swarm optimization with cooperative coevolution for large scale global optimization[J]. Journal of Software, 2018, 29(9): 2595–2605. doi: 10.13328/j.cnki.jos.005398 罗家祥, 倪晓晔, 胡跃明. 融合多种搜索策略的差分进化大规模优化算法[J]. 华南理工大学学报: 自然科学版, 2017, 45(3): 97–103. doi: 10.3969/j.issn.1000-565X.2017.03.014LUO Jiaxiang, NI Xiaoye, and HU Yueming. A hybrid differential evolution algorithm with multiple search strategies for large-scale optimization[J]. Journal of South China University of Technology:Natural Science Edition, 2017, 45(3): 97–103. doi: 10.3969/j.issn.1000-565X.2017.03.014 MIRJALILI S and LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51–67. doi: 10.1016/j.advengsoft.2016.01.008 龙文, 蔡绍洪, 焦建军, 等. 求解大规模优化问题的改进鲸鱼优化算法[J]. 系统工程理论与实践, 2017, 37(11): 2983–2994. doi: 10.12011/1000-6788(2017)11-2983-12LONG Wen, CAI Shaohong, JIAO Jianjun, et al. Improved whale optimization algorithm for large scale optimization problems[J]. Systems Engineering-Theory &Practice, 2017, 37(11): 2983–2994. doi: 10.12011/1000-6788(2017)11-2983-12 MIRJALILI S, MIRJALILI S M, and LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007 姜天华. 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控制与决策, 2018, 33(3): 503–508. doi: 10.13195/j.kzyjc.2017.0124JIANG Tianhua. Flexible job shop scheduling problem with hybrid grey wolf optimization algorithm[J]. Control and Decision, 2018, 33(3): 503–508. doi: 10.13195/j.kzyjc.2017.0124 梁静, 刘睿, 瞿博阳, 等. 进化算法在大规模优化问题中的应用综述[J]. 郑州大学学报: 工学版, 2018, 39(3): 15–21. doi: 10.13705/j.issn.1671-6833.2017.06.016LIANG Jing, LIU Rui, QU Boyang, et al. A survey of evolutionary algorithms for large scale optimization problem[J]. Journal of Zhengzhou University:Engineering Science, 2018, 39(3): 15–21. doi: 10.13705/j.issn.1671-6833.2017.06.016 MIRJALILI S, MIRJALILI S M, and HATAMLOU A. Multi-verse optimizer: A nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27(2): 495–513. doi: 10.1007/s00521-015-1870-7 赵世杰, 高雷阜, 徒君, 等. 耦合横纵向个体更新策略的改进MVO算法[J]. 控制与决策, 2018, 33(8): 1422–1428. doi: 10.13195/j.kzyjc.2017.0441ZHAO Shijie, GAO Leifu, TU Jun, et al. Improved multi verse optimizer coupling horizontal-and-vertical individual updated strategies[J]. Control and Decision, 2018, 33(8): 1422–1428. doi: 10.13195/j.kzyjc.2017.0441 CHOPRA N and SHARMA J. Multi-objective optimum load dispatch using Multi-verse optimization[C]. Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems, Delhi, India, 2016: 1–5. HU Cong, LI Zhi, ZHOU Tian, et al. A multi-verse optimizer with levy flights for numerical optimization and its application in test scheduling for network-on-chip[J]. PLOS One, 2016, 11(12): e0167341. doi: 10.1371/journal.pone.0167341 FARIS H, ALJARAH I, and MIRJALILI S. Training feedforward neural networks using multi-verse optimizer for binary classification problems[J]. Applied Intelligence, 2016, 45(2): 322–332. doi: 10.1007/s10489-016-0767-1 JANGIR P, PARMAR S A, TRIVEDI I N, et al. A novel hybrid particle swarm optimizer with multi verse optimizer for global numerical optimization and optimal reactive power dispatch problem[J]. Engineering Science and Technology, An International Journal, 2017, 20(2): 570–586. doi: 10.1016/j.jestch.2016.10.007 ALI E E, EL-HAMEED M A, EL-FERGANY A A, et al. Parameter extraction of photovoltaic generating units using multi-verse optimizer[J]. Sustainable Energy Technologies and Assessments, 2016, 17: 68–76. doi: 10.1016/j.seta.2016.08.004 MIRJALILI S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems[J]. Neural Computing and Applications, 2016, 27(4): 1053–1073. doi: 10.1007/s00521-015-1920-1 ASKARZADEH A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm[J]. Computers & Structures, 2016, 169: 1–12. doi: 10.1016/j.compstruc.2016.03.001 -





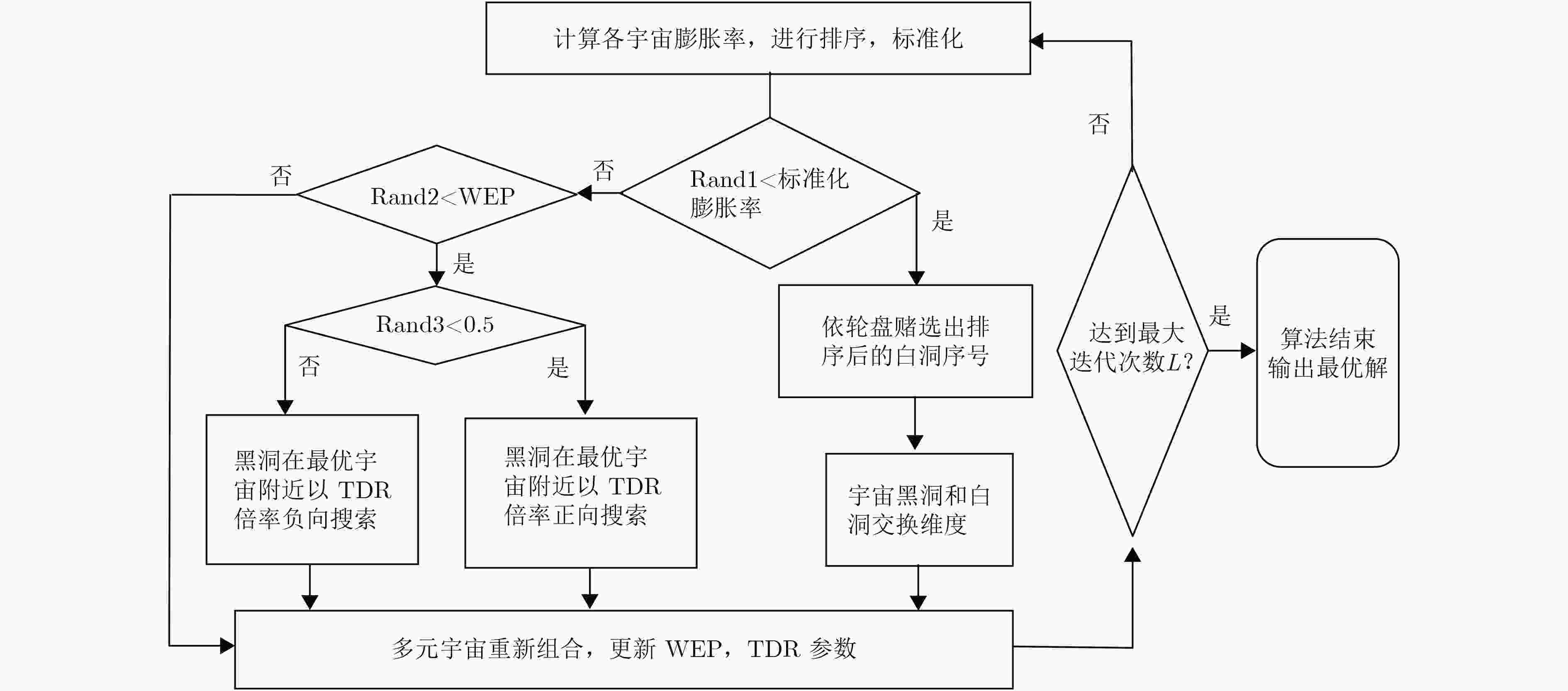
 下载:
下载:
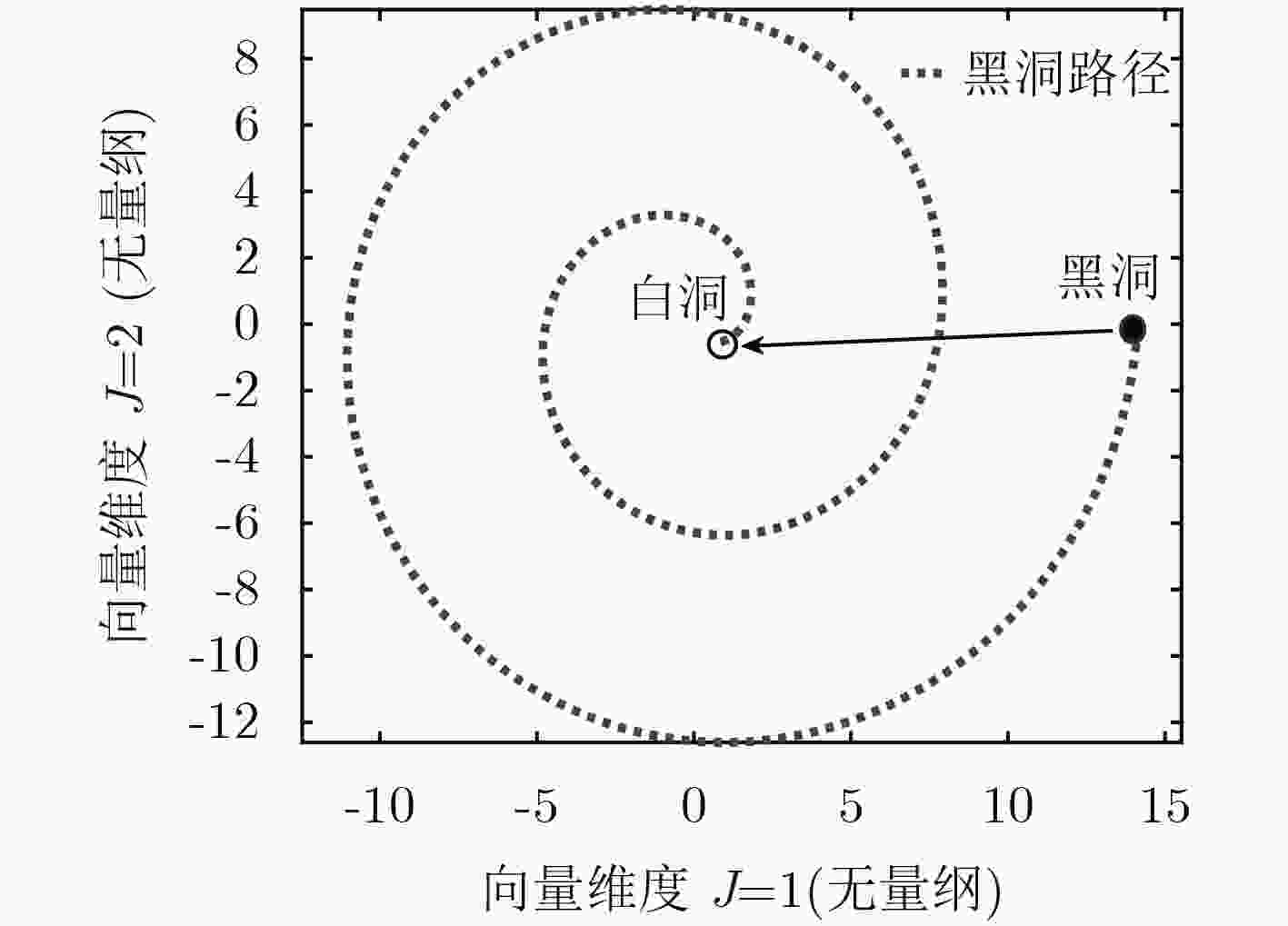


 下载:
下载:
