LiCi分组密码算法的不可能差分分析

韦永壮; 史佳利; 李灵琛

doi:10.11999/JEIT180729

LiCi分组密码算法的不可能差分分析

doi: 10.11999/JEIT180729

韦永壮^{1, 2},
史佳利^{2, 3, ,},
李灵琛^{4, 5}

1.
桂林电子科技大学广西密码学与信息安全重点实验室桂林 541004
2.
桂林电子科技大学广西无线宽带通信与信号处理重点实验室桂林 541004
3.
桂林电子科技大学广西高校云计算与复杂系统重点实验室桂林 541004
4.
中国科学院大学北京 100049
5.
中国科学院软件研究所北京 100190

基金项目: 国家自然科学基金(61572148, 61872103, 61561016), 广西研究生教育创新计划资助项目(YCBZ2018051), 获桂林电子科技大学研究生优秀学位论文培育项目(16YJPYSS12), 桂林电子科技大学研究生教育创新计划(2018YJCX45)

详细信息

作者简介:
韦永壮：男，1976年生，教授，博士生导师，研究方向为密码函数、分组密码分析

史佳利：女，1992年生，硕士生，研究方向为对称密码算法分析

李灵琛：女，1988年生，博士生，研究方向为分组密码的分析与设计

通讯作者:
史佳利　jiali00@126.com

中图分类号: TP309
计量
- 文章访问数: 3648
- HTML全文浏览量: 1599
- PDF下载量: 122
- 被引次数: 0
出版历程
- 收稿日期: 2018-07-19
- 修回日期: 2018-10-29
- 网络出版日期: 2019-03-18
- 刊出日期: 2019-07-01

Impossible Differential Cryptanalysis of LiCi Block Cipher

Yongzhuang WEI^{1, 2},
Jiali SHI^{2, 3
, ,},
Lingchen LI^{4, 5}

1.
Guangxi Key Laboratory of Cryptography and Information Security, Guilin University of Electronic Technology, Guilin 541004 ,China
2.
Guangxi Key Laboratory of Wireless Wideband Communication and Signal Processing, Guilin University of Electronic Technology, Guilin 541004 ,China
3.
Guangxi Colleges and University Key Laboratory of Cloud Computing and Complex Systems, Guilin University of Electronic Technology, Guilin 541004 ,China
4.
University of Chinese Academy of Sciences, Beijing 100049, China
5.
Institute of Software, Chinese Academy of Sciences, Beijing 100190, China

Funds: The National Natural Science Foundation of China (61572148, 61872103, 61561016), The Innovation Project of Guangxi Graduate Education (YCBZ2018051), Guilin University of Electrionic Technology Excellent Graduate Thesis Program (16YJPYSS12), The Innovation Project of Guilin University of Electrionic Technology Graduate Education (2018YJCX45)

摘要

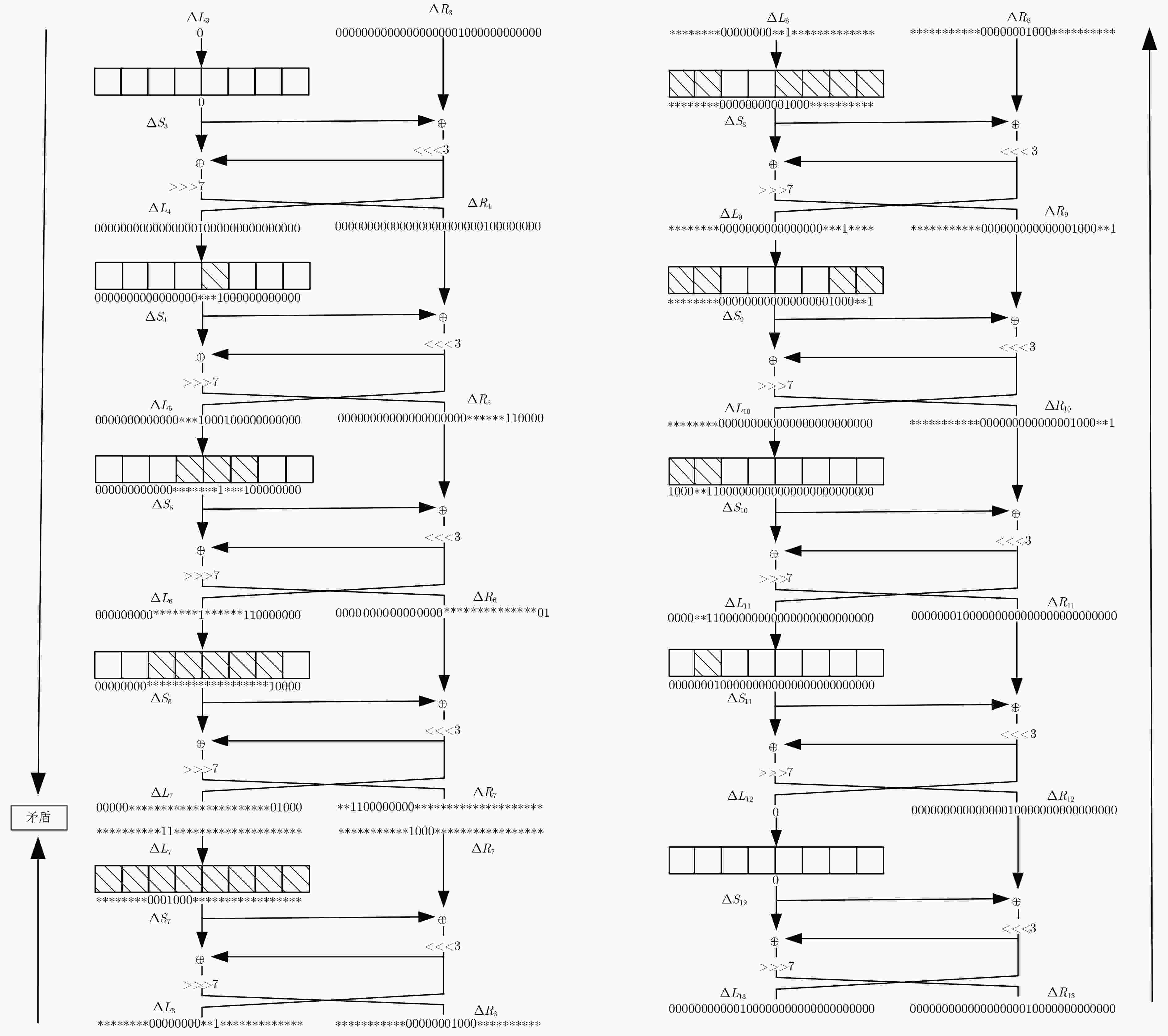
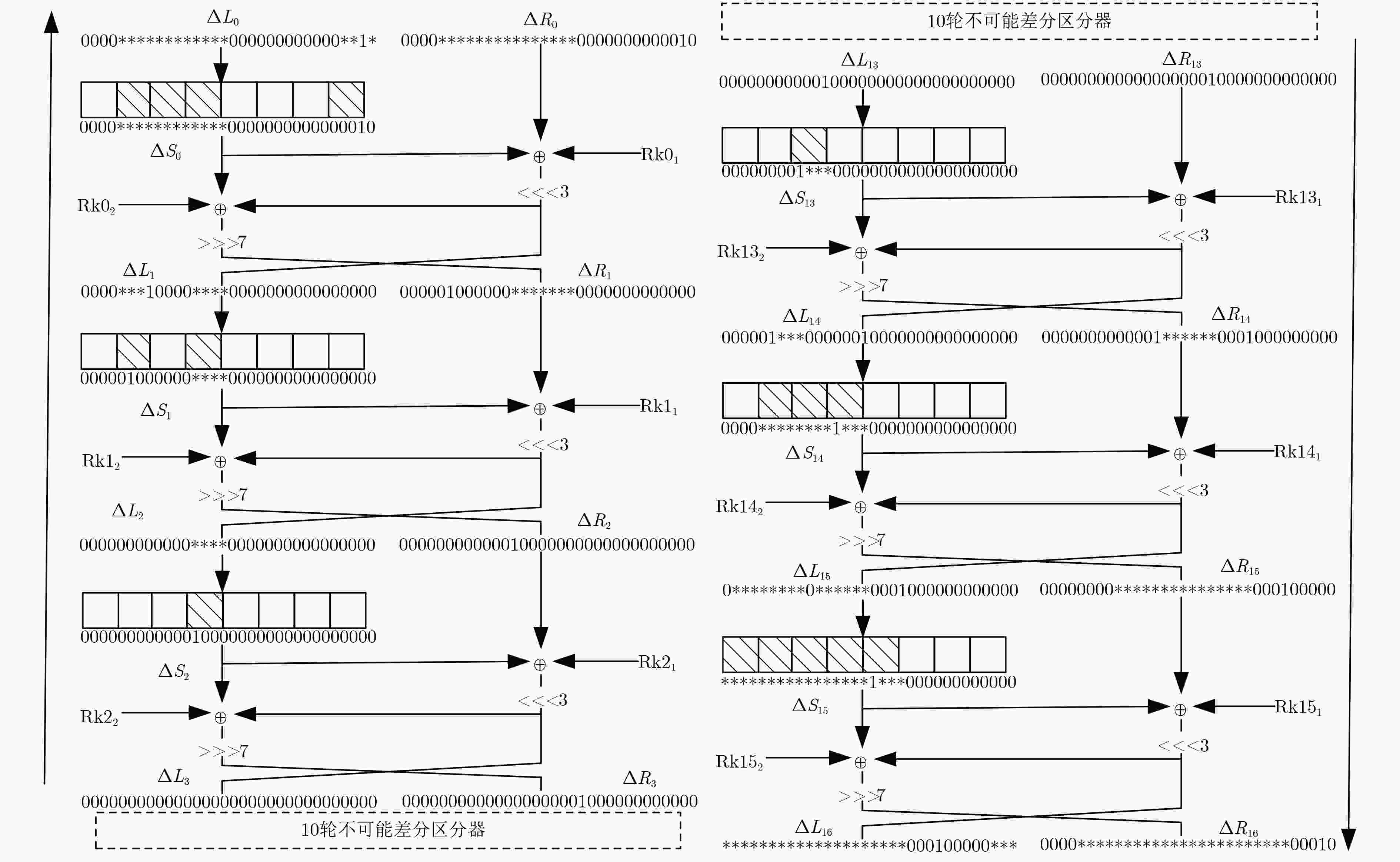
摘要: LiCi是由Patil等人(2017)提出的轻量级分组密码算法。由于采用新型的设计理念，该算法具有结构紧凑、能耗低、占用芯片面积小等优点，特别适用于资源受限的环境。目前该算法的安全性备受关注，Patil等人声称：16轮简化算法足以抵抗经典的差分攻击及线性攻击。该文基于S盒的差分特征，结合中间相遇思想，构造了一个10轮的不可能差分区分器。基于此区分器，向前后各扩展3轮，并利用密钥编排方案，给出了LiCi的一个16轮的不可能差分分析方法。该攻击需要时间复杂度约为2^83.08次16轮加密，数据复杂度约为2^59.76选择明文，存储复杂度约为2^76.76数据块，这说明16轮简化的LiCi算法无法抵抗不可能差分攻击。
- 轻量分组密码算法 /
- LiCi算法 /
- 不可能差分分析 /
- 差分特征
Abstract: LiCi algorithm is a newly lightweight block cipher. Due to its new design idea adopted by Patil et al, it has the advantages of compact design, low energy consumption and less chip area, thus is is especially suitable for resource-constrained environments. Currently, its security receives extensively attention, and Patil et al. claimed that the 16-round reduced LiCi can sufficiently resist both differential attack and linear attack. In this paper, a new 10-round impossible differential distinguisher is constructed based on the differential characteristics of the S-box and the meet-in-the-middle technique. Moreover, on the basis of this distinguisher, a 16-round impossible differential attack on LiCi is proposed by respectively extending 3-round forward and backward via the key scheduling scheme. This attack requires a time complexity of about 2^83.08 16-round encryptions, a data complexity of about 2^59.76 chosen plaintexts, and a memory complexity of 2^76.76 data blocks, which illustrates that the 16-round LiCi cipher can not resist impossible differential attack.
- Lightweight block cipher /
- LiCi cipher /
- Impossible differential cryptanalysis /
- Differential characteristic

HTML全文

图 1 LiCi算法的轮函数

下载: 全尺寸图片幻灯片

图 2 LiCi算法的10轮不可能差分路线

下载: 全尺寸图片幻灯片

图 3 LiCi算法的16轮不可能差分分析

下载: 全尺寸图片幻灯片

表 1 S盒输入/输出差分特征

输入差分	0001	0100	1000	1100	1101	**11	*1	*0	***1	***0
输出差分	1***	***1	***1	1**0	0***	0001	0010	0011	0100	0101

下载: 导出CSV

表 2 S盒输入/输出差分特征概率

输入差分	**11	*1	***1	****	0001	0***	0*	01**	*000
输出差分	0001	0010	0100	1000	1***	****	****	****	****
概率	1/4	1/8	1/8	1/16	1/8	1/2	1/2	1/4	1/8

下载: 导出CSV

表 3 不可能差分分析16轮LiCi算法的密钥恢复各步骤的时间复杂度

步骤	恢复的密钥比特	猜测比特数目	时间复杂度(单位：次16轮加密所用的时间)
(1)	–	0	${2^{m + 49}} \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 42}}$
(2)	${\rm{Rk}}{0_1}\left[ {24 \sim 21} \right]$	4	${2^{m + 21}} \times {2^4} \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 18}}$
(3)	${\rm{Rk}}{15_2}\left[ {15 \sim 12} \right]$	4	${2^{m + 18}} \times {2^4} \times {2^4} \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 19}}$
(4)	${\rm{Rk}}{15_2}\left[ {31 \sim 28} \right]$	4	${2^{m + 15}} \times {2^4} \times {2^4} \times {2^4} \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 20}}$
(5)	${\rm{Rk}}{15_2}\left[ {23 \sim 20} \right]$	4	${2^{m + 14}} \times {2^4} \times {2^4} \times {2^4} \times {2^4} \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 23}}$
(6)	${\rm{Rk}}{15_1}\left[ {16 \sim 13} \right]$, ${\rm{Rk}}{14_2}\left[ {23 \sim 20} \right]$	8	${2^{m + 13}} \times {2^4} \times {2^4} \times {2^4} \times {2^4} \times {2^8} \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 30}}$
(7)	${\rm{Rk}}{15_2}\left[ {19 \sim 16,11 \sim 9} \right]$, ${\rm{Rk}}{15_1}\left[ {12 \sim 9} \right]$, ${\rm{Rk}}{14_2}\left[ {19 \sim 16} \right]$	12	${2^{m + 10}} \times {2^{16}} \times {2^8} \times {2^{12}} \times 2 \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 40}}$
(8)	${\rm{Rk}}{15_2}\left[ {27 \sim 24} \right]$, ${\rm{Rk}}{15_1}\left[ {20 \sim 17} \right]$, ${\rm{Rk}}{14_2}\left[ {27 \sim 24} \right]$	12	${2^{m + 7}} \times {2^{24}} \times {2^{12}} \times {2^{12}} \times 2 \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 49}}$
(9)	${\rm{Rk}}{15_2}\left[ {8 \sim 6} \right]$, ${\rm{Rk}}{15_1}\left[ {8 \sim 6} \right]$, ${\rm{Rk}}{15_2}\left[ {15 \sim 13} \right]$, ${\rm{Rk}}{14_1}\left[ {16 \sim 13} \right]$	10	${2^{m + 5}} \times {2^{24}} \times {2^{12}} \times {2^{12}} \times {2^{10}} \times 2 \times \frac{1}{{8 \times 16}} = {2^{{{m}} + 56}}$
(10)	${\rm{Rk}}{0_1}\left[ {20 \sim 9} \right]$, ${\rm{Rk}}{0_2}\left[ {23 \sim 20} \right]$, ${\rm{Rk}}{1_1}\left[ {16 \sim 13} \right]$	20	${2^{m{\rm{ - }}16}} \times {2^{58}} \times {2^{20}} \times 3 \times \frac{1}{{8 \times 16}} + {2^{74}} = {2^{{{m}} + 56.58}} + {2^{74}}$

下载: 导出CSV

表 4 LiCi算法的攻击结果对比

分析方法	攻击轮数	选择明文量	时间复杂度	存储复杂度	参考文献
线性分析	16	2¹⁰⁶	–	–	文献[10]
差分分析	16	2⁹⁶	–	–	文献[10]
不可能差分分析	16	2^59.76	2^83.08	2^76.76	本文

下载: 导出CSV

参考文献(19)

BIRYUKOV A and PERRIN L. State of the art in lightweight symmetric cryptography[R]. Cryptology ePrint Archive: Report 2017/511, 2017: 1–11.

GUO Jian, PEYRIN T, POSCHMANN A, et al. The LED block cipher[C]. Proceedings of the 13th International Workshop on Cryptographic Hardware and Embedded Systems, Nara, Japan, 2011: 326–341.

BOGDANOV A, KNUDSEN L R, LEANDER G, et al. PRESENT: An ultra-lightweight block cipher[C]. Proceedings of 9th International Workshop on Cryptographic Hardware and Embedded Systems, Vienna, Austria, 2007: 450–466.

BANIK S, PANDEY S K, PEYRIN T, et al. GIFT: A small present[C]. Proceedings of the 19th International Conference on Cryptographic Hardware and Embedded Systems, Taipei, China, 2017: 321–345.

BANIK S, BOGDANOV A, ISOBE T, et al. Midori: A block cipher for low energy[C]. Proceedings of the 21st International Conference on the Theory and Application of Cryptology and Information Security, Auckland, New Zealand, 2015: 411–436.

WU Wenling and ZHANG Lei. LBlock: A lightweight block cipher[C]. Proceedings of the 9th International Conference on Applied Cryptography and Network Security, Nerja, Spain, 2011: 327–344.

国家商用密码管理办公室. 无线局域网产品使用的SMS4密码算法[EB/OL]. http://www.oscca.gov.cn/sca/c100061/201611/1002423/files/330480f731f64e1ea75138211ea0dc27.pdf, 2018.

Office of State Commercial Cipher Administration. Block cipher for WLAN products-SMS4[EB/OL]. http://www.oscca.gov.cn/sca/c100061/201611/1002423/files/330480f731f64e1ea75138211ea0dc27.pdf, 2018.

BEAULIEU R, TREATMAN-CLARK S, SHORS D, et al. The SIMON and SPECK lightweight block ciphers[C]. Proceedings of the 52nd ACM/EDAC/IEEE Design Automation Conference, San Francisco, USA, 2015: 1–6.

AOKI K, ICHIKAWA T, KANDA M, et al. Camellia: A 128-bit block cipher suitable for multiple platforms-design and analysis[C]. Proceedings of the 7th Annual International Workshop on Selected Areas in Cryptography, Ontario, Canada, 2000: 39–56.

PATIL J, BANSOD G, and KANT K S. LiCi: A new ultra-lightweight block cipher[C]. Proceedings of 2017 International Conference on Emerging Trends & Innovation in ICT, Pune, India, 2017: 40–45.

KNUDSEN L R. DEAL-a 128-bit block cipher[R]. Technical Report, 1998.

BIHAM E, BIRYUKOV A, and SHAMIR A. Cryptanalysis of Skipjack Reduced to 31 Rounds Using Impossible Differentials[M]. Berlin, Germany, 1999: 12–23.

BIHAM E and SHAMIR A. Differential cryptanalysis of DES-like cryptosystems[C]. Proceedings of the 10th Annual International Cryptology Conference on Advances in Cryptology, 1991: 2–21.

TJUAWINATA I, HUANG Tao, and WU Hongjun. Improved differential cryptanalysis on generalized feistel schemes[C]. Proceedings of the 18th International Conference on Cryptology in India, Chennai, India, 2017: 302–324.

LIU Ya, GU Dawu, LIU Zhiqiang, et al. Impossible differential attacks on reduced-round LBlock[C]. Proceedings of the 8th International Conference on Information Security Practice and Experience, Hangzhou, China, 2012: 97–108.

KONDO K, SASAKI Y, TODO Y, et al. Analyzing key schedule of SIMON: Iterative key differences and application to related-key impossible differentials[C]. Proceedings of the 12th International Workshop on Security, Hiroshima, Japan, 2017: 141–158.

MEHRDAD A, MOAZAMI F, and SOLEIMANY H. Impossible differential cryptanalysis on Deoxys-BC-256[R]. Cryptology ePrint Archive: Report 2018/048, 2018.

SHAHMIRZADI A R, AZIMI S A, SALMASIZADEH M, et al. Impossible differential cryptanalysis of reduced-round Midori64 block cipher[J]. ISeCure, 2018, 10(1): 3–14.

TEZCAN C. Improbable differential attacks on Present using undisturbed bits[J]. Journal of Computational and Applied Mathematics, 2014, 259: 503–511. doi: 10.1016/j.cam.2013.06.023

施引文献

资源附件(0)

访问统计