Polar Adaptive Successive Cancellation List Decoding Based on Segmentation Cyclic Redundancy Check
-
摘要: 针对极化码连续取消列表(SCL)译码算法为获取较好性能而采用较多的保留路径数,导致译码复杂度较高的缺点,自适应SCL译码算法虽然在高信噪比下降低了一定的计算量,却带来了较高的译码延时。根据极化码的顺序译码结构,该文提出了一种分段循环冗余校验(CRC)与自适应选择保留路径数量相结合的SCL译码算法。仿真结果表明,与传统CRC辅助SCL译码算法、自适应SCL译码算法相比,该算法在码率R=0.5时,低信噪比下(–1 dB)复杂度降低了约21.6%,在高信噪比下(3 dB)复杂度降低了约64%,同时获得较好的译码性能。Abstract: Considering the problem that using a large number of reserved paths causes higher complexity in order to obtain better performance for polar code Successive Cancellation List (SCL) decoding, the adaptive SCL decoding algorithm at a high Signal to Noise Ratio (SNR) reduces a certain amount of calculations, however, brings a higher decoding delay. According to the order of polar code decoding, an SCL decoding algorithm combining segmentation Cyclic Redundancy Check (CRC) with adaptively selecting the number of reserved paths is proposed. The simulation results show that compared with the traditional CRC-assisted SCL decoding algorithm and adaptive-SCL algorithm, when the code rate is R=0.5, the complexity under low SNR (–1 dB) is reduced by about 21.6%, and the complexity at high SNR (3 dB) is reduced by about 64%, at the same time, better decoding performance is obtained.
-
表 1 仿真参数
仿真参数 具体内容 编码结构 ${G_N} = {F^{ \otimes n}}$ 信道环境 AWGN 调制方式 BPSK 子信道置信序列构造法 DE-GA 译码算法 CA-SCL, AD-SCL, SCAD-SCL 表 2 R=0.5时不同算法复杂度比较
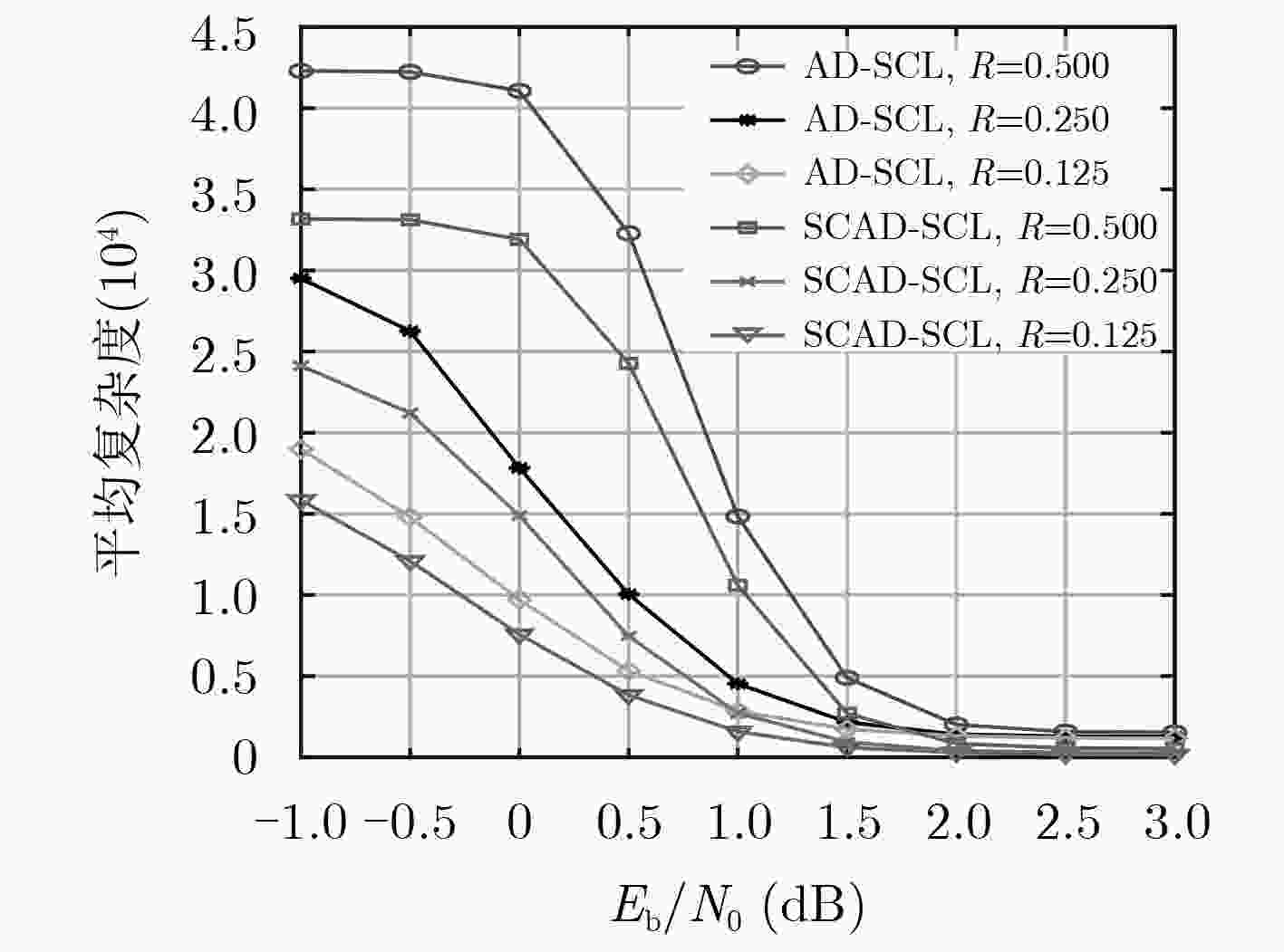
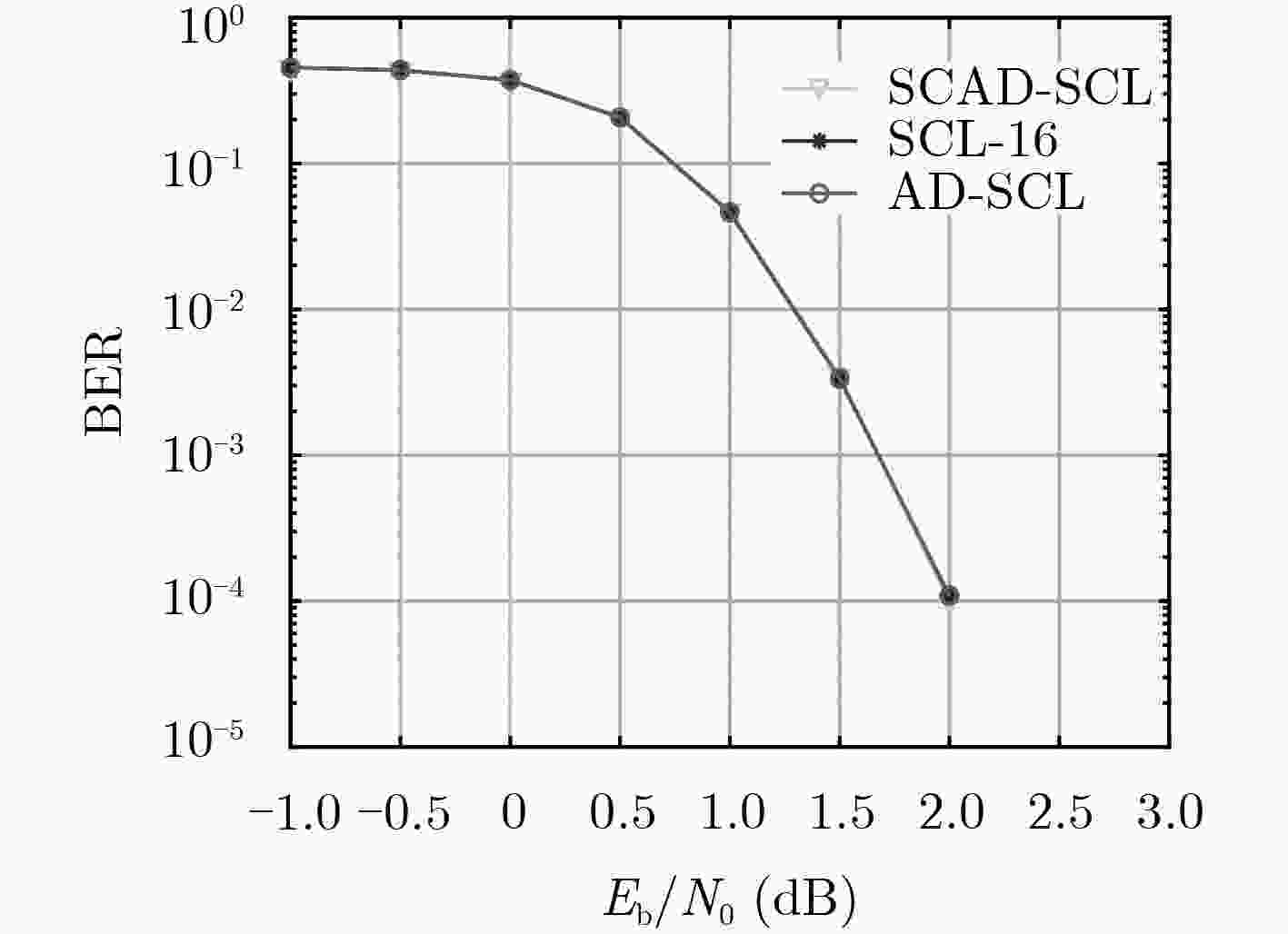
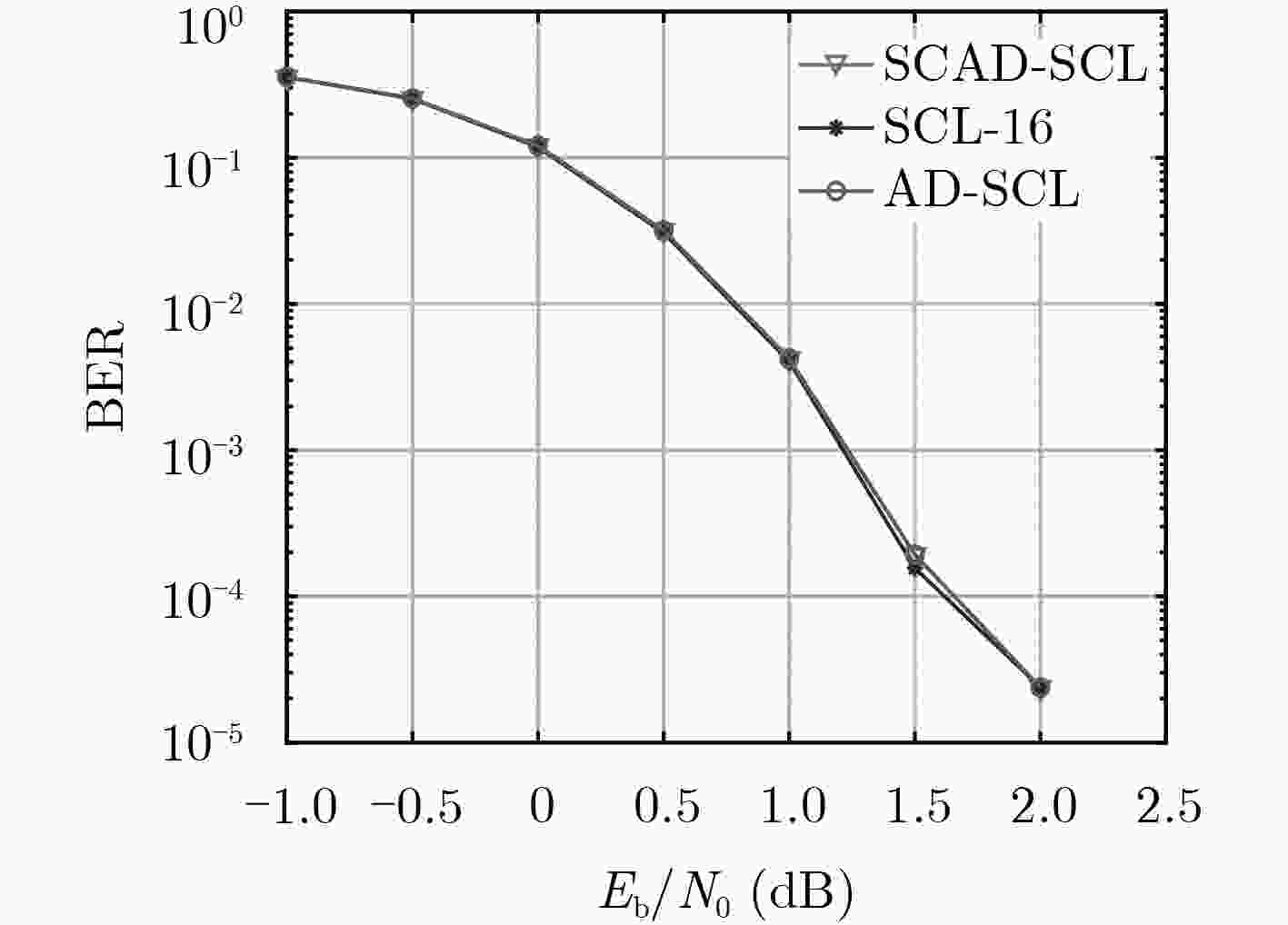
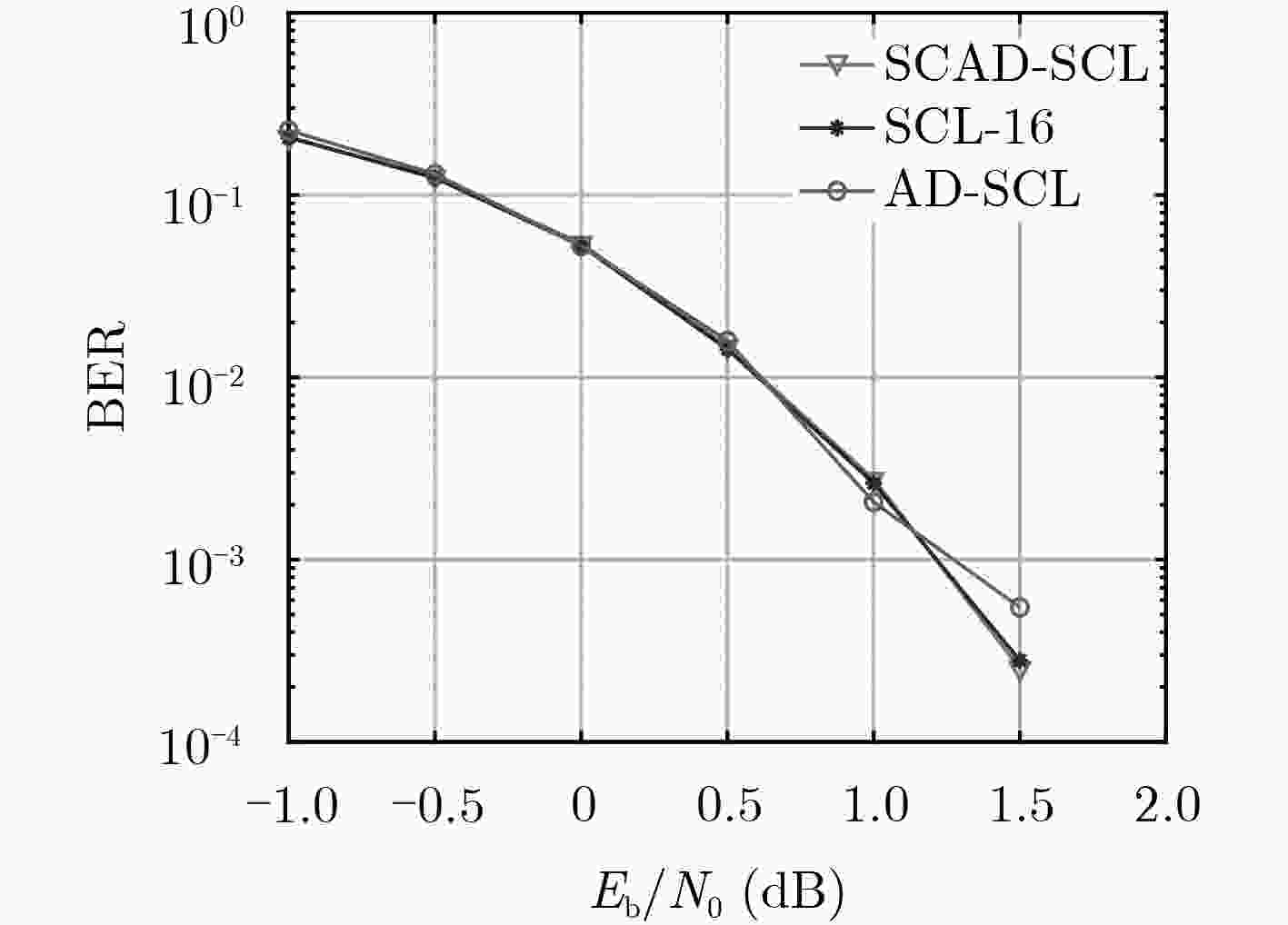
${E_b}/{N_0}$ (dB) –1.0 –0.5 0 0.5 1.0 1.5 2.0 2.5 3.0 AD-SCL 42304 42239 40850 32248 14153 4648 2034 1588 1536 SCAD-SCL 33177 33120 31918 24274 10590 2696 837 571 538 -
ARIKAN E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051–3073. doi: 10.1109/TIT.2009.2021379 ARIKAN E and TELATAR E. On the rate of channel polarization[C]. Proceedings of 2009 IEEE International Symposium on Information Theory, Seoul, South Korea, 2009: 1493–1495. ZHANG Chuan and PARHI K K. Low-latency sequential and overlapped architectures for successive cancellation polar decoder[J]. IEEE Transactions on Signal Processing, 2013, 61(10): 2429–2441. doi: 10.1109/TSP.2013.2251339 TAL I and VARDY A. List decoding of polar codes[C]. Proceedings of 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 2011: 1–5. ERCAN F, CONDO C, HASHEMI S A, et al. On error-correction performance and implementation of polar code list decoders for 5G[EB/OL]. http://arxiv.org/abs/1708.04706, 2017. NIU Kai and CHEN Kai. CRC-aided decoding of polar codes[J]. IEEE Communications Letters, 2012, 16(10): 1668–1671. doi: 10.1109/LCOMM.2012.090312.121501 ZHOU Huayi, ZHANG Chuan, SONG Wenqing, et al. Segmented CRC-aided SC list polar decoding[C]. Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference, Nanjing, China, 2016: 1–5. HASHEMI S A, CONDO C, and GROSS W J. Simplified successive-cancellation list decoding of polar codes[C]. Proceedings of 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 2016: 815–819. HASHEMI S A, CONDO C, and GROSS W J. Fast simplified successive-cancellation list decoding of polar codes[C]. Proceedings of 2017 IEEE Wireless Communications and Networking Conference Workshops, San Francisco, USA, 2017: 1–6. LI Bin, SHEN Hui, and TSE D. An adaptive successive cancellation list decoder for polar codes with cyclic redundancy check[J]. IEEE Communications Letters, 2012, 16(12): 2044–2047. doi: 10.1109/LCOMM.2012.111612.121898 MORI R and TANAKA T. Performance of polar codes with the construction using density evolution[J]. IEEE Communications Letters, 2009, 13(7): 519–521. doi: 10.1109/LCOMM.2009.090428 WU Daolong, LI Ying, and SUN Yue. Construction and block error rate analysis of polar codes over AWGN channel based on Gaussian approximation[J]. IEEE Communications Letters, 2014, 18(7): 1099–1102. doi: 10.1109/LCOMM.2014.2325811 SCHURCH C. A partial order for the synthesized channels of a polar code[C]. Proceedings of 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 2016: 220–224. HE Gaoning, BELFIORE J C, LAND I, et al. Beta-expansion: a theoretical framework for fast and recursive construction of polar codes[C]. Proceedings of 2017 IEEE Global Communications Conference, Singapore, 2017: 1–6. BALATSOUKAS-STIMMING A, PARIZI M B, and BURG A. LLR-based successive cancellation list decoding of polar codes[C]. Proceedings of 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 2014: 3903–3907. VANGALA H, VITERBO E, and HONG Yi. A comparative study of polar code constructions for the AWGN channel[EB/OL]. http://arxiv.org/abs/1501.02473, 2015. -






 下载:
下载:





 下载:
下载:
