Channel Estimation Algorithm Using Temporal-spatial Structure for Up-link of Massive MIMO Systems
-
摘要:
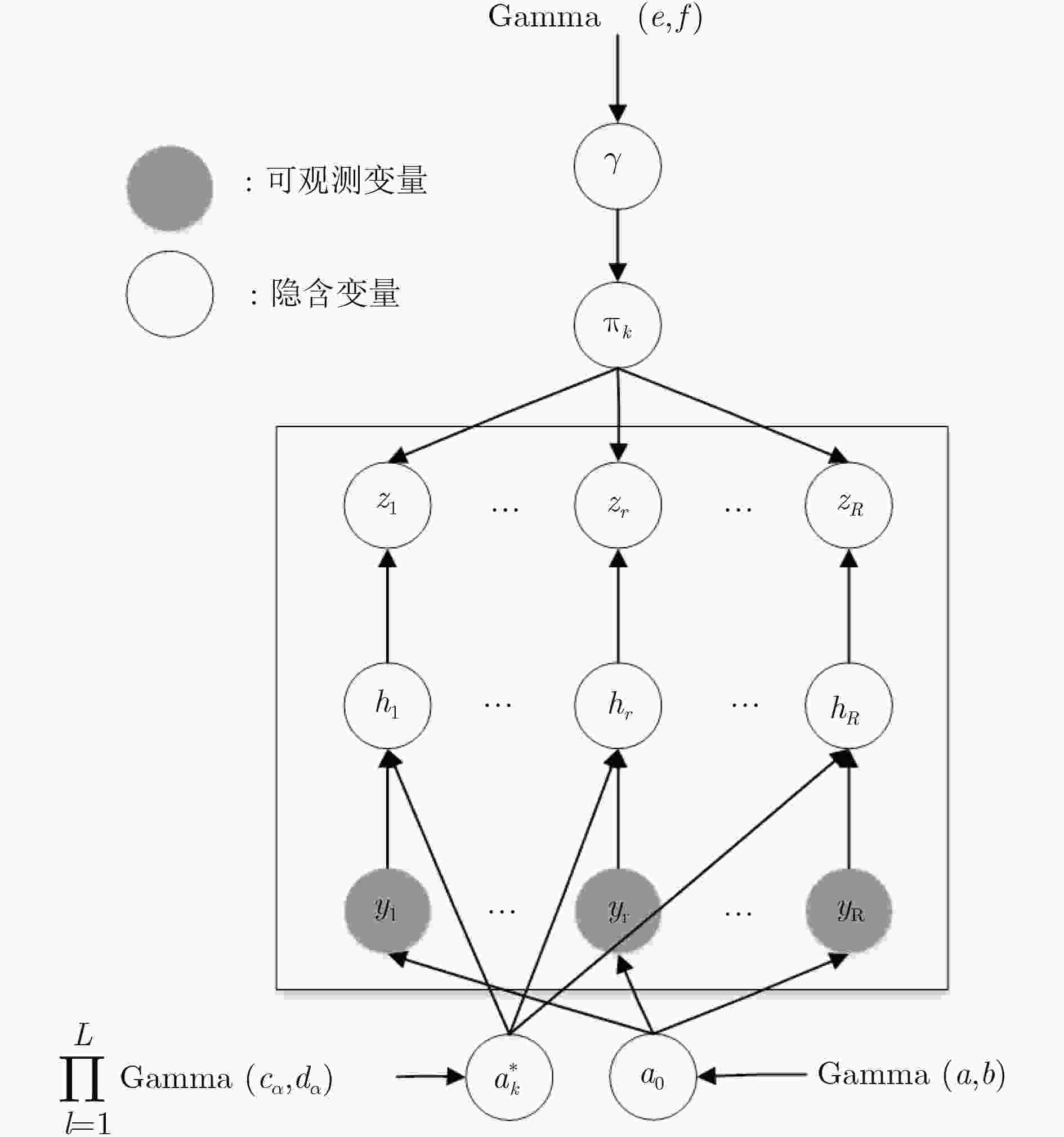
针对大规模多入多出(MIMO)系统上行链路非平稳空间相关信道的估计问题,该文利用信道的时间-空间2维稀疏结构信息,应用狄利克雷过程(DP)和变分贝叶斯推理(VBI),设计了一种低导频开销和计算复杂度的信道估计迭代算法,提高了信道估计精度。由于平稳空间相关信道难以适用于大规模MIMO系统,该文借助于狄利克雷过程构建了非平稳空间相关信道先验模型,可将具有空间关联的多个物理信道映射为具有相同时延结构的概率信道,并应用变分贝叶斯推理设计了低导频开销和计算复杂度的信道估计迭代算法。实验结果验证了所提算法的有效性,且具有对系统关键参数鲁棒性的优点。
Abstract:To deal with the estimation problem of non-stationary channel in massive Multiple-Input Multiple-Output (MIMO) up-link, the 2D channels’ sparse structure information in temporal-spatial domain is used, to design an iterative channel estimation algorithm based on Dirichlet Process (DP) and Variational Bayesian Inference (VBI), which can improve the accuracy under a lower pilot overhead and computation complexity. On account of that the stationary channel models is not suitable for massive MIMO systems anymore, a non-stationary channel prior model utilizing Dirichlet Process is constructed, which can map the physical spatial correlation channels to a probabilistic channel with the same sparse temporal vector. By applying VBI technology, a channel estimation iteration algorithm with low pilot overhead and complexity is designed. Experiment results show the proposed channel method has a better performance on the estimation accuracy than the state-of-art method, meanwhile it works robustly against the dynamic system key parameters.
-
表 1 信道估计算法的计算复杂度
算法 复杂度 本文方法 $\cal{O}\left( {R{L^{\rm{2}}}} \right)$ FSBL $\cal{O}\left( {R{N_{\rm{p}}}L} \right)$ BSBL $\cal{O}\left( {{{\left( {RL} \right)}^3}} \right)$ SABMP $\cal{O}\left( {R{N_{\rm{p}}}{L^2}} \right)$ 表 2 大规模MIMO-OFDM系统参数
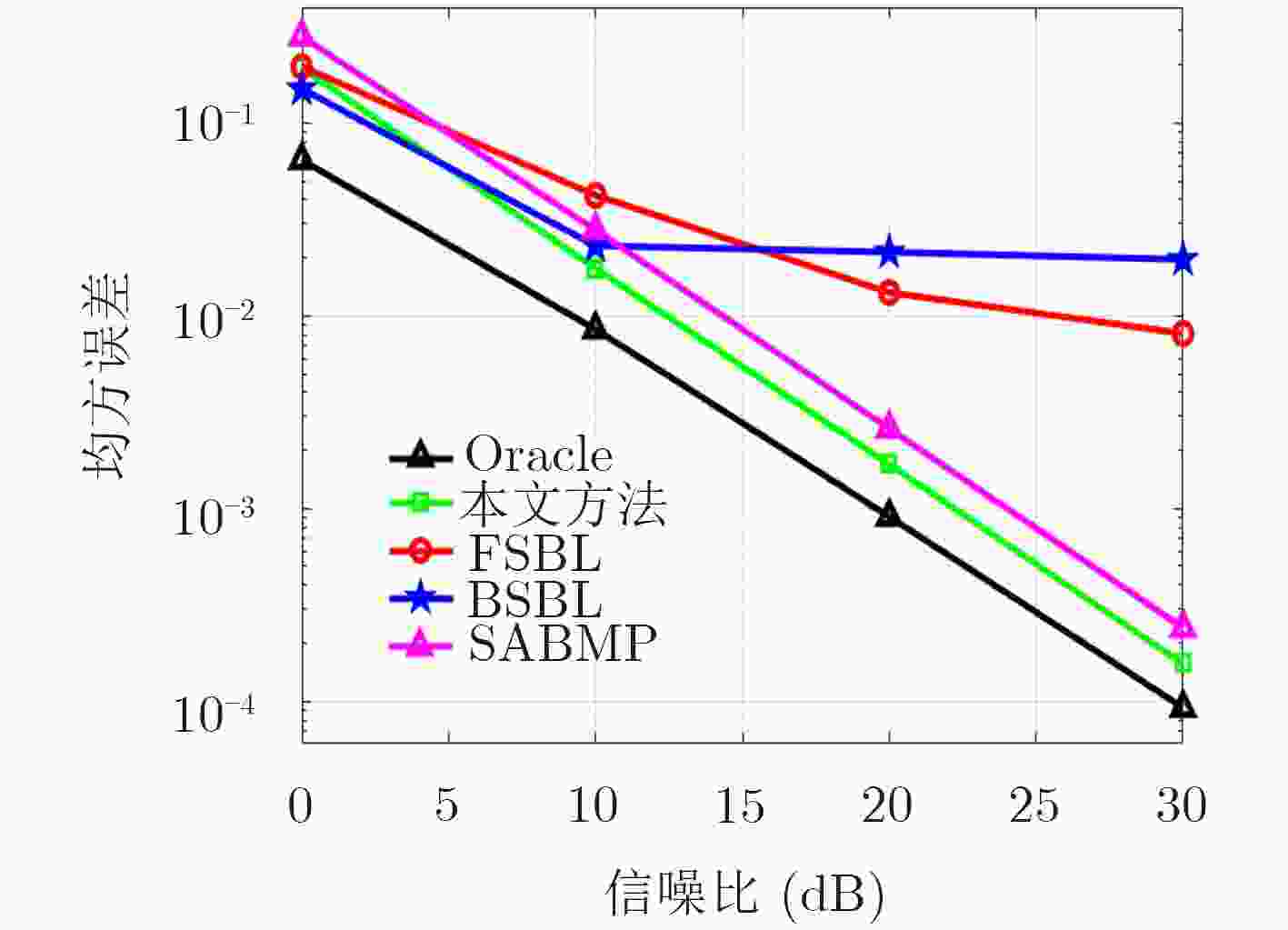
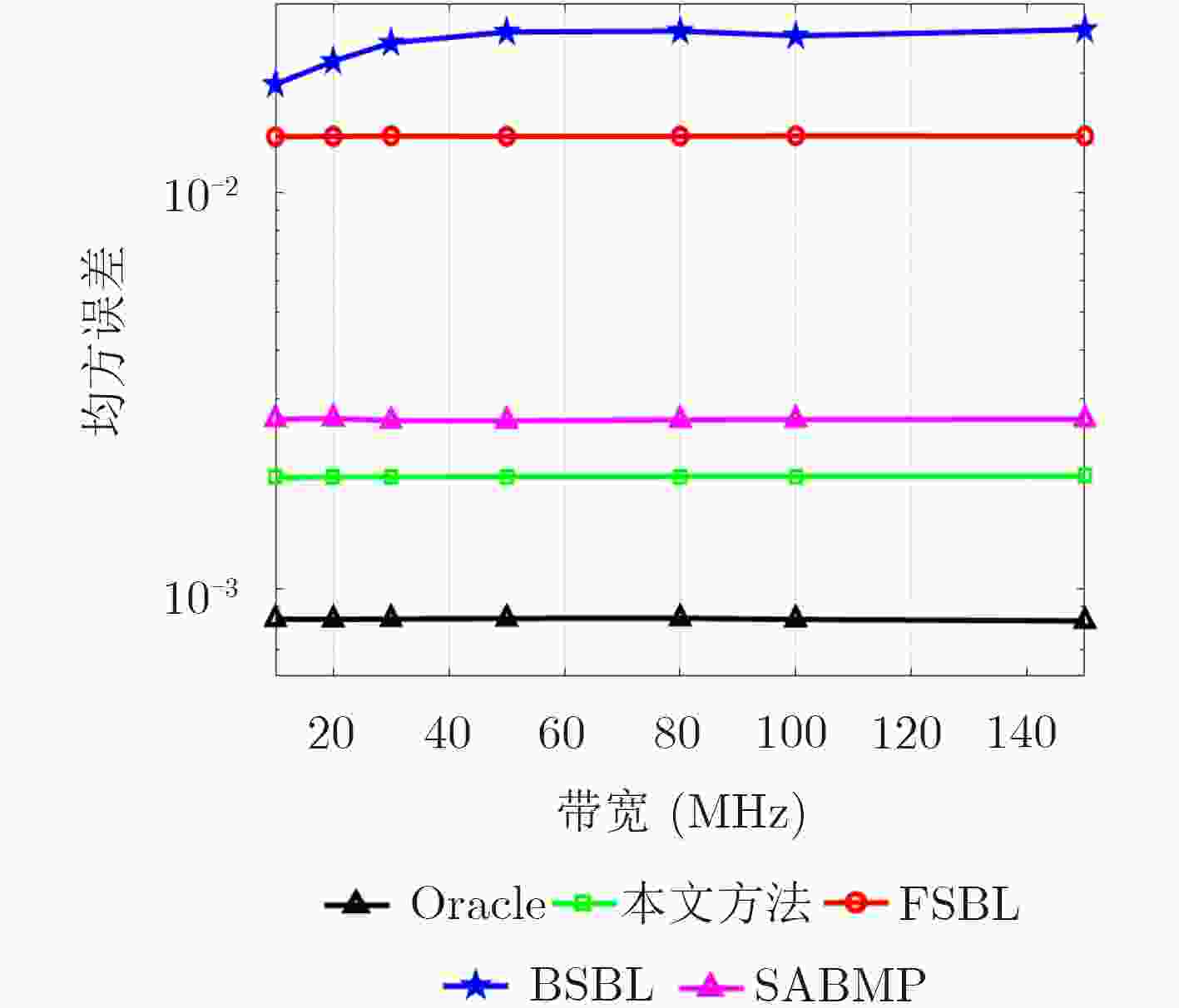
参数名 参数意义 数值 R 基站侧天线数 128 fc 载波中心频率 2.6 GHz N OFDM总子载波数 1024 Np 信道估计占用子载波数 64 BW 用户带宽 10~100 MHz Q QAM调制阶数 4 L 信道抽头个数 64 Ip 多径总径数 20 -
MARZETTA T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE Transactions on Wireless Communications, 2010, 9(11): 3590–3600. doi: 10.1109/TWC.2010.092810.091092 RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO: opportunities and challenges with very large array[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40–60. doi: 10.1109/MSP.2011.2178495 PAYAMI S and TUFVESSON F. Channel measurements and analysis for very large array systems at 2.6 GHz[C]. The 6th European Conference on Antennas and Propagation, Prague, Czech Republic, 2012: 433–437. GAO Xiang, TUFVESSON F, and EDFORS O. Massive MIMO channels - Measurements and models[C]. Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 2013: 280–284. WU Shangbin, WANG Chengxiang, HAAS H, et al. A Non-stationary wideband channel model for massive MIMO communication systems[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1434–1446. doi: 10.1109/TWC.2014.2366153 NGUYEN S. Compressive sensing for multi-channel and large-scale MIMO networks[D]. [Ph.D. dissertation], Concordia University, 2013. QI Chenhao, HUANG Yongming, JIN Shi, et al. Sparse channel estimation based on compressed sensing for massive MIMO systems[C]. 2015 IEEE International Conference on Communications, London, UK, 2015: 4558–4563. CHEN Lei, LIU An, and YUAN Xiaojun. Structured turbo compressed sensing for massive MIMO channel estimation using a Markov prior[J]. IEEE Transactions on Vehicular Technology, 2018, 67(5): 4635–4639. doi: 10.1109/TVT.2017.2787708 HOU Weikun and LIM C W. Structured compressive channel estimation for large-scale MISO-OFDM systems[J]. IEEE Communications Letters, 2014, 18(5): 765–768. doi: 10.1109/LCOMM.2014.030714.132630. NAN Yang, ZHANG Li, and SUN Xin. Weighted compressive sensing based uplink channel estimation for time division duplex massive Multi-Input Multi-Output systems[J]. IET Communications, 2017, 11(3): 355–361. doi: 10.1049/iet-com.2016.0625 MASOOD M, AFIFY L H, and AL-NAFFOURI T Y. Efficient coordinated recovery of sparse channels in massive MIMO[J]. IEEE Transactions on Signal Processing, 2015, 63(1): 104–118. doi: 10.1109/TSP.2014.2369005 PEDERSEN N L, MANCHÓN C N, and FLEURY B H. A fast iterative Bayesian inference algorithm for sparse channel estimation[C]. 2013 IEEE International Conference on Communications, Budapest, Hungary, 2013: 4591–4596. MA Jianpeng, LI Hongyan, ZHANG Shun, et al. Sparse Bayesian learning for the channel statistics of the massive MIMO systems[C]. 2017 IEEE Global Communications Conference, Singapore, 2017: 1–6. GUI Guan, XU Li, and SHAN Lin. Block Bayesian sparse learning algorithms with application to estimating channels in OFDM systems[C]. 2014 International Symposium on Wireless Personal Multimedia Communications, Sydney, Australia, 2014: 238–242. CHENG Xiantao, SUN Jingjing, and LI Shaoqian. Channel estimation for FDD multi-user massive MIMO: a variational Bayesian inference-based approach[J]. IEEE Transactions on Wireless Communications, 2017, 16(11): 7590–7602. doi: 10.1109/TWC.2017.2751046 TIPPING M. Sparse Bayesian learning and the relevance vector machine[J]. The Journal of Machine Learning Research, 2001, 1: 211–244. doi: 10.1162/15324430152748236 BLEI D M and JORDAN M I. Variational inference for dirichlet process mixtures[J]. Bayesian Analysis, 2006, 1(1): 121–143. doi: 10.1214/06-BA104 梅素玉, 王飞, 周水庚. 狄利克雷过程混合模型、扩展模型及应用[J]. 科学通报, 2012, 57(34): 3243–3257.MEI Suyu, WANG Fei, and ZHOU Shuigeng. Dirichlet process mixture model, extensions and applications[J]. Chinese Science Bulletin (Chinese Version) , 2012, 57(34): 3243–3257. WANG Lu, ZHAO Lifan, BI Guoan, et al. Novel wideband DOA estimation based on sparse bayesian learning with dirichlet process priors[J]. IEEE Transactions on Signal Processing, 2016, 64(2): 275–289. doi: 10.1109/TSP.2015.2481790 TSE D and VISWANATH P. Fundamentals of Wireless Communication[M]. Cambridge: Cambridge University, 2004: 32–50, 348–352. -





 下载:
下载:


 下载:
下载:
