A Moving-targets Detection Algorithm for Spaceborne SAR System Based on Two-dimensional Velocity Search Method
-
摘要: 采用传统SAR成像方法对星载SAR地面运动目标进行成像处理时,运动目标通常会处于散焦状态,导致运动目标检测性能下降。该文结合RD算法,提出一种基于2维速度搜索的星载SAR运动目标检测算法,通过对运动目标距离向速度和方位向速度进行遍历来匹配运动目标多普勒参数,提取不同搜索速度下运动目标的最强幅度值用于恒虚警检测,可以提高运动目标的检测概率。仿真结果验证了该方法的可行性和有效性。Abstract: The moving target component is often defocused in spaceborne SAR images. Therefore, the moving target detection performance is affected depending on the degree of defocusing. Combined with the RD algorithm, a moving-targets detection algorithm for spaceborne SAR based on a two-dimensional velocity search is proposed. Through velocity search on the distance direction and the azimuth direction, the Doppler parameters of possible moving targets can be matched. Then the strongest value among all the searching velocity results for each pixel is used for Constant False Alarm Rate(CFAR) detector. This core process can improve the detection performance of moving target component. Simulation results validate the effectiveness of the proposed method.
-
Key words:
- Synthetic Aperture Radar(SAR) /
- Moving target detection /
- RD algorithm /
- Velocity search
-
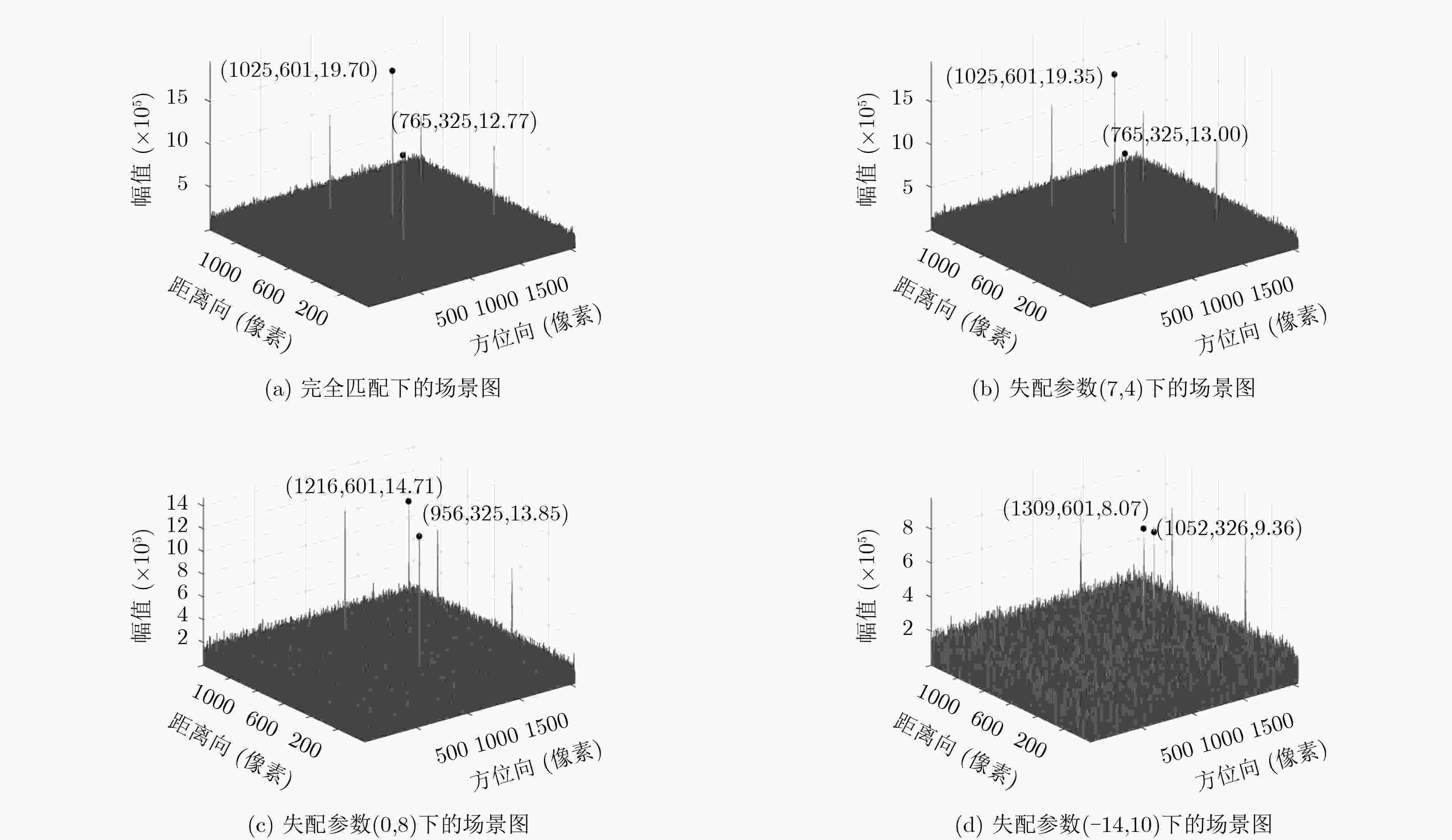
表 1 不同参数下,运动目标成像性能分析
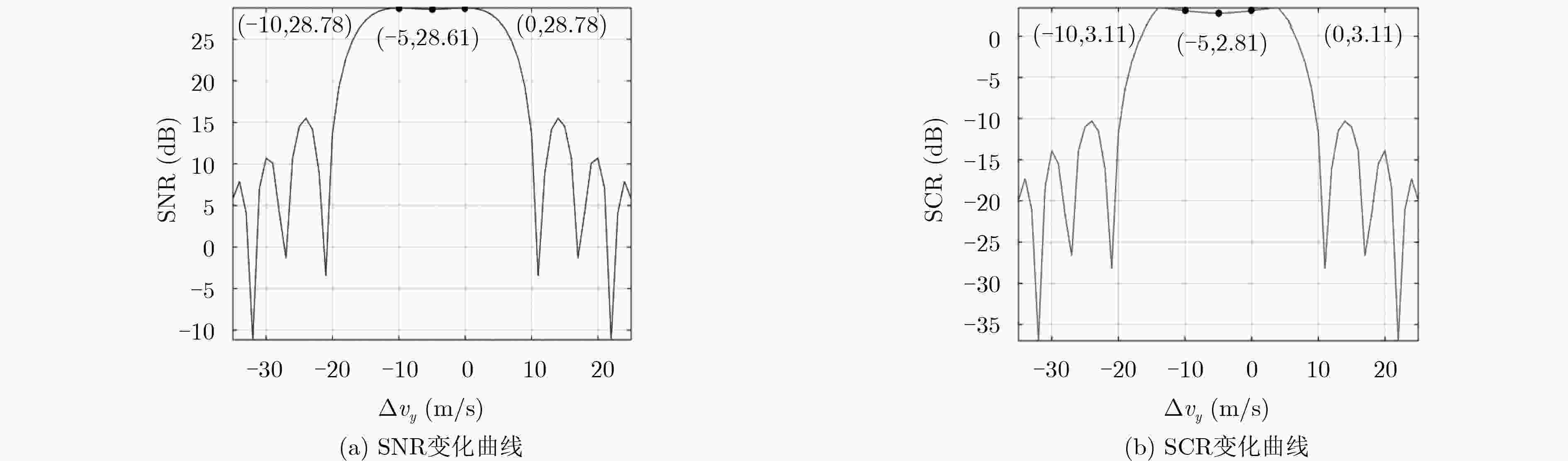
不同参数 完全匹配(9,4) 失配(7,4) 失配(0,8) 失配(–14,10) SNR (dB) 30.00 29.92 27.35 21.17 SCR (dB) 3.75 3.41 0.67 –2.26 -
李春升, 王伟杰, 王鹏波, 等. 星载SAR技术的现状与发展趋势[J]. 电子与信息学报, 2016, 38(1): 229–240. doi: 10.11999/JEIT151116LI Chunsheng, WANG Weijie, WANG Pengbo, et al. Current situation and development trends of spaceborne SAR technology[J]. Journal of Electronics &Information Technology, 2016, 38(1): 229–240. doi: 10.11999/JEIT151116 韦北余, 朱岱寅, 吴迪. 一种基于动目标聚焦的SAR-GMTI方法[J]. 电子与信息学报, 2016, 38(7): 1738–1744. doi: 10.11999/JEIT151036WEI Beiyu, ZHU Daiyin, and WU Di. A SAR-GMTI approach based on moving target focusing[J]. Journal of Electronics &Information Technology, 2016, 38(7): 1738–1744. doi: 10.11999/JEIT151036 ENTZMINGER J N, FOWLER C A, and KENNEALLY W J. JointSTARS and GMTI: Past, present and future[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 748–761. doi: 10.1109/7.766956 ZHENG Hongchao, WANG Junfeng, and LIU Xiaozhao. Motion parameter estimation for multichannel SAR-GMTI systems[C]. 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–4. 郑明洁. 合成孔径雷达动目标检测和成像研究[D]. [博士论文], 中国科学院电子学研究所, 2003: 6. HUANG Yan, LIAO Guisheng, XU Jingwei, et al. GMTI and parameter estimation via time-Doppler chirp-varying approach for single-channel airborne SAR system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8): 4367–4383. doi: 10.1109/TGRS.2017.2691742 WANG Yu, CAO Yunhe, PENG Zhigang, et al. Clutter suppression and moving target imaging approach for multichannel hypersonic vehicle borne radar[J]. Digital Signal Processing, 2017, 68: 81–92. doi: 10.1016/j.dsp.2017.05.010 YAN He, ZHU Daiyin, WANG R, et al. Practical signal processing algorithm for wide-area surveillance-GMTI mode[J]. IET Radar, Sonar & Navigation, 2015, 9(8): 991–998. doi: 10.1049/iet-rsn.2014.0452 ZHANG Xuepan, LIU Lu, and ZHANG Xuejing. Parameterized pseudo-localization for accurate and efficient moving targets imaging in synthetic aperture radar[J]. Sensors, 2017, 17(8): 1714. doi: 10.3390/s17081714 LIU Congfeng and LIAO Guisheng. Canonical framework for multi-channel SAR-GMTI[J]. Journal of Systems Engineering and Electronics, 2008, 19(5): 923–928. doi: 10.1016/S1004-4132(08)60176-0 YANG Jian. SAR ground moving target indication and imaging theory[M]. YANG Jian. Study on Ground Moving Target Indication and Imaging Technique of Airborne SAR. Singapore, Springer, 2017: 13–32. WANG Xinyun, DENG Bin, WANG Hongqiang, et al. Ground moving target imaging based on motion compensation for circular SAR[C]. Proceedings of the 9th International Conference on Advanced Infocomm Technology (ICAIT), Chengdu, 2017: 372–377. 林晨晨, 黄普明, 李渝. 多通道SAR-GMTI技术的研究进展[J]. 电讯技术, 2017, 57(1): 118–126. doi: 10.3969/j.issn.1001-893x.2017.01.020LIN Chenchen, HUANG Puming, and LI Yu. Research progress in multichannel SAR-GMTI[J]. Telecommunication Engineering, 2017, 57(1): 118–126. doi: 10.3969/j.issn.1001-893x.2017.01.020 MAKHOUL E, BROQUETAS A, RODON J R, et al. A performance evaluation of SAR-GMTI missions for maritime applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2496–2509. doi: 10.1109/TGRS.2014.2360989 LV Gaohuan, WANG Junfeng, and LIU Xingzhao. Ground moving target indication in SAR images by symmetric defocusing[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 241–245. doi: 10.1109/LGRS.2012.2200232 -





 下载:
下载:






 下载:
下载:
