1.   引言

当前，电子信息技术迅速发展，射频识别(Radio Frequency IDentification, RFID)等技术广泛应用，为了在这些资源受限的环境中对数据进行加密需采用轻量级密码算法，因此具有占用资源少、功耗低、效率高、易于实现等优势的轻量级分组密码被提出并迅速成为研究热点，如LBlock^[1], MIBS^[2], PRESENT^[3]等。八阵图算法(Eight-Sided Fortress, ESF)^[4]是根据LBlock改进而得的一种轻量级分组密码算法，其整体结构与LBlock基本一致，但借鉴了PRESENT算法中P层置换的设计，利用按位置换的形式替换LBlock中4 bit为一组进行置换的形式，使得明文数据能经过少量轮变化后迅速扩散从而提高算法的扩散性与安全性。在安全性方面，算法提出者刘宣等人^[4]给出8轮不可能差分区分器，并对11轮ESF进行了不可能差分分析；陈玉磊等人^[5]利用相同的8轮区分器，通过改变轮数扩展方式以及猜测密钥的顺序，改善了11轮ESF不可能差分分析结果；高红杰等人^[6]同样用文献[4]提出的8轮区分器，对12轮ESF进行了不可能差分分析；尹军等人^[7,8]提出15轮ESF差分活跃S盒的数量最少为19, 16轮ESF线性活跃S盒的数量最少为15，并用相关密钥差分分析得到11轮ESF相关密钥差分特征，在此基础上对13轮ESF进行了攻击。

本文使用的相关密钥不可能差分方法是将相关密钥分析和不可能差分分析相结合。相关密钥分析是由Knudsen^[9]和Biham^[10]提出的，是利用轮密钥之间的关系来恢复密钥的一种分析方法。不可能差分分析由Biham等人^[11]提出，是通过差分概率为0的差分来过滤错误密钥从而恢复正确密钥的一种攻击方法，该方法应用较为广泛，对Deoxys-BC^[12], SPECK^[13], MIBS^[14]等分组密码都有较好分析结果。通过结合这两种分析方法，可选定两个特殊的密钥差分以及明文差分使其正好抵消，致使活跃S盒个数减少且差分链长度增加，从而实现更多轮数的攻击。目前，该方法已应用于对LBlock^[15], MIBS^[16]等分组密码的安全性分析。本文利用相关密钥不可能差分方法研究对ESF的攻击，在现有不可能差分的结果上，加入相关密钥分析，通过构造11轮的相关密钥不可能差分区分器，成功实现对15轮ESF的相关密钥不可能差分攻击，此攻击不仅在攻击轮数上有所提高，恢复密钥比特数有所增加，而且时间复杂度大幅降低，数据复杂度也较为理想，是目前关于ESF算法安全性分析的最好结果。

论文的组织结构如下：第2节简要说明要使用的符号及ESF算法的基本知识；第3节给出11轮相关密钥不可能差分区分器的构造过程并详细说明恢复15轮ESF密钥的方法；第4节对全文进行总结。

2.   ESF算法简介

2.1   符号表示和基本概念

本文常用符号约定如表1所示：

表 1  符号约定

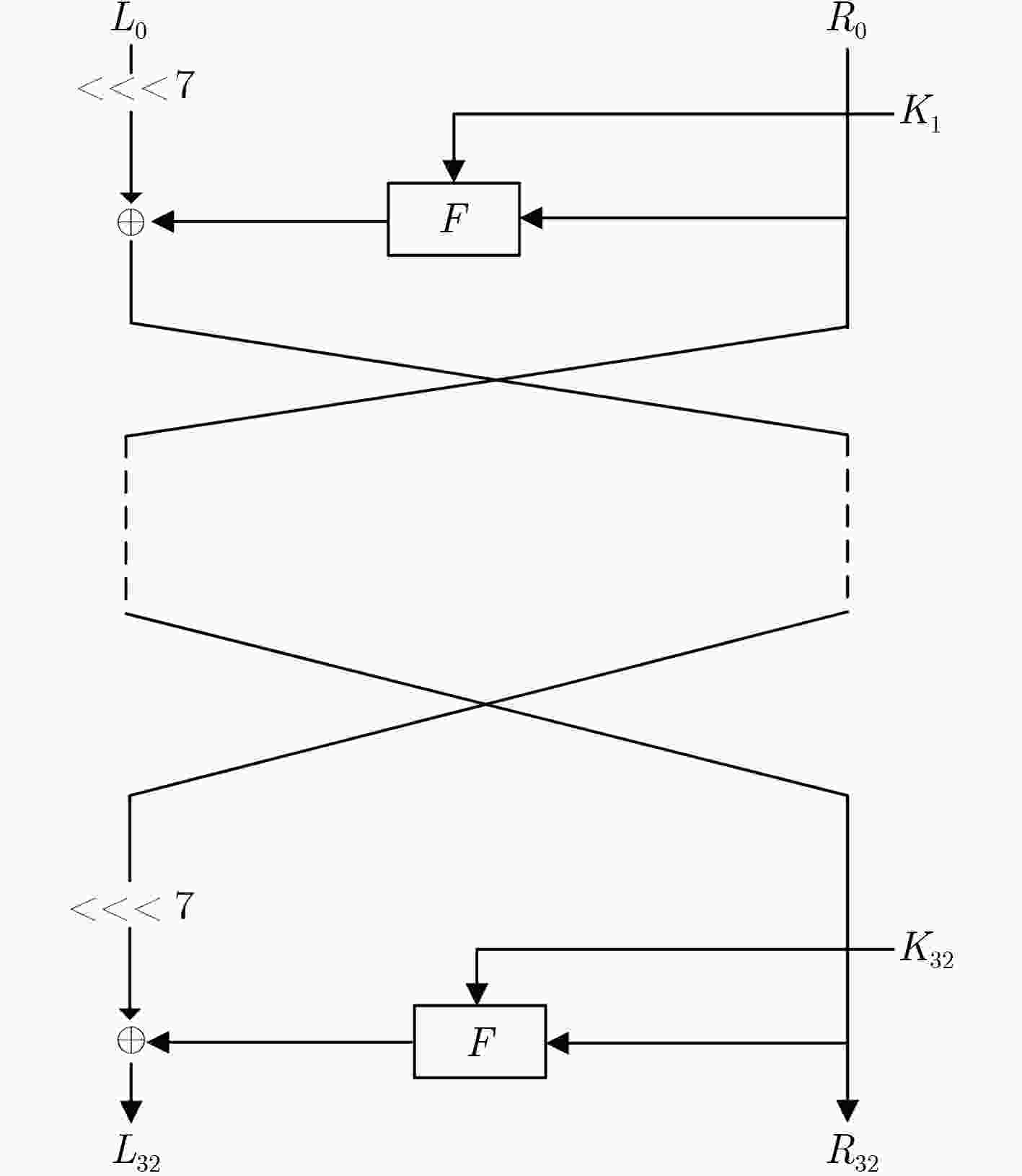
符号	意义
$K$	80 bit主密钥
${K_i}$	第$i\,$轮的32 bit轮密钥
${K_{i, j}}$	${K_i}$的第$j$个半字节
$K_{i, j}^l$	${K_{i, j}}$的第$l$位
${L_i}$	第$i\,$轮输出密文的左边32 bit
${R_i}$	第$i\,$轮输出密文的右边32 bit
$< < < 7$	循环左移7位
$\oplus$	按位异或运算符
$||$	二进制字符联接
${[i]_2}$	常数$i\,$的二进制表示

下载: 导出CSV 

| 显示表格

2.2   ESF算法简介

ESF是LBlock的改进算法，算法整体采用变体的Feistel结构，轮函数采用SPN结构。该算法分组长度和主密钥长度分别为64 bit和80 bit，采用32轮迭代。算法加密结构如图1，具体加密过程为：

图 1  ESF算法加密流程

下载: 全尺寸图片 幻灯片

(1) 输入明文${L_0}||{R_0}$；

(2) 对$i = 1, 2, ·\!·\!· , 31$执行：

　 ${L_i} = {R_{i - 1}}$，

　 ${R_i} = ({L_{i - 1}} < < < 7) \oplus F({R_{i - 1}}, {K_i})$，

　 当$i = 32$时：

　 ${L_{32}} = ({L_{31}} < < < 7) \oplus F({R_{31}}, {K_{32}})$，

　 ${R_{32}} = {R_{31}}$；

(3) 输出密文${L_{32}}||{R_{32}}$。

ESF算法轮函数F定义为：$F({R_j}, {K_j}) = P(S({R_j}$$\oplus {K_j}))$，计算流程如图2所示。轮函数为SPN结构，由3类基本变换组成：密钥加、混淆层以及P置换。

图 2  ESF算法轮函数

下载: 全尺寸图片 幻灯片

混淆层：非线性S函数由8个并行的S盒组成。

P置换：该变换为线性变换，将32 bit的$({b_{31}}||{b_{30}}||·\!·\!· {b_1}||{b_0})$映射成$({c_{31}}||{c_{30}}|| ·\!·\!· {c_1}||{c_0})$。具体定义为：$({b_{31}}||{b_{30}}|| ·\!·\!· {b_1}||{b_0}) \to ({c_{31}}||{c_{30}}|| ·\!·\!· {c_1}||{c_0})$，当$0 \le i < 8$时，$({b_{4i}}||{b_{4i + 1}}||{b_{4i + 2}}||{b_{4i + 3}}) \to ({c_i}||{c_{i + 8}}$$||{c_{i + 16}}||{c_{i + 24}})$。

2.3   ESF密钥扩展算法

ESF主密钥长度为80 bit，其密钥扩展算法采用了基于半字节的方式进行计算，每经过1次迭代寄存器会有13 bit更新。将$K = ({k_{79}}{k_{78}}·\!·\!· {k_1}{k_0})$存入寄存器，${K_1}$为最左边32 bit，轮密钥更新为：

对$i = 1, 2,·\!·\!·, 31$，重复下列操作：

(1) $K < < < 13$；

(2) $[{k_{79}}{k_{78}}{k_{77}}{k_{76}}] = {S_0}[{k_{79}}{k_{78}}{k_{77}}{k_{76}}]$，

　 $[{k_{75}}{k_{74}}{k_{73}}{k_{72}}] = {S_0}[{k_{75}}{k_{74}}{k_{73}}{k_{72}}],$

　 $[{k_{47}}{k_{46}}{k_{45}}{k_{44}}{k_{43}}] = [{k_{47}}{k_{46}}{k_{45}}{k_{44}}{k_{43}}] \oplus {[i]_2}$

(3)取最左边32 bit为子密钥${K_{i + 1}}$。

3.   ESF算法的相关密钥不可能差分分析

本节详细介绍15轮ESF的相关密钥不可能差分分析。首先构造11轮的相关密钥不可能差分区分器：$(00000000, 00000000)\nrightarrow (00000020, 00000000)$，再将此区分器向前和向后各添加2轮，实现对15轮ESF的相关密钥不可能差分攻击。

3.1   11轮ESF相关密钥不可能差分区分器

在实现相关密钥不可能差分攻击时，首先选择密钥差分。通过分析ESF密钥扩展算法可知：当一个非0密钥差分经过S盒后，再次经过S盒的间隔轮数较大，因此活跃S盒数量增长缓慢。在合适的地方引入非0密钥差分，不会使得每个轮密钥都有非0差分，平均连续两次出现非0密钥差分后出现4次全0密钥差分，由此可通过选定特殊的密钥差分，得到更长的密钥差分链。本文选择初始主密钥差分$\Delta K=\;(00000200000000000000)$，由此构造出一条低重量密钥差分链。加解密过程用到的15轮相关密钥差分由$\Delta K$扩展而得，其中“*”表示非0半字节。扩展密钥差分如表2所示。

表 2  15轮相关密钥差分路径

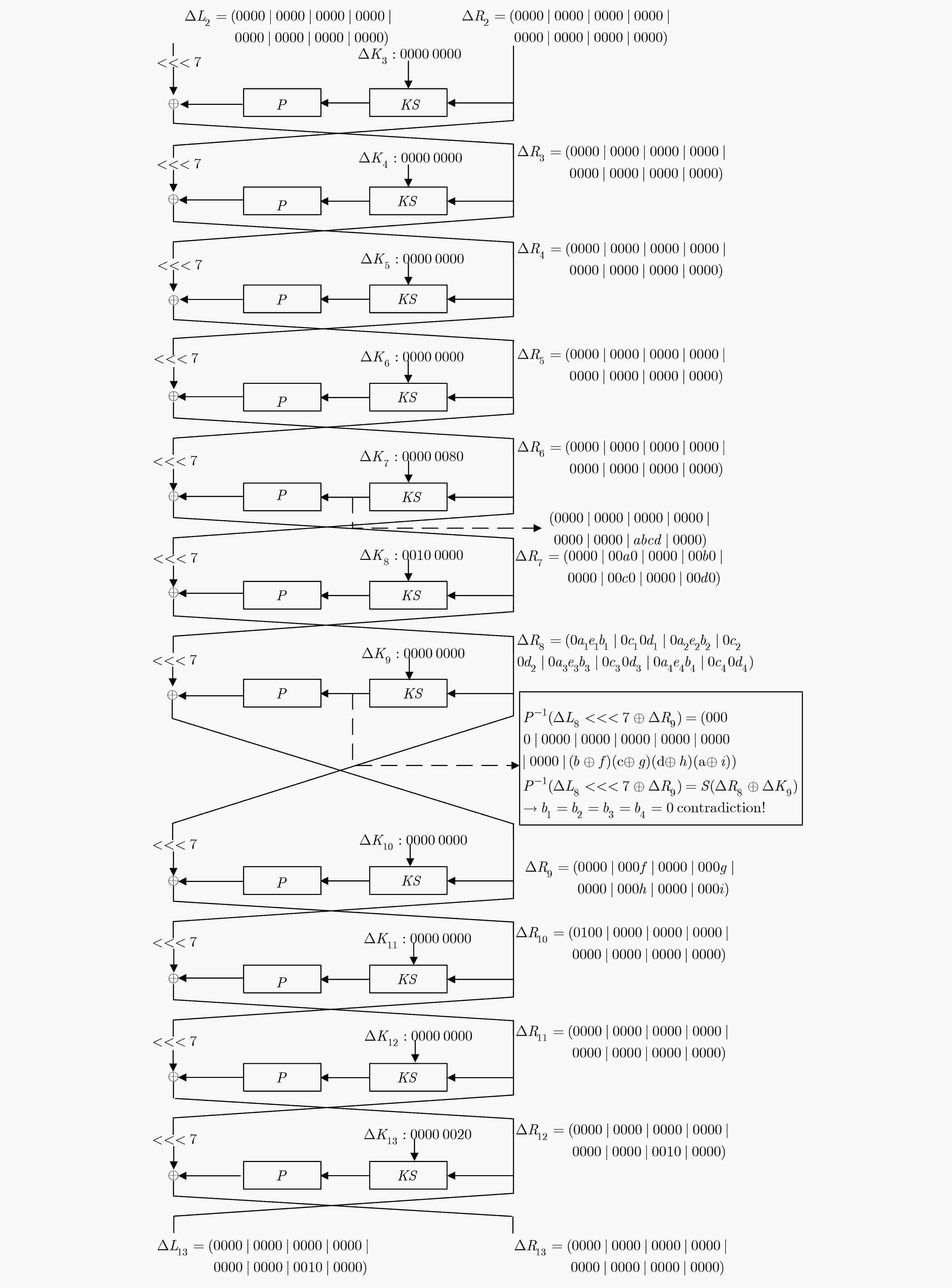
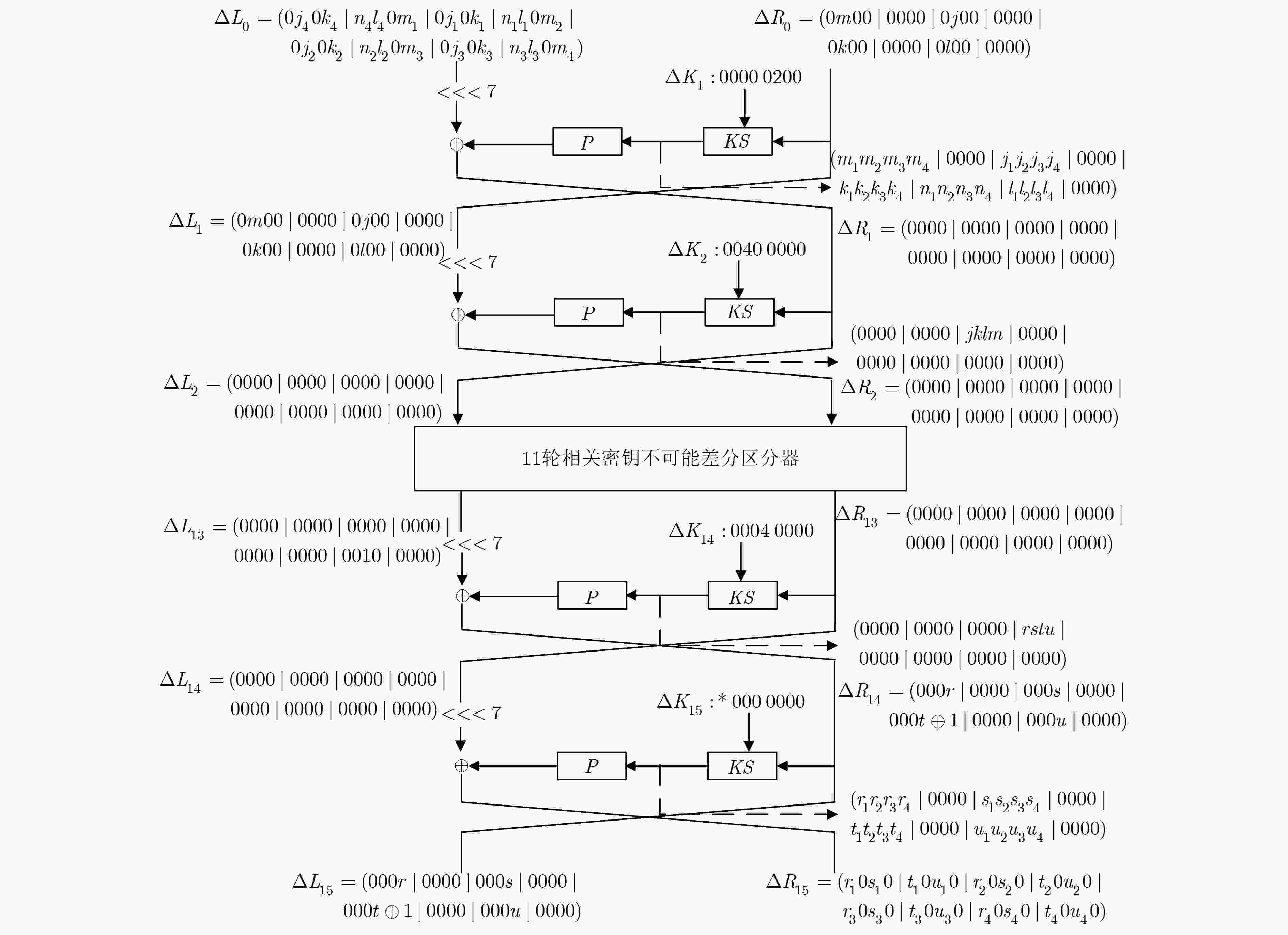
$\Delta K = (00000200000000000000)$
$\Delta {K_1}$	$0000 0200$	$\Delta {K_9}$	$0000 0000$
$\Delta {K_2}$	$0040 0000$	$\Delta {K_{10}}$	$0000 0000$
$\Delta {K_3}$	$0000 0000$	$\Delta {K_{11}}$	$0000 0000$
$\Delta {K_4}$	$0000 0000$	$\Delta {K_{12}}$	$0000 0000$
$\Delta {K_5}$	$0000 0000$	$\Delta {K_{13}}$	$0000 0020$
$\Delta {K_6}$	$0000 0000$	$\Delta {K_{14}}$	$0004 0000$
$\Delta {K_7}$	$0000 0080$	$\Delta {K_{15}}$	$*000 0000$
$\Delta {K_8}$	$0010 0000$	–	–

下载: 导出CSV 

| 显示表格

根据选取的密钥差分链，分别选择以$(00000000, 00000000)$为第3轮输入差分、以$(00000020, 00000000)$为第13轮输出差分构造相关密钥差分特征。详细的11轮ESF相关密钥不可能差分区分器如图3所示。

图 3  ESF算法的11轮相关密钥不可能差分区分器

下载: 全尺寸图片 幻灯片

分析S盒的差分分布可知，当输入差分的第1个半字节为1000的数据对进入${{{S}}_{1}}$时，该半字节的输出差分仅为1110, 0111, 1100, 1111, 1101及0110 6种可能，显然输出差分的第2位必然为非0，即图3中$b$的取值为1。则$\Delta {R_{7, 4}}$经过S盒后的输出差分${b_1}{b_2}{b_3}{b_4}$显然为非0，即${b_1}$, ${b_2}$, ${b_3}$和${b_4}$不同时为0。由${P^{ - 1}}(\Delta {L_8}\; < < < 7 \oplus \Delta {R_9}) = {P^{ - 1}}(0000|000b \oplus f|0000|$$000c \oplus g|0000|000d \oplus h|0000|000a \oplus i) =(0000|0000|$$0000|0000|0000|0000|0000|(b \oplus f)(c \oplus g)(d \oplus h)(a \oplus$$i))$可知，${P^{ - 1}}(\Delta {L_8} < < < 7 \oplus \Delta {R_9})$的第1, 3, 5和7个半字节同时为0。而$S(\Delta {R_8} \oplus \Delta {K_9}) =$$S(0{a_1}{e_1}{b_1}|0{c_1}0{d_1}|0{a_2}{e_2}{b_2}|0{c_2}0{d_2}|0{a_3}{e_3}{b_3}|0{c_3}0{d_3}|0{a_4}{e_4}$${b_4}|0{c_4}0{d_4})$，由S盒的性质可得，当输入差分非0的半字节进入S盒时，输出差分也必然非0。因为${b_1}$, ${b_2}$, ${b_3}$和${b_4}$不同时为0，所以$S(\Delta {R_8} \oplus \Delta {K_9})$的第1, 3, 5和7个半字节必然不同时为0，即$S(\Delta {R_8} \oplus$$\Delta {K_9}) \ne {P^{ - 1}}(\Delta {L_8} < < < 7 \oplus \Delta {R_9})$。因此，加密和解密的相关密钥差分特征相遇时发生矛盾，满足相关密钥不可能差分原理。所以，上述两条概率为1的相关密钥差分路径构成了11轮的相关密钥不可能差分区分器：$(00000000, 00000000 \nrightarrow (00000020,$$00000000)$。

与文献[4–6]中的8轮不可能差分区分器相比，本文构造的是11轮相关密钥不可能差分区分器，其构造方法实现了前4轮向下加密迭代过程中没有差分扩散，第13轮将输入差分与密钥差分相互抵消，从而减少差分的扩散得以提高区分器的轮数，进而在一定程度上提高攻击的轮数。与文献[8]中的11轮相关密钥差分区分器相比，在区分器轮数相同的情况下，本文构造的相关密钥不可能差分区分器可实现更高轮数的攻击，恢复更多的密钥。

3.2   15轮ESF相关密钥不可能差分分析

运用上文构造的11轮相关密钥不可能差分区分器，向前和向后分别添加2轮，可实现对15轮ESF算法的相关密钥不可能差分分析。扩展差分路径如图4所示。

图 4  ESF算法的15轮相关密钥不可能差分路径

下载: 全尺寸图片 幻灯片

基于上述15轮ESF的相关密钥不可能差分路径，下面给出具体的攻击过程：

步骤 1　数据收集。选择${2^{24}}$个明文生成一个结构，该结构包括${2^{24}} \times {2^{24}} \times {1 / 2} = {2^{47}}$个明文对，其中${L_0}$的第0, 2, 3, 4, 6, 8, 10, 11, 12, 14, 16, 18, 19, 20, 22, 24, 26, 27, 28, 30 bit和${R_0}$的第6, 14, 22, 30 bit可任意取值，剩下的比特取定值，即明文对满足输入差分为$(\Delta {L_0}, \Delta {R_0}) = (0{j_4}0{k_4}|{n_4}{l_4}0{m_1}|$$0{j_1}0{k_1}|{n_1}{l_1}0{m_2}|0{j_2}0{k_2}|{n_2}{l_2}0{m_3}|0{j_3}0{k_3}|{n_3}{l_3}0 {m_4},0m00|$$0000|0j00|0000|0k00|0000|0l00|0000)$，其中${j_i}$, ${k_i}$, ${l_i}$, ${m_i}$和${n_i}(1 \le i \le 4)$遍历各种可能。选择${2^n}$个这样的明文结构，则可以构成${2^{n + 47}}$个明文对。

步骤 2　密文筛选。将选择的明文对在$\Delta K = (00000200000000000000)$的条件下加密15轮，获得对应密文对。对密文对进行排除，只保留输出差分满足$(\Delta {L_{15}}, \Delta {R_{15}}) = (000r|0000|000s|$$0000|000t \oplus 1|0000|000u|\;0000, {r_1}0{s_1}0|{t_1}0{u_1}0|{r_2}0{s_2}0|$${t_2}0{u_2}0|{r_3}0{s_3}0|{t_3}0{u_3}0|{r_4}0{s_4}0|{t_4}0{u_4}0)$的密文对，其中$r$, $s$, $t$, $u$, ${r_j}$, ${s_j}$, ${t_j}$和${u_j}$$(1 \le j \le 4)$取所有可能的值，排除数据对后剩下的数据对个数为${2^{n + 3}}$。

步骤 3　依次猜测密钥${K_{15, 1}}$, ${K_{15, 3}}$, ${K_{15, 5}}$和${K_{15, 7}}$，共计16 bit。它们在$K$中的对应位置为${k_{33 - 30}}$, ${k_{41 - 38}}$, ${k_{49 - 46}}$和${k_{57 - 54}}$。对密文对进行局部解密一轮运算，保留输出差分满足等式${S_1}({L_{15, 1}} \oplus$${K_{15, 1}}) \oplus {S_1}({L_{15, 1}} \oplus \Delta {L_{15, 1}} \oplus {K_{15, 1}}\; \oplus \Delta {K_{15, 1}}) =\Delta R_{15, 6}^1$$||\Delta R_{15, 4}^1||\Delta R_{15, 2}^1||\Delta R_{15, 0}^1$的密文对，排除不符合要求的数据对；继续检查剩余数据对的输出差分，并排除不满足等式${S_3}({L_{15, 3}} \oplus {K_{15, 3}}) \oplus {S_3}({L_{15, 3}} \oplus$$\Delta {L_{15, 3}} \oplus {K_{15, 3}} \oplus \Delta {K_{15, 3}}) = \Delta R_{15, 6}^3||\Delta R_{15, 4}^3||\Delta R_{15, 2}^3||$$\Delta R_{15, 0}^3$的数据对。对剩余数据对检查其输出差分，排除不满足等式${S_5}({L_{15, 5}} \oplus {K_{15, 5}}) \oplus {S_5}({L_{15, 5}} \oplus \Delta {L_{15, 5}}$$\oplus {K_{15, 5}} \oplus \;\Delta {K_{15, 5}}) = \Delta R_{15, 7}^1||\Delta R_{15, 5}^1||\Delta R_{15, 3}^1||\Delta R_{15, 1}^1$的数据对；继续检查剩余数据对的输出差分，并排除不满足等式${S_7}({L_{15, 7}} \oplus {K_{15, 7}}) \oplus {S_7}({L_{15, 7}} \oplus\Delta {L_{15, 7}}$$\oplus {K_{15, 7}} \oplus \Delta {K_{15, 7}}) = \Delta R_{15, 7}^3||\Delta R_{15, 5}^3||\Delta R_{15, 3}^3||\Delta R_{15, 1}^3$的数据对。此时剩余数据对个数为${2^{n + 3}} \times {2^{ - 16}} =$${2^{n - 13}}$，该步的时间复杂度为$({2^{n + 3}} \times {2^4} + {2^{n - 1}} \times {2^8} +$${2^{n - 5}} \times {2^{12}} +{2^{n - 9}} \times {2^{16}}) \times {1 / 8} \times \;{1 / {15}} \approx {2^{n + 2.09}}$。

步骤 4　依次猜测密钥${K_{1, 1}}$, ${K_{1, 2}}$, ${K_{1, 3}}$, ${K_{1, 5}}$和${K_{1, 7}}$。它们在$K$中的对应位置为${k_{55 - 52}}$, ${k_{59 - 56}}$, ${k_{63 - 60}}$, ${k_{71 - 68}}$和${k_{79 - 76}}$，由于${k_{55 - 54}}$和${k_{57 - 56}}$在步骤3中已猜测，所以只需要猜测余下密钥，共计16 bit。对剩余数据对部分加密1轮，依次验证下列等式是否成立：${S_1}({R_{0, 1}} \oplus {K_{1, 1}}) \oplus {S_1}({R_{0, 1}} \oplus \Delta {R_{0, 1}} \oplus$${K_{1, 1}} \oplus \Delta {K_{1, 1}})=\Delta L_{0, 4}^2||\Delta L_{0, 2}^2||\Delta L_{0, 0}^2\;||\Delta L_{0, 6}^2$, ${S_2}({R_{0, 2}}$$\oplus{K_{1, 2}}) \oplus {S_2}({R_{0, 2}} \oplus \Delta {R_{0, 2}} \oplus {K_{1, 2}} \oplus \Delta {K_{1, 2}}) = \Delta L_{0, 4}^3$$||\Delta L_{0, 2}^3|| \Delta L_{0, 0}^3||\Delta L_{0, 6}^3$, ${S_3}({R_{0, 3}} \oplus {K_{1, 3}}) \oplus {S_3}(\;{R_{0, 3}} \oplus$$\Delta {R_{0, 3}} \oplus {K_{1, 3}} \!\oplus\! \Delta {K_{1, 3}}) \!=\! \Delta L_{0, 5}^0||\Delta L_{0, 3}^0||\Delta L_{0, 1}^0||\Delta L_{0, 7}^0$, ${S_5}({R_{0, 5}} \oplus {K_{1, 5}}) \oplus {S_5}({R_{0, 5}} \oplus \Delta {R_{0, 5}} \oplus {K_{1, 5}} \oplus \Delta {K_{1, 5}})$=$\Delta L_{0, 5}^2||\Delta L_{0, 3}^2||\Delta L_{0, 1}^2||\Delta L_{0, 7}^2$, ${S_7}({R_{0, 7}} \oplus{K_{1, 7}}) \oplus {S_7}$$ ({R_{0, 7}}\oplus \Delta {R_{0, 7}} \oplus {K_{1, 7}} \oplus \Delta {K_{1, 7}})=\Delta L_{0, 6}^0||\Delta L_{0, 4}^0||\Delta L_{0, 2}^0||$\Delta L_{0, 0}^0$。排除不满足以上所有等式的数据对，此时剩余数据对个数为${2^{n - 13}} \times {2^{ - 20}} = {2^{n - 33}}$，该步的时间复杂度为：$({2^{n - 13}} \times {2^{18}} + {2^{n - 17}} \times {2^{20}} +{2^{n - 21}}\times$${2^{24}} \!+\! {2^{n - 25}} \!\times\! {2^{28}} \!+\! {2^{n - 29}} \!\times\! {2^{32}}) \!\times\! {1 / 8} \times {1 / {15}}\approx {2^{n - 0.91}}$。

步骤 5　猜测密钥${K_{2, 5}}$, ${K_{1, 4}}$, ${K_{1, 5}}$, ${K_{1, 6}}$和${K_{1, 7}}$。它们在$K$中的对应位置为${k_{58 - 55}}$, ${k_{67 - 64}}$, ${k_{71 - 68}}$, ${k_{75 - 72}}$和${k_{79 - 76}}$，由于${k_{58 - 55}}$, ${k_{71 - 68}}$和${k_{79 - 76}}$在上述步骤中已被猜测，所以该步仅需要猜测余下的8 bit。对余下数据对进行局部加密两轮操作，检查其输出差分，并排除不满足等式${S_5}({R_{1, 5}} \oplus {K_{2, 5}}) \oplus {S_5}$$({R_{1, 5}} \oplus \Delta {R_{1, 5}} \oplus {K_{2, 5}} \oplus \Delta {K_{2, 5}})\; = \Delta L_{1, 5}^2||\Delta L_{1, 3}^2||\Delta L_{1, 1}^2||$$\Delta L_{1, 7}^2$的数据对，其中$R_{1, 5}^3 = S_7^2({R_{0, 7}} \oplus {K_{1, 7}}) \oplus L_{0, 4}^0$, $R_{1, 5}^2 = S_6^2({R_{0, 6}} \oplus {K_{1, 6}}) \oplus L_{0, 3}^3$, $R_{1, 5}^1 = S_5^2({R_{0, 5}} \oplus {K_{1, 5}})$$\oplus L_{0, 3}^2$, $R_{1, 5}^0 = S_4^2({R_{0, 4}} \oplus {K_{1, 4}}) \oplus L_{0, 3}^1$。此时剩余数据对个数为${2^{n - 33}} \times {2^{ - 4}} = {2^{n - 37}}$，该步的时间复杂度为：${2^{n - 33}} \times {2^{40}} \!\times\! {2 / 8} \!\times\! {1 / {15}} \approx {2^{n + 1.09}}$。

步骤 6　猜测${R_{13, 4}}$的值，总共${2^4}$种可能。进行局部解密两轮，保留满足$F(\Delta {R_{13, 4}} \oplus \Delta {K_{14, 4}}) \oplus$$(\Delta L_{15, 7}^0||\;\Delta L_{15, 5}^0||\Delta L_{15, 3}^0||\Delta L_{15, 1}^0) = (0010)$的数据对。由${{\rm{S}}_{4}}$的差分分布表知，满足第14轮输出要求的概率为${1 / 6}$，则此步之后剩余数据对个数为${2^{n - 37}} \times$${2^4} \times {1 / 6} \approx {2^{n - 35.58}}$，该步的时间复杂度为：${2^{n - 37}} \times$${2^4} \times {2^{40}} \times {1 / 8} \times {1 / {15}} \approx {2^{n + 0.09}}$。选择${2^{37.5}}$个明文结构，即取$n = 37.5$，经上述步骤过滤后，还有剩余的数据对，表明以上猜测满足了该相关密钥不可能差分路径，从而是错误密钥，需将其剔除并重新猜测密钥。因此该攻击的时间复杂度为：${2^{n + 2.09}} +$${2^{n - 0.91}} + {2^{n + 1.09}} + {2^{n + 0.09}} \approx {2^{n + 3}} = {2^{40.5}}$次15轮加密运算，明文量为：${2^{37.5 + 24}} = {2^{61.5}}$个选择明文。

综上，本文采用相关密钥不可能差分分析15轮ESF的时间复杂度约为${2^{40.5}}$次15轮加密操作，数据复杂度为${2^{61.5}}$个选择明文，总共恢复40 bit密钥。

3.3   结果对比

目前对ESF的攻击最常用的方法为不可能差分分析，还有少量评估ESF在差分故障攻击与相关密钥差分攻击下的安全性的文献。本文评估了ESF抵抗相关密钥不可能差分分析能力，与现有攻击结果相比，首次将攻击轮数提高到15轮，比目前最好结果提高两轮，并且攻击时间复杂度大幅度降低，恢复的密钥比特数也具有较大优势，均优于文献[4–6,8]的结果，具体攻击结果对比如表3所示。

表 3  ESF算法的攻击结果比较

攻击方法	轮数	时间复杂度	数据复杂度	文献
不可能差分	11	${2^{75.5}}$	${2^{59}}$	[4]
不可能差分	11	${2^{32}}$	${2^{53}}$	[5]
不可能差分	12	${2^{60.43}}$	${2^{53}}$	[6]
相关密钥差分	13	${2^{66}}$	${2^{47}}$	[8]
相关密钥不可能差分	15	${2^{40.5}}$	${2^{61.5}}$	本文

下载: 导出CSV 

| 显示表格

4.   结束语

本文通过分析ESF的密钥扩展算法的弱点、S盒的差分性质以及相关密钥不可能差分分析方法的优点，以减少活跃S盒的数量来获取更长的差分链为基本思想，选定特殊的密钥和明文差分使其互相抵消，构造出11轮相关密钥不可能差分区分器，并将其前后各添加两轮，对ESF进行了15轮相关密钥不可能差分攻击，其攻击的时间复杂度远低于穷举攻击的复杂度，攻击效果与现有结果相比也具有较大优势。将多种分析方法相结合可以充分利用各种分析方法的优势，取长补短，有利于攻击更高轮数的算法，获得更加理想的攻击结果。在未来的工作中，可考虑对路径搜索算法加以优化，寻找更好的相关密钥不可能差分路径来改善目前已有的结果，或将相关密钥不可能差分分析与其他分析方法相结合，以期完成对更高轮数的ESF算法分析。