An Accurate Wideband Beampattern Synthesis Method Based on the Space-frequency Structure and the Space-time Structure Conversion
-
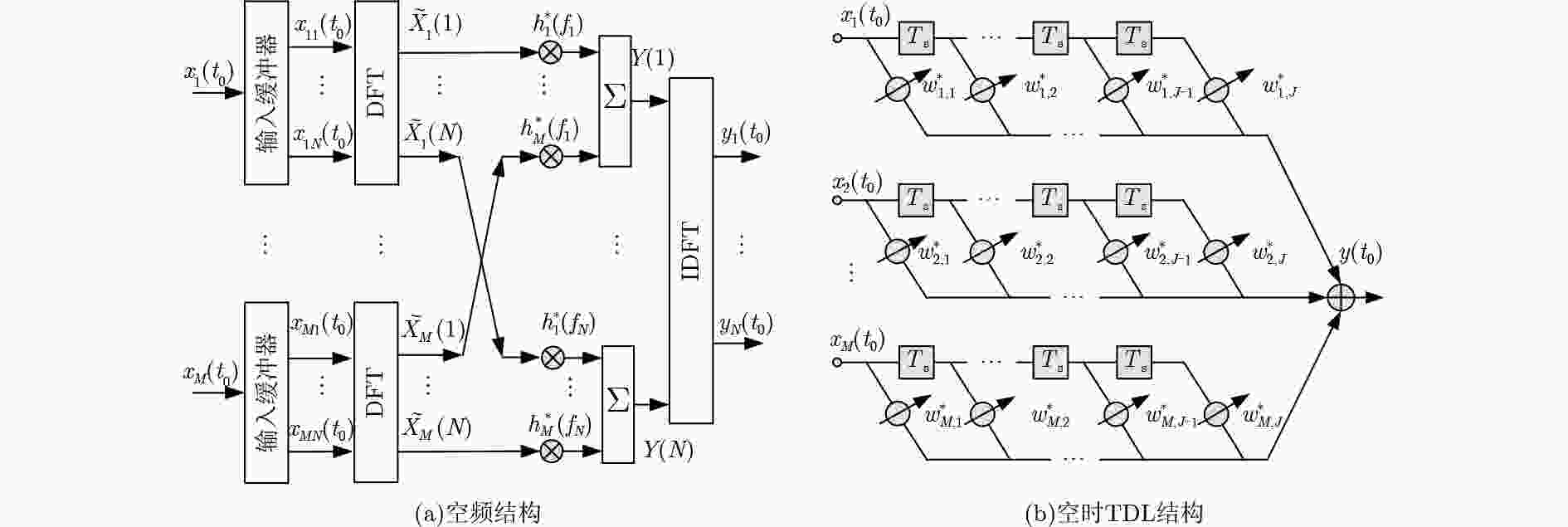
摘要:
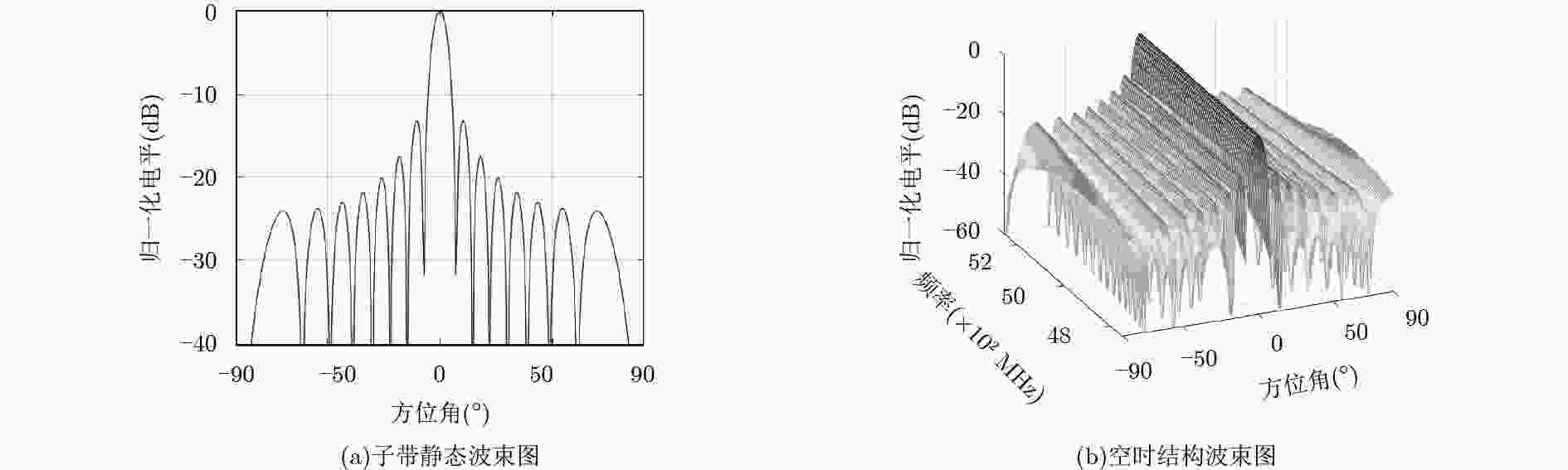
该文提出一种空时结构下的精确宽带波束赋形算法。在空频结构下,对各子带权值进行波束赋形优化。根据权值在满足共轭对称条件下,阵列幅度响应可以转换为线性函数这一原理,将波束赋形转换为凸优化问题。利用内点法得到最优权值后,通过空频结构与空时结构之间的权值转换关系,得到空时结构下的波束权值。该算法能够对宽带波束图进行精确地赋形,同时保证在期望方向上阵列响应具有线性相位特性。仿真结果验证了算法的有效性。
Abstract:An accurate wideband beampattern synthesis method based on the space-time structure is proposed. Making use of the property that the magnitude response can be translated into linear function under the condition of conjugate symmetric weights, the beampattern synthesis problem is transformed into the convex optimization problem. The weights of space-time structure can be obtained by utilizing the principle of relationship between the two structures, after the weights of space-frequency structure is calculated by the interior point method. The proposed method can realize the wideband beampattern synthesis accurately, meanwhile ensuring the linear phase characteristic of the array response. Simulation results demonstrate the effectiveness of the proposed method.
-
表 1 3种方法的计算量比较
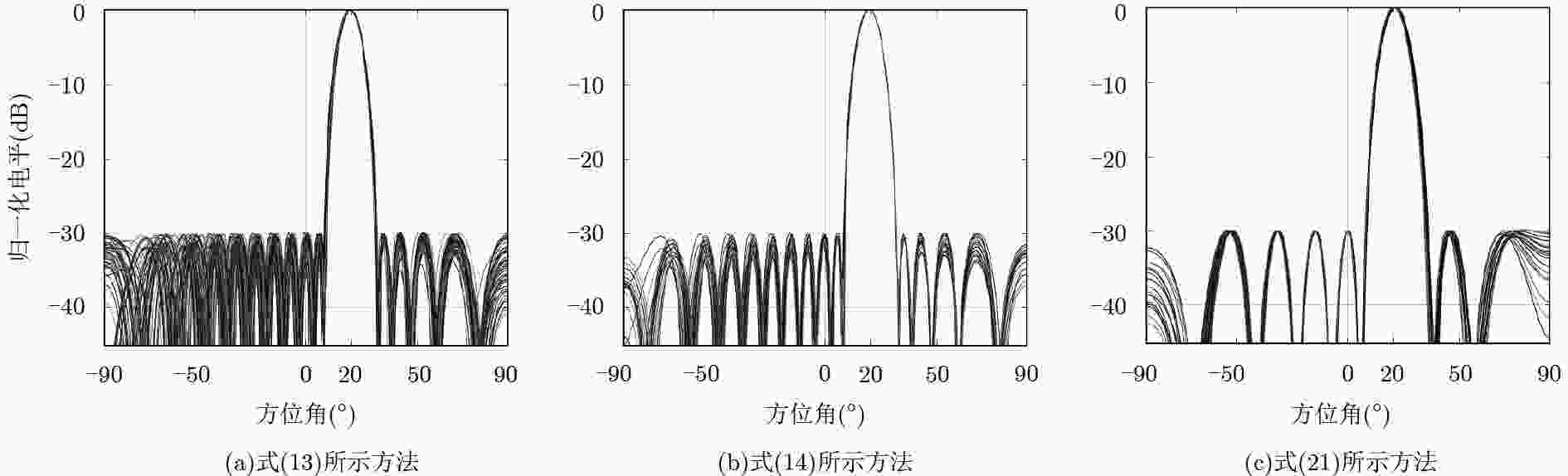
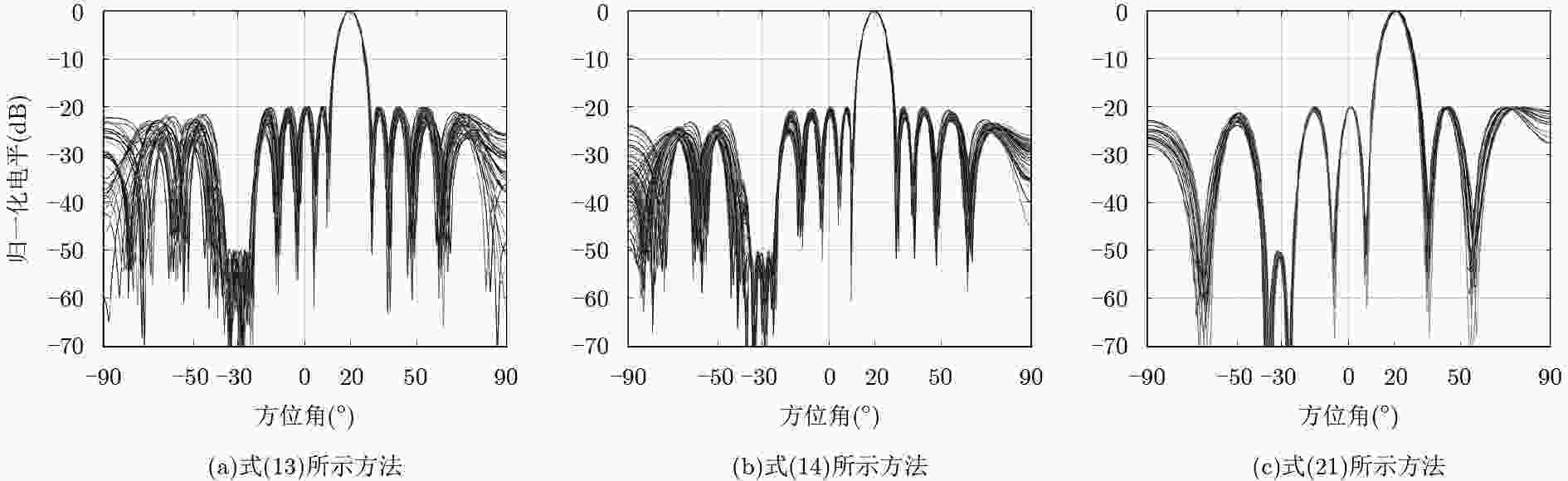
方法 迭代次数 每次迭代的运算量 式(13) $O\left(\sqrt {{K_4}(2{K_1} + {K_2} + {K_3}) + 2} \right)$ $O\left\{ (MN)^2[{K_4}(6{K_1} + 3{K_2}{+ 3}{K_3}) + 2{K_4} + 1]\right\} $ 式(14) $O\left(\sqrt {2{K_1} + {K_4}({K_2} + {K_3}) + 2} \right)$ $O\left\{ {(MN)^2}[6{K_1} + 3{K_4}({K_2} + {K_3}) + MN{\rm{ + }}3]\right\} $ 式(21) $O\left(\sqrt {2N} \right)$ $O\left\{ {(M/2)^2}[N(4{K_1} + 2{K_2} + 2{K_3}) + MN + 3N]\right\} $ -
KNIGHT W C, PRIDHAM R G, and KAY S M. Digital signal processing for sonar[J]. Proceedings of the IEEE, 1981, 69(11): 1451–1506. doi: 10.1109/PROC.1981.12186 GINI F, FARINA A, and GERCO M. Selected list of references on radar signal processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 329–359. doi: 10.1109/7.913696 GIANNAKIS G B. Highlights of signal processing for communications[J]. IEEE Signal Processing Magazine, 1999, 16(2): 14–50. doi: 10.1109/MSP.1999.752038 ELLINGSON S W and HAMPSON G A. Aubspace-tracking approach to interference nulling for phased array-based radio telescopes[J]. IEEE Transactions on Antennas and Propagation, 2002, 50(1): 25–30. doi: 10.1109/8.992558 KARAMAN M, ATALAR A, and KOYMEN H. VLSI circuits for adaptive digital beamforming in ultrasound imaging[J]. IEEE Transactions on Medical Imaging, 1993, 12(4): 711–720. doi: 10.1109/42.251122 FROST O L. An algorithm for linearly constrained adaptive array processing[J]. Proceedings of the IEEE, 1972, 60(8): 926–935. doi: 10.1109/PROC.1972.8817 DENTINO M, MCCOOL J, and WIDROW B. Adaptive filtering in the frequency domain[J]. Proceedings of the IEEE, 1978, 66(12): 1658–1659. doi: 10.1109/PROC.1978.11177 HAMID U, QAMAR R A, and WAQAS K. Performance compariason of time-domain and frequency-domain beamforming techniques for sensor array processing[C]. Proceedings of 2014 11th International Bhurban Conference on Applied Science & Technology, Islamabad, Pakistan, 2014: 379–385. doi: 10.1109/IBCAST.2014.6778172. GODARA L C and JAHROMI M R S. Limitations and capabilities of frequency domain broadband constrained beamforming schemes[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2386–2395. doi: 10.1109/78.782182 COMPTON R T. The relationship between tapped delay-line and FFT processing in adaptive arrays[J]. IEEE Transactions on Antennas and Propagation, 1988, 36(1): 15–26. doi: 10.1109/8.1070 GODARA L C. Application of the fast fourier transform to broadband beamforming[J]. The Journal of the Acoustical Society of America, 1995, 98(1): 230–240. doi: 10.1121/1.413765 王力, 何丙发, 孙庆锋. 一种阵列天线快速波束赋形方法[J]. 现代雷达, 2016, 38(8): 70–74. doi: 10.16592/j.cnki.1004-7859.2016.08.016WANG Li, HE Bingfa, and SUN Qingfeng. Synthesis of the shaped-beam array antennas using a fast algorithm[J]. Modern Radar, 2016, 38(8): 70–74. doi: 10.16592/j.cnki.1004-7859.2016.08.016 郑占旗, 阎跃鹏, 张立军, 等. 增加副瓣抑制机制的阵列天线波束赋形遗传算法研究[J]. 电子与信息学报, 2017, 39(3): 690–696. doi: 10.11999/JEIT160466ZHENG Zhanqi, YAN Yuepeng, ZHANG Lijun, et al. Research on genetic algorithm of antenna arrays beam shaping with side lobe suppression[J]. Journal of Electronics &Information Technology, 2017, 39(3): 690–696. doi: 10.11999/JEIT160466 LIANG Junli, FAN Xuhui, FAN Wen, et al. Phase-only pattern synthesis for linear antenna arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 3232–3235. doi: 10.1109/LAWP.2017.2771380 陈俊杰, 金荣洪, 耿军平. 一种基于牛顿下山法的宽带阵列方向图综合算法[J]. 上海交通大学学报, 2007, 41(8): 1366–1369. doi: 10.3321/j.issn:1006-2467.2007.08.033CHEN Junjie, JIN Ronghong, and GENG Junping. A wideband array beam pattern synthesis algorithm based on newton downhill method[J]. Journal of Shanghai Jiaotong University, 2007, 41(8): 1366–1369. doi: 10.3321/j.issn:1006-2467.2007.08.033 陈明建, 罗景青. 基于叠加变加权最小二乘的宽带波束赋形方法[J]. 宇航学报, 2012, 33(6): 796–801. doi: 10.3873/j.issn.1000-1328.2012.06.016CHEN Mingjian and LUO Jingqing. A method for broadband shoped beam based on iterative variably-weighted least squares[J]. Journal of Astronautics, 2012, 33(6): 796–801. doi: 10.3873/j.issn.1000-1328.2012.06.016 贾深惠, 赵拥军, 陈沛, 等. 基于二阶锥规划的共形阵列宽带方向图综合[J]. 信息工程大学学报, 2016, 17(4): 437–442. doi: 10.3969/j.issn.1671-0673.2016.04.011JIA Shenhui, ZHAO Yongjun, CHEN Pei, et al. Conformal array beamforming for broadband signals based on second order cone programming[J]. Journal of Information Engineering University, 2016, 17(4): 437–442. doi: 10.3969/j.issn.1671-0673.2016.04.011 刘子龙, 丁淑娟, 孙广俊, 等. 基于二阶锥规划的宽带波束形成器设计[J]. 计算机工程与应用, 2013, 49(5): 195–199. doi: 10.3778/j.issn.1002-8331.1107-0521LIU Zilong, DING Shujuan, SUN Guangjun, et al. Design of broadband beamformer based on second-order cone programming[J]. Computer Engineering and Application, 2013, 49(5): 195–199. doi: 10.3778/j.issn.1002-8331.1107-0521 YAN Shefeng, MA Yuanliang, and HOU Chaohuan. Optimal array pattern synthesis for broadband arrays[J]. Journal of the Acoustical of America, 2007, 122(5): 2686–2696. doi: 10.1121/1.2785037 DUAN Huiping, NG B P, SEE C M S, et al. Application of the SRV constraint in broadband pattern synthesis[J]. Signal Processing, 2008, 88(4): 1035–1045. doi: 10.1016/j.sigpro.2007.11.001 ZHANG Tongtong and SER W. Robust beampattern synthesis for antenna arrays with mutual coupling effect[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(8): 2889–2895. doi: 10.1109/TAP.2011.2152329 BOYD S and VANDENBERGHE L. Convex Optimization[M]. New York, USA: Cambridge University Press, 2004: 127–189. 虞泓波, 冯大政, 解虎. 相位响应固定幅度响应约束的稳健波束形成方法[J]. 电子与信息学报, 2015, 37(7): 1688–1694. doi: 10.11999/JEIT141513YU Hongbo, FENG Dazheng, and XIE Hu. Robust beamforming with phase response fixed and magnitude response constraint[J]. Journal of Electronics &Information Technology, 2015, 37(7): 1688–1694. doi: 10.11999/JEIT141513 LIAO Bin, TSUI K M, and CHAN Shingchow. Robust beamforming with magnitude response constraints using iterative second-order cone programming[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(9): 3477–3482. doi: 10.1109/TAP.2011.2161445 XU Dingjie, HE Rui, and SHEN Feng. Robust beamforming with magnitude response constraints and conjugate symmetric constraint[J]. IEEE Communication Letters, 2013, 17(3): 561–564. doi: 10.1109/LCOMM.2013.011513.122688 ZHU Liangyu, SER W, ER M H, et al. Robust adaptive beamformers based on worst-case optimization and constraints on magnitude response[J]. IEEE Transaction on Signal Processing, 2009, 57(7): 2615–2628. doi: 10.1109/TSP.2009.2017004 -





 下载:
下载:
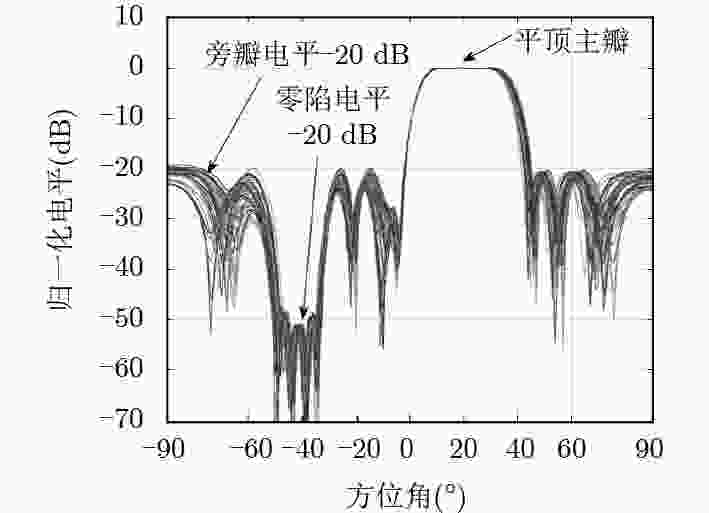


 下载:
下载:
