An Adaptive Consistent Iterative Hard Thresholding Alogorith for Audio Declipping
-
摘要:
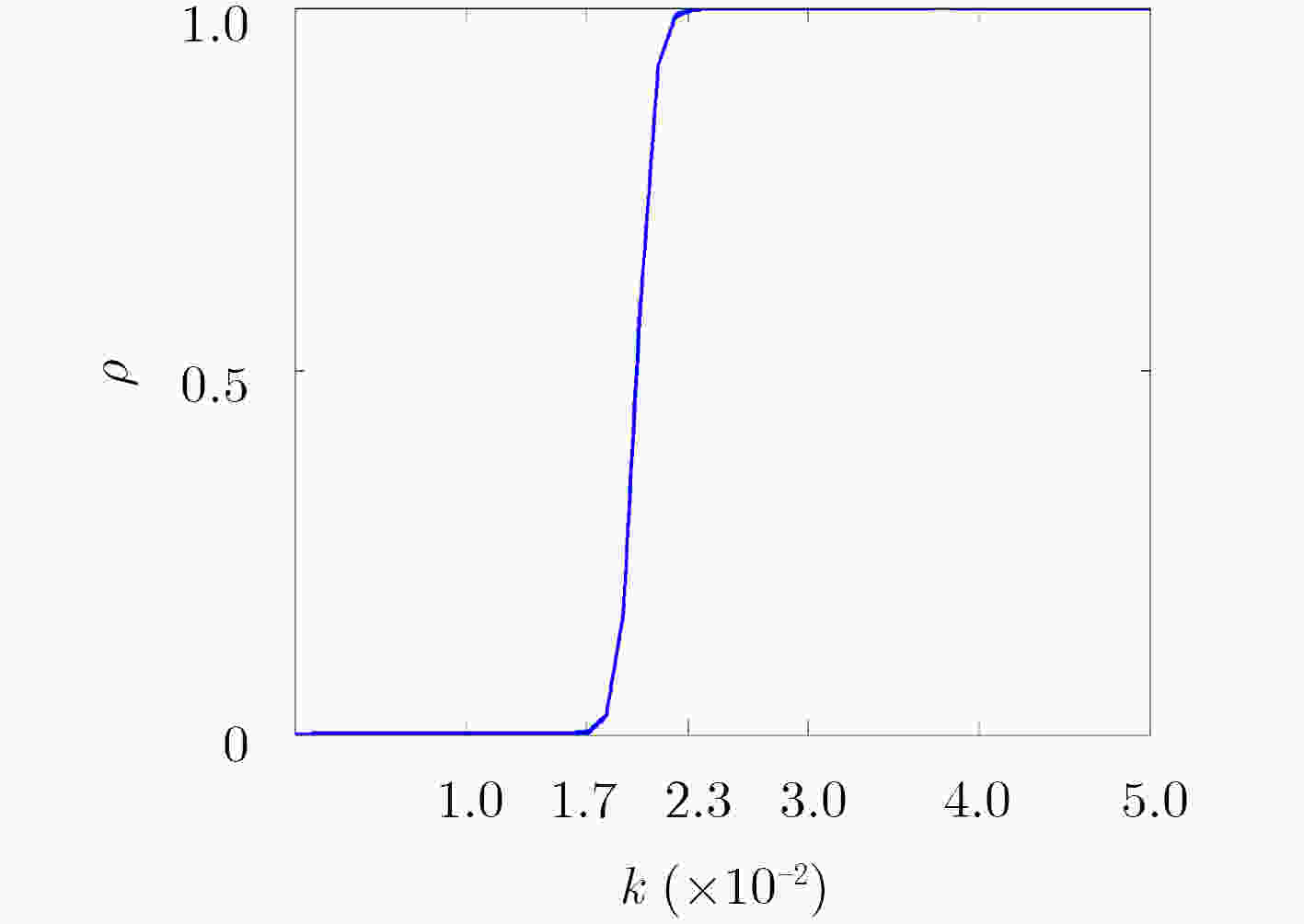
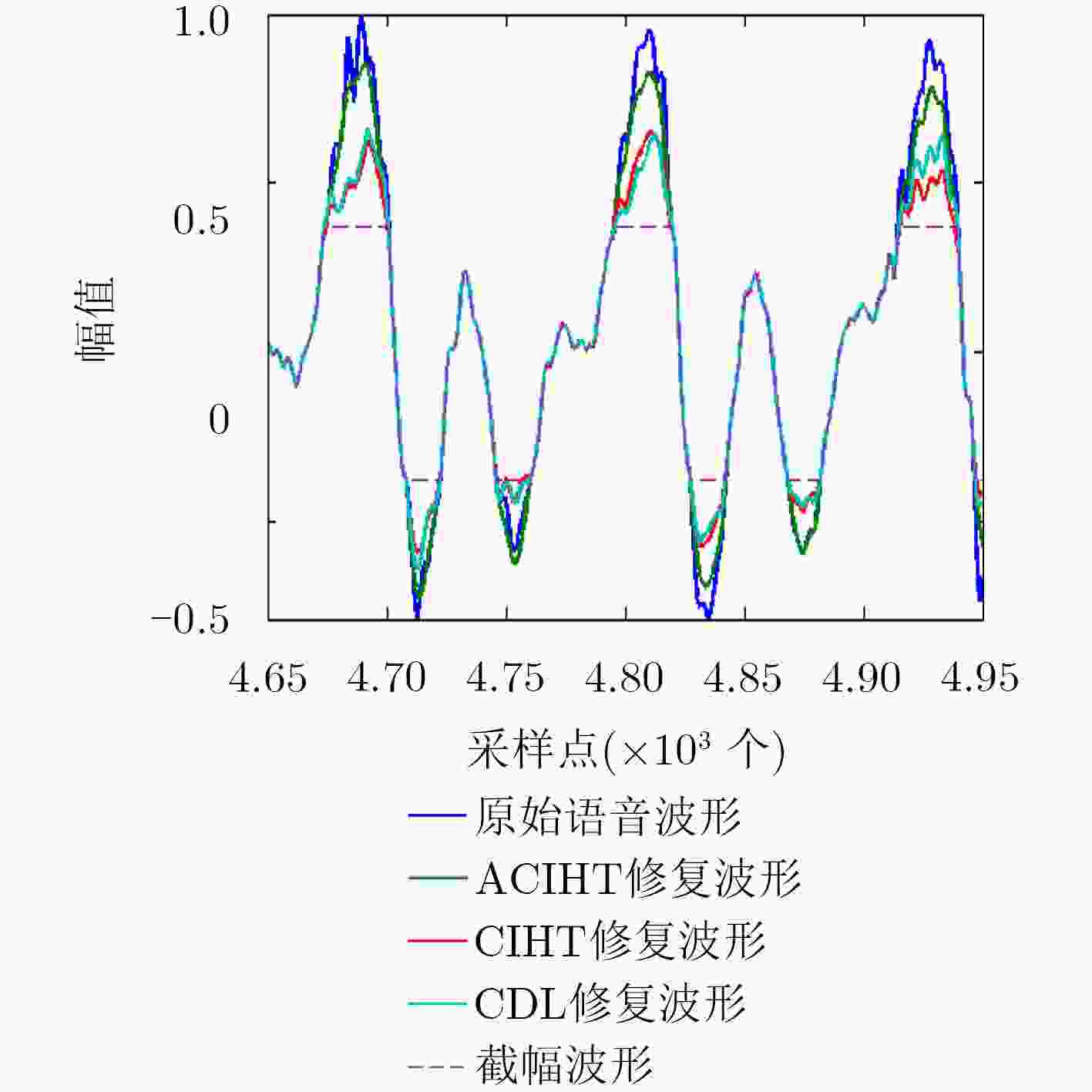
一致迭代硬阈值(CIHT)算法在处理音频截幅失真中具有较好的性能。但是,在截幅程度较大时音频截幅修复的性能会下降。因此,该文提出一种基于自适应门限的改进算法。该算法自动估计音频信号截幅程度,根据估计的截幅程度信息,自适应调整算法中的截幅程度因子。与近年来提出的CIHT算法和一致字典学习算法(CDL)相比,该文所提算法能更好地重建音频信号,特别在音频信号截幅失真严重的情况。该算法的运算复杂度与CIHT相近,与CDL相比,拥有更快的运行速度,有利于实时实现。
Abstract:Audio clipping distortion can be solved by the Consistent Iterative Hard Thresholding (CIHT) algorithm, but the performance of restoration will decrease when the clipping degree is large, so, an algorithm based on adaptive threshold is proposed. The method estimates automatically the clipping degree, and the factor of the clipping degree is adjusted in the algorithm according to the degree of clipping. Compared with the CIHT algorithm and the Consistent Dictionary Learning (CDL) algorithm, the performance of restoration by the proposed algorithm is much better than the other two, especially in the case of severe clipping distortion. Compared with CDL, the computational complexity of the proposed algorithm is low like CIHT, compared with CDL, it has faster processing speed, which is beneficial to the practicality of the algorithm.
-
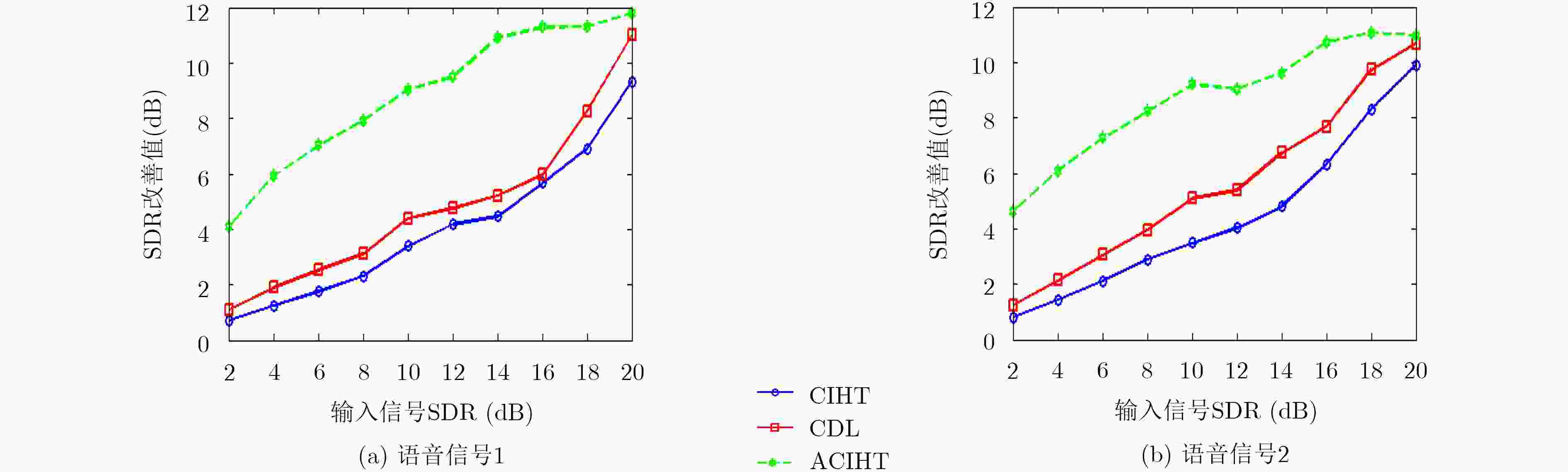
表 1 截幅语音信号1修复前后PESQ得分比较
输入语音
SDR (dB)截幅语音 CIHT算法
修复后CDL算法
修复后ACIHT算法
修复后2 1.8838 2.0877 2.1201 2.2400 4 2.2041 2.4411 2.4860 2.6039 6 2.3451 2.6239 2.6247 2.8551 8 2.5084 2.7974 2.7608 3.1258 10 2.6576 3.0501 3.0715 3.2847 12 2.7951 3.2538 3.3020 3.6657 14 2.9858 3.4915 3.5057 3.8716 16 3.1098 3.6881 3.6223 4.1016 18 3.2984 3.8203 3.7167 4.2174 20 3.4128 4.1934 4.2224 4.2440 表 2 截幅语音信号2修复前后PESQ得分比较
输入语音
SDR (dB)截幅语音 CIHT算法
修复后CDL算法
修复后ACIHT算法
修复后2 1.7080 1.8980 1.9802 2.2026 4 1.9977 2.3065 2.3451 2.5566 6 2.2115 2.6041 2.6537 2.7818 8 2.3900 2.8904 2.9176 3.0617 10 2.5946 3.1397 3.2116 3.3242 12 2.7625 3.4662 3.4546 3.4784 14 2.9359 3.7844 3.8324 3.9217 16 3.2481 3.9820 4.0386 4.0463 18 3.3362 4.2150 4.1375 4.3005 20 3.4004 4.3186 4.2845 4.3500 -
JANSSEN A, VELDHUIS R, and VRIES L. Adaptive interpolation of discrete-time signals that can be modeled as autoregressive processes[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(2): 317–330 doi: 10.1109/TASSP.1986.1164824 ABEL J S and ABEL J S. Restoring a clipped signal[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Toronto, Canada, 1991, 3: 1745–1748. SIMON J G, PATRICK J, and WILLIAM N W. Statistical model-based approaches to audio restoration and analysis[J]. Journal of New Music Research, 2001, 30(4): 323–338 doi: 10.1076/jnmr.30.4.323.7489 ADLER A, EMIYA V, and JAFARI M G. Audio Inpainting[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2012, 20(3): 922–932 doi: 10.1109/TASL.2011.2168211 ADLER A, EMIYA V, and JAFARI M G. A constrained matching pursuit approach to audio declipping[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Prague, Czech Republic, 2011: 329–332. DEFRAENE B, MANSOUR N, and HERTOGH S D. Declipping of audio signals using perceptual compressed sensing[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2013, 21(12): 2627–2637 doi: 10.1109/TASL.2013.2281570 FOUCART S and NEEDHAM T. Sparse recovery from saturated measurements[J]. Information and Inference: A Journal of the IMA, 2017, 6(2): 196–212 doi: 10.1093/imaiai/iaw020 OZEROV A, BILEN C, and PEREZ P. Multichannel audio declipping[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Shanghai, China, 2016: 659–663. KAI S, KOWALSKI M, and DORFLER M. Audio declipping with social sparsity[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Florence, Italy, 2014: 1577–1581. KITIC S, JACQUES L, and MADHU N. Consistent iterative hard thresholding for signal declipping[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Vancouver, Canada, 2013: 5939–5943. RENCKER L, BACH F, WANG Wenwu, et al. Consistent dictionary learning for signal declipping[C]. International Conference on Latent Variable Analysis and Signal Separation, Guildford, UK, 2018: 446–455. LECUE G and FOUCART S. An IHT algorithm for sparse recovery from sub-exponential measurements[J]. IEEE Signal Processing Letters, 2017, 24(3): 1280–1283 doi: 10.1109/LSP.2017.2721500 HINES A, SKOGLUND J, and KOKARAM A. Robustness of speech quality metrics to background noise and network degradations: Comparing ViSQOL, PESQ and POLQA[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Vancouver, Canada, 2013: 3697–3701. 何孝月. 基于EPESQ的VoIP语音质量评估的研究与实现[D]. [硕士论文], 中南大学, 2008.HE Xiaoyue. Speech Quality Evaluation of VoIP Based on EPESQ[D]. [Master dissertation], Central South University, 2008. -





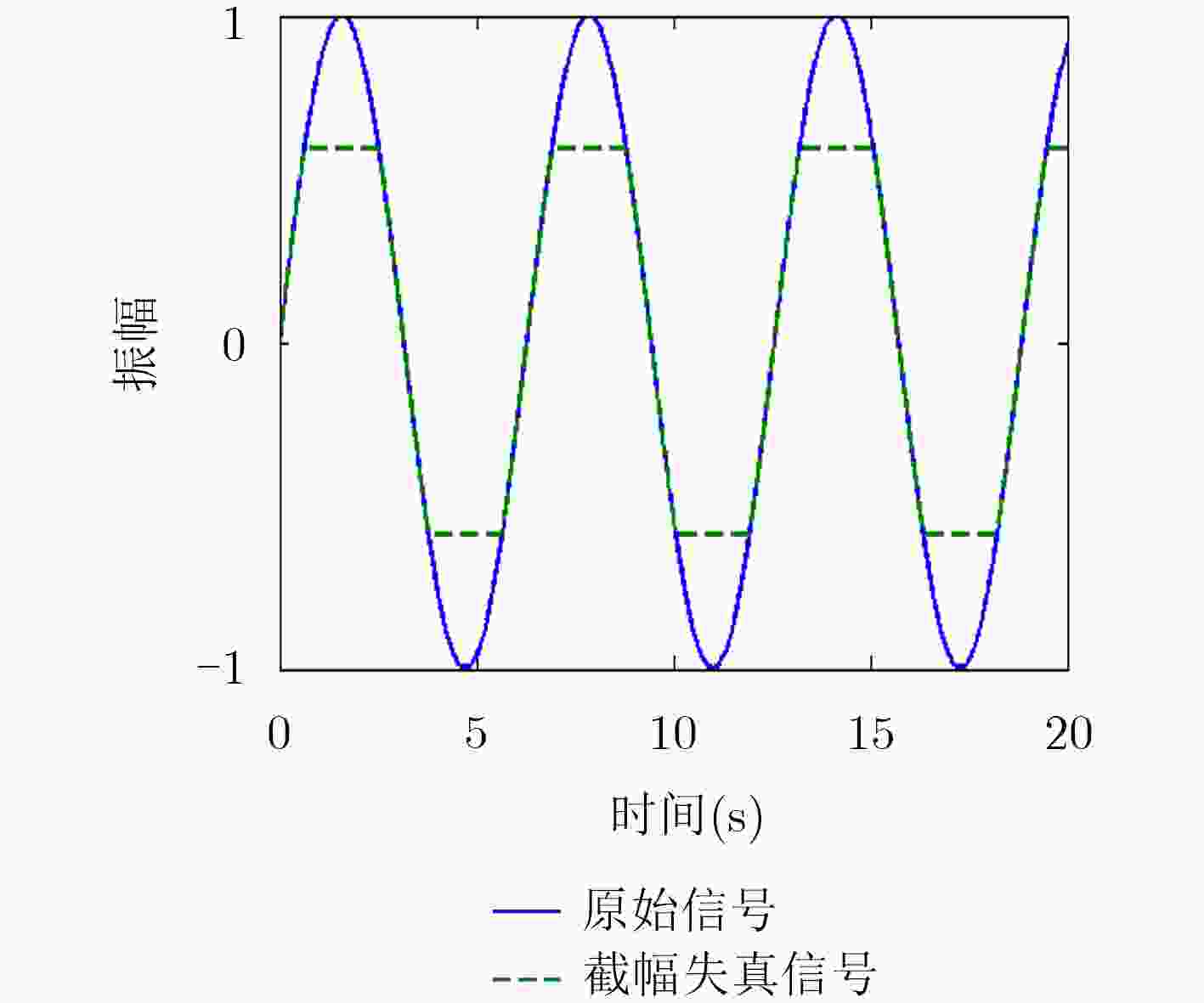
 下载:
下载:
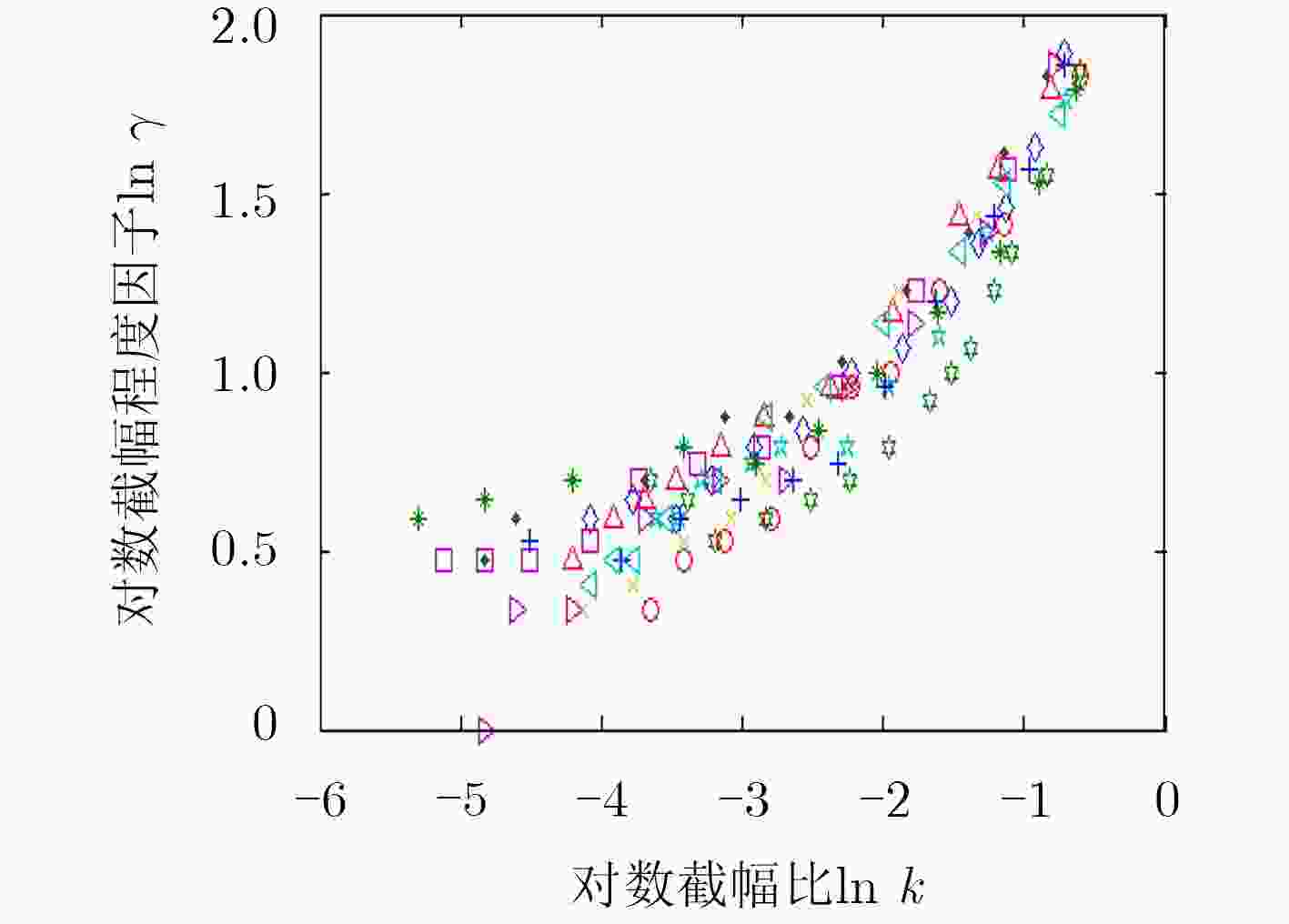
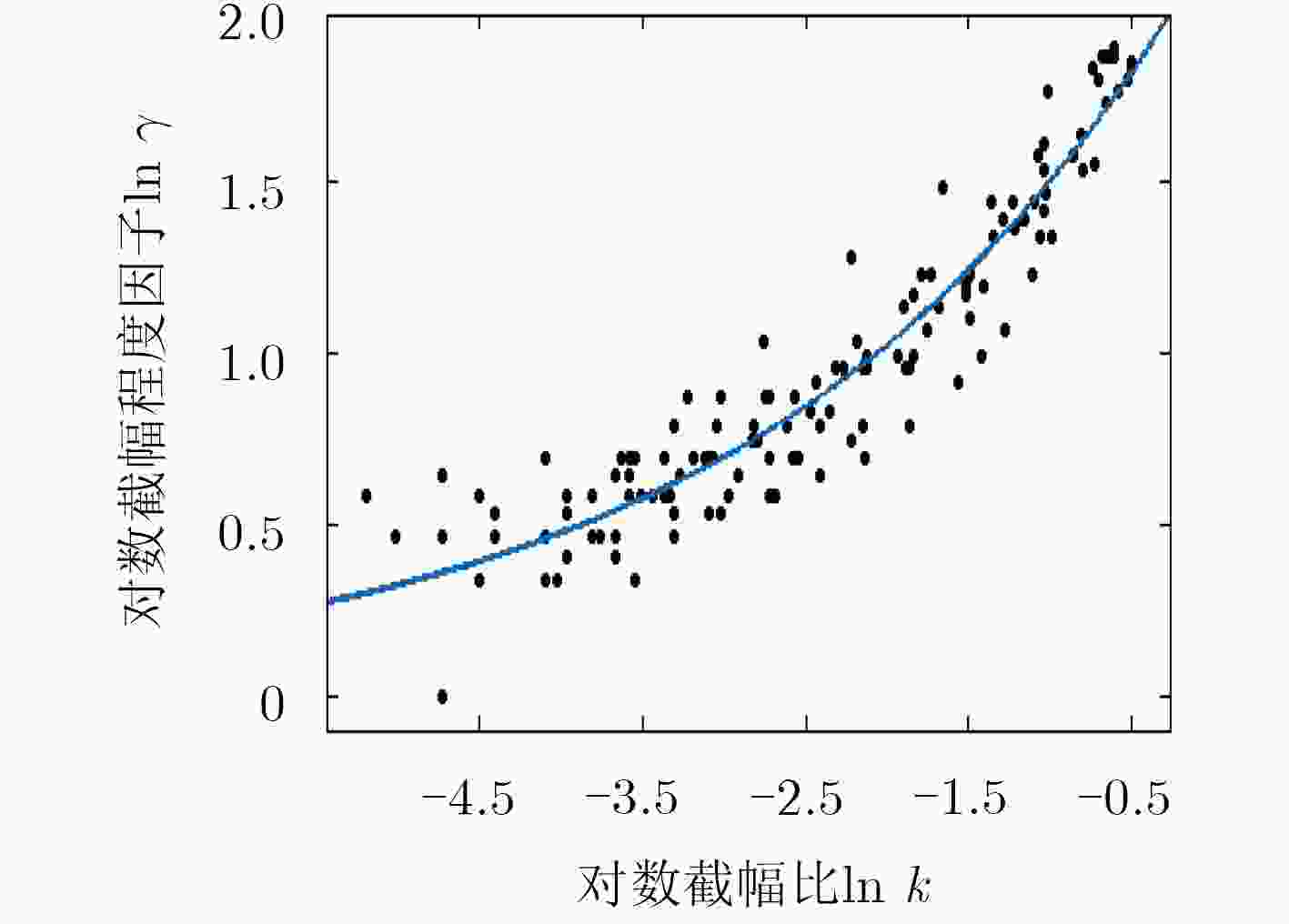
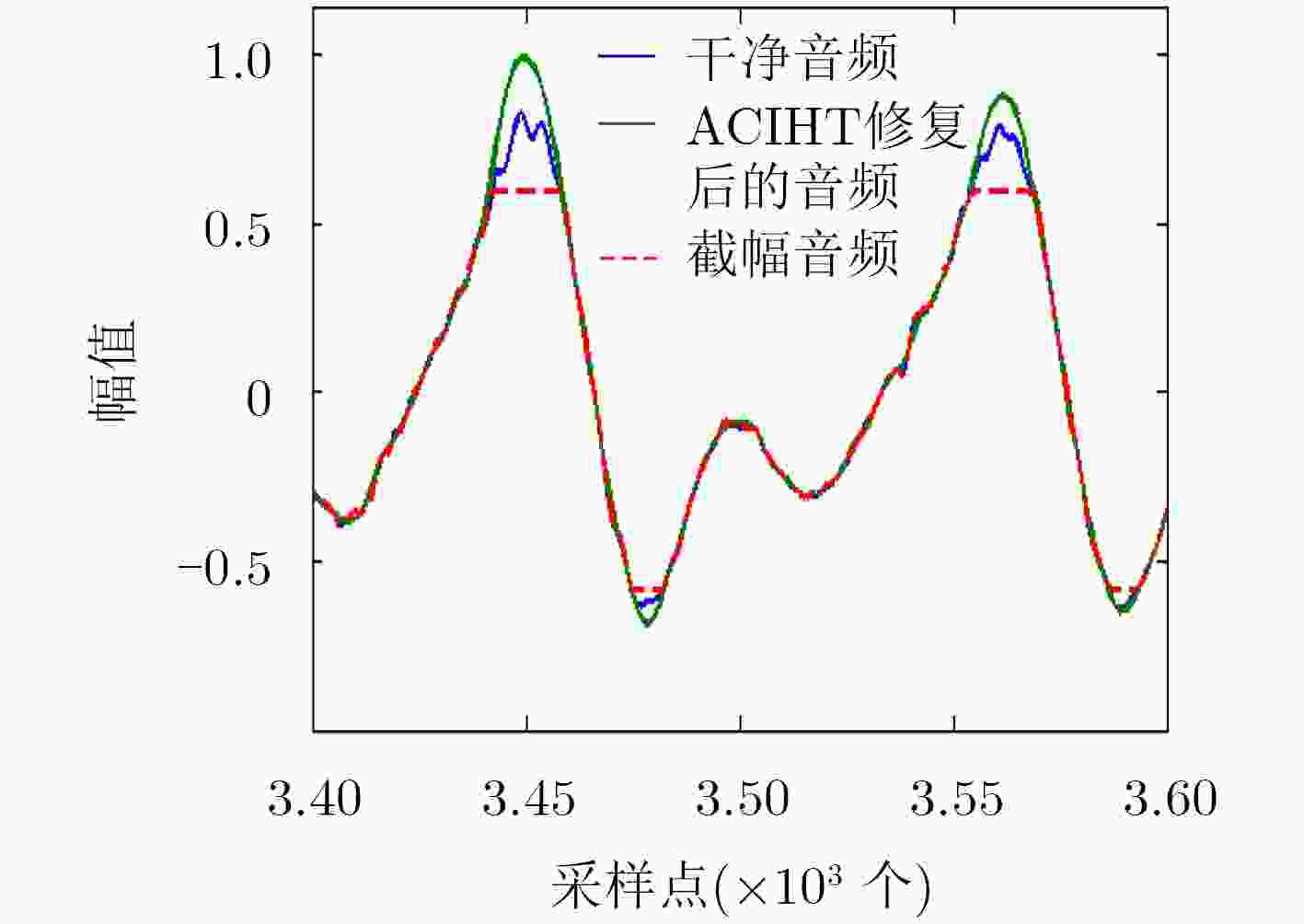




 下载:
下载:
