Direction Finding for Electromagnetic Radiation Source Using Ultra-short Baseline Array
-
摘要:
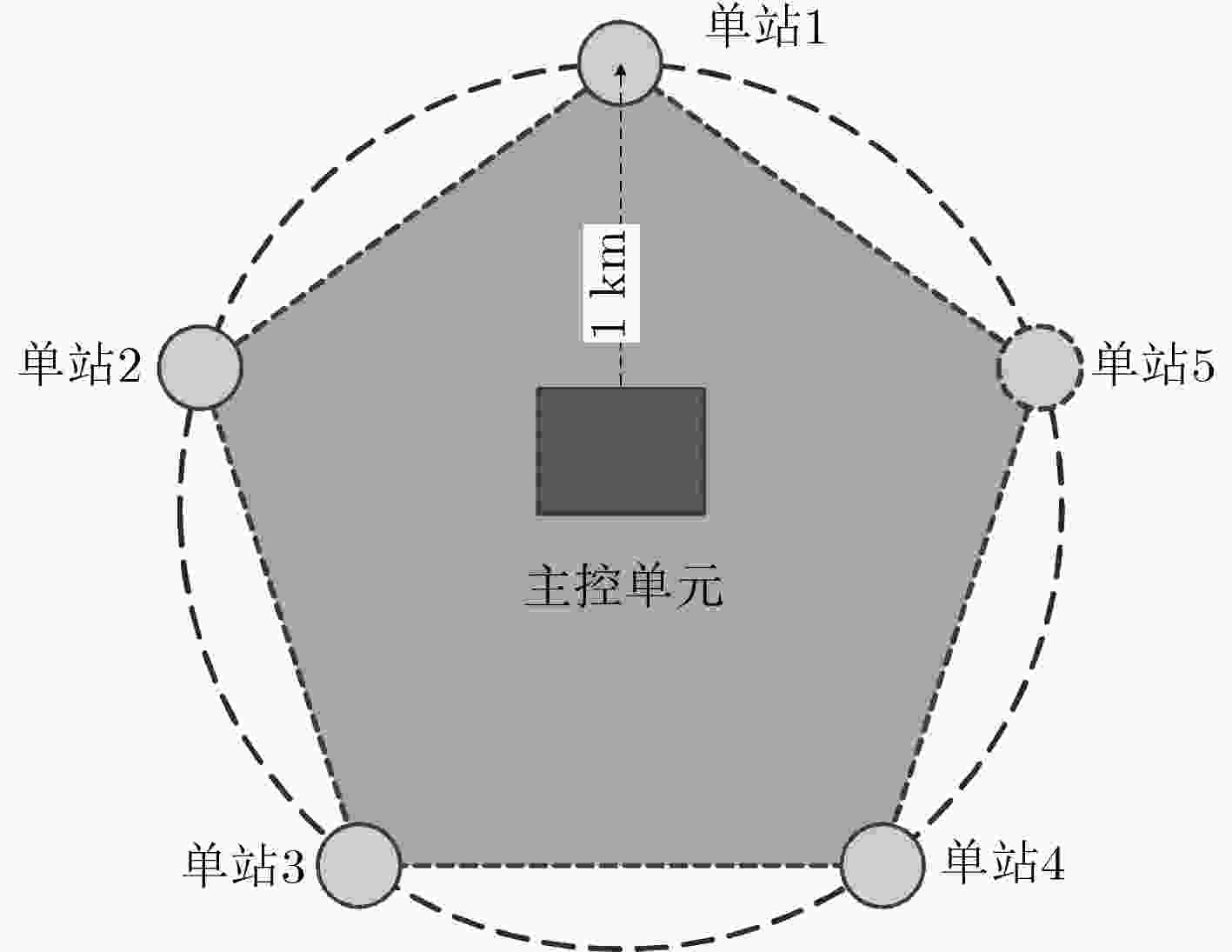
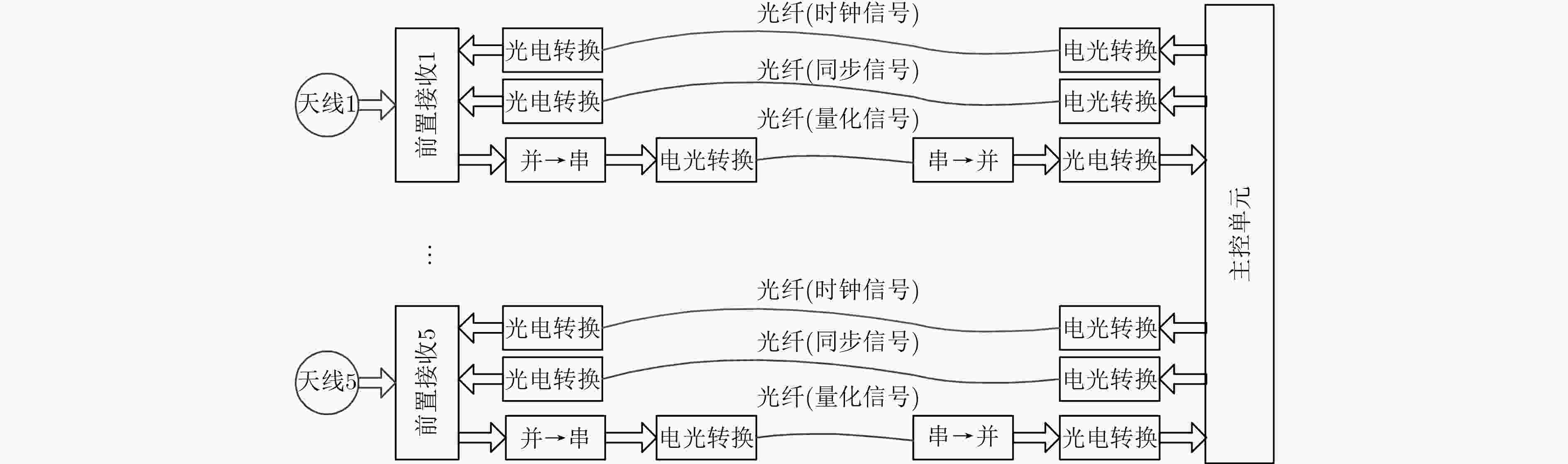
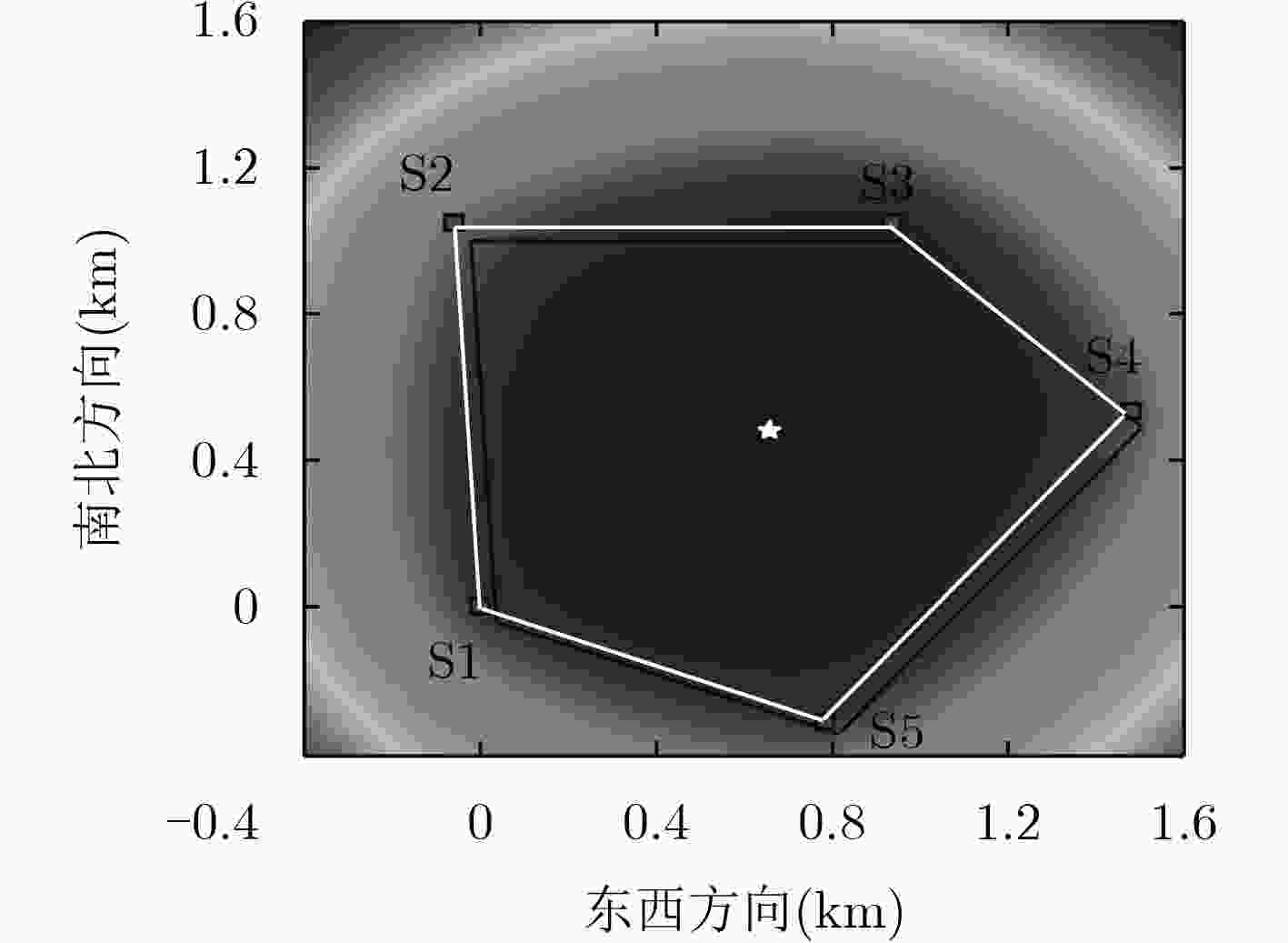
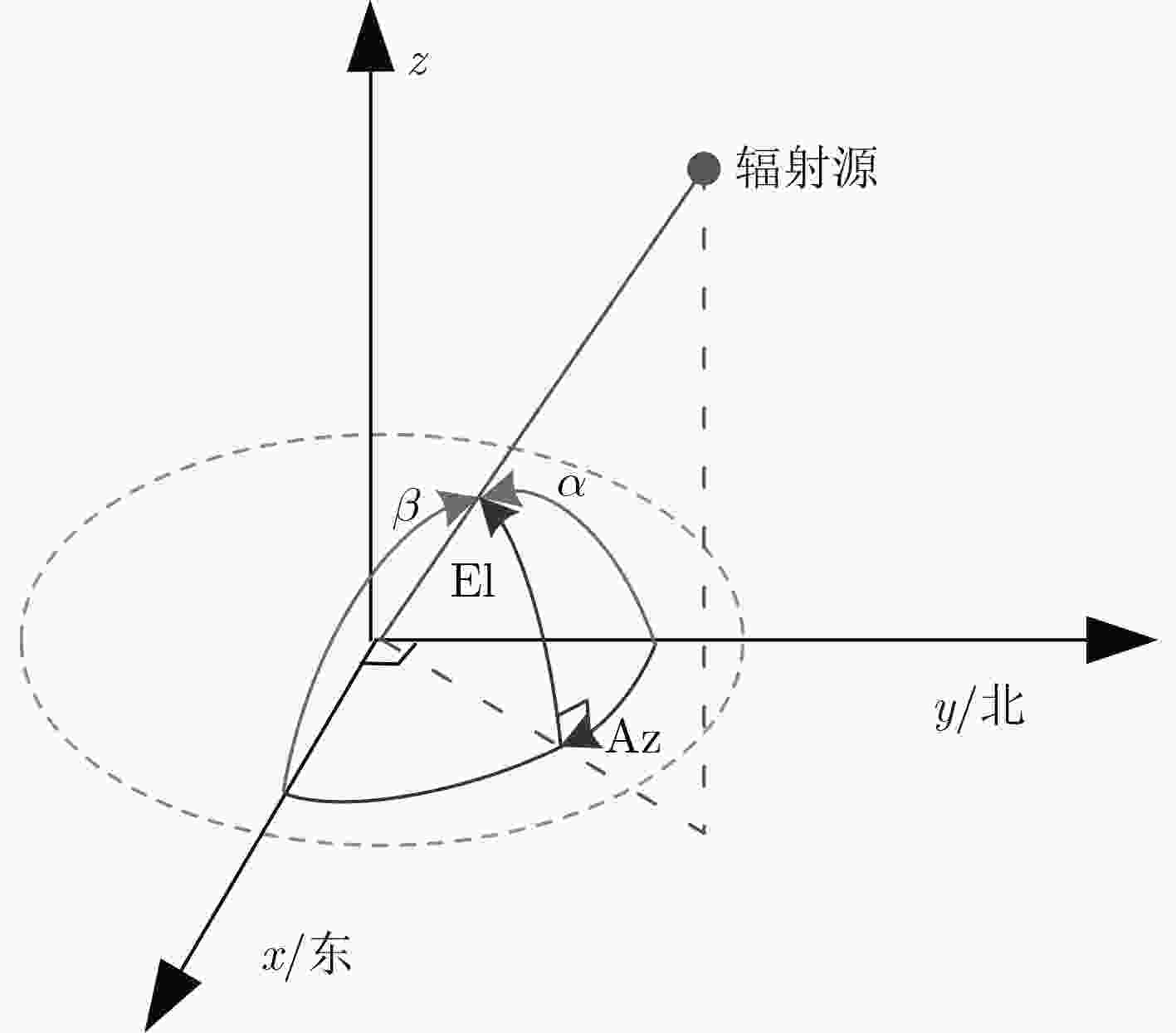
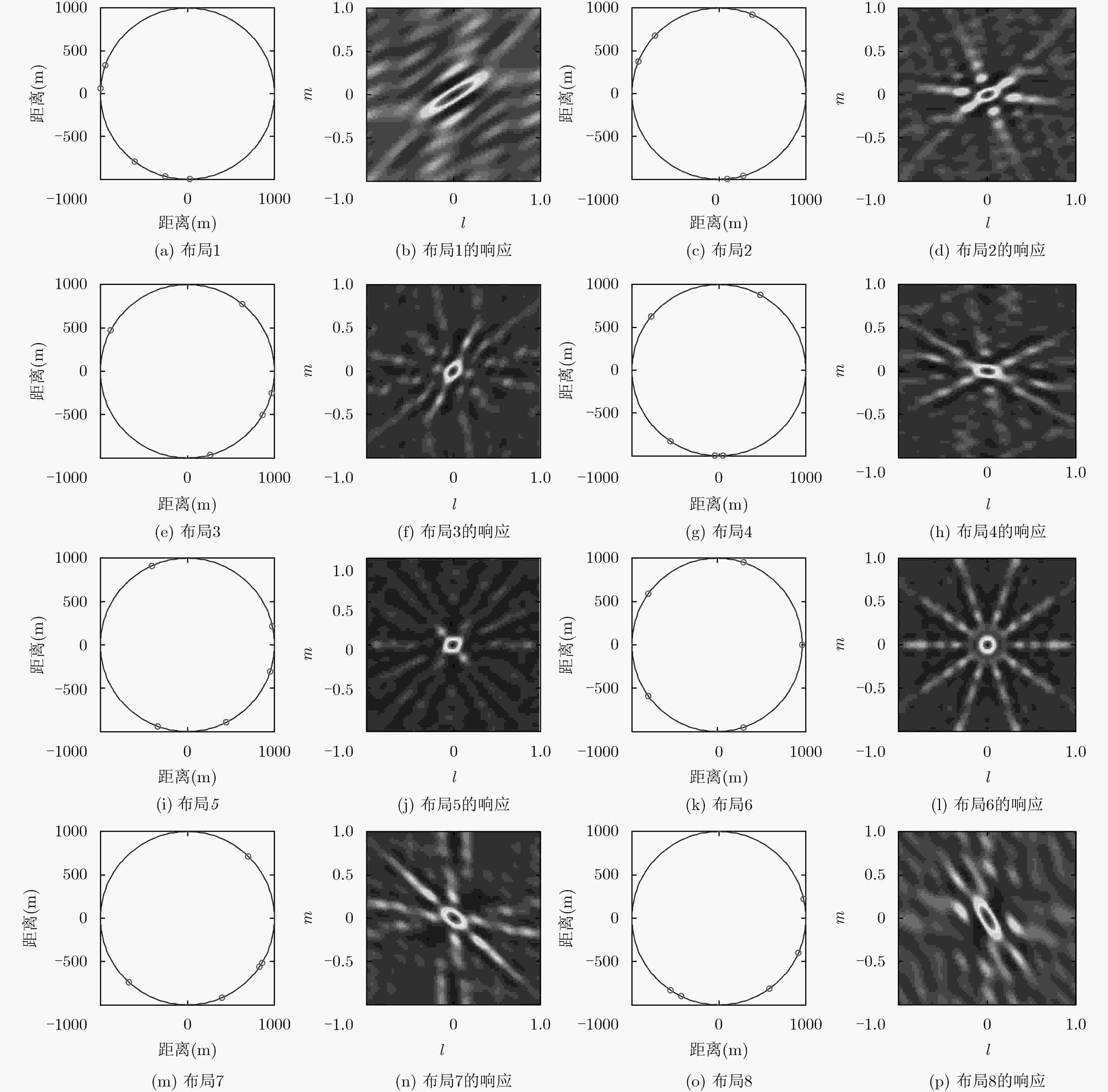
为提高电磁辐射源的定位精度，该文提出一种利用光纤方式同步的超短基线电磁探测阵列(CASMA)。该阵列包括5个电磁探测站和1个控制中心，阵元间距约为1 km(基线长度与波长的比值约为0.1)，同步精度可达10 ns。CASMA用来测量20～70 kHz长波发射电台的垂直电场信号，并利用低频电磁干涉成像算法计算发射电台的方位角。通过实验对比可以发现，估计的发射台方位角与真实发射台方位角之间的误差小于0.2°，远远优于传统的波达角估计方法。因此，CASMA对电磁辐射源具有很高的测向精度。根据实验结果，在2500 km范围内，若两CASMA电磁探测阵对电磁辐射源进行交汇定位，定位精度预期可达0.5%·R(R为探测距离)。
Abstract:To improve the location resolution of electromagnetic radiation source, a ultra-short baseline network CASMA (Mini-Array by Chinese Academy of Sciences) is proposed for detection, utilizing optical fiber for timing. CASMA contains 5 electromagnetic detection stations and a control unit. The distance between each pair of stations is about 1 km, meaning that the length of baseline to the wavelength is about 0.1. The timing accuracy is about 10 ns. CASMA is applied to record the vertical electric field emitting by radio transmitters. CASMA utilizes interferometric imaging algorithm to calculate the transmitters’ azimuth. By experiment, the calculated azimuths approach the expected azimuths with deviations are less than 0.2°, showing many advantages over traditional systems or methods. Consequently, CASMA has accuracy direction finding resolution for electromagnetic radiation source. According to the results, the location accuracy may be expected to be 0.5%·R in a 2500 km scope where R is the distance between the electromagnetic radiation source and CASMA using two sets of CASMA for intersection positioning.
-
Key words:
- Interferometric imaging /
- Very low frequency /
- Super-short baseline
-
1. 引言
在雷暴过程中产生大量闪电电磁脉冲(LEMP)信号，其能量主要分布在甚低频频段(VLF, 3～30 kHz)，可在“地-电离层波导”中传播至数千公里。另一方面，闪电定位系统(LLS)逐渐发展，用来研究各种电磁现象，例如红色精灵[1]、蓝色喷流[2]、放电粒子束[3]及其他现象[4,5]。
最早出现的是甚高频(VHF)闪电定位系统，主要包括VHF窄带干涉系统及宽带干涉系统[6,7]。随着对闪电信号研究的深入认识，低频(VLF/LF)闪电定位系统迅速发展。例如，美国国家LLS[8](National Lightning Detection Network, NLDN)、拉斯莫斯LLS[9](Los Alamos Sferic Array, LASA)、休斯顿阿拉巴马LLS[10](Huntsville Alabama Marx Meter Array, HAMMA)。这些系统的站间距较大，主要用来对阵列中的电磁辐射源定位。Mezentsev等人[11]提出2个低频干涉阵列系统，用来研究100 kHz源的结构。通过探测罗兰台(LORAN)的信号，他们发现当俯仰角为0º时，方位角分辨率约为1°；当俯仰角不为0º时，方位角分辨率约为几度。后来，Füllekrug等人[12]分析对潜通信电台发射的电磁信号的波矢量，并对天空中的电磁噪声源进行成像[13]。他们对VLF电磁信号在“地-电离层波导”中传播时引起的多径效应[14]，相速的变化[15]及闪电成像[16]等方面进行了深入分析与研究。类似地，Lyu等人[17]报告了一种易安置的VLF/LF近场闪电成像系统，站间距约为15～20 km，每个探测站利用两正交的VLF/LF磁天线测量磁场信号。该阵列采用时间差(Time Of Arrival, TOA)技术对闪电进行3维成像，与VHF成像效果显著相同。
鉴于精确定位的需求，本文设计并且部署一套超短基线电磁探测阵列(Mini-Array by Chinese Academy of Sciences, CASMA)。各阵元间的间距约为1 km，基线长度与波长的比约为0.1。该阵列测量VLF/LF频段的垂直电场信号，采用光纤同步方式，时间精度可达10 ns。该阵列采用电磁干涉成像算法，用来测量电磁辐射源的方位角及俯仰角。为检验CASMA阵列的性能，本文利用该阵列测量VLF/LF发射台的垂直电场信号，并将测量方位角与真实方位角进行对比。本文安排如下：首先介绍超短基线电磁探测系统的构成及部署安装；然后介绍VLF/LF宽带电磁干涉算法；最后开展野外实验，测量已知发射电台的方位角。
2. 超短基线电磁探测系统
CASMA采用阵列方式接收电磁场信号，可对辐射源的方位进行定向。该系统由5个接近于均匀分布在半径为1 km圆上的电磁探测站和1个主控单元构成，各探测站和主控单元之间通过光纤连接。各探测站接收来自主控单元的时钟和控制信号，同时将该站收到的电磁脉冲信号数字化后以数字方式通过光纤传送给主控单元，由主控单元统一进行采集和处理。CASMA站点分布如图1所示。
CASMA的工作带宽为1～250 kHz，采样率为2 MHz，按功能可以划分为4个模块，分别为天线模块、前置接收模块、电光-光电转换模块和主控单元模块，其结构功能如图2所示。
天线模块在有效频带范围内天线有效长度为7 m，完成电磁脉冲垂直方向上电场信号的接收，将电场信号转化为电压信号并进行放大处理。
前置接收模块将天线模块接收到的信号进行放大和滤波处理，并根据主控单元发送的时钟和同步信号对模拟信号进行数字化处理。由于通过ADC数字化后的信号为并行信号，而光纤传输的信号为串行信号，因此需要增加并串转换电路。根据设计要求，主控单元提供给各单站的时钟频率为40 MHz，单站模拟信号采集频率为2 MHz，量化位数为14位，这样在1个量化周期内就有足够的时钟周期用来传输数字化后的编码信号。为保证各前置对模拟信号进行数字化时时钟保持一致，设计中尽量采用等长光纤并将所用光纤传播时延控制到10 ns以内。
电光-光电转换模块包括位于单站端的电光转换电路、光纤和位于主控单元端光电转换电路。电光转换电路将前置接收模块数字化后的信号转换成光信号，以便能够在光纤中传输，光电转换电路将光信号转换为电信号并送给主控单元。本设计中，主控单元需要同时与5个单站进行信号传输，每个单站需要接收2路信号，分别为时钟信号和同步信号，同时又将数字化后的电场信号传给主控单元，因此需要设计多种不同的光电和电光转换模块。
主控单元模块为系统的核心，负责给各个单站提供时钟和同步信号，并对光电转换后的信号进行解码，提取出5个单站的有效数据并存储。该阵列通过5路光纤传输至主控单元的数字化编码信号经光电转换后为5路串行数字信号，因此需要首先通过串并转换电路将其转化为ADC量化的并行信号再进行存储和处理。考虑到5路信号的总数据率为20 MB/s，主控单元模块采用了配有高性能FPGA的高速接口板卡实现数据接收，接口板卡安装于高性能工控机上，可以通过波形监控软件查看接收到的电磁脉冲波形。
为了开展电磁探测实验，检验系统的定位测向性能，课题组在内蒙古正镶白旗安装部署了一套超短基线电磁探测系统CASMA，阵元间的最短距离为752 m，最长距离为1093 m，该阵列的最佳点位于(N42.21°，E115.25°)，如图3白色五角星所示。CASMA阵列的几何结构受限于当地草地状况。
3. 电磁干涉成像算法
CASMA系统采用电磁干涉成像算法计算电磁辐射源的方位角。阵元孔径远远小于波长，基线长度与波长的比值约为0.1。因此，电磁信号以平面波的形式扫过各阵元。假设远处某辐射源为
E(t;s) ，它以方向s 平行入射到由N 个阵元组成的电磁脉冲探测阵列，阵列中第i 个和第j 个接收机接收到的电场分别为E(t−τi;s) 和E(t−τj;s) ，其中τi 和τj 分别为源到两个接收机的延时。对2个接收机接收到的信号做互相关处理，互相关谱为
Rij(f)=F[E(t−τi;s)]F∗[E(t−τi;s)]=|˜E(f;s)|2e−j2πf(τi−τj)=|˜E(f;s)|2e−j2πfτij (1) 其中，
F[⋅] 为傅里叶变换算子，˜E(f;s) 为辐射源E(t;s) 的频谱，τij=τi−τj 为辐射源到阵元i 和阵元j 的时间差。当存在多个不相关辐射源时接收信号的互相关谱为
Rij(f)=∫|E(f;s)|2e−j2πfτijds (2) 令阵元
i 到阵元j 的基线矢量为B ，则辐射源到达两接收阵元的时间差可表示为{\tau _{ij}} = (\left{{{{B}} \cdot {{s}}}}\right)/{c} (3) 如图4所示，在xyz坐标系中，Az为以地理北极为起点的方位角；El为相对于水平面的俯仰角；
α ，β 分别为方向角。因此，传播方向s 可以写为s=(cosElsinAz,cosElcosAz,sinEl)=(l,m,√1−l2+m2) (4) 其中，
l=cosα=cosElsinAz ,m=cosβ=cosEl ⋅cosAz 。阵元基线矢量B在xyz坐标系中为B=(xj−xi,yj−yi,zj−zi)=(Δx,Δy,Δz) (5) 利用式(4)和式(5)，互相关谱可重写为
Rij(f)=∫|˜E(f;s)|2e−j2πfτijds=∫|˜E(f;s)|2e−j2πfB⋅scds=∬ (6) 令，
f\left( {l, m} \right) = {\left| {\tilde E(f;l, m)} \right|^2} ,u \!=\! \Delta x\,f/c, v \!=\! \Delta y\,f/c, \Delta z = 0 ，式(6)可改写为F\left( {u, v} \right) = \iint {f\left( {l, m} \right){{\rm e}^{ -{\rm j}2{{π}} ul}}{{\rm e}^{ - {\rm{j}}2{{π}} vm}}{\rm{d}}l {\rm{d}}m} (7) 其中，
F\left( {u, v} \right) = {R_{ij}}\left( f \right) 。从而得到成像计算公式f\left( {l, m} \right) = \iint {F\left( {u, v} \right){{\rm e}^{{\rm{j}}2{{π}} ul}}{{\rm e}^{{\rm j}2{{π}} vm}}{\rm{d}}u {\rm{d}}v} (8) f\left( {l, m} \right) 是在2维方向余弦平面上的图像，对其做坐标变换即可得到方位角Az和俯仰角El平面上的图像{\rm{Az}} = \arctan \left( {l/m} \right) (9) 利用电磁干涉成像算法得到CASMA阵列的系统函数，分布如图5所示。
4. 实验结果
经过一段时间观测后，CASMA获得了大量的电场数据。通过对某1 s内的数据进行功率谱分析，得到如图6的功率谱图。图6中存在的谱密度尖峰为接收到的长波电台信号。长波电台有的用于民用，如68.5 kHz信号为国家天文台设在河南商丘的BPC授时电台信号(SQ)；有的用于军事，如54 kHz信号为位于日本冲绳的对潜通信电台信号。图7为网上公开可查的部分长波电台位置，表1为这些电台相对CASMA电磁探测阵的距离和方位角。
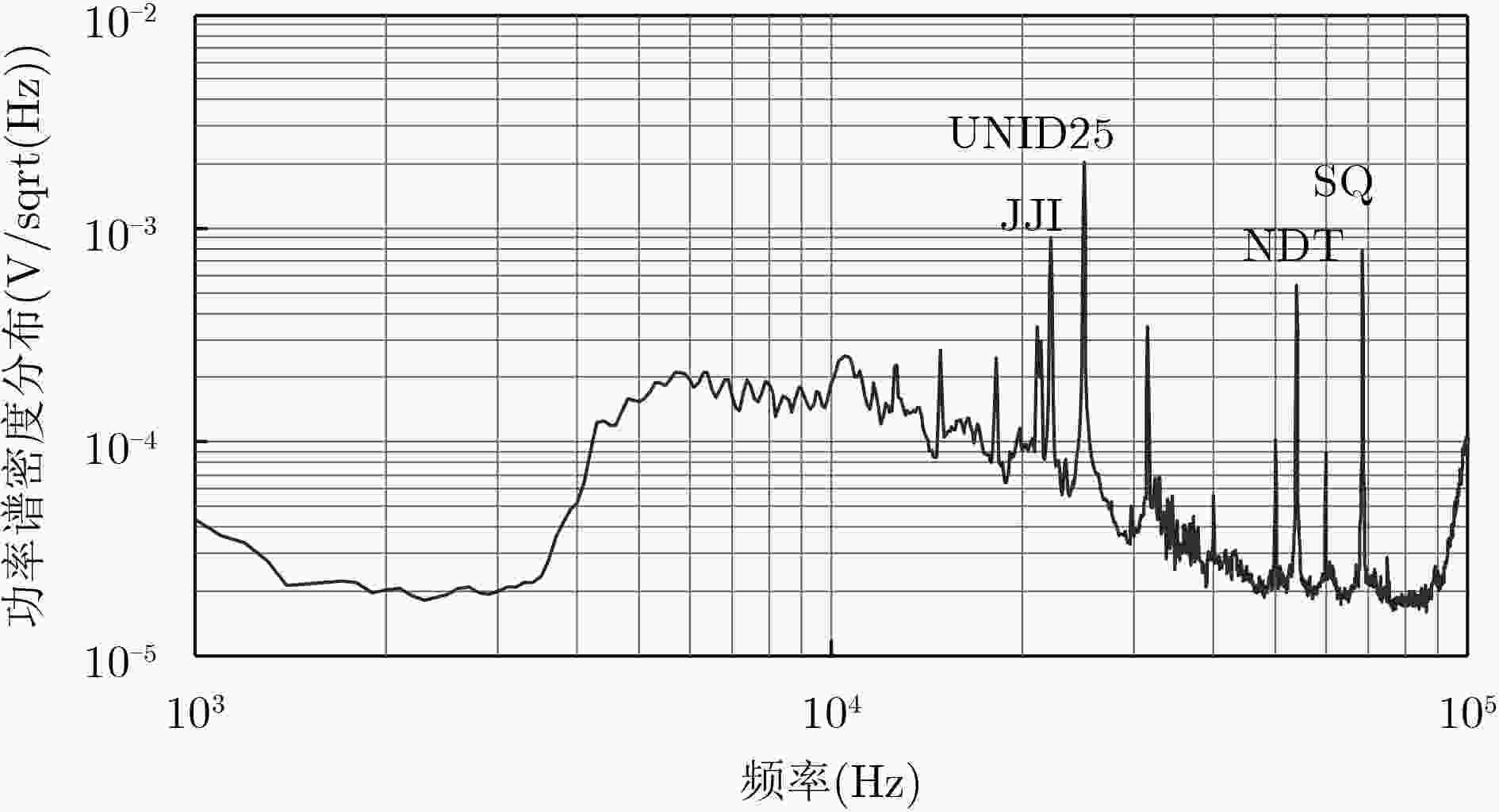
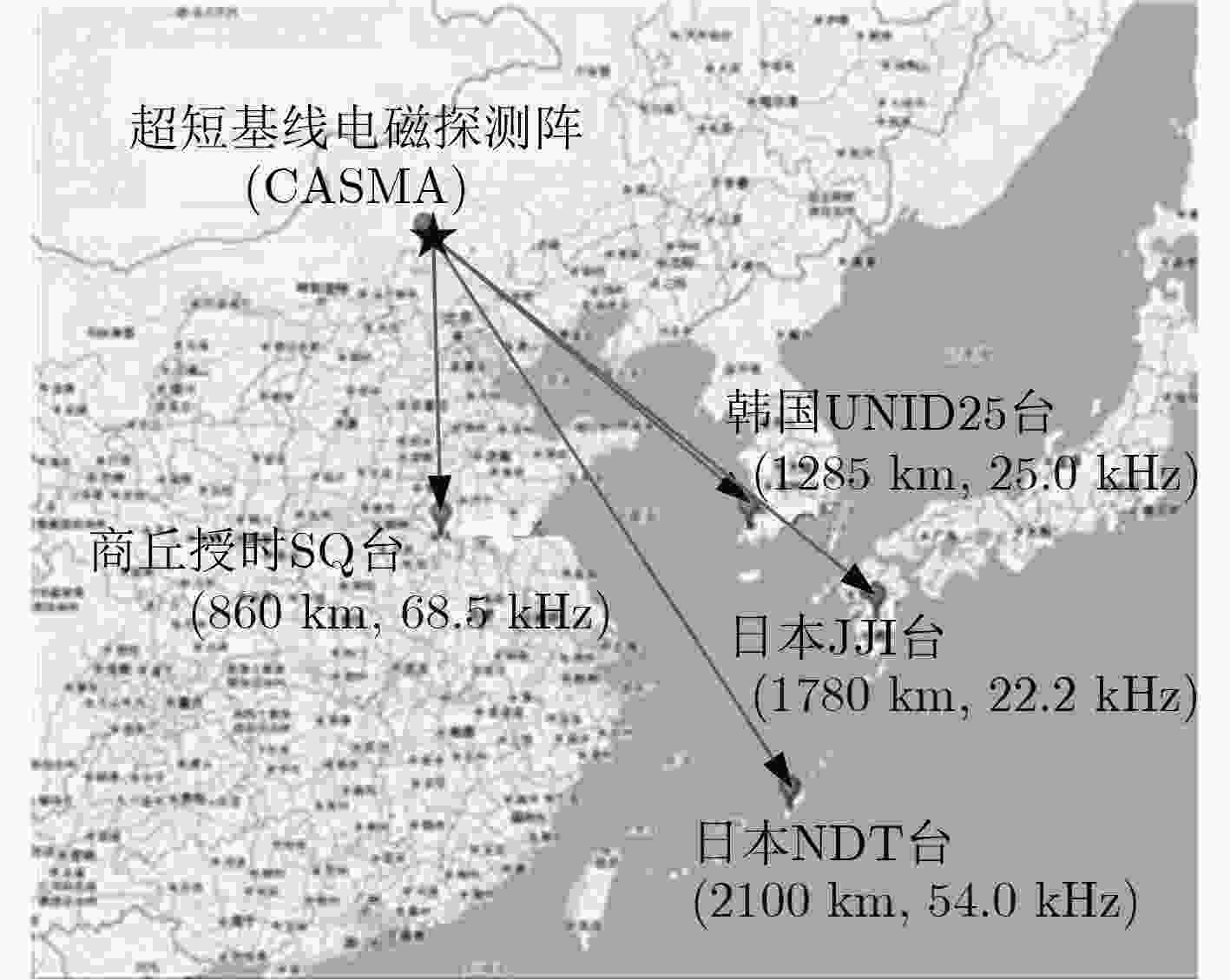
表 1 CASMA电磁探测阵的测向结果名称(台) 工作频率(kHz) 方位角真实值(°) 距离(km) 方位角估计值(°) 方位角误差(°) 方位角标准差(°) SQ 68.5 176.41 862.4 176.29 –0.12 3.55 UNID25 25.0 126.95 1284.2 126.76 –0.19 1.02 JJI 22.2 124.14 1777.9 124.09 –0.05 2.62 NDT 54.0 142.88 2105.2 142.98 0.10 2.37 采用第3节介绍的干涉成像算法对采集到的电台信号进行处理，得到各个电台所在位置相对CASMA电磁探测阵的方位角，结果如表1所示。其中，方位角真实值为根据网上公开的VLF电台经纬度位置计算的，方位角估计值为采用干涉成像算法得到的，两者的误差及标准差见表1。由此可见，CASMA电磁探测阵对于这4个频率的长波电台测向结果误差均在0.2º以内。
5. 讨论与分析
5.1 阵列布局
为了对系统阵列布局的影响进行分析，仿真中假定阵元个数为5个，阵元分布在半径为1 km的圆上，通过改变站点之间的距离使得阵列的布局形式发生改变，阵列布局及仿真结果如图8所示。
图8中圆的半径为1 km，实点为接收站点的位置，阵列布局与阵列响应一一对应。从图8中可以看到，不同的阵列布局对应不同的阵列响应，阵列响应代表了阵列的方向性和分辨率。以图8(a)和图8(b)为例，图8(a)为阵列的布局形式，图8(b)为图8(a)对应的阵列响应。从图8(b)中可以看出，该阵列布局使得系统不具备全向性，对左下–右上方向的来波分辨率较高；对左上–右下方向的来波分辨率较低；因此，该阵列形式适用于探测左下–右上方向的电磁辐射源。同理，对于5站点均匀分布的图8(k)和图8(l)而言，阵列响应具有全向性，即系统在各个方向上的响应一致，且分辨率一致，该阵列布局形式适用于探测未知方向的电磁辐射源。因此，若保持站点个数不变，改变阵列布局会改变阵列的方向性和分辨率，阵列布局是阵列方向性和分辨率的折中体现。当电磁辐射源方位未知时，宜采用均匀分布阵列；当电磁辐射源方位已知或重点探测某方位时，可牺牲阵列方向性，对阵列布局进行优化，达到提升分辨率的目的。
5.2 系统方位角误差
对于干涉系统而言，影响角度误差的因素主要包括阵列布局与时间差误差。CASMA系统各阵元近似均匀分布，系统响应如图5所示，近似具有全向性，对各个方向上的来波分辨率一致。系统的方位角误差与时间差误差之间的关系为[6]
{\sigma _ {\rm{Az}}} = \frac{\rm c}{d}\frac{1}{{\cos \left( {{\rm{El}}} \right)}}{\sigma _\tau } (10) 其中，c为光速，d为最大阵元间距，El为俯仰角，
{\sigma _\tau } 为时间误差。影响时间差的因素主要包括系统同步误差，时间差提取误差，采样误差等。本文重点对系统的同步误差进行分析。(1)采样误差：CASMA系统的采样率为2 MHz，采样间隔为0.5 μs。本文采用相关技术提取各阵元间的时间差。在相关操作之前，对采样数据进行500倍的上采样，使得采样间隔为1 ns。因此，采样误差对提取各阵元间的时间差影响不大。
(2)时间差提取误差：本文采用相关技术提取两通道间的时间差，该技术与积分时间、工作带宽、信噪比等有关，其克拉-美罗界(CRLB)可利用Carter的工作进行估算[18]
\sigma _ {\rm{corr}}^2 \ge \frac{1}{{2T\displaystyle\int_{{f_1}}^{{f_2}} {{{\left( {2{{π}} f} \right)}^2}\displaystyle\frac{{{{\left( {\rm{SNR}} \right)}^2}}}{{1 + 2 {\rm{SNR}}}}{\rm{d}}f} }} (11) 其中，T是积分时间，
{f_1} 和{f_2} 是工作带宽的上下限，SNR是信噪比。(3)系统同步误差：CASMA系统采用光纤同步方式，5个阵元在同一时钟及复位信号控制下同步工作，同步精度高。测试方法为：信号源输出不同频率的正弦信号，分5路馈入不同的接收机，采样得到的数字信号经光缆传输到数据处理中心，经解码后得到信号波形，统计分析不同信号通道间的时间差。时间同步精度(标准差)测试结果见表2。从测试结果中可以看到，在大部分频点处，系统同步精度高；在部分频点(如10 kHz)，系统同步精度较差。因此，在整个频带内，系统的同步精度优于10 ns。
表 2 同步精度测试结果(ns)频率(kHz) (1, 2) (1, 3) (1, 4) (2, 3) (2, 4) (3, 4) 1 0.0 0.0 0.0 0.0 0.0 0.0 2 0.0 0.0 0.0 0.0 0.0 0.0 5 0.0 0.0 0.0 0.0 0.0 0.0 10 0.0 9.1 7.4 11.4 9.3 0.0 20 3.4 2.6 3.7 2.2 2.5 0.0 30 2.1 2.1 1.8 2.5 1.6 0.0 40 1.4 1.2 1.2 1.8 1.2 0.0 50 1.1 1.5 0.5 1.3 1.3 0.0 60 0.8 0.8 0.9 1.0 0.8 0.0 70 1.1 0.8 0.8 1.0 0.9 0.0 80 0.8 0.8 1.0 0.6 0.7 0.7 90 0.6 0.5 0.5 0.7 0.7 0.0 100 0.6 0.5 0.6 0.6 0.6 0.0 200 0.2 0.3 0.3 0.3 0.3 0.0 该系统在某发射源工作频点处的时间同步精度如表3所示。
表 3 在某固定频点处的同步精度发射源 工作频率(kHz) 系统同步精度(ns) 商丘授时SQ 68.5 ～1 韩国UNID25 25.0 ～2 日本JJI 22.2 ～3 日本NDT 54.0 ～1 综上所述，对于CASMA系统而言，在SQ, JJI, NDT, UNID25等发射台的工作频点处，同步精度优于3 ns。在理想情况下(仅考虑系统的时间同步精度误差)，方位角误差的CRLB为0.045°。实际工作过程中，发射源带宽、能量不稳定性和传播路径不均匀性使得系统的方位角误差增大。
6. 结束语
本文设计并部署1套超短基线电磁探测阵列CASMA。CASMA包括5个电磁探测站和1个控制中心。阵元间距约为1 km，采用光纤同步方式，同步精度优于10 ns。CASMA采用电磁干涉成像算法对电磁辐射源成像，通过测量已知位置的长波发射电台信号，得到方位角误差小于0.2°。因此，在2500 km的范围内，若利用2个CASMA电磁探测阵进行交汇定位，定位误差约为0.5%·R(R为探测距离)，此定位精度远远优于传统闪电定位系统。同时，CASMA电磁探测阵列也可用于刻画闪电的发展过程，对闪电通道进行精细成像。
-
表 1 CASMA电磁探测阵的测向结果
名称(台) 工作频率(kHz) 方位角真实值(°) 距离(km) 方位角估计值(°) 方位角误差(°) 方位角标准差(°) SQ 68.5 176.41 862.4 176.29 –0.12 3.55 UNID25 25.0 126.95 1284.2 126.76 –0.19 1.02 JJI 22.2 124.14 1777.9 124.09 –0.05 2.62 NDT 54.0 142.88 2105.2 142.98 0.10 2.37 
下载: 导出CSV
表 2 同步精度测试结果(ns)
频率(kHz) (1, 2) (1, 3) (1, 4) (2, 3) (2, 4) (3, 4) 1 0.0 0.0 0.0 0.0 0.0 0.0 2 0.0 0.0 0.0 0.0 0.0 0.0 5 0.0 0.0 0.0 0.0 0.0 0.0 10 0.0 9.1 7.4 11.4 9.3 0.0 20 3.4 2.6 3.7 2.2 2.5 0.0 30 2.1 2.1 1.8 2.5 1.6 0.0 40 1.4 1.2 1.2 1.8 1.2 0.0 50 1.1 1.5 0.5 1.3 1.3 0.0 60 0.8 0.8 0.9 1.0 0.8 0.0 70 1.1 0.8 0.8 1.0 0.9 0.0 80 0.8 0.8 1.0 0.6 0.7 0.7 90 0.6 0.5 0.5 0.7 0.7 0.0 100 0.6 0.5 0.6 0.6 0.6 0.0 200 0.2 0.3 0.3 0.3 0.3 0.0
下载: 导出CSV
-
CUMMER S and FULLEKRUG M. Unusually intense continuing current in lightning produces delayed mesospheric breakdown[J]. Geophysics Research Letter, 2001, 28(3): 495–498 doi: 10.1029/2000GL012214 CUMMER S, LI Jingbo, HAN Feng, et al. Quantification of the troposphere-to-ionosphere charge transfer in a gigantic jet[J]. Nature Geoscience, 2009, 2(9): 617–620 doi: 10.1038/NGEO607 FULLEKRUG M, ROUSSELDUPRE R, SYMBALISTY E M D, et al. Relativistic electron beams above thunderclouds[J]. Atmospheric Chemistry & Physics & Discussions, 2011, 11(15): 7747–7754 doi: 10.5194/acp-11-7747-2011 GEMELOS E S, INAN U S, WALT M, et al. Seasonal dependence of energetic electron precipitation: Evidence for a global role of lightning[J]. Geophysical Research Letters, 2009, 36(21): 147–148 doi: 10.1029/2009GL040396 QIN Jianqi, CELESTIN S, and PASKO V P. Low frequency electromagnetic radiation from sprite streamers[J]. Geophysical Research Letters, 2012, 39(22): 1–5 doi: 10.1029/2012GL053991 STOCK M G, AKITA M, RISON W, et al. Continuous broadband digital interferometry of lightning using a generalized cross-correlation algorithm[J]. Journal of Geophysical Research Atmospheres, 2014, 119(6): 3134–3165 doi: 10.1002/2013JD020217 THOMAS R J, KREHBIEL P R, RISON W, et al. Accuracy of the lightning mapping array[J]. Journal of Geophysical Research Atmospheres, 2004, 109(D14): 1–34 doi: 10.1029/2004JD004549 CUMMINS K L, MURPHY M J, BARDO E A, et al. A combined TOA/MDF technology upgrade of the U.S. national lightning detection network[J]. Journal of Geophysical Research Atmospheres, 1998, 103(D8): 9035–9044 doi: 10.1029/98JD00153 SMITH D A, EACK K B, HARLIN J, et al. The Los Alamos Sferic Array: A research tool for lightning investigations[J]. Journal of Geophysical Research Atmospheres, 2002, 107(D13): 5–14 doi: 10.1029/2001JD000502 BITZER P M, CHRISTIAN H J, STEWART M, et al. Characterization and applications of VLF/LF source locations from lightning using the Huntsville Alabama Marx Meter Array[J]. Journal of Geophysical Research Atmospheres, 2013, 118(8): 3120–3138 doi: 10.1002/jgrd.50271 MEZENTSEV A and FULLEKRUG M. Mapping the radio sky with an interferometric network of low‐frequency radio receivers[J]. Journal of Geophysical Research Atmospheres, 2013, 118(15): 8390–8398 doi: 10.1002/jgrd.50671 FULLEKRUG M, MEZENTSEV A, WATSON R, et al. Array analysis of electromagnetic radiation from radio transmitters for submarine communication[J]. Geophysical Research Letters, 2014, 41(24): 9143–9149 doi: 10.1002/2014GL062126 FULLEKRUG M, MEZENTSEV A, WATSON R, et al. Map of low frequency electromagnetic noise in the sky[J]. Geophysical Research Letters, 2015, 42(11): 4648–4653 doi: 10.1002/2015GL064142 FULLEKRUG M, SMITH N, MEZENTSEV A, et al. Multipath propagation of low frequency radio waves inferred from high resolution array analysis[J]. Radio Science, 2015, 50(11): 1141–1149 doi: 10.1002/2015RS005781 LIU Zhongjian, KUANG L K, MEZENTSEV A, et al. Variable phase propagation velocity for long-range lightning location system[J]. Radio Science, 2016, 51(11): 1806–1815 doi: 10.1002/2016RS006058 FULLEKRUG M, LIU Zhongjian, KOH K, et al. Mapping lightning in the sky with a mini array[J]. Geophysical Research Letters, 2016, 43(19): 10448–10454 doi: 10.1002/2016GL070737 LYU Fanchao, CUMMER S A, SOLANKI R, et al. A low‐frequency near‐field interferometric TOA 3D Lightning Mapping Array[J]. Geophysical Research Letters, 2014, 41(22): 7777–7784 doi: 10.1002/2014GL061963 CARTER G C. Coherence and time delay estimation[J]. Proceedings of the IEEE, 1987, 75(2): 236–255 doi: 10.1109/PROC.1987.13723 期刊类型引用(1)
1. 罗春兰，林文，祝晓霞. (47, 24, 11)QR码的快速代数译码算法. 三明学院学报. 2022(06): 60-66+78 . 
百度学术其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 2190
- HTML全文浏览量: 685
- PDF下载量: 66
- 被引次数: 2
下载:
