多尺度局部结构主导二值模式学习图像表示

张东波; 易良玲; 许海霞; 张莹

doi:10.11999/JEIT180512

多尺度局部结构主导二值模式学习图像表示

doi: 10.11999/JEIT180512

1.
湘潭大学信息工程学院湘潭 411105
2.
机器人视觉感知与控制国家工程实验室长沙 410012

基金项目: 国家自然科学基金(61602397)，湖南省自然科学基金(2017JJ2251, 2017JJ3315)，湖南省重点学科建设项目

详细信息

作者简介:
张东波：男，1973年生，博士，教授，研究方向为计算机视觉、模式识别

易良玲：女，1993年生，硕士，研究方向为计算机视觉、机器学习

许海霞：女，1979年生，博士，副教授，研究方向为机器视觉、模式识别

张莹：男，1972年生，博士，副教授，研究方向为机器人控制、模式识别、高维可视化处理

通讯作者:
张东波　zhadonbo@163.com

中图分类号: TP391.4
计量
- 文章访问数: 1827
- HTML全文浏览量: 529
- PDF下载量: 60
- 被引次数: 0
出版历程
- 收稿日期: 2018-05-25
- 修回日期: 2018-12-18
- 网络出版日期: 2018-12-25
- 刊出日期: 2019-04-01

Multi-scale Local Region Structure Dominant Binary Pattern Learning for Image Representation

1.
College of Information Engineering, Xiangtan University, Xiangtan 411105, China
2.
Robot Visual Perception & Control Technology National Engineering Laboratory, Changsha 410012, China

Funds: The National Natural Science Foundation of China (61602397), The Natural Science Foundation of Hunan Province (2017JJ2251, 2017JJ3315), The Key Discipline Construction Project of Hunan Province

摘要

摘要:
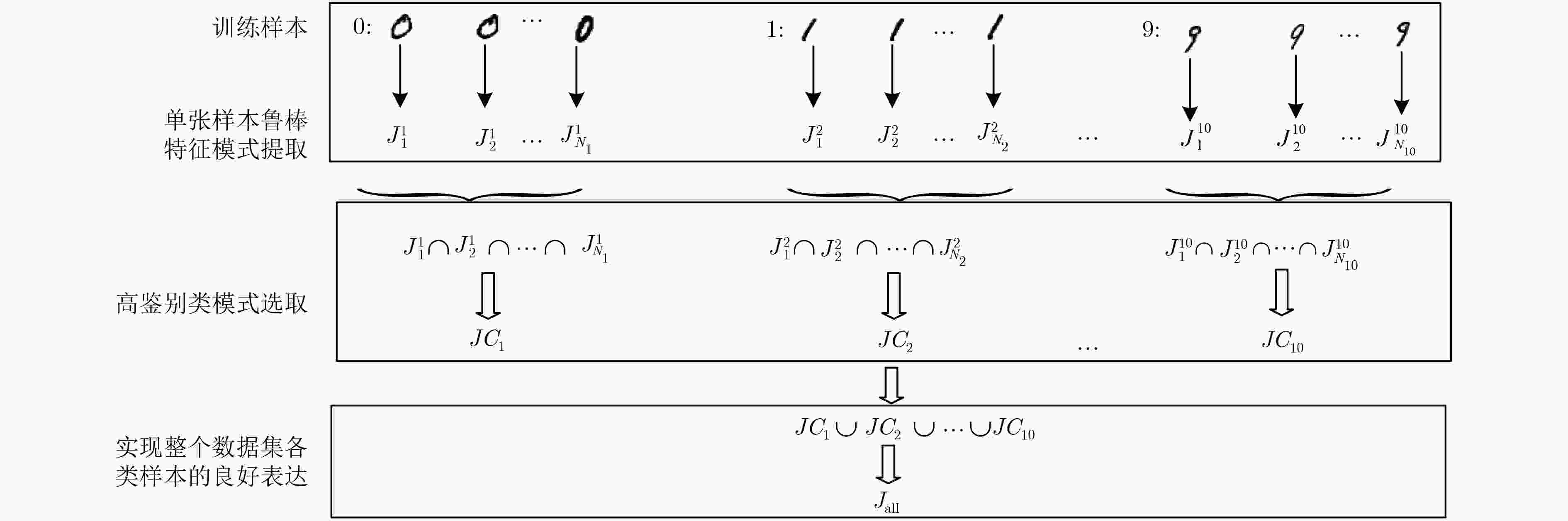
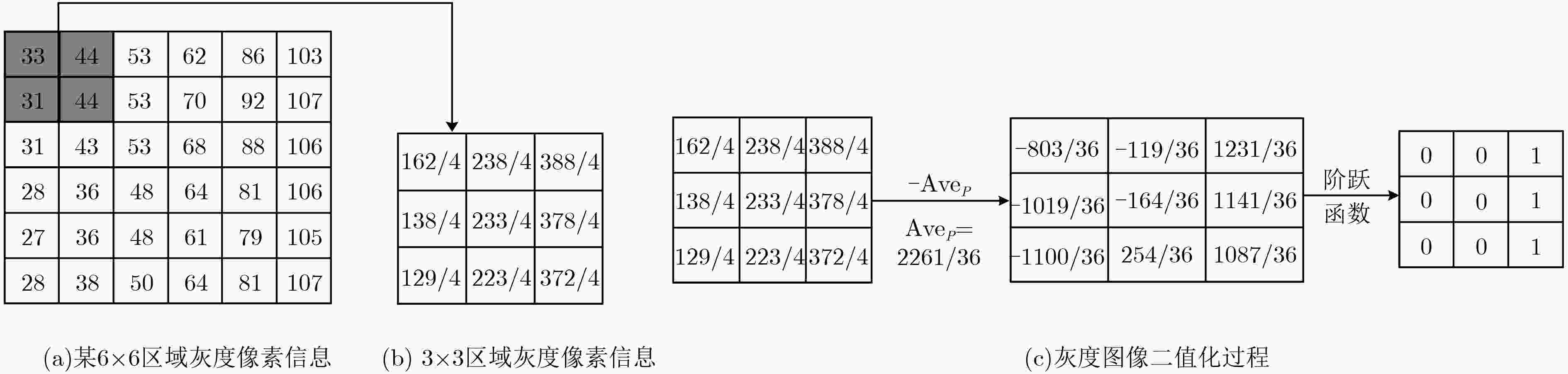
通过零均值化的微观结构模式二值化(ZMPB)处理，该文提出一种立足于局部图像多尺度结构二值模式提取的图像表示方法。该方法能够表达图像中可能出现的各种具有视觉意义的重要模式结构，同时通过主导二值模式学习模型，可以获得适应于图像数据集的主导特征模式子集，在特征鲁棒性、鉴别力和表达能力上达到优异性能，同时可以有效降低特征编码的维度，提高算法的执行速度。实验结果表明该算法性能优异，具有很强的鉴别能力和鲁棒性，优于传统LBP和GIMMRP方法，和很多最新算法结果相比，也具有竞争优势。
- 目标识别 /
- 零均值化的微观结构模式二值化 /
- 主导二值模式学习 /
- 局部结构
Abstract:
By means of Zero-mean Microstructure Pattern Binarization (ZMPB), an image representation method based on image local microstructure binary pattern extraction is proposed. The method can express all the important patterns with visual meaning that may occur in the image. Moreover, through the dominant binary pattern learning model, the dominant feature pattern set adapted to the different data sets is obtained, which not noly achieves excellent ability in feature robustness, discriminative and representation, but also can greatly reduce the dimension of feature coding and improve the execution speed of the algorithm. The experimental results show that the proposed method has strong discriminative power and outperformes the traditional LBP and GIMMRP methods. Compared with many recent algorithms, the proposed method also presents a competitive advantage.
- Object recognition /
- Zero-mean Microstructure Pattern Binarization (ZMPB) /
- Dominant binary pattern learning /
- Local region structure

HTML全文

图 1 模式示例图

下载: 全尺寸图片幻灯片

图 2 ZMPB模式计算示例

下载: 全尺寸图片幻灯片

图 3 主导模式学习模型

下载: 全尺寸图片幻灯片

图 4 空间池化示意图

下载: 全尺寸图片幻灯片

图 5 2×2分块下ZMPB模式值计算示例图

下载: 全尺寸图片幻灯片

表 1 各种算法人脸识别率比较(%)

识别算法	ORL	YALE
LBP	96.00	92.96
ART^[10]	87.70	85.20
SRMKVS^[11]	96.18	93.79
ACNN^[12]	95.00	–
ALDRC^[13]	96.50	–
DTSA^[14]	96.68	71.09
EMKFDA^[15]	97.50	78.44
HOG^[16]	96.00	93.67
SHAO等人方法^[17]	97.50	97.50
GIMMRP^[9]	97.50	94.11
本文算法	99.40	99.30

下载: 导出CSV

表 2 各种算法在手写数字库MNIST的识别率比较(%)

识别算法	MNIST
LBP	93.56
CKELM^[18]	96.80
MPDA^[19]	89.91
WU等人方法^[20]	87.64
LIB-LLSVM+C-OCC^[21]	98.39
MCDNN^[22]	99.77
HOG^[23]	97.25
GIMMRP^[9]	98.91
本文算法	99.01

下载: 导出CSV

表 3 各种算法的车标识别率比较(%)

	训练样本数
	10	20	30	40	50
LBP	97.95	99.42	99.69	99.87	99.92
GIMMRP^[9]	99.64	99.88	99.95	99.96	99.96
本文算法	99.87	99.98	100	100	100

下载: 导出CSV

表 4 本文算法与相关算法性能比较

数据库		1×1识别率(%)	2×2识别率(%)	1×1+2×2识别率(%)	特征维度	1×1尺度单张图片特征提取时间(s)
YALE	本文算法	95.56	95.40	99.30	4050/5670/9720	0.020
	LBP	92.96			4779	0.016
	GIMMRP	94.11			10611	0.062
ORL	本文算法	97.70	97.45	99.40	7290/6966/14256	0.020
	LBP	96.00			4779	0.016
	GIMMRP	97.50			10611	0.061
车标	本文算法	99.11	99.10	99.76	4212/5670/9882	0.018
	LBP	97.95			4779	0.012
	GIMMRP	99.64			10611	0.053
MNIST	本文算法	98.32	98.93	99.01	720/792/1512	0.016
	LBP	93.56			2124	0.015
	GIMMRP	98.91			4716	0.044

下载: 导出CSV

参考文献(23)

LOWE D G. Distinctive image features from scale-invariant key points[J]. International Journal of Computer Vision, 2004, 60(2): 91–110 doi: 10.1023/B:VISI.0000029664.99615.94

BAY H and TUYTELAARS T. SURF: Speeded up robust features[J]. Computer Vision & Image Understanding, 2006, 110(3): 404–417 doi: 10.1007/11744023_32

MIKOLAJCZYK K and SCHMID C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615–1630 doi: 10.1109/TPAMI.2005.188

ENGIN T, LEPETIT V, and FUA P. Daisy: An efficient dense descriptor applied to wide-baseline stereo[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 815–830 doi: 10.1109/TPAMI.2009.77

DALAL N and TRIGGS B. Histograms of oriented gradients for human detection[C]. IEEE Computer Society Conference on Computer Vision & Pattern Recognition, San Francisco, USA, 2005: 886–893.

OJALA T, VALKEALAHTI K, OJA E, et al. Texture discrimination with multidimensional distributions of signed gray-level differences[J]. Pattern Recognition, 2001, 34(3): 727–739 doi: 10.1016/S0031-3203(00)00010-8

OJALA T, PIETIKAINEN M, and MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971–987 doi: 10.1109/TPAMI.2002.1017623

LIAO S, LAW M W K, and CHUNG A C S. Dominant local binary patterns for texture classification[J]. IEEE Transactionson Image Processing, 2009, 18(5): 1107–1118 doi: 10.1109/TIP.2009.2015682

张东波, 陈治强, 易良玲, 等. 图像微观结构的二值化表示与目标识别应用[J]. 电子与信息学报, 2018, 40(3): 633–640 doi: 10.11999/JEIT170513

ZHANG Dongbo, CHEN Zhiqiang, YI Liangling, et al. Binarization representation of image microstructure and the application of object recognition[J]. Journal of Electronics &Information Technology, 2018, 40(3): 633–640 doi: 10.11999/JEIT170513

HAMDAN B and MOKHTAR K. Face recognition using Angular Radial Transform[J]. Journal of King Saud University-Computer and Information Sciences, 2016, 30(2): 141–151 doi: 10.1016/j.jksuci.2016.10.006

ZHU Ningbo, TANG Ting, and TANG Shi. A sparse representation method based on kernel and virtual samples for face recognition[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(23): 6236–6241 doi: 10.1016/j.ijleo.2013.05.017

ZHANG Yuanyuan and ZHAO Dong. Adaptive convolutional neural network and its application in face recognition[J]. Neural Processing Letters, 2016, 43(2): 389–399 doi: 10.1007/s11063-015-9420-y

HUANG Pu and LAI Zhihui. Adaptive linear discriminant regression classification for face recognition[J]. Digital Signal Processing, 2016, 55: 78–84 doi: 10.1016/j.dsp.2016.05.001

WANG Sujing and ZHOU Chunguang. Face recognition using second-order discriminant tensor subspace analysis[J]. Neurocomputing, 2011, 74(12/13): 2142–2156 doi: 10.1016/j.neucom.2011.01.024

WANG Guoqiang and SHI Nianfeng. Embedded manifold-based kernel fisher discriminant analysis for face recognition[J]. Neural Processing Letters, 2016, 43(1): 1–16 doi: 10.1007/s11063-014-9398-x

SINGH G and CHHABRA I. Integrating global zernike and local discriminative HOG features for face recognition[J]. International Journal of Image & Graphics, 2016, 16(4): 1650021–1650042 doi: 10.1142/S0219467816500212

SHAO Hong and CHEN Shuang. Face recognition based on subset selection via metric learning on manifold[J]. Frontiers of Information Technology & Electronic Engineering, 2015, 16(12): 1046–1058 doi: 10.1631/FITEE.1500085

DING Shifei and GUO Lili. Extreme learning machine with kernel model based on deep learning[J]. Neural Computing & Applications, 2017, 28(8): 1975–1984 doi: 10.1007/s00521-015-2170-y

ZHOU Yang and SUN Shiliang. Manifold partition discriminant analysis[J]. IEEE Transactions on Cybernetics, 2017, 47(4): 830–840 doi: 10.1109/TCYB.2016.2529299

WU Tingfang and LIN C J. Probability estimates for multi-class classification by pairwise coupling[J]. Journal of Machine Learning Research, 2004, 5(4): 975–1005.

SCHMIDHUBER J, CIRES D, and MEIER U. Multi-column deep neural networks for image classification[C]. IEEE Conference on Computer Vision & Pattern Recognition, Rod Aprovendis, USA, 2012: 3642–3649.

ZHANG Ziming and LADICKY L. Learning anchor planes for Classification[C]. Advances in Neural Information Processing Systems, Granada, Spain, 2011: 1611–1619.

EBRAHIMZADEH R and JAMPOUR M. Efficient handwritten digit recognition based on histogram of oriented gradients and SVM[J]. Annals of the Rheumatic Diseases, 2014, 104(9): 10–13 doi: 10.5120/18229-9167

施引文献

资源附件(0)

访问统计