DOA Estimation Under Active Deception Jamming Environment
-
摘要:
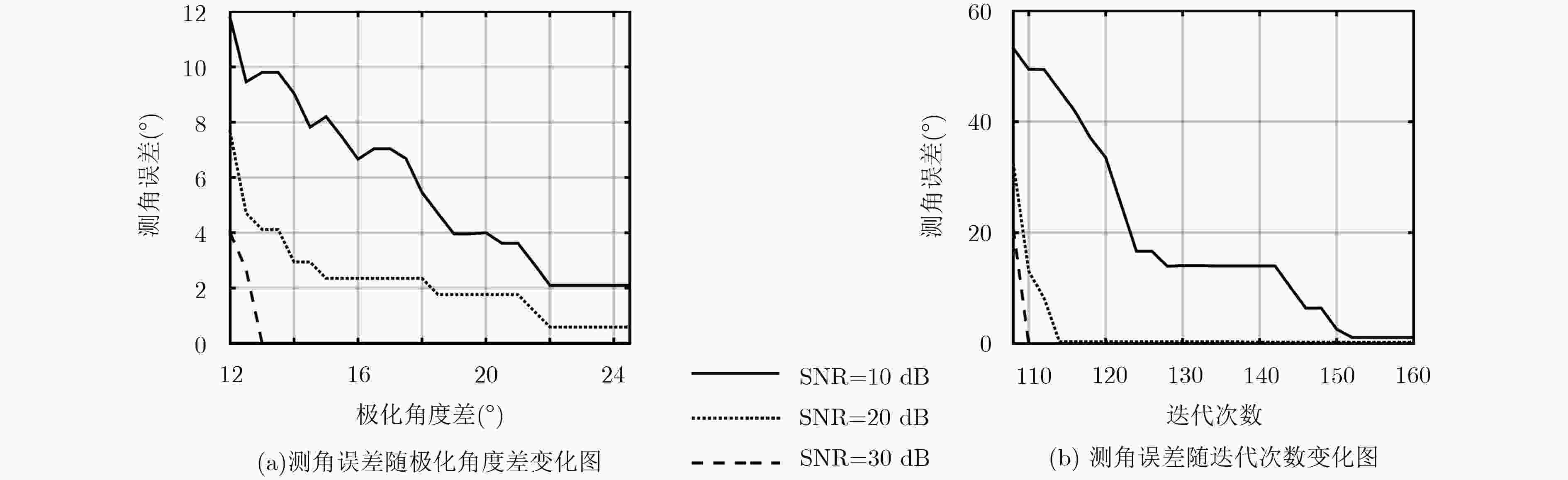
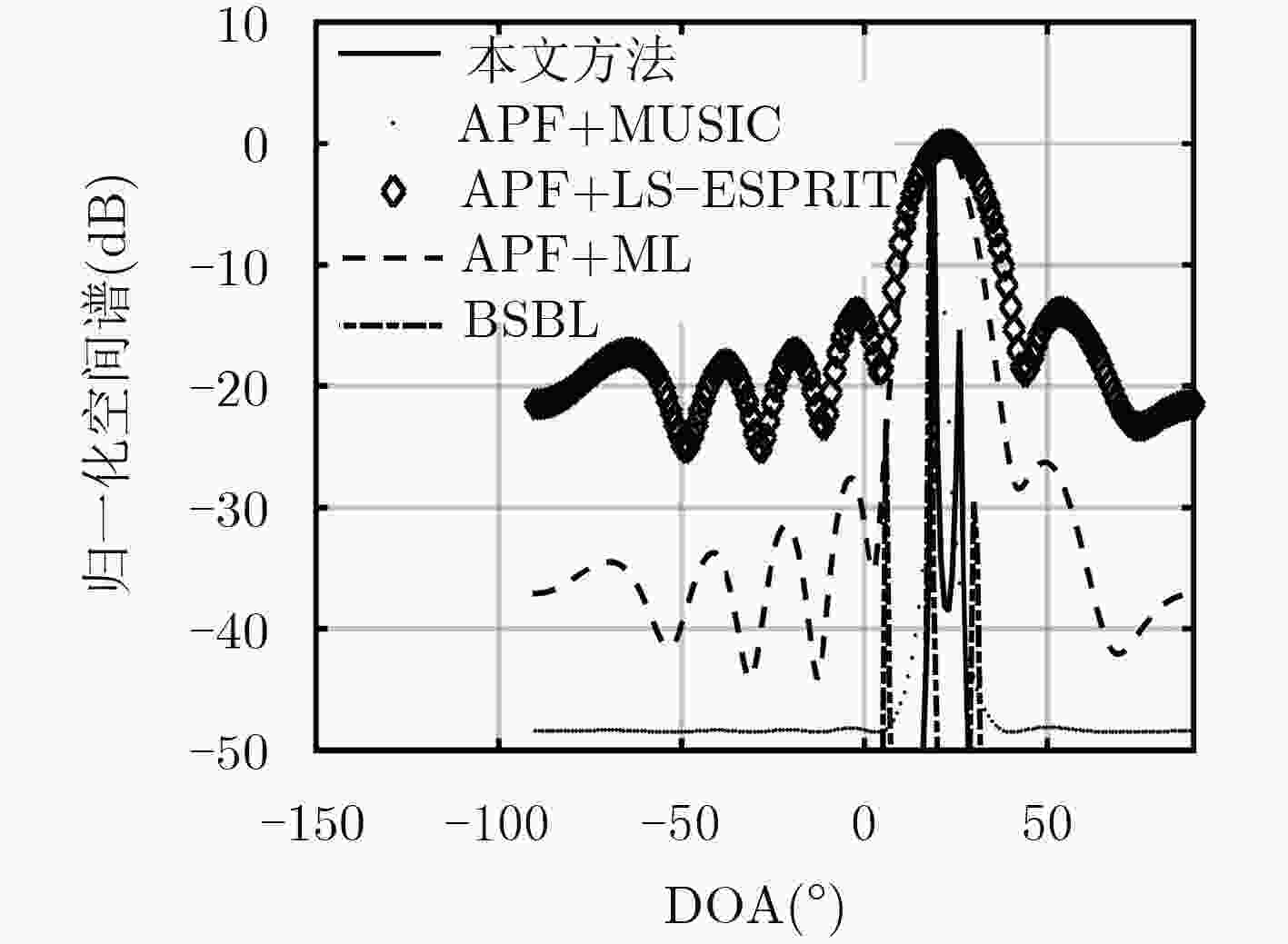
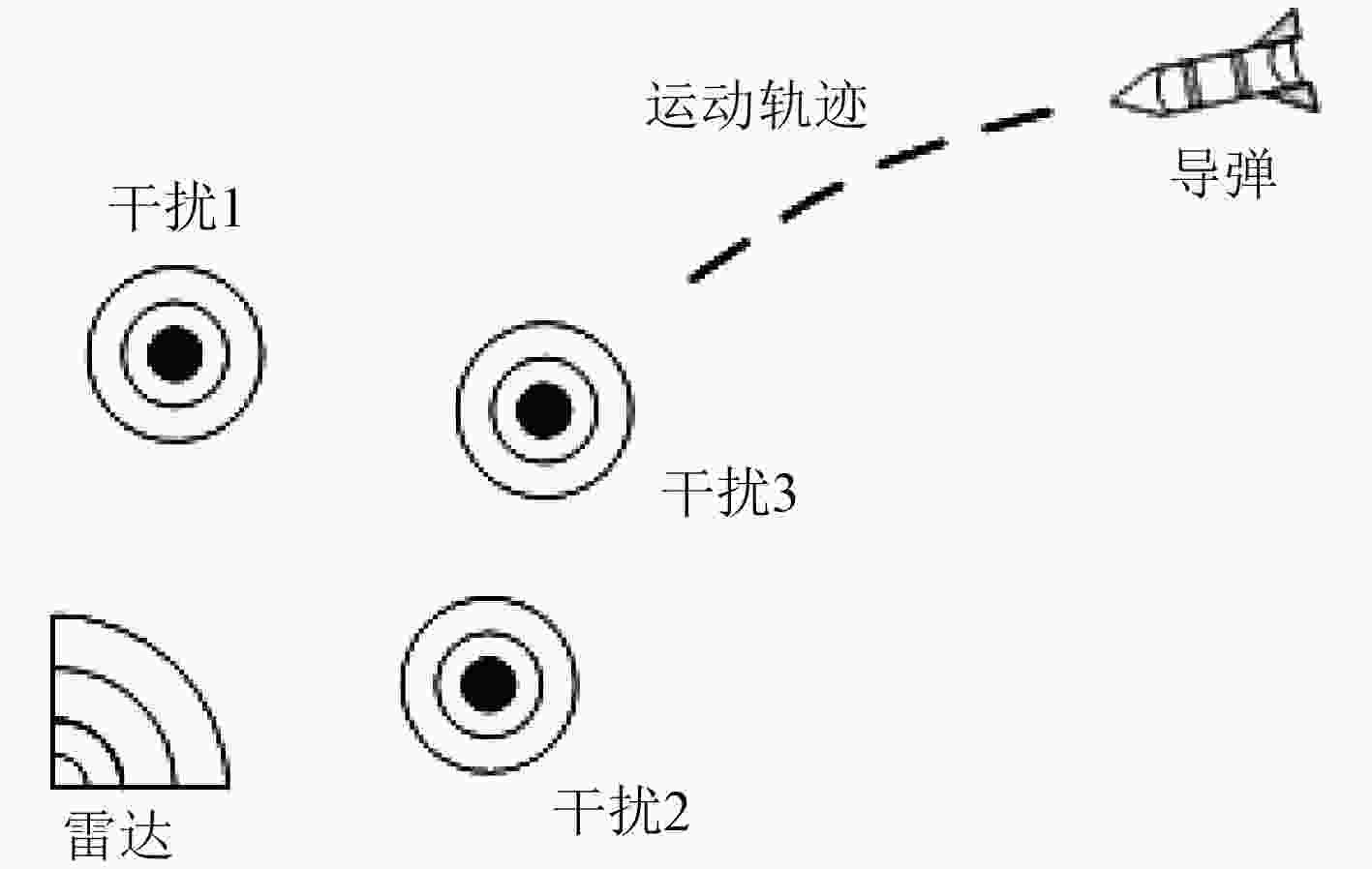
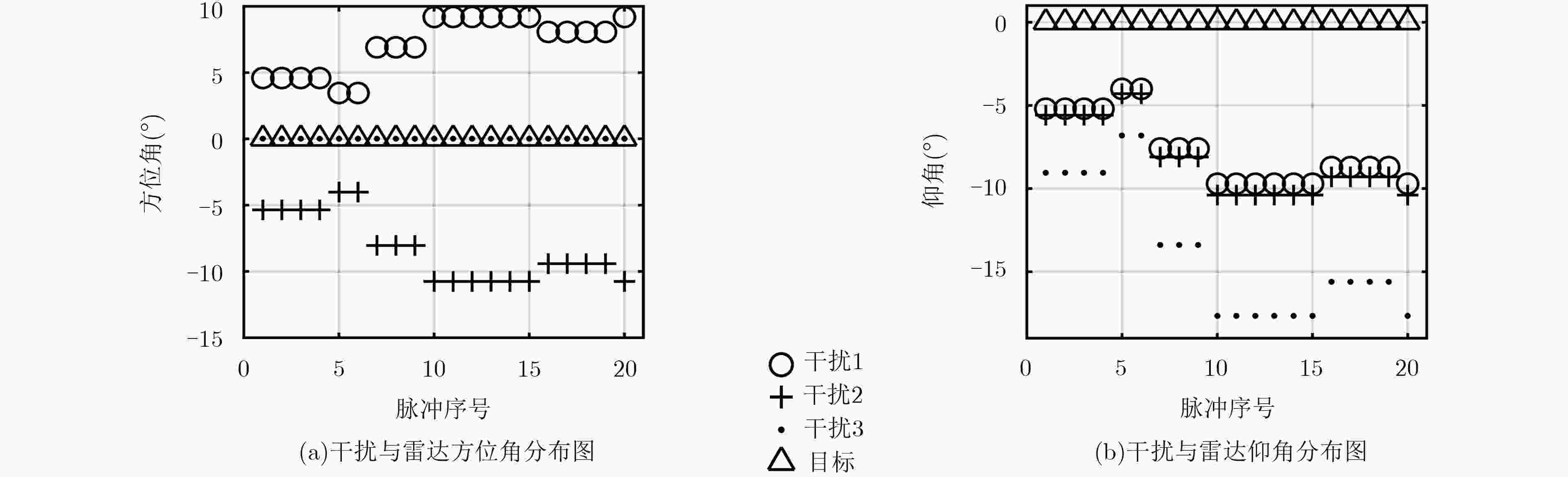
针对有源欺骗干扰环境下基于小样本的DOA估计问题,该文提出自适应极化滤波(APF)联合块稀疏贝叶斯学习(BSBL)算法的DOA估计方法。首先,通过APF抑制干扰能量,提高信干比。然后,建立有源欺骗干扰环境下的稀疏贝叶斯模型,基于相邻快拍相关性,利用BSBL算法进行DOA估计。仿真和实测数据处理结果表明,所提方法降低了干扰对BSBL算法的影响,且与APF联合子空间类算法或最大似然算法(ML)相比,具有更高的空间分辨率和DOA估计精度。
Abstract:For the target DOA estimation under active deception jamming environment with limited samples, a novel DOA estimation method based on the combination of Adaptive Polarization Filter(APF) and Block Sparse Bayesian Learning(BSBL) algorithm is proposed. First, the interference energy is suppressed using APF. Then, the proposed method constructs a sparse Bayesian model under active deception jamming environment. The target DOA is estimated using the BSBL algorithm based on the neighbor time sampling correlation. Simulated and measured data processing results prove that the proposed method reduces the influence of interference on the BSBL algorithm, and has higher spatial resolution and higher angle measurement accuracy, comparing with the method based on the combination of APF and subspace-based DOA algorithms or maximum likelihood DOA algorithm.
-
Key words:
- DOA estimation /
- Anti-jamming /
- Adaptive polarization filter /
- Sparse Bayesian learning
-
ZHOU Chao, LIU Quanhua, and CHEN Xinliang. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 56–63. doi: 10.1049/iet-rsn.2017.0114 LI Zheng, TAI Ning, WANG Chao, et al. A study on blanket noise jamming to LFM pulse compression radar[C]. 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 2017: 1–5. doi: 10.1109/ICSPCC.2017.8242411. WU Xiaohuan, ZHU Weiping, and YAN Jun. A fast gridless covariance matrix reconstruction method for one- and two-dimensional direction-of-arrival estimation[J]. IEEE Sensors Journal, 2017, 17(15): 4916–4927. doi: 10.1109/JSEN.2017.2709329 贾伟娜, 刘顺兰. 模拟退火遗传算法在DOA估计技术中的应用[J]. 计算机工程与应用, 2014, 50(12): 266–270. doi: 10.3778/j.issn.1002-8331.1206-0247JIA Weina and LIU Shunlan. Application of simulated annealing genetic algorithm in DOA estimation technique[J]. Computer Engineering and Applications, 2014, 50(12): 266–270. doi: 10.3778/j.issn.1002-8331.1206-0247 ZHANG T T, LU Y L, and HUI H T. Compensation for the mutual coupling effect in uniform circular arrays for 2D DOA estimations employing the maximum likelihood technique[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1215–1221. doi: 10.1109/TAES.2008.4655375 WAN Liangtian, HAN Guangjie, JIANG Jinfang, et al. DOA estimation for coherently distributed sources considering circular and noncircular signals in massive MIMO systems[J]. IEEE Systems Journal, 2017, 11(1): 41–49. doi: 10.1109/JSYST.2015.2445052 蔡晶晶, 宗汝, 蔡辉. 基于空域平滑稀疏重构的DOA估计算法[J]. 电子与信息学报, 2016, 38(1): 168–173. doi: 10.11999/JEIT150538CAI Jingjing, ZONG Ru, and CAI Hui. DOA estimation via sparse representation of the smoothed array covariance matrix[J]. Journal of Electronics &Information Technology, 2016, 38(1): 168–173. doi: 10.11999/JEIT150538 AL-SHOUKAIRI M, SCHNITER P, and RAO B D. A GAMP-based low complexity sparse Bayesian learning algorithm[J]. IEEE Transactions on Signal Processing, 2018, 66(2): 294–308. doi: 10.1109/TSP.2017.2764855 HOU Huijun and MAO Xingpeng. Oblique projection and sparse reconstruction based DOA estimation of hybrid completely and partially polarized signals with arbitrary polarimetric arrays[C]. Proceedings of the 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, Canada, 2017: 1–4. doi: 10.1109/CCECE.2017.7946799. ZHEN Jiaqi and WANG Zhifang. DOA estimation method for wideband signals by sparse recovery in frequency domain[J]. Journal of Systems Engineering and Electronics, 2017, 28(5): 871–878. doi: 10.21629/JSEE.2017.05.06 WANG Yi, CHEN Baixiao, ZHENG Yisong, et al. Joint power distribution and direction of arrival estimation for wideband signals using sparse Bayesian learning[J]. IET Radar, Sonar & Navigation, 2017, 11(1): 52–59. doi: 10.1049/iet-rsn.2015.0610 王洪雁, 房云飞, 裴炳南. 基于矩阵补全的二阶统计量重构DOA估计方法[J]. 电子与信息学报, 2018, 40(6): 1383–1389. doi: 10.11999/JEIT170826WANG Hongyan, FANG Yunfei, and PEI Bingnan. Matrix completion based second order statistic reconstruction DOA estimation method[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1383–1389. doi: 10.11999/JEIT170826 ZHANG Zhilin and RAO B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912–926. doi: 10.1109/JSTSP.2011.2159773 WANG Lu, ZHAO Lifan, RAHARDJA S, et al. Alternative to extended block sparse Bayesian learning and its relation to pattern-coupled sparse Bayesian learning[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2759–2771. doi: 10.1109/TSP.2018.2816574 HUANG Qinghua, ZHANG Guangfei, and FANG Yong. DOA estimation using block variational sparse Bayesian learning[J]. Chinese Journal of Electronics, 2017, 26(4): 768–772. doi: 10.1049/cje.2017.04.004 宫健, 楼顺天, 张伟涛. 一种强干扰条件下阵列天线波达方向估计方法[J]. 西安电子科技大学学报: 自然科学版, 2018, 45(1): 168–172. doi: 10.3969/j.issn.1001-2400.2018.01.030GONG Jian, LOU Shuntian, and ZAHNG Weitao. Method of array antenna DOA under strong interference presence[J]. Journal of Xidian University, 2018, 45(1): 168–172. doi: 10.3969/j.issn.1001-2400.2018.01.030 MA Jiazhi, SHI Longfei, LI Yongzhen, et al. Angle estimation of extended targets in main-lobe interference with polarization filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 169–189. doi: 10.1109/TAES.2017.2649783 NATHANSON F E. Adaptive circular polarization[C]. IEEE International Radar Conference, Arlington, USA, 1975: 221–225. 王雪松, 汪连栋, 肖顺平, 等. 自适应极化滤波器的理论性能分析[J]. 电子学报, 2004, 32(8): 1326–1329. doi: 10.3321/j.issn:0372-2112.2004.08.023WANG Xuesong, WANG Liandong, XIAO Shunping, et al. Theoretical performance analysis of adaptive polarization filters[J]. Acta Electronica Sinica, 2004, 32(8): 1326–1329. doi: 10.3321/j.issn:0372-2112.2004.08.023 任博, 罗笑冰, 邓方刚, 等. 应用极化聚类中心设计快速自适应极化滤波器[J]. 国防科技大学学报, 2015, 37(4): 87–92. doi: 10.11887/j.cn.201504015REN Bo, LUO Xiaobing, DENG Fanggang, et al. Design of fast adaptive polarization filters utilizing polarizing cluster center[J]. Journal of National University of Defense Technology, 2015, 37(4): 87–92. doi: 10.11887/j.cn.201504015 -





 下载:
下载:


 下载:
下载:
