An Efficient Online Algorithm for Load Balancing in Software Defined Networks Based on Efficiency Range
-
摘要:
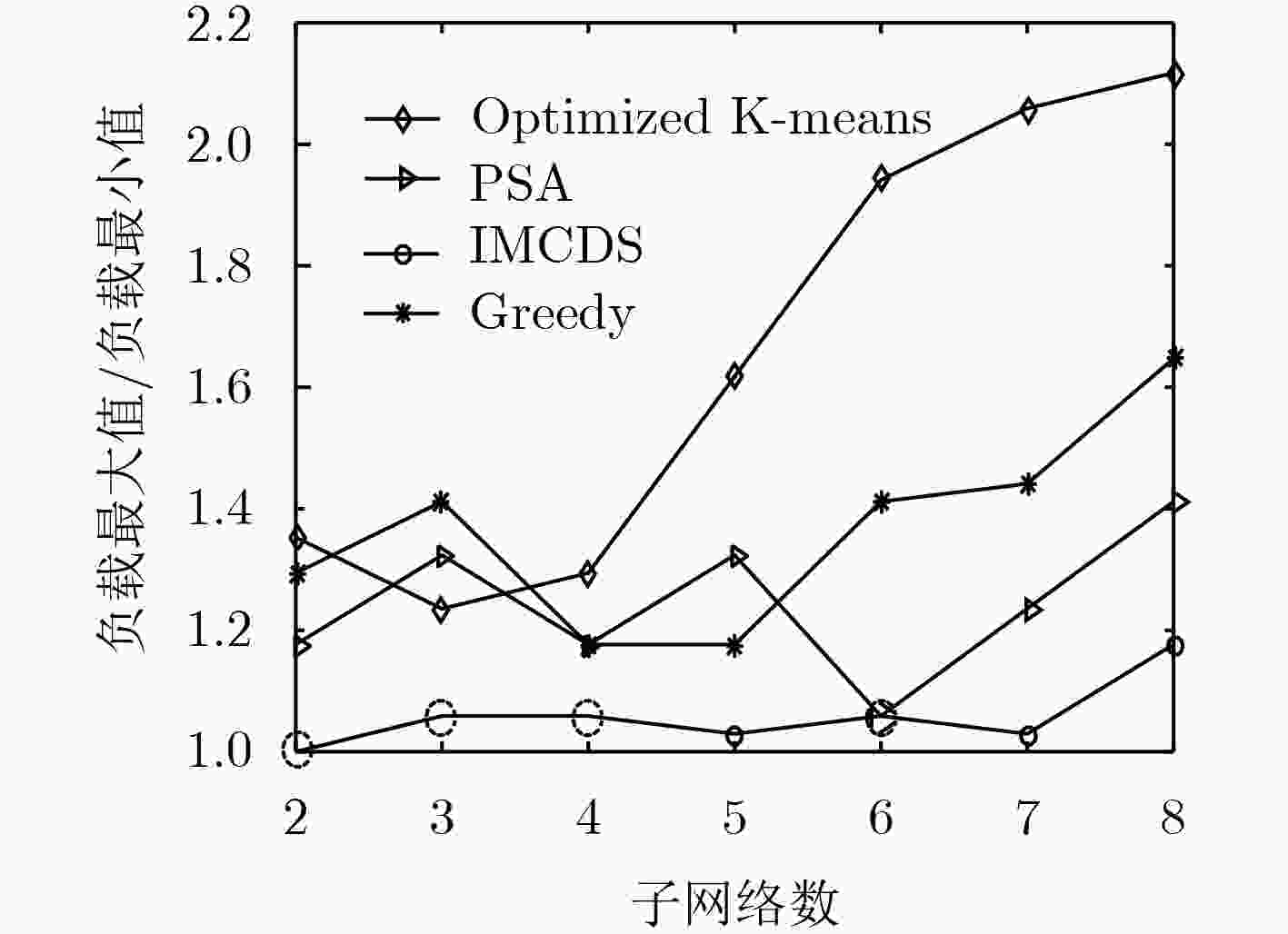
在大型复杂软件定义网络中,为提高网络负载均衡,减少控制器与交换机间的传播时延,该文提出一种基于效率区间的负载均衡在线优化算法。在初始静态网络中,通过贪心算法选择初始控制器集合,并以其为根节点构建M棵改进代价的最小生成树(MST),确定初始M个负载均衡的子网;当网络流量发生变化时,通过广度优先搜索(BFS)调整子网间交换机映射关系使其满足效率区间,保证任意时刻网络的负载均衡。算法均以网络连通性为基础,且均以传播时延为目标重新更新控制器集合。仿真实验表明,该算法在保证任意时刻网络负载均衡的同时,可以保证较低的传播时延,与Pareto模拟退火算法、改进的K-Means算法等相比,可以使网络负载均衡情况平均提高40.65%。
Abstract:Due to the limitation of individual controller’s processing capacity in large-scale complex Software Defined Networks (SDN), an efficient online algorithm for load balancing among controllers based on efficiency range is proposed to improve load balancing among controllers and reduce the propagation delay between a controller and the switch. In the initial static network, the initial set of controllers is selected by a greedy algorithm, then M improved Minimum Spanning Trees (MST) rooted at the initial set of controllers are constructed, so initial M subnets with load balancing are determined. With the dynamic changes of load, for the purpose of making the controller work within efficiency range at any time, several switches in different subnets are reassigned by Breadth First Search (BFS). The initial set of controllers is updated for minimizing propagation delay in the algorithms’ last step. The algorithm is based on the connectivity of intra-domain and inter-domain. Simulation results show that the proposed algorithms not only guarantee the load balancing among controllers, but also guarantee the lower propagation delay. As to compare to PSA algorithm, optimized K-Means algorithm, etc., it can make Network Load Balancing Index (NLBI) averagely increase by 40.65%.
-
表 1 初始M控制域选择算法
算法1:初始M控制域选择算法(IMCDS) 输入:$G = (V, E) , f, {\rm{MLCC}}, {T_{\rm max}}, {W}, D, {\rm{ID}}, $
$ \{ {\rm{Flag}}, {\rm{Temp}}, {\rm{ICon}}, {\rm{IS}}\} = \varnothing $输出:${\rm{ICon}}, {\rm{IS}}$ (1) $M \leftarrow {{\displaystyle\sum\nolimits_{i = 1}^{\left| V \,\right|} {{f_i}} }}\Bigr/{{\rm{OL}}} , {\rm{OL}} = 0.85 \times {\rm{MLCC}}$; (2) ${\rm{ICon}} \leftarrow {C_1}, {C_1} \in \{ \max (D) \cap \max ({\rm{ID}})\} $; (3) Adopt $ { \rm{Prim}} ({C_1}, {W}, {\rm{OL}}) $ to construct first improved MST
based 式(11) and 式(12);(4) Update $ {\rm{IS}}_1, {\rm{Flag}}_1 \leftarrow 1, {\rm{Temp}} \leftarrow 1$; (5) do (6) ${\rm{ICon}} \leftarrow {C_i}, {C_i} \in \{ {\rm{Flag}}_i = 0 \cap {\rm{furthest \;from\;}} {\rm{ICon}} \cap $
$ \max (D) \cap \max ({\rm{ID}}),i = 1, ·\!·\!· , n\} $;(7) Adopt $ { \rm{Prim}} ({C_i}, {W}, {\rm{OL}}) $ to construct improved MST
based on 式(11) and 式(12);(8) Update $ {\rm{IS}}_i, {\rm{Flag}}_i \leftarrow 1, {\rm{Temp}} \leftarrow {\rm{Temp}} + 1$; (9) while $ {\rm{Temp}} > M, {\rm{the \ network \ has \ been \ divided \ into}} \ $ M
domains;(10) if there are nodes has not been selected do (11) Add nodes to one closest improved MST by BFS based
on 式(11) and 式(12);(12) Update ${\rm{IS}} , {\rm{Flag}} \leftarrow 1$; (13) end if (14) Update centroids ${\rm{ICon}} = \{ {C_1}, {C_2}, ·\!·\!· , {C_M}\} $ based on the
sum of the shortest distance from all switches in ${\rm{IS}} _i $ to
new controller $ {C_i}$ is minimized;(15) Output ${\rm{ICon}} , {\rm{IS}}$。 表 2 M控制域调整算法
算法2:M控制域调整算法(M-CDA) 输入:$G = (V, E), {T_{\max}}, f, {\rm{MLCC}}, (\alpha , \beta ), {\rm{ICon}}, {\rm IS}, T, $
$ \{ {\rm{LS}}, {\rm{LCon}}, {\rm{TNS}}\} = \varnothing $输出:${\rm{LCon}}, {\rm{LS}}$ (1) for all $ {\rm{}} t\; {\rm{with}} \;0 \le t \le T\; $ do (2) for each $ i \in M $ do (3) ${\rm{TNS}} \leftarrow {\rm{BV}}_{i, j}, {\rm{BV}}_{i, j} \in \{ {\rm{furthest}} \;{\rm{from}} \; $
$ {\rm{ICon}}_i \cap\max \left(f_{i1}^t, ·\!·\!· ,f_{ij}^t\right) ,j \in {\rm{IS}}_i\} $;(4) end for (5) for each $ i \in M $ do (6) if $\sum\nolimits_{l = t - 1}^t {\rm{L C}}_i^l < \alpha \times {\rm{MLCC}} $ do (7) Add nodes in TNS closest from $ {\rm{ICon}}_i$ to ISi by BFS
based 式(11),式(12),式(13);(8) end if (9) if $\sum\nolimits_{l = t - 1}^t {\rm{L C}}_i^l > \beta \times {\rm{MLCC}} $ do (10) Add nodes in ISi furthest from ${\rm{ICon}}_i$ to TNS by BFS
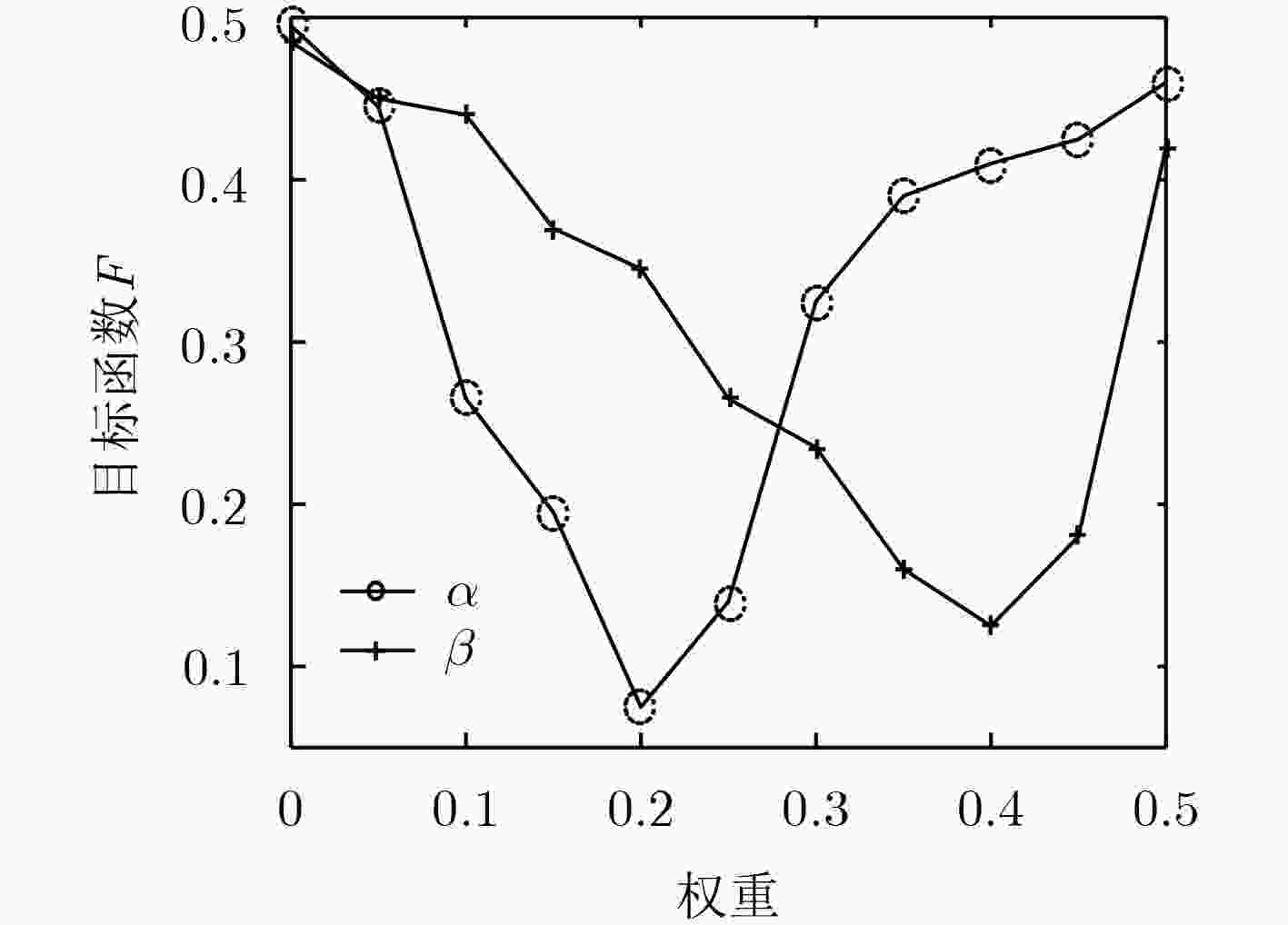
based 式(11),式(12),式(13);(11) end if (12) end for (13) Compute function
${\rm{ }} {F_t} = \mu \times ({\rm{NLBI}}^t - 1) + \nu \times \sum\limits_{j = 1}^M {{\rm{TRDT}}_j^t} $(14) if ${F_t} < {F_{t - 1}} $ do (15) ${\rm{LS}} \leftarrow {\rm{IS}}$; (16) end if (17) end for (18) Update centroids $ {\rm{ICon}} = \{ {C_1}, {C_2}, ·\!·\!· , {C_M}\} $ based on the
sum of the shortest distance from all switches in ${\rm{}} {\rm{LS}}_i $ to
new controller Ci is minimized, ${\rm{LCon}} \leftarrow {\rm{ICon}}$;(19) Output $ {\rm{LCon}}, {\rm{LS}}$。 表 3 网络拓扑节点数和链路数分布
网络名称 Noel Darkstrand OS3E Arnes Ntelos Surfnet 节点数 19 28 34 34 48 50 链路数 35 31 43 49 61 73 表 4 初始静态情况下多网络拓扑的负载均衡情况
子网络数 Noel Darkstrand OS3E Arnes Ntelos Surfnet 2 1.05 1.00 1.00 1.00 1.00 1.00 3 1.10 1.07 1.06 1.06 1.00 1.02 4 1.26 1.14 1.06 1.06 1.08 1.04 5 1.05 1.07 1.03 1.18 1.25 1.20 6 1.26 1.06 1.06 1.06 1.13 1.08 7 1.48 1.25 1.03 1.23 1.17 1.12 8 1.52 1.43 1.18 1.41 1.17 1.12 表 5 动态情况下多网络拓扑的负载均衡情况
子网络数 Noel Darkstrand OS3E Arnes Ntelos Surfnet 2 1.08 1.04 1.02 1.04 1.03 1.05 3 1.09 1.10 1.08 1.11 1.06 1.03 4 1.18 1.23 1.12 1.16 1.08 1.09 5 1.20 1.25 1.13 1.23 1.18 1.15 6 1.34 1.28 1.26 1.28 1.12 1.31 7 1.41 1.33 1.38 1.36 1.33 1.24 8 1.51 1.48 1.26 1.34 1.23 1.18 -
HLLER B, SHEERWOOD R, and MCKEOWN N. The controller placement problem[J]. ACM Sigcomm Computer Communication Review, 2012, 42(4): 473–478. doi: 10.1145/2377677.2377767 KOPONEN T, CASADO M, GUDE N, et al. Onix: A distributed control platform for large-scale production networks[C]. Usenix Conference on Operating Systems Design and Implementation, Vancouver, Canada, 2010: 351–364. TOOTOONCHIAN A and GANJALI Y. HyperFlow: A distributed control plane for OpenFlow[C]. Internet Network Management Conference on Research on Enterprise Networking, San Francisco, USA, 2010: 3–8. YU M, REXDORD J, FREEDMAN M J, et al. Scalable flow-based networking with DIFANE[J]. ACM Sigcomm Computer Communication Review, 2010, 40(4): 351–362. doi: 10.1145/1851275.1851224 WANG Guodong, ZHAO Yanxiao, HUANG Jun, et al. A K-means-based network partition algorithm for controller placement in software defined network[C]. IEEE International Conference on Communicat–uala Lumpur, Malaysia, 2016: 1–6. 张栋, 郭俊杰, 吴春明. 层次型多中心的SDN控制器部署[J]. 电子学报, 2017, 45(3): 680–686. doi: 10.3969/j.issn.0372-2112.2017.03.027ZHANG Dong, GUO Junjie, and WU Chunming. Controller placement based on hierarchical multi-center SDN[J]. Acta Electronica Sinica, 2017, 45(3): 680–686. doi: 10.3969/j.issn.0372-2112.2017.03.027 SAHOO K S, SAHOO B, DASH R, et al. Optimal controller selection in software defined network using a greedy-SA algorithm[C]. International Conference on Computing for Sustainable Global Development, New Delhi, India, 2016: 2342–2346. YAO Guang, BI Jun, LI Yuliang, et al. On the capacitated controller placement problem in software defined networks[J]. IEEE Communications Letters, 2014, 18(8): 1339–1342. doi: 10.1109/LCOMM.2014.2332341 SALLAHI A and ST-HILAIRE M. Optimal model for the controller placement problem in software defined networks[J]. IEEE Communications Letters, 2015, 19(1): 30–33. doi: 10.1109/LCOMM.2014.2371014 JIMENEZ Y, CERVALLO-PASTOR C, and GARCIA A J. On the controller placement for designing a distributed SDN control layer[C]. NETWORKING Conference, Trondheim, Norway, 2014: 1–9. LANGE S, GEBERT S, ZINNER T, et al. Heuristic approaches to the controller placement problem in large scale SDN networks[J]. IEEE Transactions on Network & Service Management, 2015, 12(1): 4–17. doi: 10.1109/TNSM.2015.2402432 JALILI A, AHMADI V, KESHTGARI M, et al. Controller placement in software-defined WAN using multi objective genetic algorithm[C]. International Conference on Knowledge-Based Engineering and Innovation, Tehran, Iran, 2016: 656–662. RATH H K, REVVOORI V, NADAF S M, et al. Optimal controller placement in software defined networks (SDN) using a non-zero-sum game[C]. International Symposium on A World of Wireless, Mobile and Multimedia Networks, Sydney, Australia, 2014: 1–6. 史久根, 邾伟. 软件定义网络中基于负载均衡的多控制器部署算法[J]. 电子与信息学报, 2018, 40(2): 455–461. doi: 10.11999/JEIT170464SHI Jiugen and ZHU Wei. Multi-controller deployment algorithm based on load balance in software defined network[J]. Journal of Electronics &Information Technology, 2018, 40(2): 455–461. doi: 10.11999/JEIT170464 WANG Tao, LIU Fangming, and XU Hong. An efficient online algorithm for dynamic SDN controller assignment in data center networks[J]. IEEE/ACM Transactions on Networking, 2017, 25(5): 2788–2801. doi: 10.1109/TNET.2017.2711641 覃匡宇, 黄传河, 王才华, 等. SDN网络中受时延和容量限制的多控制器均衡部署[J]. 通信学报, 2016, 37(11): 90–103. doi: 10.11959/j.issn.1000-436x.2016219QIN Kuangyu, HUANG Chuanhe, WANG Caihua, et al. Balanced multiple controllers placement with latency and capacity bound in software-defined network[J]. Journal on Communications, 2016, 37(11): 90–103. doi: 10.11959/j.issn.1000-436x.2016219 -





 下载:
下载:


 下载:
下载:
