Time of Arrival Estimation Based on Sparse Reconstruction Loop Matching Pursuit Algorithm
-
摘要:
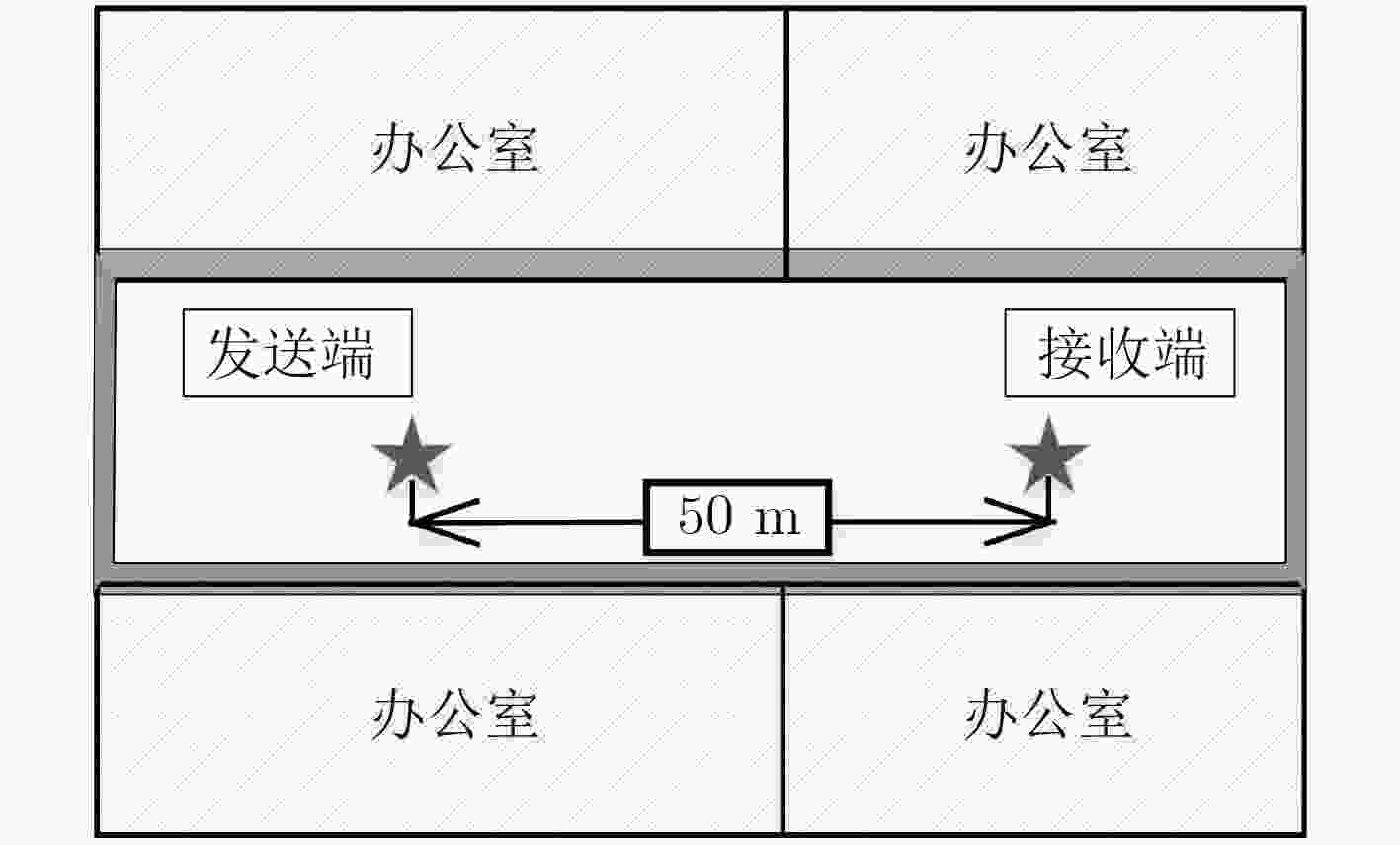
在单样本(SMV)、低信噪比条件下,稀疏重构方法可提升时延估计精度,但现有的重构算法在支撑集元素的选择中存在错选和漏选的情况,从而导致估计精度受限。针对上述问题,该文提出一种基于循环匹配追踪(LMP)的稀疏重构时延估计算法。该方法引入了“循环删除,匹配添加”的思想,有效提升了直达径的估计精度。算法首先建立信道冲激响应稀疏表示模型;然后在获得初始支撑集的前提下,先循环删除支撑集内的元素,再从支撑集补集中依据与当前残差内积值最大来匹配添加新元素,直至残差内积基本不变;最后利用时延值与稀疏支撑集的关系得到了时延的估计值。仿真结果表明,所提算法相比于传统稀疏重构时延估计算法具有更高的估计精度。同时基于USRP平台,利用实际信号对所提算法进行了有效性验证。
Abstract:Under Single Measurement Vector (SMV) and low Signal-to-Noise Ratio (SNR) conditions, the sparse reconstruction method can improve the estimation accuracy of Time Of Arrival (TOA). However, the existing reconstruction algorithms have some mistakes and missing in the selection of sparse support set elements, which leads to limited estimation accuracy. In order to solve this problem, this paper proposes an algorithm based on sparse reconstruction Loop Matching Pursuit (LMP), which improves the estimation accuracy of the direct path. The algorithm first establishes a sparse representation model of channel impulse response. Then, under the premise of having obtained initial support set, the elements in the support set are removed cyclically. In addition, according to the maximum value of the current residual within the product, the remaining elements are used to match and add the new elements until the residual product is the same. Finally, the estimate of the TOA is obtained using the relationship between the time delay value and the sparse support set. The simulation results show that the proposed algorithm has higher estimation accuracy than the traditional sparse reconstruction time delay estimation algorithm. At the same time, based on the USRP platform, the effectiveness of the proposed algorithm is verified by the actual signal.
-
表 1 OFDM系统参数设置
参数 数值 FFT周期${T_{{\rm{FFT}}}}$ 3.2 μs 系统带宽$B$ 20 MHz 子载波数 64个 载波频率${f_c}$ 2.4 GHz 表 2 计算复杂度对比
算法 复杂度 Root-Music $O\left( {{M^3}{\rm{ + 2}}{{\rm{M}}^2}{\rm{ + }}5M{\rm{ - }}LM} \right)$ OMP $O\left( {{M^2}{L^2} + MNL} \right)$ LMP $O\left( {2{M^2}{L^2} + 2MNL} \right)$ CoSaMP $O\left( {3{M^2}{L^2} + MNL} \right)$ NS $O\left( {{N^2} + ({M^2} + {L^2})N} \right)$ 表 3 5种算法多径估计结果比较
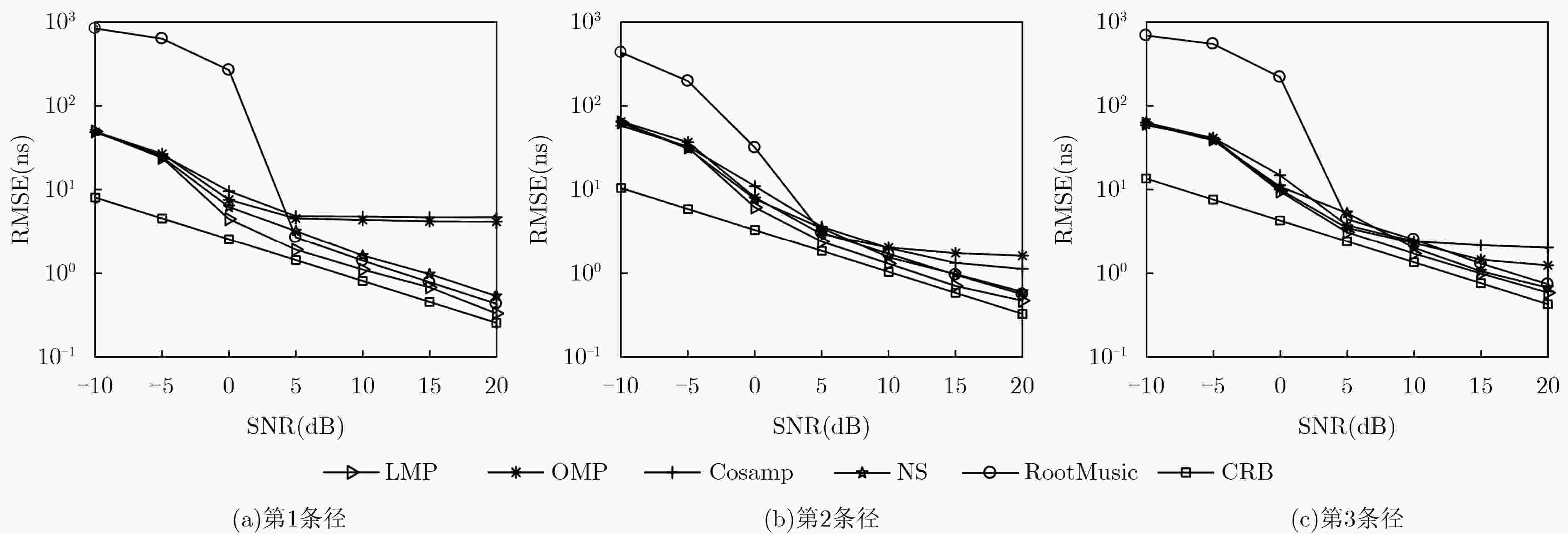
算法 第1条径 第2条径 第3条径 估计均值(m) 标准差 RMSE 估计均值(m) 标准差 估计均值(m) 标准差 LMP 50.0100 0.3015 0.3017 57.0900 0.3803 62.7900 0.3562 OMP 48.9000 1.4387 1.8111 56.8400 2.2037 61.5600 1.3537 CoSaMP 47.5500 2.5989 3.5717 58.4800 1.4648 59.8200 1.3563 NS 49.7600 0.6556 0.6742 55.8900 2.3162 60.5100 1.1623 Root-Music 49.8250 0.7915 0.7925 57.6600 0.9468 62.2200 0.9119 -
CHEON J, HWANG H, KIM D, et al. IEEE 802.15.4 Zigbee-based time-of-arrival estimation for wireless sensor networks[J]. Sensors, 2016, 16(2): 203. doi: 10.3390/s16020203 LI Xinya, DENG Zhiqun, RAUCHENSTEIN L T, et al. Contributed review: Source-localization algorithms and applications using time of arrival and time difference of arrival measurements[J]. Review of Scientific Instruments, 2016, 87(4): 921–960. doi: 10.1063/1.4947001 ANASTOPOULOS C and SAVVIDOU N. Time-of-arrival correlations[J]. Physical Review A, 2017, 95(3): 100–105. doi: 10.1103/PhysRevA.95.032105 AN S P, HU T Y, CUI Y F, et al. Cumulant-based time delay estimations based solution for statics correction of land data[C]. 79th EAGE Conference and Exhibition. Paris, France, 2017: 1–3. CHENG Lin, CHEN Gang, GAO Wenzhong, et al. Adaptive time delay compensator (ATDC) design for wide-area power system stabilizer[J]. IEEE Transactions on Smart Grid, 2014, 5(6): 2957–2966. doi: 10.1109/TSG.2014.2347401 CHLMPAGNE B, EIZENMAN M, and PASUPATHY S. Exact maximum likelihood time delay estimation[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Washington, D.C., USA, 1991: 2633–2636. 李雪梅, 陶然, 王越. 时延估计技术研究[J]. 雷达科学与技术, 2010, 8(4): 362–371. doi: 10.3969/j.issn.1672-2337.2010.04.015LI Xuemei, TAO Ran, and WANG Yue. Research on time delay estimation technology[J]. Radar Science and Technology, 2010, 8(4): 362–371. doi: 10.3969/j.issn.1672-2337.2010.04.015 DOGAN M C, and MENDEL J M. Applications of cumulants to array processing. I. aperture extension and array calibration[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1200–1216. doi: 10.1109/78.382404 HÄCKER P and YANG B. Single snapshot DOA estimation[J]. Advances in Radio Science, 2010, 8(2): 251–256. doi: 10.5194/ars-8-251-2010 WANG Fangqiu and ZHANG Xiaofei. Joint estimation of TOA and DOA in IR-UWB system using sparse representation framework[J]. Etri Journal, 2014, 36(3): 460–468. doi: 10.4218/etrij.14.0113.0555 冷雪冬, 巴斌, 逯志宇, 等. 基于回溯筛选的稀疏重构时延估计算法[J]. 物理学报, 2016, 65(21): 88–96. doi: 10.7498/aps.65.210701LENG Xuedong, BA Bin, LU Zhiyu, et al. Backtracking-based sparse reconstruction delay estimation algorithm[J]. Acta Physica Sinica, 2016, 65(21): 88–96. doi: 10.7498/aps.65.210701 NAFIE M, TEWFIK A H, ALI M, et al. Deterministic and iterative solutions to subset selection problems[J]. IEEE Transactions on Signal Processing, 2002(7): 1591–1601. doi: 10.1109/tsp.2002.1011200 李智勇. 基于压缩感知的脉冲超宽带系统窄带干扰抑制问题研究[D]. [博士论文], 山东大学, 2014: 17–21.LI Zhiyong. Research on narrowband interference suppression in pulsed ultra-wideband systems based on Compressed Sensing[D]. [Ph.D. dissertation], Shandong University, 2014: 17–21. 张宏洲. 稀疏场景合成孔径雷达图像压缩研究[D]. [博士论文], 上海交通大学, 2010: 13–15.ZHANG Hongzhou. Research on image compression of sparse scene synthetic aperture radar[D]. [Ph.D. dissertation], Shanghai Jiao Tong University, 2010: 13–15. 胡南. 基于稀疏重构的阵列信号波达方向估计算法研究[D]. [博士论文], 中国科学技术大学, 2013: 20–26.HU Nan. Research on direction of arrival estimation of array signals based on sparse reconstruction[D]. [Ph.D. dissertation], University of Science and Technology of China, 2013: 20–26. 王方秋, 张小飞, 汪飞. IR-UWB系统中基于root-MUSIC算法的TOA和DOA联合估计[J]. 通信学报, 2014, 35(2): 137–145. doi: 10.3969/j.issn.1000-436x.2014.02.018WANG Fangqiu, ZHANG Xiaofei, and WANG Fei. Joint estimation of TOA and DOA based on Root-MUSIC algorithm in IR-UWB system[J]. Journal of Communications, 2014, 35(2): 137–145. doi: 10.3969/j.issn.1000-436x.2014.02.018 巴斌, 郑娜娥, 朱世磊, 等. 利用蒙特卡罗的最大似然时延估计算法[J]. 西安交通大学学报, 2015, 49(8): 24–30. doi: 10.7652/xjtuxb201508005BA Bin, ZHENG Nae, ZHU Shilei, et al. A maximum likelihood time delay estimation algorithm using Monte Carlo method[J]. Journal of Xi’an Jiaotong University, 2015, 49(8): 24–30. doi: 10.7652/xjtuxb201508005 MATTBEWS. GAST. Definitive Guide to 802.11 Wireless Networks[M]. Nanjing: Southeast University Press, 2007: 293–297. -






 下载:
下载:
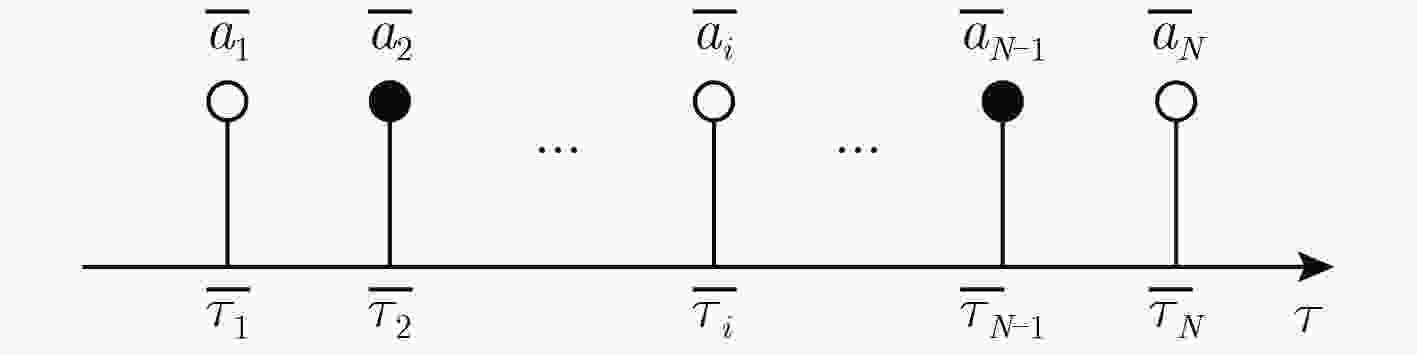
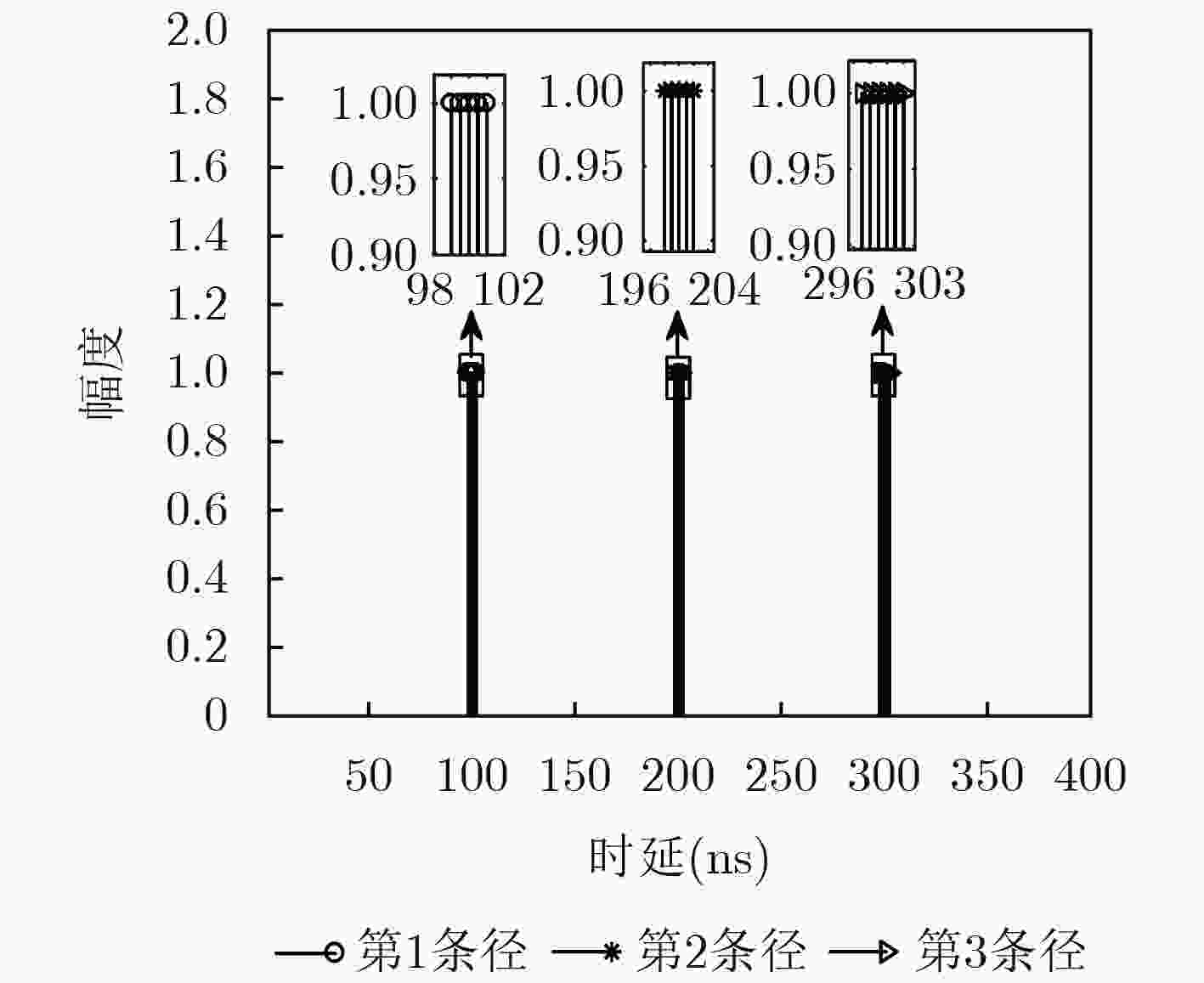
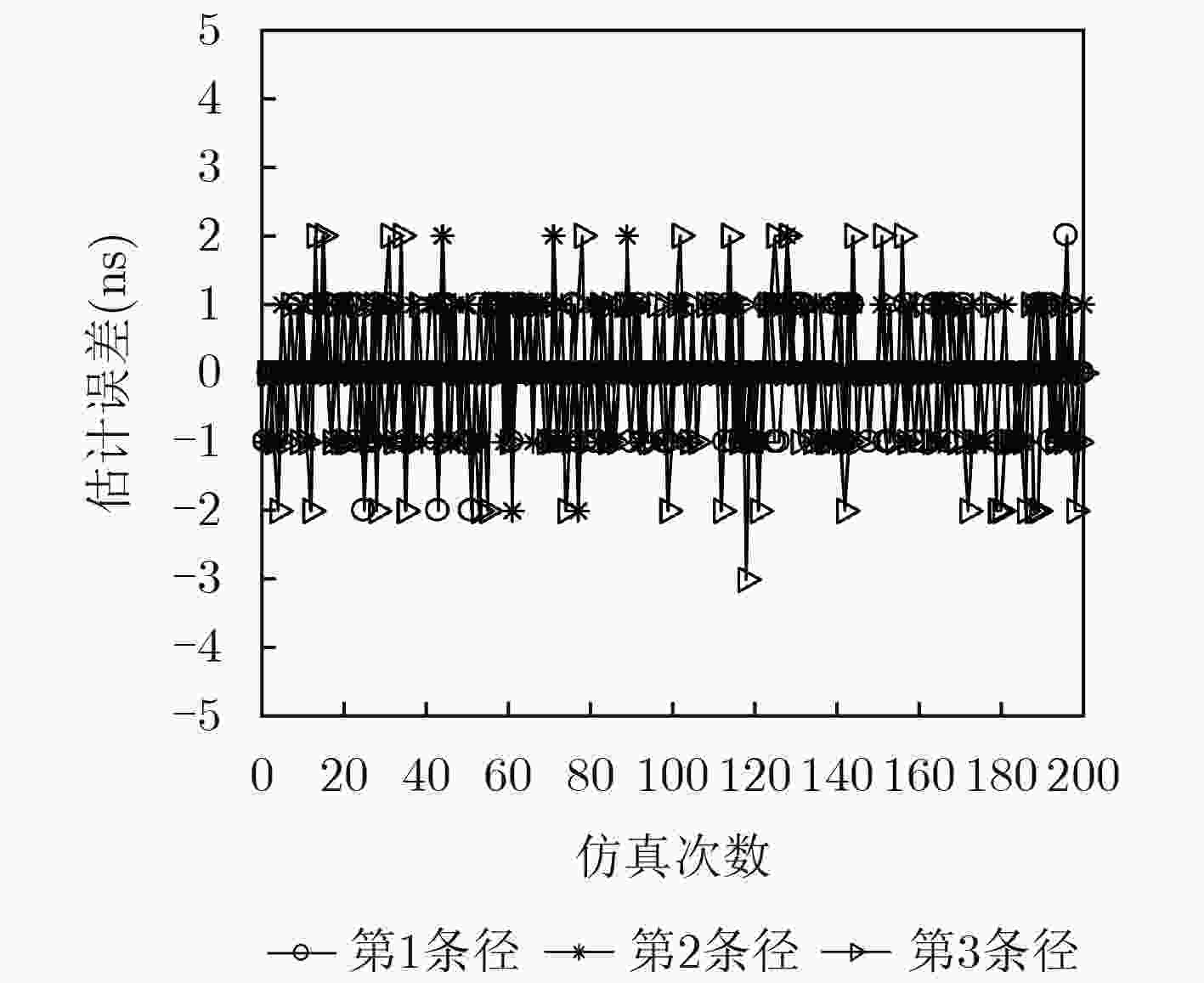
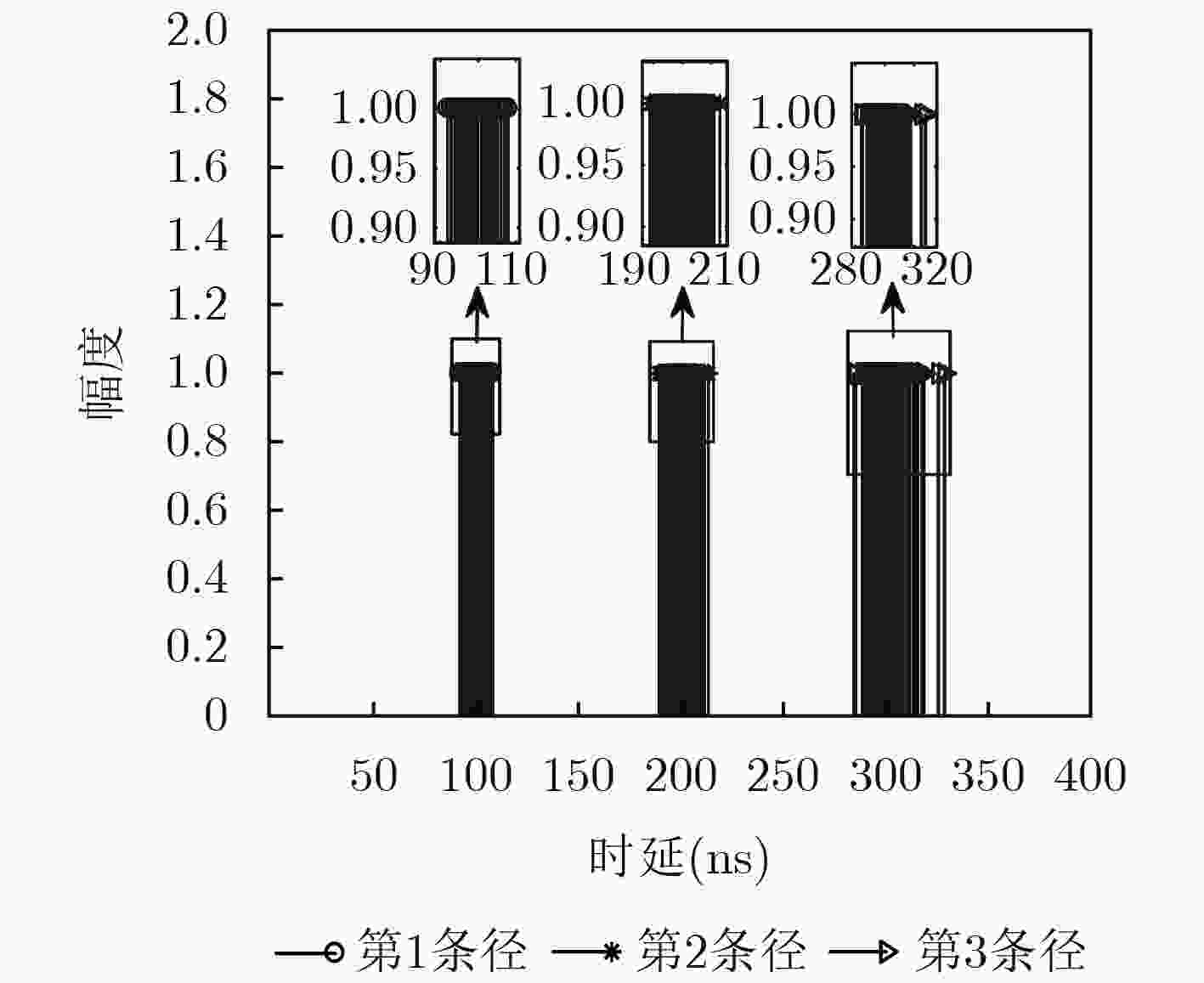


 下载:
下载:
