Hybrid Point of Interest Recommendation Algorithm Based on Deep Learning
-
摘要:
针对现有兴趣点推荐的初始化和忽视评论信息语义上下文信息的问题,将深度学习融入推荐系统中已经成为兴趣点推荐研究的热点之一。该文提出一种基于深度学习的混合兴趣点推荐模型(MFM-HNN)。该模型基于神经网络融合评论信息与用户签到信息来提高兴趣点推荐的性能。具体地,利用卷积神经网络学习评论信息的特征表示,利用降噪自动编码对用户签到信息进行初始化。进而,基于扩展的矩阵分解模型融合评论信息特征和用户签到信息的初始值进行兴趣点推荐。在真实签到数据集上进行实验,结果表明所提MFM-HNN模型相比其他先进的兴趣点推荐具有更好的推荐性能。
Abstract:When modeling user preferences, the current researches of recommendation ignore the problem of modeling initialization and the review information accompanied with rating information for recommender models, integrating deep learning into the recommendation system becomes a hotspot of Point-Of-Interest (POI) recommendation. In this paper, a new POI recommendation model called Matrix Factorization Model integrated with Hybrid Neural Networks (MFM-HNN) is proposed. The model improves the performance of POI recommendation by fusing review text and check-in information based on Neural Network (NN). Specifically, the convolutional neural network is used to learn the feature representation of the review text and the check-in information is initialized by using the stacked denoising autoencoder. Furthermore, the extended matrix factorization model is exploited to fuse the review information feature and the initial value of the check-in information for POI recommendation. As is shown in the experimental results on real datasets, the proposed MFM-HNN achieves better recommendation performances than the other state-of-the-art POI recommendation algorithms.
-
表 1 MFM-HNN模型学习算法
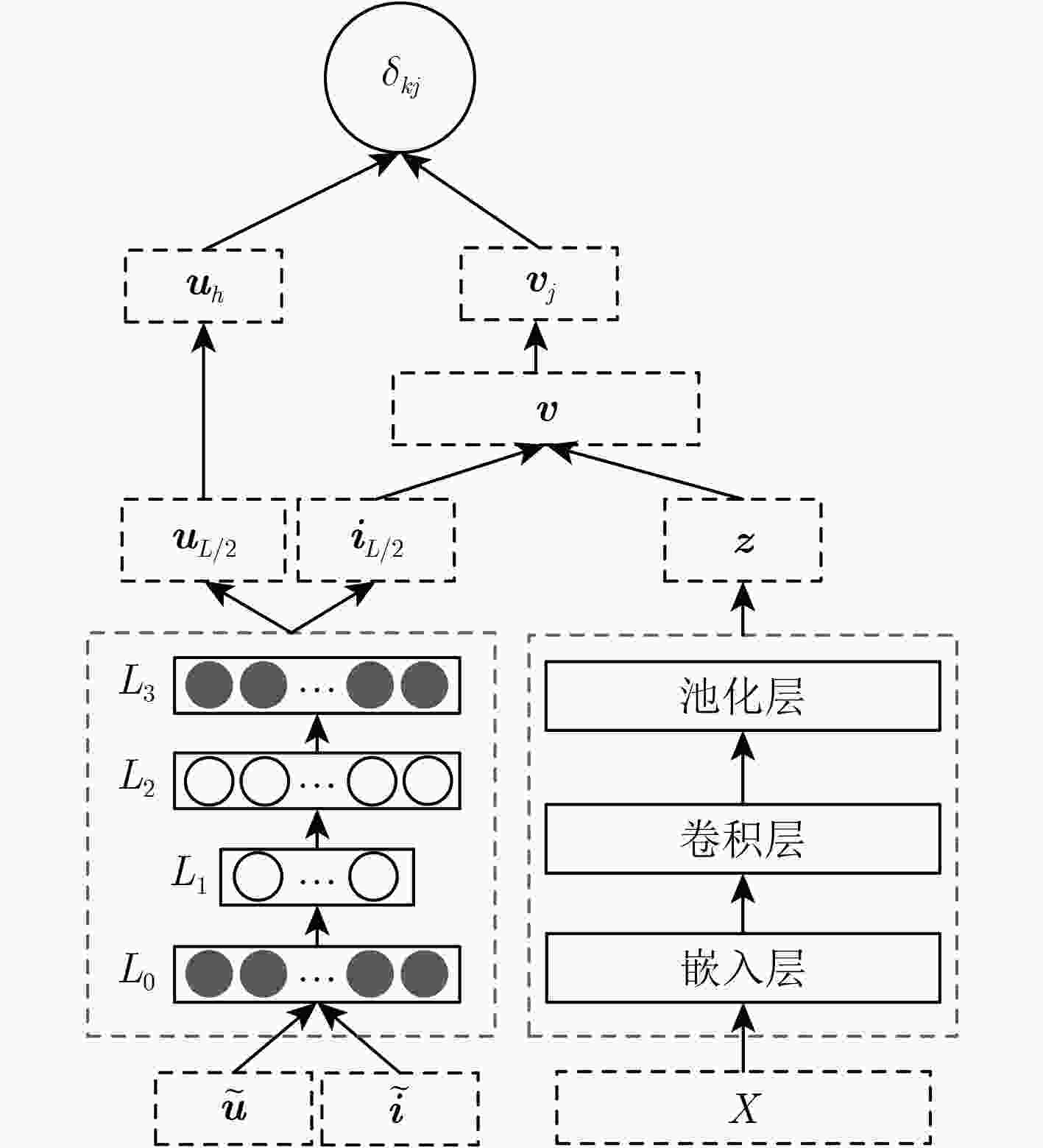
输入:${{{x}}_i},{{{S}}^u},{{{S}}^v},{{\tilde{{S}}}^u},{{\tilde{{S}}}^v},T,B$ 输出:${\cal{L}}$ (1) For $t < $T Do (2) 从兴趣点评论中随机选取一个兴趣点的评论矩阵${{{x}}_i}$进行训练, 训练批次大小为${\beta _0}$,每一个批次的大小为$B$,计算训练过程 中的损失${{\cal{L}}_{\rm{cnn}}}$ (3) if $t > $T or ${{\cal{L}}_{\rm{cnn}}}$足够小 (4) end (5) for $t < $T Do (6) 从兴趣点评分中随机选取一个兴趣点的用户-兴趣点对$({\tilde{{s}}}_i^u,{\tilde{{s}}}_i^v)$ 进行训练,训练批次大小为${\beta _1}$,每一个批次的大小为$B$,计算 训练过程中的损失${{\cal{L}}_{\rm{ui}}}$ (7) if $t > $T or ${{\cal{L}}_{\rm{ui}}}$足够小 (8) end (9) 计算最终的损失值${\cal{L}} = {{\cal{L}}_{\rm{cnn}}} + {{\cal{L}}_{\rm{ui}}}$ (10) return ${\cal{L}}$ 表 2 数据集统计
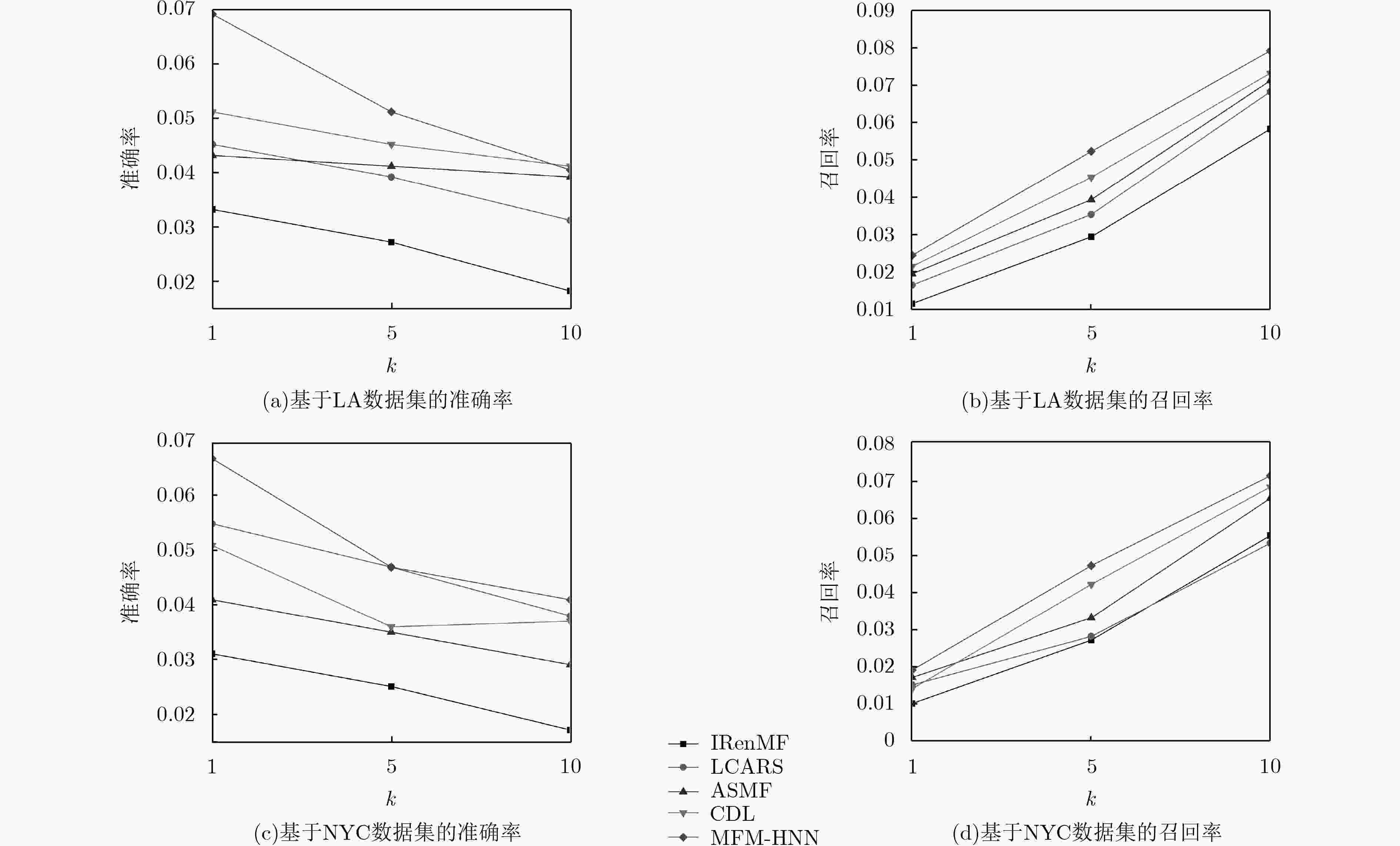
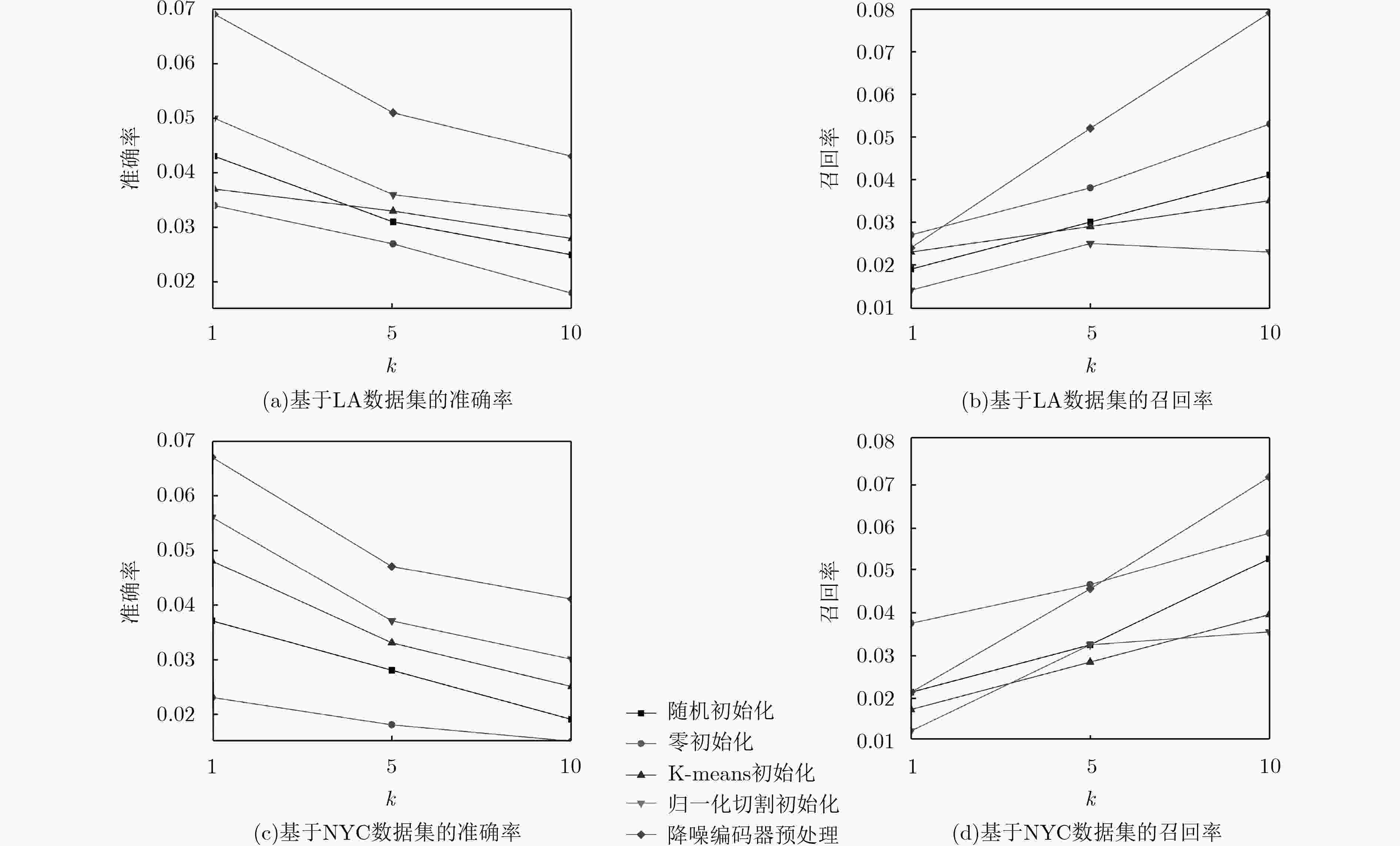
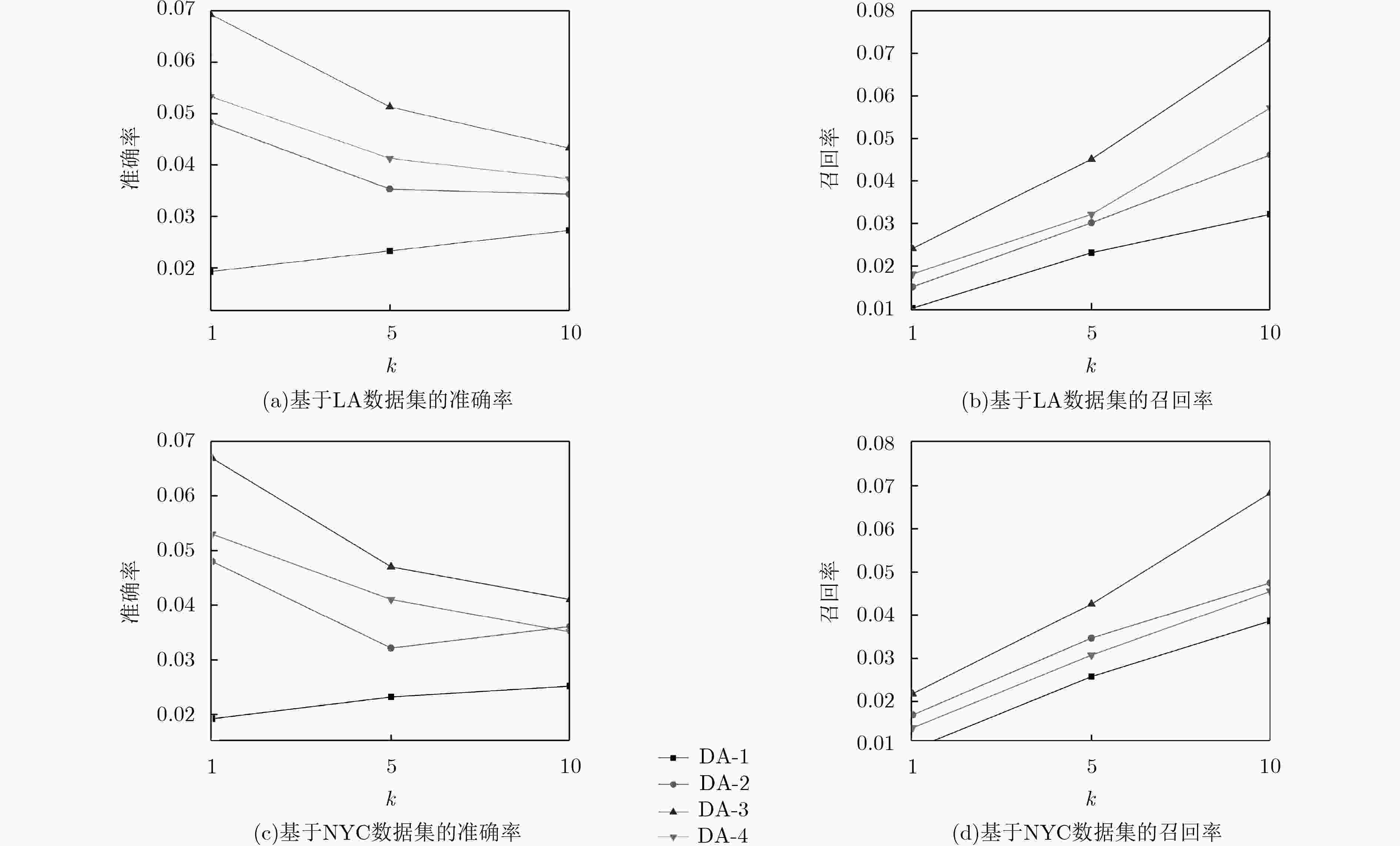
数据统计 LA NYC 用户数量 30,208 47,240 兴趣点数量 142,798 203,765 签到数量(评论) 244,861 388,954 用户-位置矩阵密度 5.68×10–5 4.04×10–5 -
LI Jun, BENEDIKTSSON J A, ZHANG Bing, et al. Spatial technology and social media in remote sensing: A survey[J]. Proceedings of the IEEE, 2017, 105(10): 1855–1864 doi: 10.1109/JPROC.2017.2729890 YANG, C, BAI Lanxiao, ZHANG Chao, et al. Bridging collaborative filtering and semi-supervised learning: A neural approach for POI recommendation[C]. Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, Canada, 2017: 1245–1254. LIU Yiding, PHAM T A N, CONG Gao, et al. An experimental evaluation of point-of-interest recommendation in location-based social networks[J]. Proceedings of the VLDB Endowment, 2017, 10(10): 1010–1021 doi: 10.14778/3115404.3115407 MAZUMDAR P, PATRA B K, BABU K S, et al. Hidden location prediction using check-in patterns in location-based social networks[J]. Knowledge and Information Systems, 2017, 57(3): 571–601 doi: 10.1007/s10115-018-1170-5 余永红, 高阳, 王皓. 基于Ranking的泊松矩阵分解兴趣点推荐算法[J]. 计算机研究与发展, 2016, 53(8): 1651–1663 doi: 10.7544/issn1000-1239.2016.20160202YU Yonghong, GAO Yang, and WANG Hao. A ranking based Poisson matrix factorization model for point-of-interest recommendation[J]. Journal of Computer Research and Development, 2016, 53(8): 1651–1663 doi: 10.7544/issn1000-1239.2016.20160202 LIM K H, CHAN J, LECKIE C, et al. Personalized trip recommendation for tourists based on user interests, points of interest visit durations and visit recency[J]. Knowledge and Information Systems, 2018, 54(2): 375–406 doi: 10.1007/s10115-017-1056-y YIN Hongzhi, SUN Yizhou, CUI Bin, et al. LCARS: A location-content-aware recommender system[C]. Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, USA, 2013: 221–229. ZHANG Jiadong, CHOW Chiyin, and ZHENG Yu. ORec: An opinion-based point-of-interest recommendation framework[C]. Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, Melbourne, Australia, 2015: 1641–1650. WANG Hao, WANG Naiyan, and YEUNG D Y. Collaborative deep learning for recommender systems[C]. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 2015: 1235–1244. KIM D, PARK C, OH J, et al. Convolutional matrix factorization for document context-aware recommendation[C]. Proceedings of the 10th ACM Conference on Recommender Systems, Boston, USA, 2016: 233–240. DONG Xing, YU Lei, WU Zhonghuo, et al. A hybrid collaborative filtering model with deep structure for recommender systems[C]. Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, USA, 2017: 1309–1315. 任星怡, 宋美娜, 宋俊德. 基于位置社交网络的上下文感知的兴趣点推荐[J]. 计算机学报, 2017, 40(4): 824–841 doi: 10.11897/SP.J.1016.2017.00824REN Xingyi, SONG Meina, and SONG Junde. Context-aware point-of-interest recommendation in location-based social networks[J]. Chinese Journal of Computer, 2017, 40(4): 824–841 doi: 10.11897/SP.J.1016.2017.00824 GAO Rong, LI Jing, LI Xuefei, et al. A personalized point-of-interest recommendation model via fusion of geo-social information[J]. Neurocomputing, 2018, 273: 159–170 doi: 10.1016/j.neucom.2017.08.020 LIAN Defu, ZHENG Kai, GE Yong, et al. GeoMF++: Scalable location recommendation via joint geographical modeling and matrix factorization[J]. ACM Transactions on Information Systems, 2018, 36(3): 33 doi: 10.1145/3182166 ZDUNEK R. Initialization of nonnegative matrix factorization with vertices of convex polytope[C]. Proceedings of the 11st International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 2012: 448–455. YANG Cheng, SUN Maosong, ZHAO W X, et al. A neural network approach to jointly modeling social networks and mobile trajectories[J]. ACM Transactions on Information Systems, 2017, 35(4): 36 doi: 10.1145/3041658 DENG Shuiguang, HUANG Longtao, XU Guangdong, et al. On deep learning for trust-aware recommendations in social networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(5): 1164–1177 doi: 10.1109/TNNLS.2016.2514368 GAO Huiji, TANG Jiliang, HU Xia, et al. Content-aware point of interest recommendation on location-based social networks[C]. Proceedings of the 29th AAAI Conference on Artificial Intelligence, Austin, Texas, 2015: 1721–1727. ZHANG Fuzheng, YUAN N J, ZHENG Kai, et al. Exploiting dining preference for restaurant recommendation[C]. Proceedings of the 25th International Conference on World Wide Web, Montréal, Canada, 2016: 725–735. LIU Yong, WEI Wei, SUN Aixin, et al. Exploiting geographical neighborhood characteristics for location recommendation[C]. Proceedings of the 23rd ACM International Conference on Information and Knowledge Management, Shanghai, China, 2014: 739–748. LI Huayu, GE Yong, HONG Richang, et al. Point-of-interest recommendations: Learning potential check-ins from friends[C]. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, USA, 2016: 975–984. ORCHAND M. Least square quantization in PCM[J]. IEEE Transaction on Information Theory, 1982, 28(2): 129–137 doi: 10.1109/TIT.1982.1056489 SHI J and MALIK J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888–905 doi: 10.1109/34.868688 -





 下载:
下载:


 下载:
下载:
