Direction of Arrival Estimation for Multiple Frequency Hopping Signals Based on Sparse Bayesian Learning
-
摘要:
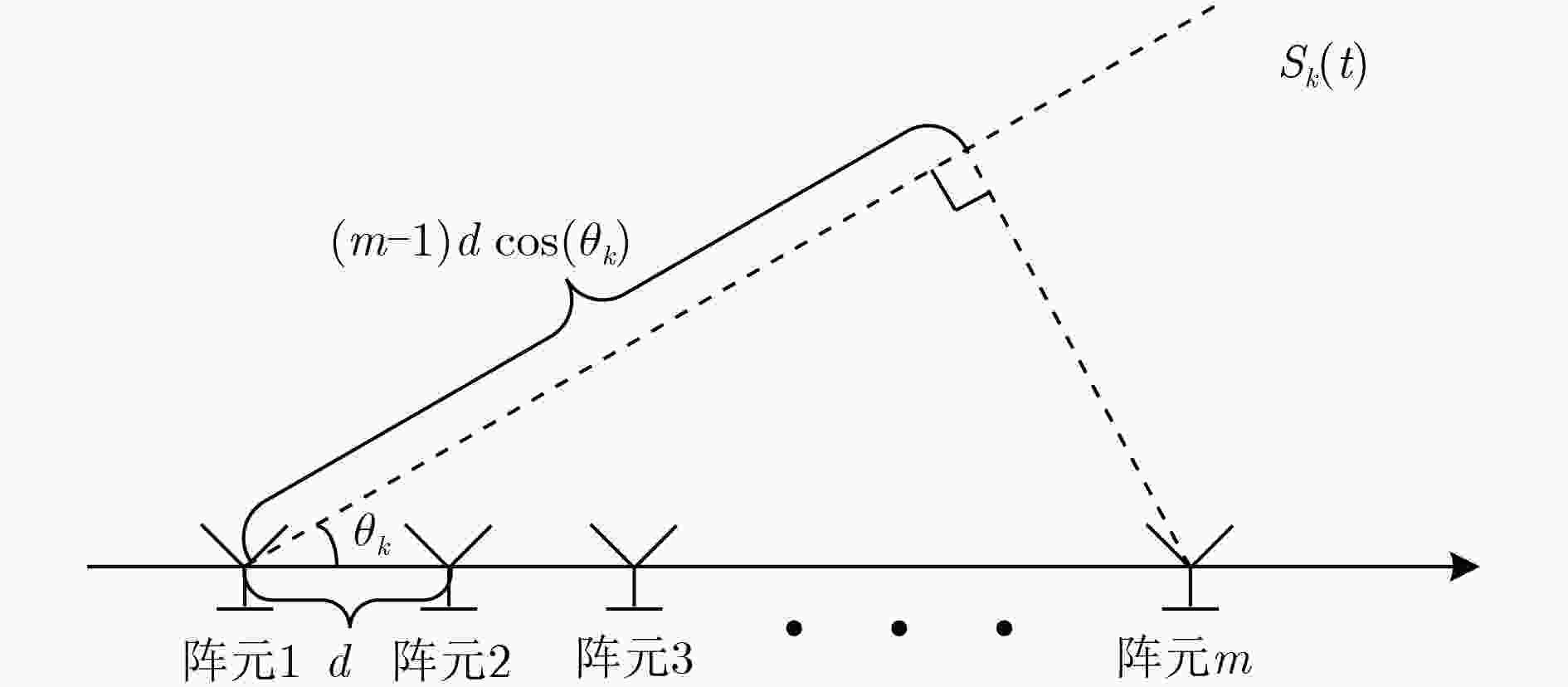
针对多跳频信号空域参数估计问题,该文在稀疏贝叶斯学习(SBL)的基础上,利用跳频信号的空域稀疏性实现了波达方向(DOA)的估计。首先构造空域离散网格,将实际DOA与网格点之间的偏移量建模进离散网格中,建立多跳频信号均匀线阵接收数据模型;然后通过SBL理论得到行稀疏信号矩阵的后验概率分布,用超参数控制偏移量和信号矩阵的行稀疏程度;最后利用期望最大化(EM)算法对超参数进行迭代,得到信号矩阵的最大后验估计以完成DOA的估计。理论分析与仿真实验表明该方法具有良好的估计性能并能适应较少快拍数的情况。
Abstract:To solve the problem of spatial parameter estimation of multi-frequency hopping signals, the sparsity in spatial domain of frequency hopping signals is used to realize the Direction Of Arrival (DOA) estimation based on Sparse Bayesian Learning (SBL). First, the spatial discrete grid is constructed and the offset between the actual DOA and the grid points is modeled into it. The data model of the uniform linear array with multiple frequency hopping signals is established. Then the posterior probability distribution of the sparse signal matrix is obtained by the SBL theory, and the line sparsity of the signal matrix and the offset is controlled by the hyperparameters. Finally, The expectation maximization algorithm is used to iterate the hyper parameters, and the maximum posteriori estimation of the signal matrix is obtained to complete the DOA estimation. Theoretical analysis and simulation experiments show that this method has good estimation performance and can adapt to less snapshots.
-
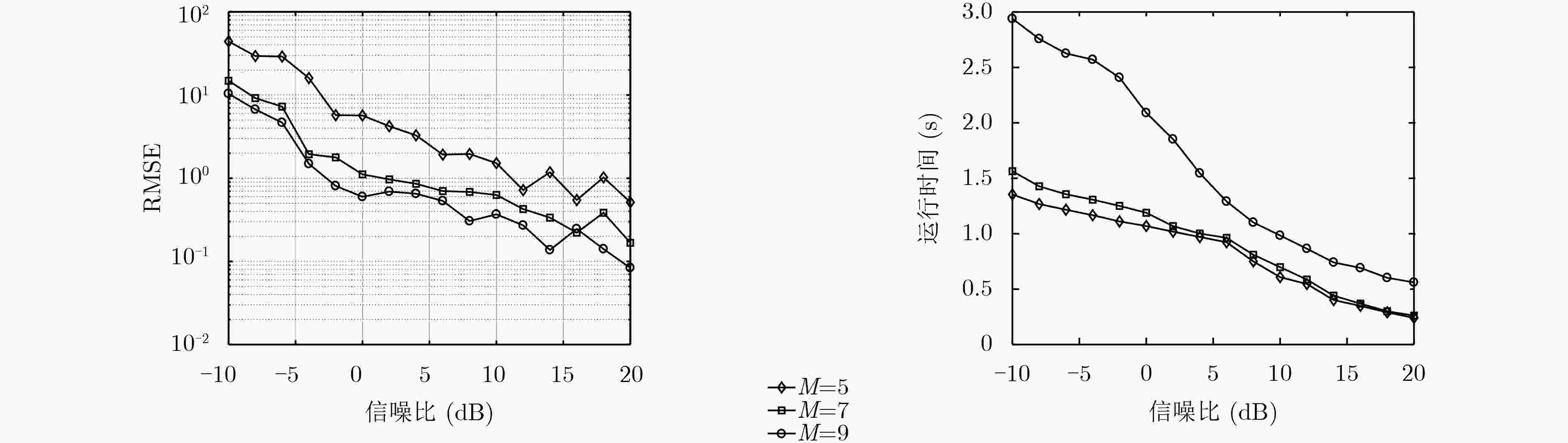
表 1 不同快拍数下算法运行时间的比较(s)
快拍数 20 80 本文算法所用时间 0.3804 0.5915 稀疏重构算法所用时间 0.4066 0.3935 OGSBI算法所用时间 0.6454 0.8428 -
ZHAO Lifan, WANG Lu, BI Guoan, et al. Robust frequency-hopping spectrum estimation based on sparse Bayesian method[J]. IEEE Transactions on Wireless Communications, 2015, 14(2): 781–793. doi: 10.1109/TWC.2014.2360191 HU Chenlin, JIN Y K, NA S Y, et al. Compressive frequency hopping signal detection using spectral kurtosis and residual signals[J]. Wireless Personal Communications An International Journal, 2017, 94(1): 53–67. doi: 10.1007/s11277-015-3156-x 金艳, 李曙光, 姬红兵. 基于柯西分布的跳频信号参数最大似然估计方法[J]. 电子与信息学报, 2016, 38(7): 1696–1702. doi: 10.11999/JEIT151029JIN Yan, LI Shuguang, and JI Hongbing. Maximum-likelihood estimation for frequency-hopping parameters by Cauchy distribution[J]. Journal of Electronics &Information Technology, 2016, 38(7): 1696–1702. doi: 10.11999/JEIT151029 陈利虎, 张尔扬. 基于数字信道化和空时频分析的多网台跳频信号DOA估计[J]. 通信学报, 2009, 30(10): 68–74.CHEN Lihu and ZHANG Eryang. Directions of arrival estimation for multi frequency-hopping signals based on digital channelized receiver and spatial time-frequency analysis[J]. Journal on Communications, 2009, 30(10): 68–74. 陈利虎. 基于空时频分析的多分量跳频信号DOA估计[J]. 系统工程与电子技术, 2011, 33(12): 2587–2592. doi: 10.3969/j.issn.1001-506X.2011.12.04CHEN Lihu. Directions of arrival estimation for multicomponent frequency-hopping signals based on spatial time-frequency analysis[J]. Systems Engineering and Electronics, 2011, 33(12): 2587–2592. doi: 10.3969/j.issn.1001-506X.2011.12.04 ZHANG Chunlei and LI Lichun. Parameter estimation of multi frequency hopping signals based on compressive spatial time-frequency joint analysis[J]. Pacific Journal of Mathematics, 2014, 136(1): 85–101. doi: 10.1109/ICSESS.2014.6933627 STOICA P and NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound[J]. IEEE Transaction on Signal Processing, 1990, 37(5): 720–741. doi: 10.1109/29.17564 张东伟, 郭英, 张坤峰, 等. 多跳频信号频率跟踪与二维波达方向实时估计算法[J]. 电子与信息学报, 2016, 38(9): 2377–2384. doi: 10.11999/JEIT151170ZHANG Dongwei, GUO Ying, ZHANG Kunfeng, et al. Online estimation algorithm of 2D-DOA and frequency tracking for multiple frequency-hopping signals[J]. Journal of Electronics &Information Technology, 2016, 38(9): 2377–2384. doi: 10.11999/JEIT151170 于欣永, 郭英, 张坤峰, 等. 一种高效的多跳频信号2D-DOA估计算法[J]. 系统工程与电子技术, 2018, 40(6): 1363–1370. doi: 10.3969/j.issn.1001-506X.2018.06.25YU Xinyong, GUO Ying, ZHANG Kunfeng, et al. An efficient 2D-DOA estimation algorithm for multi-FH signals[J]. Systems Engineering and Electronics, 2018, 40(6): 1363–1370. doi: 10.3969/j.issn.1001-506X.2018.06.25 LIU Fulai, PENG Lu, WEI Ming, et al. An improved L1-SVD algorithm based on noise subspace for DOA estimation[J]. Progress in Electromagnetics Research, 2012, 29(12): 109–122. doi: 10.2528/PIERC12021203 张坤峰, 郭英, 齐子森, 等. 基于稀疏贝叶斯重构的多跳频信号参数估计[J]. 华中科技大学学报(自然科学版), 2017, 45(1): 97–102. doi: 10.13245/j.hust.170118ZHANG Kunfeng, GUO Ying, QI Zisen, et al. Parameter estimation for multiple frequency-hopping signals based on sparse Bayesian reconstruction[J]. Journal of Huazhong University of Science and Technology, 2017, 45(1): 97–102. doi: 10.13245/j.hust.170118 TIPPING M E. Sparse bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211–244. WIPF D P and RAO B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3704–3716. doi: 10.1109/TSP.2007.894265 LEI Wenying and CHEN Baixiao. High-resolution DOA estimation for closely spaced correlated signals using unitary sparse Bayesian learning[J]. Electronics Letters, 2015, 51(3): 285–287. doi: 10.1049/el.2014.1317 HUANG Qinghua, ZHANG Guangfei, and FANG Yong. Real-valued DOA estimation for spherical arrays using sparse Bayesian learning[J]. Signal Processing, 2016, 125(C): 79–86. doi: 10.1016/j.sigpro.2016.01.009 YANG Jie, YANG Yixin, LIAO Guisheng, et al. A super-resolution direction of arrival estimation algorithm for coprime array via sparse Bayesian learning inference[J]. Circuits Systems & Signal Processing, 2018, 37(5): 1907–1934. doi: 10.1007/s00034-017-0637-z YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378 东润泽, 郭英, 于欣永, 等. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. 空军工程大学学报(自然科学版), 2018, 19(3): 56–61.DONG Runze, GUO Ying, YU Xinyong, et al. A frequency hopping signal detection method based on sparse reconstruction[J]. Journal of Air Force Engineering University(Natural Science Edition) , 2018, 19(3): 56–61. COTTER S F, RAO B D, ENGAN K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2477–2488. doi: 10.1109/TSP.2005.849172 ELDAR Y C and MISHALI M. Robust recovery of signals from a structured union of subspaces[J]. IEEE Transactions on Information Theory, 2009, 55(11): 5302–5316. doi: 10.1109/TIT.2009.2030471 -





 下载:
下载:



 下载:
下载:
