Multi-objective Virtual Network Embedding Algorithm Based on Nash Bargaining
-
摘要:
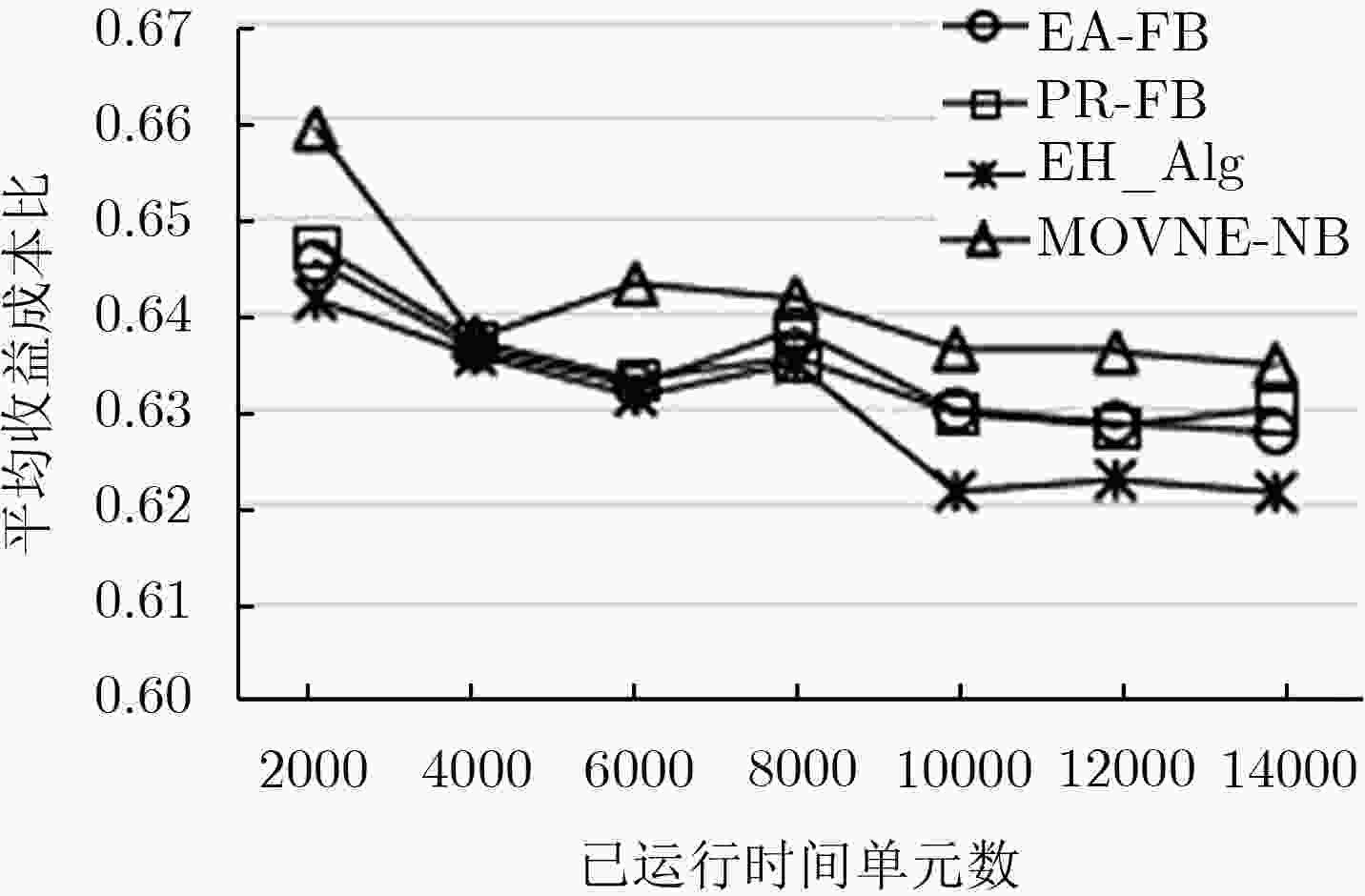
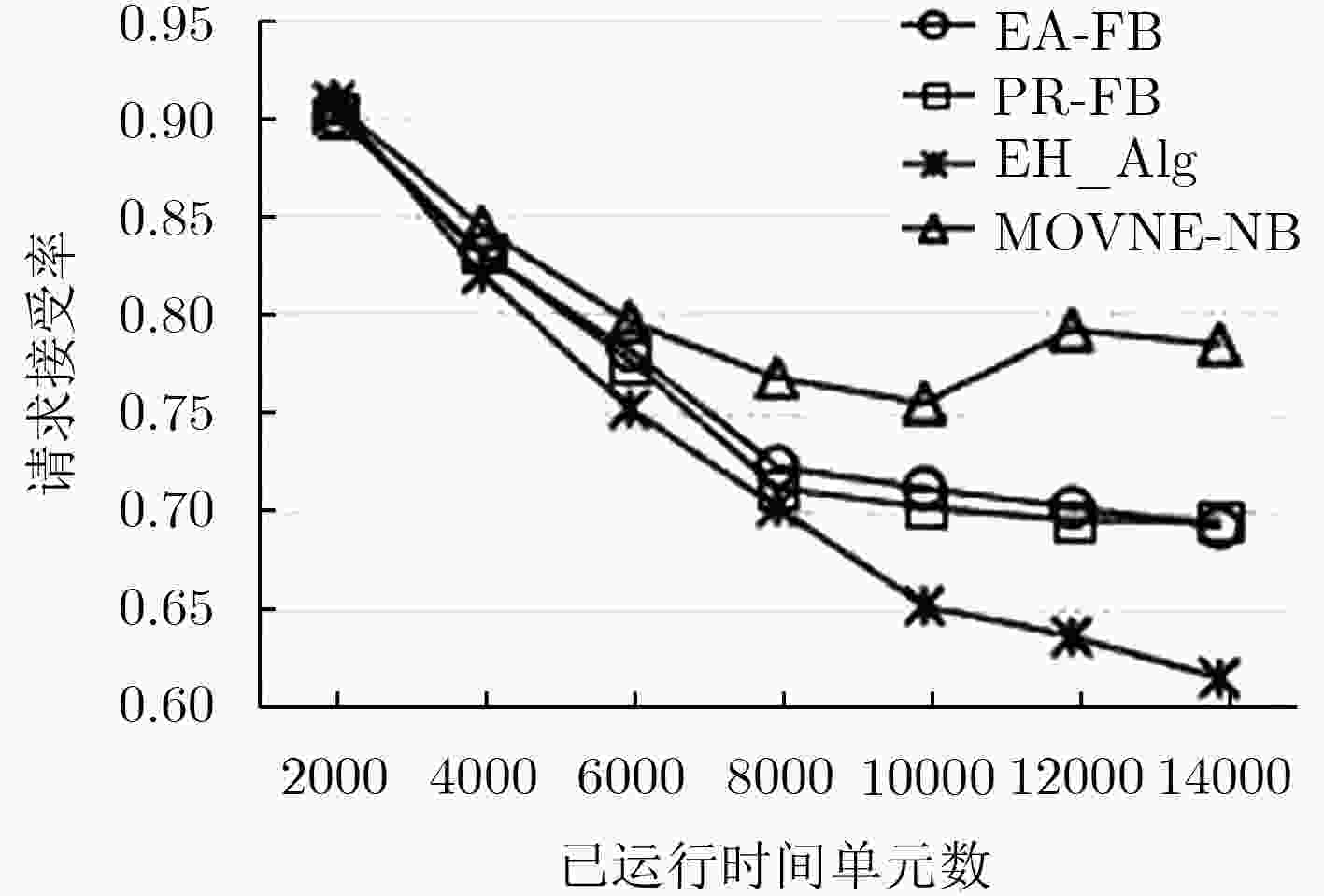
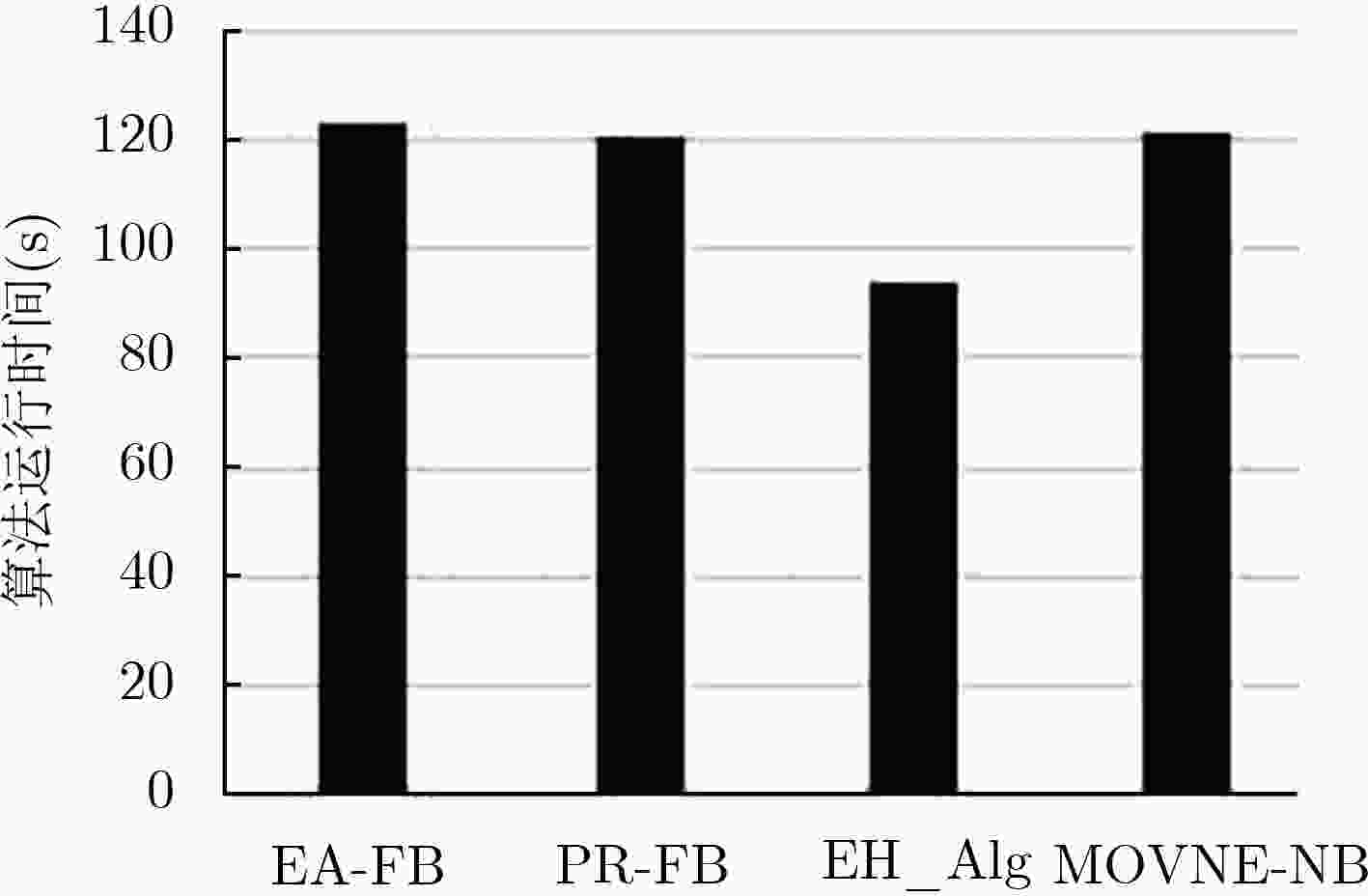
请求接受率和节能是虚拟网映射过程中两个至关重要的指标,然而当前虚拟网映射问题的研究仅考虑单一指标,忽略了两者之间的关联和制约,导致虚拟网映射整体性能下降。该文提出一种基于纳什议价的虚拟网多目标映射算法(MOVNE-NB):利用博弈论谈判技术,在纳什议价的框架下协商虚拟网映射的合理解;提出公平议价机制,避免参与人自私决策而导致议价失败。实验表明,MOVNE-NB算法不仅能产生一个帕累托有效解,且实现了请求接受率和节能的公平折中。
Abstract:Request acceptance rate and energy saving are the two most important indicators in the virtual network mapping process. However, the current virtual network embedding problem considers only a single index, ignoring the correlation and constraints between the two, resulting in a decrease in the overall performance of the virtual network embedding. This paper proposes a Multi-Objective Virtual Network Embedding algorithm based on Nash Bargaining (MOVNE-NB). Firstly negotiating the virtual network embedding problem in the framework of Nash bargaining by using game theory technology. Then a fair bargaining mechanism is put forward to avoid selfish decisions by players and lead to bargaining failures. Experiments show that the MOVNE-NB algorithm can not only produce a Pareto efficient solution, but also achieve a fair tradeoff between request acceptance rate and energy saving.
-
LIANG Chengchao and YU F R. Wireless network virtualization: A survey, some research issues and challenges[J]. IEEE Communications Surveys & Tutorials, 2015, 17(1): 358–380. CHOWDHURY N M M K and BOUTABA R. Network virtualization: State of the art and research challenges[J]. IEEE Communications Magazine, 2009, 47(7): 20–26 doi: 10.1109/MCOM.2009.5183468 CHOWDHURY N M M K and BOUTABA R. A survey of network virtualization[J]. Computer Networks, 2010, 54(5): 862–876 doi: 10.1016/j.comnet.2009.10.017 贾伟, 夏靖波. 跨域虚拟网络映射问题研究[J]. 电子与信息学报, 2016, 38(3): 728–734 doi: 10.11999/JEIT150656JIA Wei and XIA Jingbo. Research on virtual network embedding across multiple domains[J]. Journal of Electronics &Information Technology, 2016, 38(3): 728–734 doi: 10.11999/JEIT150656 CHEN Xiaohua, LI Chenzhi, and JIANG Yunliang. A feedback control approach for energy efficient virtual network embedding[J]. Computer Communications, 2016, 80: 16–32 doi: 10.1016/j.comcom.2015.10.010 JIA Shuxian, JIANG Guiyuan, HE Peilan, et al. Efficient algorithm for energy-aware virtual network embedding[J]. Tsinghua Science & Technology, 2016, 21(4): 407–414 doi: 10.1109/TST.2016.7536718 HE Huajun, ZHAO Yang, WU Jinfu, et al. Cost-aware capacity provisioning for Internet video streaming CDNs[J]. The Computer Journal, 2015, 58(12): 3255–3270 doi: 10.1093/comjnl/bxv015 NONDE L, El-GORASHI T E H, and ELMIRGHANI J M H. Energy efficient virtual network embedding for cloud networks[J]. Journal of Lightwave Technology, 2015, 33(9): 1828–1849 doi: 10.1109/JLT.2014.2380777 LIN Rongping, LUO Shan, WANG Haoran, et al. Energy-aware virtual network embedding in flexi-grid networks[J]. Optics Express, 2017, 25(24): 29699–29713 doi: 10.1364/OE.25.029699 SHI Qiong, ZHAN Liqiang, ZHANG Yaoyuan, et al. Energy-efficiency versus delay tradeoff in wireless networks virtualization[J]. IEEE Transactions on Vehicular Technology, 2018, 67(1): 837–841 doi: 10.1109/TVT.2017.2738024 INES H, WAJDI L, and DJAMAL Z. Exact Multi-objective virtual network embedding in cloud environments[J]. The Computer Journal, 2015, 58(3): 403–415 doi: 10.1093/comjnl/bxu154 ZHANG Peiying, YAO Haipeng, FANG Chao, et al. Multi-objective enhanced particle swarm optimization in virtual network embedding[J]. Eurasip Journal on Wireless Communications & Networking, 2016, 2016(1): 167–175 doi: 10.1186/s13638-016-0669-2 FUDENBERG D and TIROLE J. Game Theory[M]. Cambridge: MIT Press, 1991: 18–26. MUTHOO A. Bargaining Theory with Applications[M]. Cambridge: Cambridge University Press, 1999: 99–118. FISHER R, URY W, and PATTON B. Getting to Yes: Negotiating Agreement without Giving in[M]. USA, Random House Business Books, 1981: 49–50. CHOWDHURY N M M K, RAHMAN M R, and BOUTABA R. Virtual network embedding with coordinated node and link mapping[C]. 2009 IEEE INFOCOM 28th International Conference on Computer Communications, Rio de Janeiro, Brazil, 2009: 783–791. doi: 10.1109/INFCOM.2009.5061987. ZEGURA E W, CALVERT K L, and BHATTACHARJEE S. How to model an Internetwork[C]. Proceedings of IEEE INFOCOM′ 96, Conference on Computer Communications, San Francisco, USA, 1996, 2: 594–602. doi: 10.1109/INFCOM.1996.493353. SIVARAMAN V, VISHWANATH A, ZHAO Zhi, et al. Profiling per-packet and per-byte energy consumption in the NetFPGA Gigabit router[C]. IEEE Conference on Computer Communications Workshops, Shanghai, China, 2011: 331–336. doi: 10.1109/INFCOMW.2011.5928833. ZHANG Xiaoning, WANG Sheng, ZHAO Yangming, et al. Multiobjective optimization for green network routing in game theoretical perspective[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(12): 2801–2814 doi: 10.1109/JSAC.2015.2481202 HAIMES Y Y, LASDON L S, WISMER D A, et al. On a bicriterion formulation of the problems of integrated system identification and system optimization[J]. IEEE Transactions on Systems, Man & Cybernetics, 1971, SMC-1(3): 296–297 doi: 10.1109/TSMC.1971.4308298 -





 下载:
下载:



 下载:
下载:
