Virus Propagation Model and Stability Under the Hybrid Mechanism of “Two-go and One-live”
-
摘要:
随着网络信息系统的发展,网络病毒扩散方式及免疫策略成为网络安全领域研究的热点之一。该文研究了一类新型混合攻击病毒,并根据其特点将这类病毒定义为“去二存一”型病毒。通过分析新型病毒的攻击方式,构建了“去二存一”混合机制下病毒的SEIQRS信息扩散模型。在此基础上,求解对应系统的平衡点,并运用Routh-Hurwitz判据分析了系统基本再生数R0及其对系统稳定性的影响。最后,仿真验证了模型的有效性和稳定性。
Abstract:With the development of network information system, virus propagation and immunization strategy become one of the hot topics in the field of network security. In this paper, a new virus with hybrid attacking is introduced, which can attack network in two modes. One is to attack and infect the network nodes directly, and the another is to hide itself in the nodes by hiding its viral characteristic. According to its characteristics, this type of virus is defined as " Two-go and One-live” and the corresponding virus propagation model is established. Moreover, the stability of the system is studied by solving the equilibrium points and analyzing the basic reproduction number R0. Numerical simulations are presented to verify effectiveness and stability of the novel model.
-
Key words:
- Virus propagation /
- Hybrid mechanism /
- Stability analyzing
-
张书奎, 崔志明, 龚声蓉, 等. 传感器网络病毒感染传播局域控制研究[J]. 电子学报, 2009, 37(4): 877–883. doi: 10.3321/j.issn:0372-2112.2009.04.038ZHANG Shukui, CUI Zhiming, GONG Shengrong, et al. An investigation on local area control of compromised nodes spreading in wireless sensor networks[J]. Acta Electronica Sinica, 2009, 37(4): 877–883. doi: 10.3321/j.issn:0372-2112.2009.04.038 王田, 吴群, 文晟, 等. 无线传感网中移动式蠕虫的抑制与清理[J]. 电子与信息学报, 2016, 38(9): 2202–2207. doi: 10.11999/JEIT151311WANG Tian, WU Qun, WEN Sheng, et al. The inhibition and clearup of the mobile worm in wireless sensor networks[J]. Journal of Electronics &Information Technology, 2016, 38(9): 2202–2207. doi: 10.11999/JEIT151311 E安全. 黑客战术三十六计之" 声东击西”[OL]. https://www.easyaq.com/news/1538639872.shtml, 2017, 11. ZHANG Zizhen and BI Dianjie. Bifurcation analysis in a delayed computer virus model with the effect of external computers[J]. Advances in Difference Equations, 2015, 2015(1): 317–330. doi: 10.1186/s13662-015-0652-y VALDEZ J, GUEVARA P, and AUDELO J. Numerical approaching of SIR epidemic model for propagation of computer worms[J]. IEEE Latin America Transactions, 2015, 13(10): 3452–3460. doi: 10.1109/TLA.2015.7387254 QU Bo and WANG Huijuan. SIS epidemic spreading with correlated heterogeneous infection rates[J]. Physica A: Statistical Mechanics and its Applications, 2017, 472(1): 13–24. TANG Qian and TENG Zhidong. A new Lyapunov function for SIRS epidemic models[J]. Bulletin of the Malaysian Mathematical Sciences Society, 2017, 40(1): 237–258. doi: 10.1007/s40840-016-0315-5 顾海俊, 蒋国平, 夏玲玲. 基于状态概率转移的SIRS病毒传播模型及其临界值分析[J]. 计算机科学, 2016, 43(6): 64–67. doi: 10.11896/j.issn.1002-137X.2016.6A.014GU Haijun, JIANG Guoping, and XIA Lingling. SIRS epidemic model and its threshold based on state transition probability[J]. Computer Science, 2016, 43(6): 64–67. doi: 10.11896/j.issn.1002-137X.2016.6A.014 YANG Luxing and YANG Xiaofan. The impact of nonlinear infection rate on the spread of computer virus[J]. Nonlinear Dynamics, 2015, 82(2): 85–95. 关治洪, 亓玉娟, 姜晓伟, 等. 基于复杂网络的病毒传播模型及其稳定性[J]. 华中科技大学学报, 2011, 39(1): 114–117.GUAN Zhihong, QI Yujuan, JIANG Xiaowei, et al. Virus propagation dynamic model and stability on complex network[J]. Journal Huazhong University of science &Technology, 2011, 39(1): 114–117. XU Degang, XU Xiyang, XIE Yongfang, et al. Optimal control of an SIVRS epidemic spreading model with virus variation based on complex networks[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 48(1): 200–210. KHANH G H and HUY N B. Stability analysis of a computer virus propagation model with antidote in vulnerable system[J]. Acta Mathematica Scientia, 2016, 36(1): 49–61. doi: 10.1016/S0252-9602(15)30077-1 WANG Xu, NI Wei, ZHENG Kangfeng, et al. Virus propagation modeling and convergence analysis in large scale networks[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(10): 2241–2254. doi: 10.1109/TIFS.2016.2581305 TIAN Daxin, LIU Chao, SHENG Zhengguo, et al. Analytical model of spread of epidemics in open finite regions[J]. IEEE Access, 2017, 5(2): 9673–9681. LIU Siyu, JIN Jiyu, and WANG Zhisen. Influence of node mobility on virus spreading behaviors in multi-hop network[J]. EURASIP Journal on Wireless Communications and Networking, 2016, 2016(1): 172–182. doi: 10.1186/s13638-016-0667-4 ZHANG Chunming and HUANG Haitao. Optimal control strategy for a novel computer virus propagation model on scale-free networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 451(1): 251–265. HAN Dun, SUN Mei, and LI Dandan. The virus variation model by considering the degree-dependent spreading rate[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 433(1): 42–50. XU Qichao, SU Zhou, and YANG Kan. Optimal control theory based epidemic information spreading scheme for mobile social users with energy constraint[J]. IEEE Access, 2017, 5(1): 3536–3547. 王小娟, 宋梅, 郭世泽, 等. 基于有向渗流理论的关联微博转发网络信息传播研究[J]. 物理学报, 2015, 64(4): 4502–4510. doi: 10.7498/aps.64.044502WANG Xiaojuan, SONG Mei, GUO Shize, et al. Information spreading in correlated microblog reposting network based on directed percolation theory[J]. Acta Physica Sinica, 2015, 64(4): 4502–4510. doi: 10.7498/aps.64.044502 LI Ming and WANG Binghong. Percolation on networks with dependence links[J]. Chinese Physics B, 2014, 23(7): 6402–6411. -





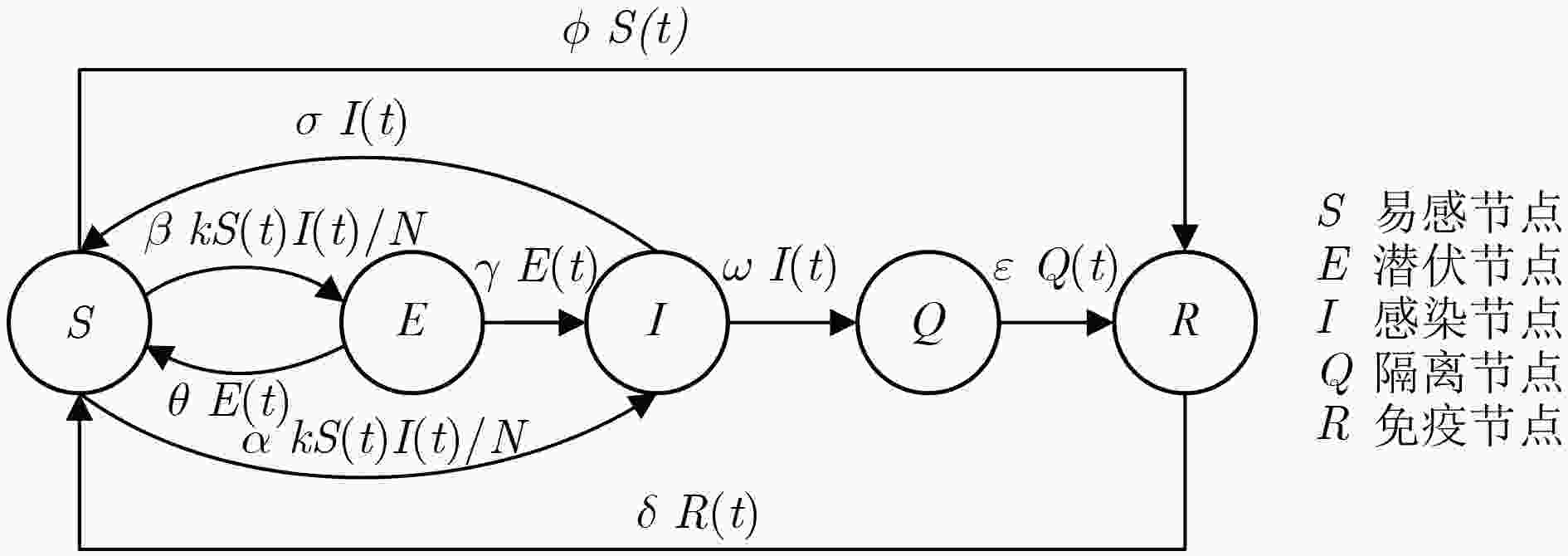
 下载:
下载:
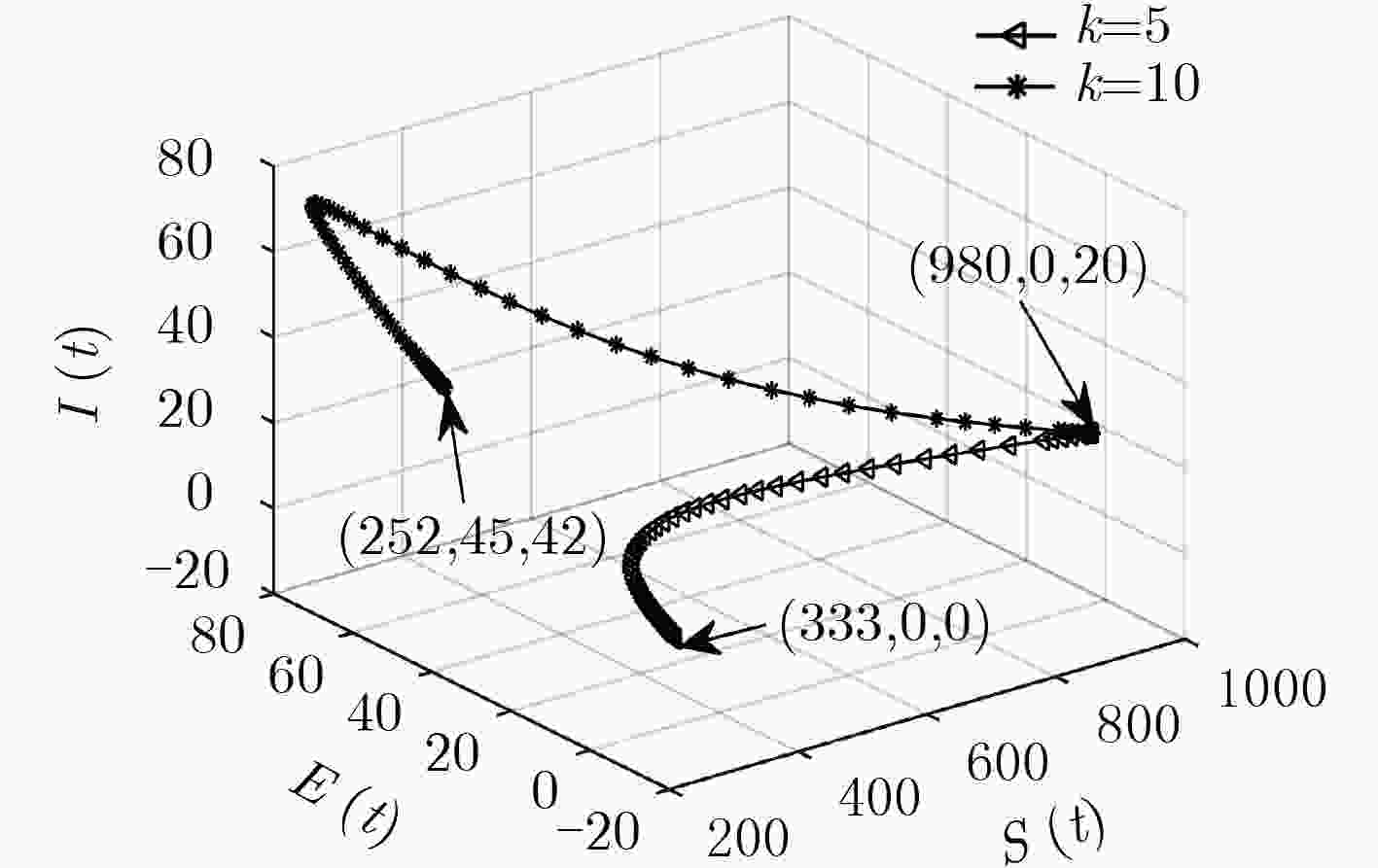
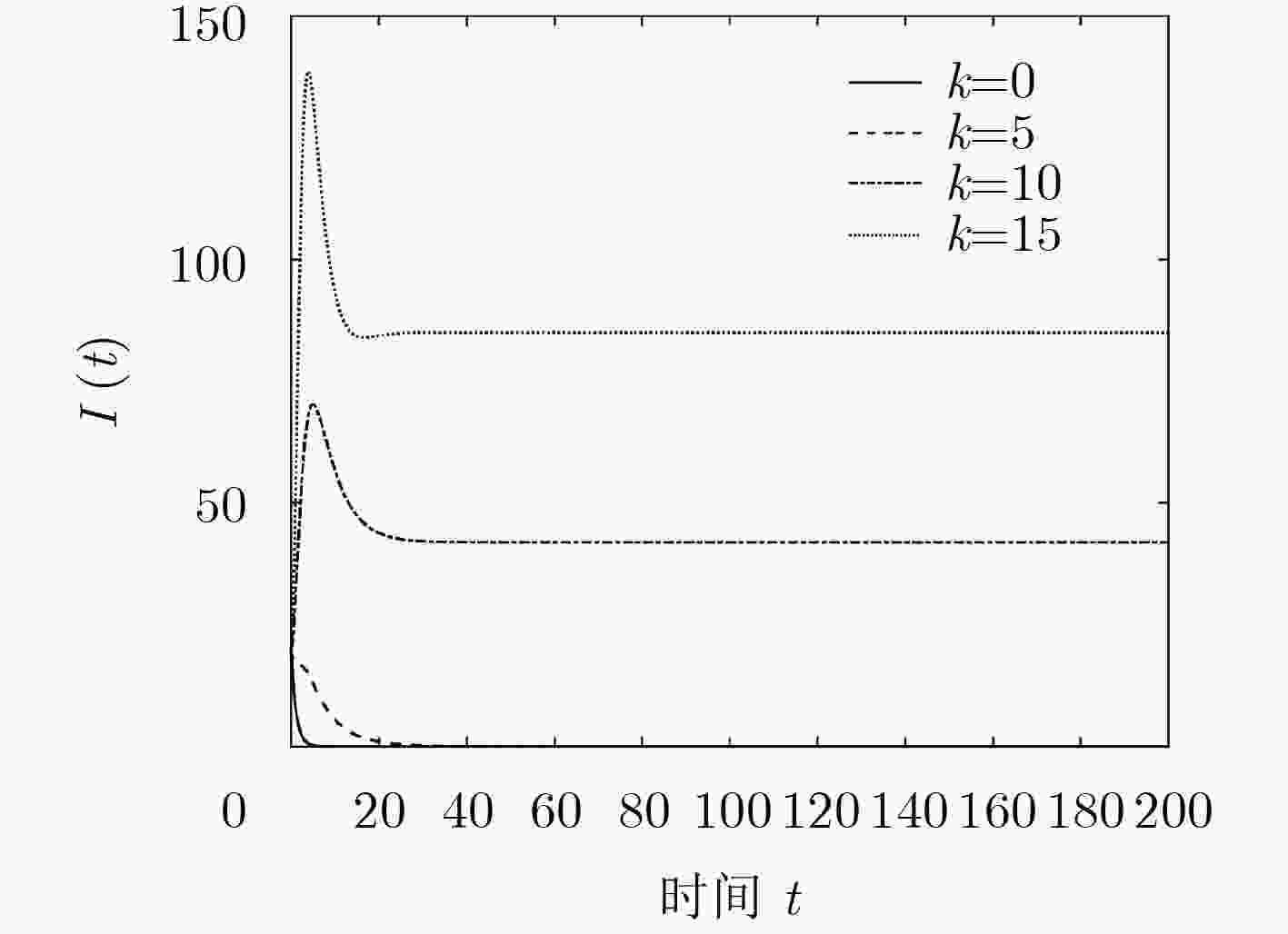
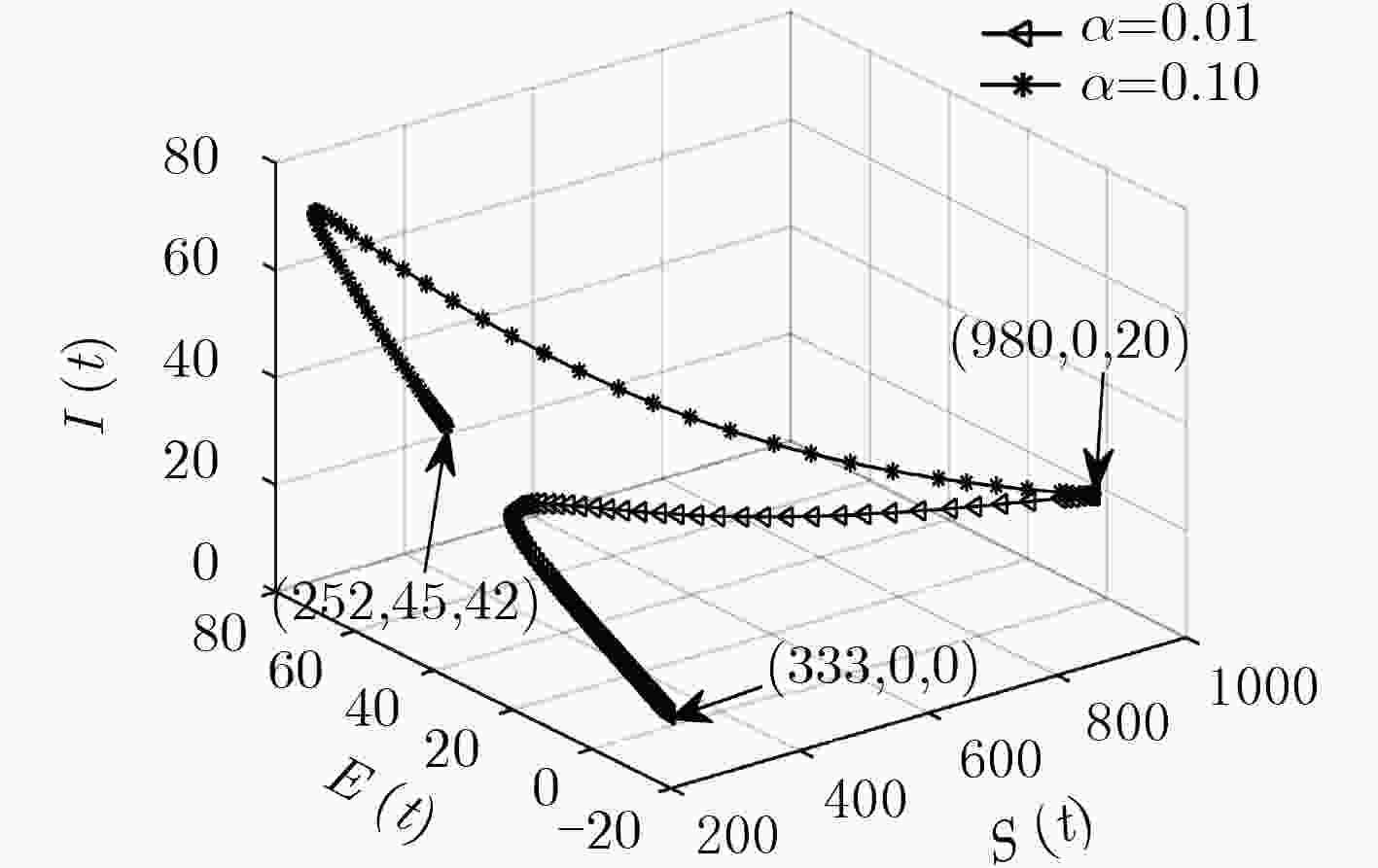


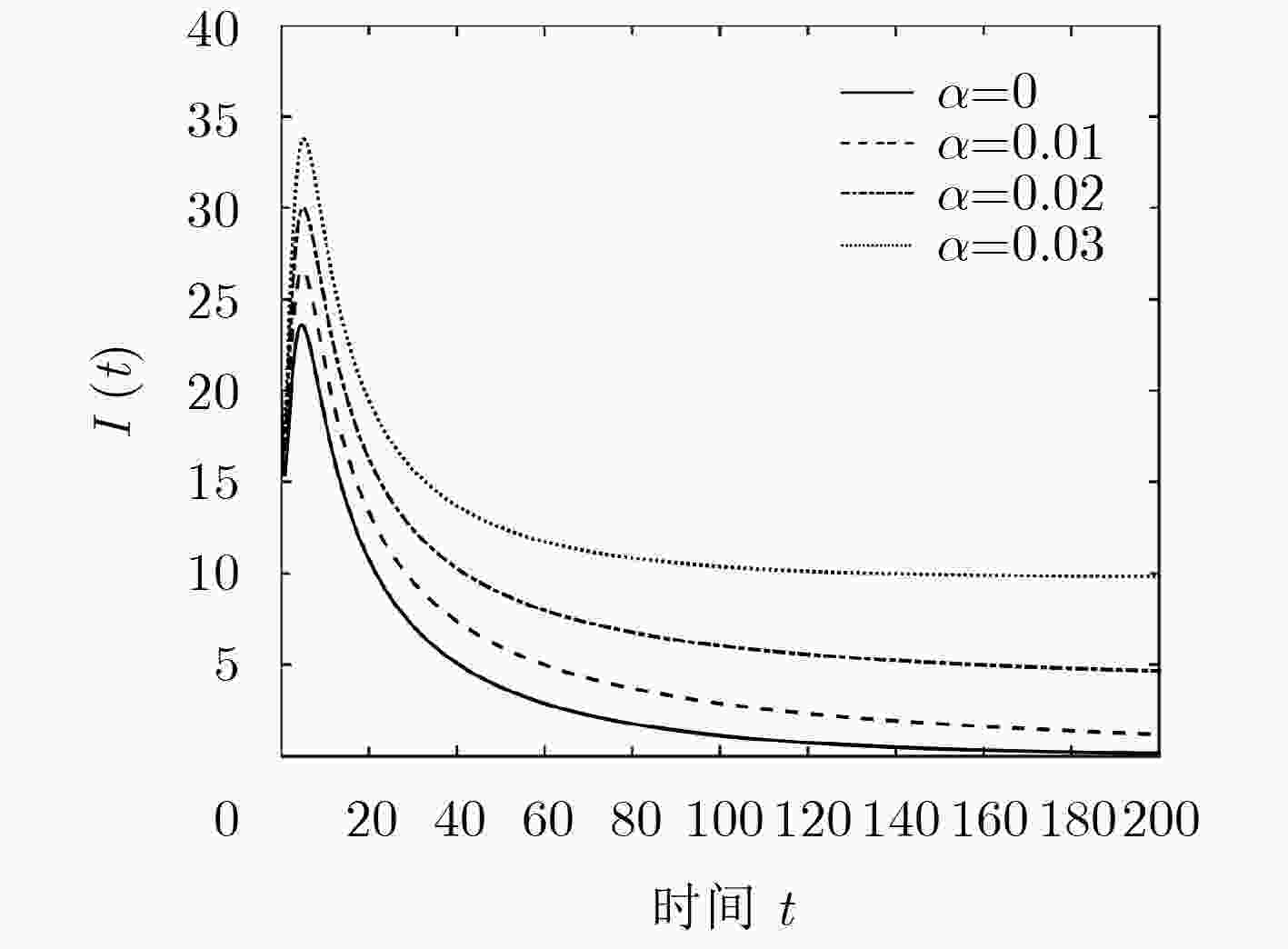

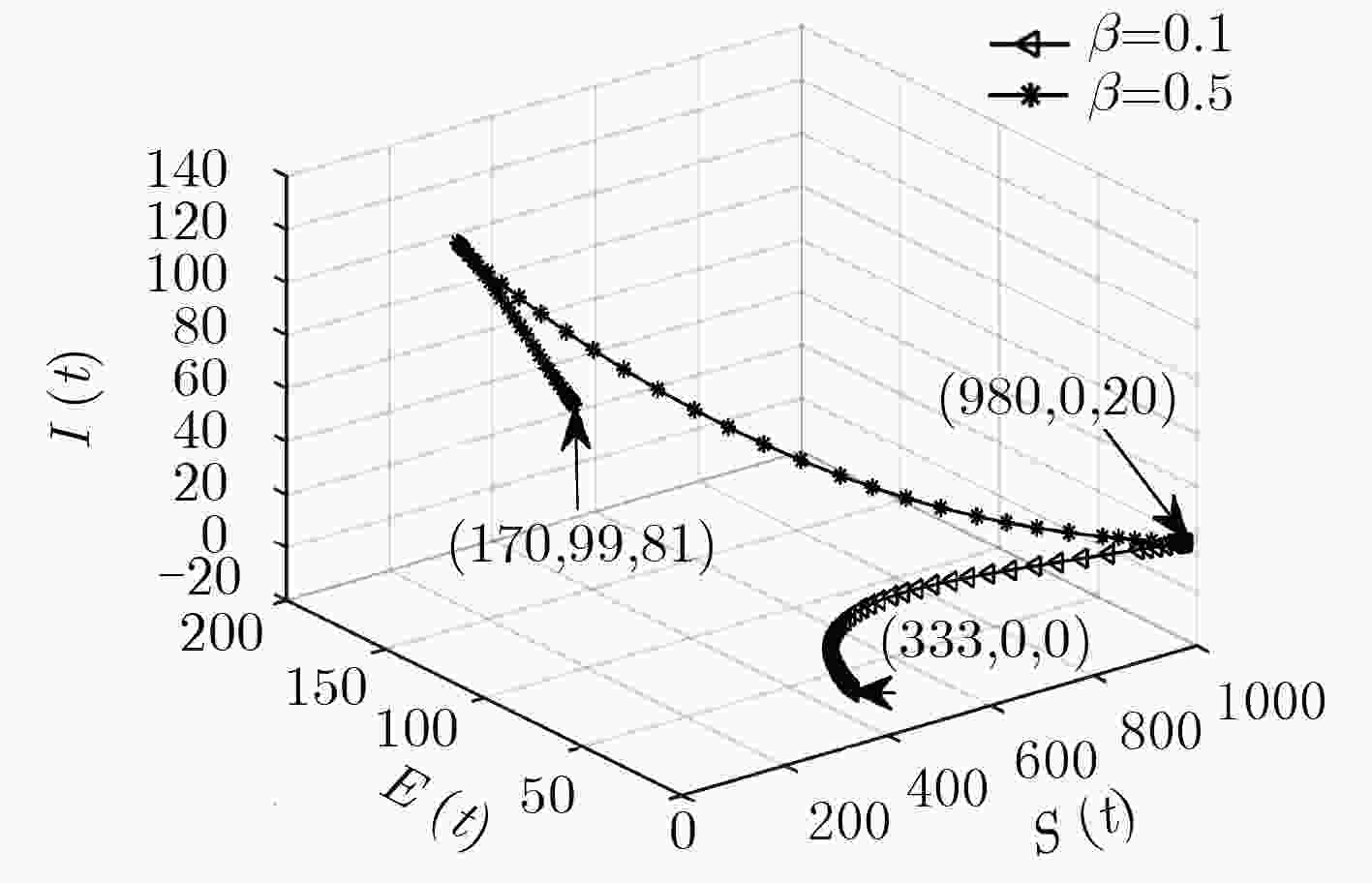


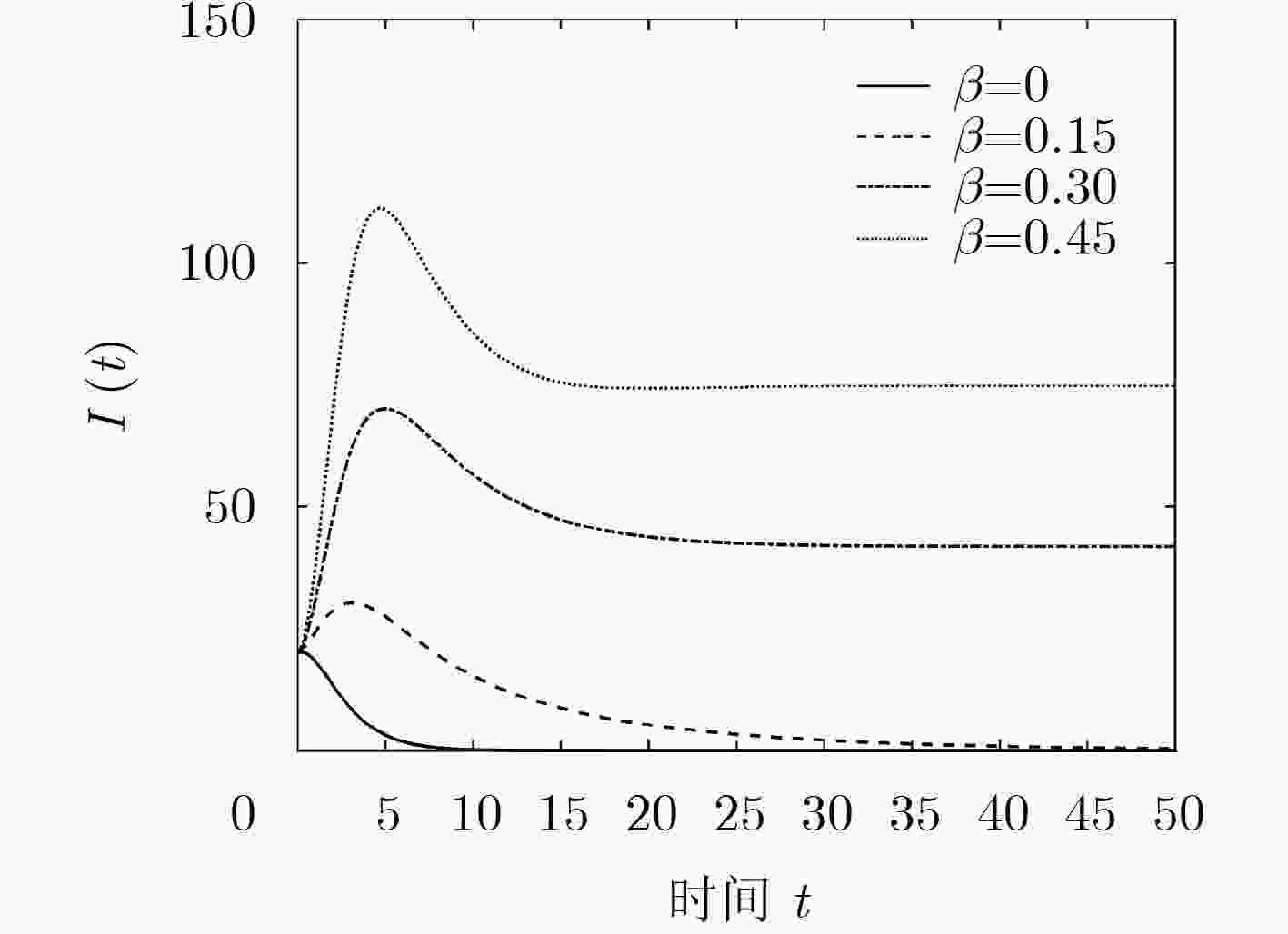

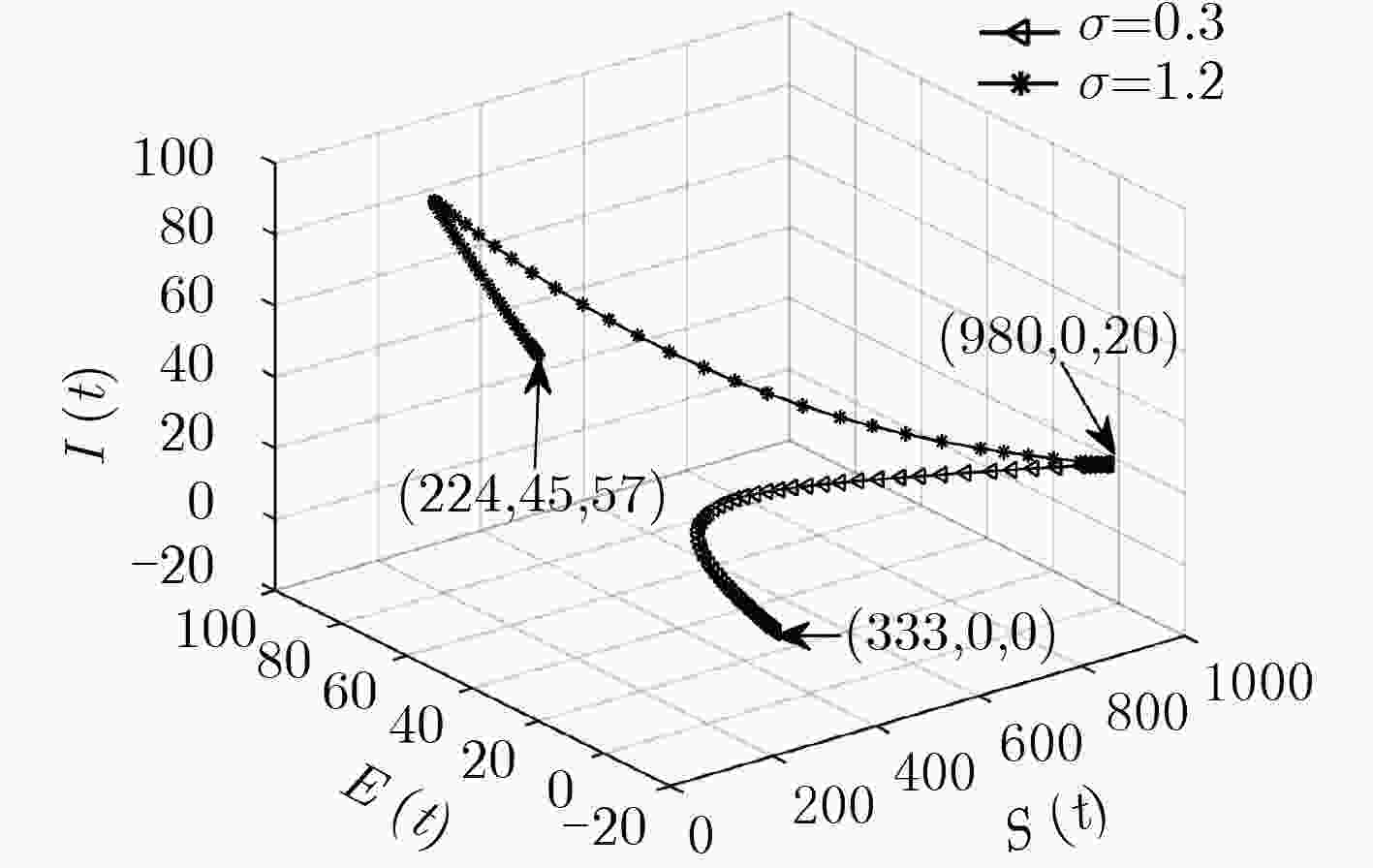





 下载:
下载:
