Real-time Correction Model for Zenith Tropospheric Delay Applied to the Chinese Region
-
摘要:
针对目前对流层延迟修正受限于探空数据不足导致修正效率低的问题,该文结合Saastamoinen和GPT2w模型构建形成组合模型Sa+GPT2w模型,通过利用GPT2w模型提供的高精度气象数据,实现中国地区对流层天顶延迟(ZTD)的实时修正,克服对探空数据的依赖,并用实测数据对计算结果进行验证。以IGS提供的中国地区2015至2017年ZTD时间序列为评估标准时,Sa+GPT2w模型(bias: 1.661 cm, RMS: 4.711 cm)的精度较同等条件下的Sa+EGNOS, Sa+UNB3m和Hop+GPT2w模型分别提升50.5%, 41.9%和37.1%;以GGOS Atmosphere 2017年ZTD数据为标准时,Sa+GPT2w模型(bias: 1.551 cm, RMS: 4.859 cm)的精度相对同等条件下的另3种模型分别提升49.5%, 38.5%和46.8%;最后对Sa+EGNOS, Sa+UNB3m和Sa+GPT2w模型在ZTD修正中误差结果的时空分布特征进行分析。研究结果可为在中国地区的导航定位、大气折射研究中,应用不同气象参数模型进行ZTD修正的有效性和可能达到的精度提供参考。
-
关键词:
- 对流层天顶延迟 /
- Saastamoinen模型 /
- GPT2w模型 /
- EGNOS模型 /
- UNB3m模型
Abstract:In view of the correction for tropospheric delay is limited by the shortage of sounding data, which leads to the problem that the low correction efficiency, this paper proposes a model named Sa+GPT2w, combining Saastamoinen model with GPT2w model. In this paper, the real-time correction for Zenith Tropospheric Delay (ZTD) over China is realized by using the high-precision meteorological values provided by the GPT2w model, and the results are verified by the measured data. Taking the ZTD in 2015-2017 of International GNSS Service(IGS) as a reference, the accuracy of the Sa+GPT2w model (bias: 1.661 cm, RMS: 4.711 cm) rises by 50.5%, 41.9% and 37.1%, respectively, relative to the Sa+EGNOS, Sa+UNB3m and the Hop+GPT2w models. Moreover, using the ZTD from Global Geodetic Observing System (GGOS) in 2017 as a standard, the Sa+GPT2w model (bias: 1.551 cm, RMS: 4.859 cm) improves the accuracy by 49.5%, 38.5% and 46.8% relative to other three models, respectively. Finally, this paper analyzes the temporal and spatial distribution characteristics of the bias and RMS of the above three models. The results provide a significant reference for the effectiveness of correction for ZTD by using different meteorological models in the research of navigation and atmospheric refraction over China.
-
Key words:
- Zenith Tropospheric Delay (ZTD) /
- Saastamoinen model /
- GPT2w model /
- EGNOS model /
- UNB3m model
-
表 1 中国地区IGS测站信息(按纬度升序排列)
ID 测站 纬度(°N) 经度(°E) 高程(m) A TCMS 24.80 120.99 77.3 B TWTF 24.95 121.16 184.0 C KUNM 25.03 102.80 2019.1 D LHAZ 29.66 91.10 3622.0 E WUHN 30.53 114.36 42.6 F SHAO 31.10 121.20 22.1 G XIAN 34.37 109.22 498.5 H BJFS 39.61 115.89 98.3 I GUAO 43.47 87.17 2049.2 J URUM 43.59 87.63 917.9 K CHAN 43.79 125.44 253.7 表 2 相对IGS测站数据的误差统计结果(cm)
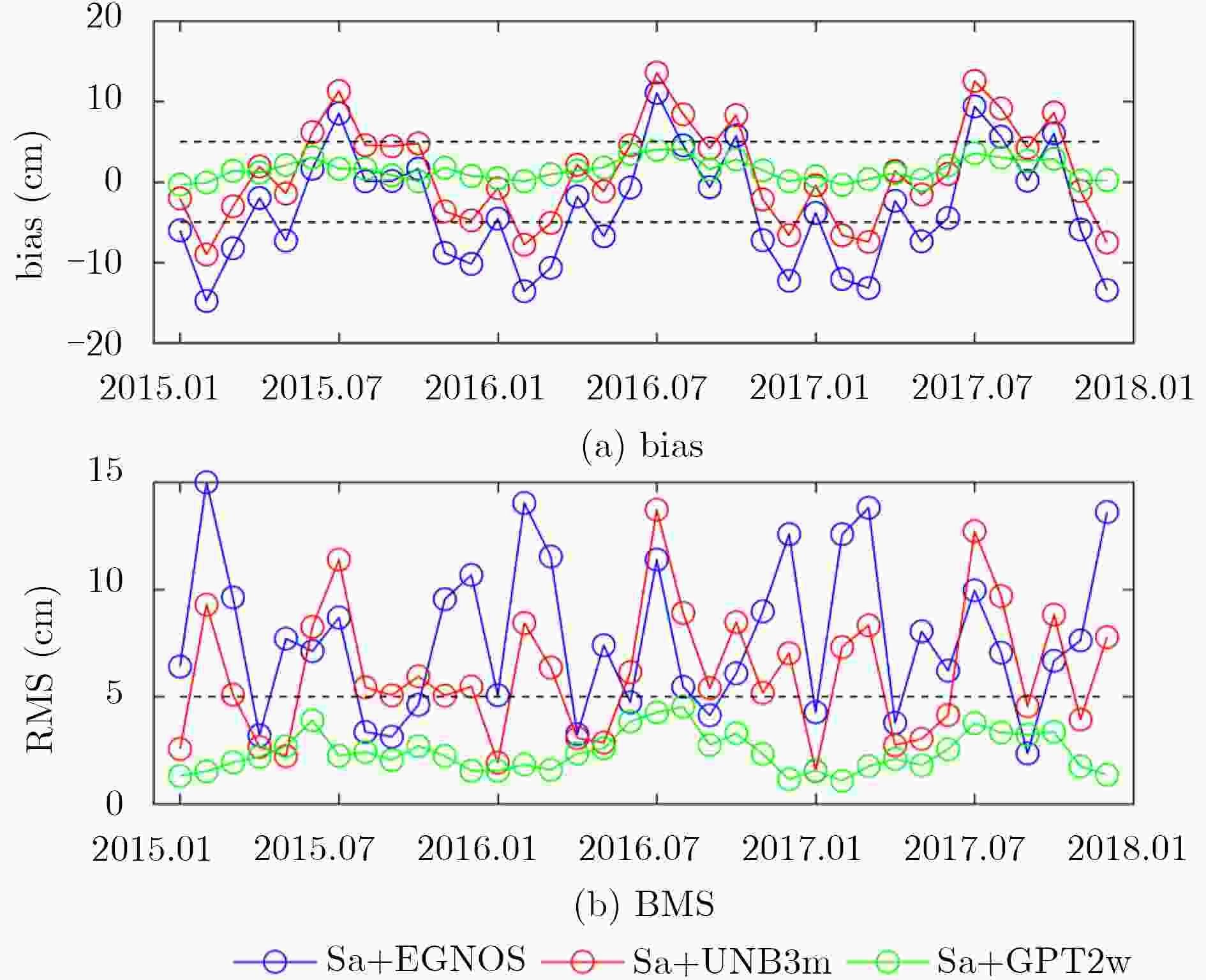
ID 年 Sa+EGNOS Sa+UNB3m Sa+GPT2w Hop+GPT2w bias RMS bias RMS bias RMS bias RMS A 2015 1.048 7.969 2.509 8.328 1.615 5.883 0.911 5.641 2016 2.159 8.585 3.621 9.126 2.729 5.969 2.025 5.700 2017 1.312 8.385 2.773 8.777 1.879 5.811 1.175 5.644 B 2015 0.214 7.736 2.622 8.148 1.497 5.768 1.951 5.906 2016 1.100 8.216 3.508 8.854 2.386 5.743 2.839 5.956 2017 0.316 8.102 2.724 8.519 1.600 5.649 2.053 5.804 C 2015 –6.939 9.817 3.631 7.251 0.530 3.595 10.546 11.207 2016 –6.728 9.753 3.839 7.502 0.742 3.813 10.771 11.466 2017 –6.756 9.977 3.814 7.634 0.713 3.732 10.735 11.417 D 2015 –10.197 11.839 1.494 4.427 0.355 1.667 12.816 12.938 2016 –9.778 11.908 1.899 5.330 0.765 2.039 13.221 13.347 2017 –10.007 12.117 1.626 5.224 0.486 1.906 12.95 13.055 E 2015 –2.216 10.376 –0.799 10.115 3.739 7.087 3.057 6.748 2016 –1.250 11.535 0.160 11.381 4.710 8.061 4.028 7.673 2017 –1.468 11.776 –0.060 11.577 4.485 7.843 3.803 7.465 F 2015 –2.810 11.278 –1.492 11.002 2.263 7.479 1.285 7.237 2016 –1.591 11.837 –0.271 11.675 3.479 7.839 2.502 7.432 2017 –2.531 12.166 –1.201 11.896 2.545 6.999 1.567 6.692 G 2015 –4.477 9.843 –0.053 8.354 1.763 5.257 3.966 6.345 2016 –3.738 10.055 0.678 8.896 2.493 5.313 4.696 6.648 2017 –4.066 10.106 0.358 8.816 2.172 5.314 4.375 6.526 H 2015 –3.988 9.464 –1.637 8.703 1.136 4.207 0.875 4.152 2016 –3.576 10.227 –1.228 9.639 1.546 4.929 1.286 4.822 2017 –4.088 10.626 –1.736 9.861 1.038 4.811 0.777 4.743 I 2015 –4.156 7.327 2.122 4.873 0.656 2.259 10.206 10.429 2016 –3.727 7.334 2.541 5.408 1.073 2.727 10.615 10.906 2017 –4.202 7.415 2.100 4.927 0.634 2.184 10.177 10.385 J 2015 –3.051 6.980 1.290 5.517 1.115 3.320 5.437 6.261 2016 –2.440 7.308 1.890 6.324 1.711 4.069 6.033 7.064 2017 –3.071 7.117 1.269 5.619 1.095 3.228 5.417 6.202 K 2015 –3.780 8.453 –1.401 7.474 0.640 3.447 1.282 3.654 2016 –3.531 8.846 –1.155 8.008 0.882 3.712 1.524 3.907 2017 –4.092 9.337 –1.716 8.323 0.327 3.815 0.969 3.922 平均 –3.397 9.509 1.021 8.106 1.661 4.711 5.026 7.494 表 3 相对GGOS格网数据的误差统计结果(cm)
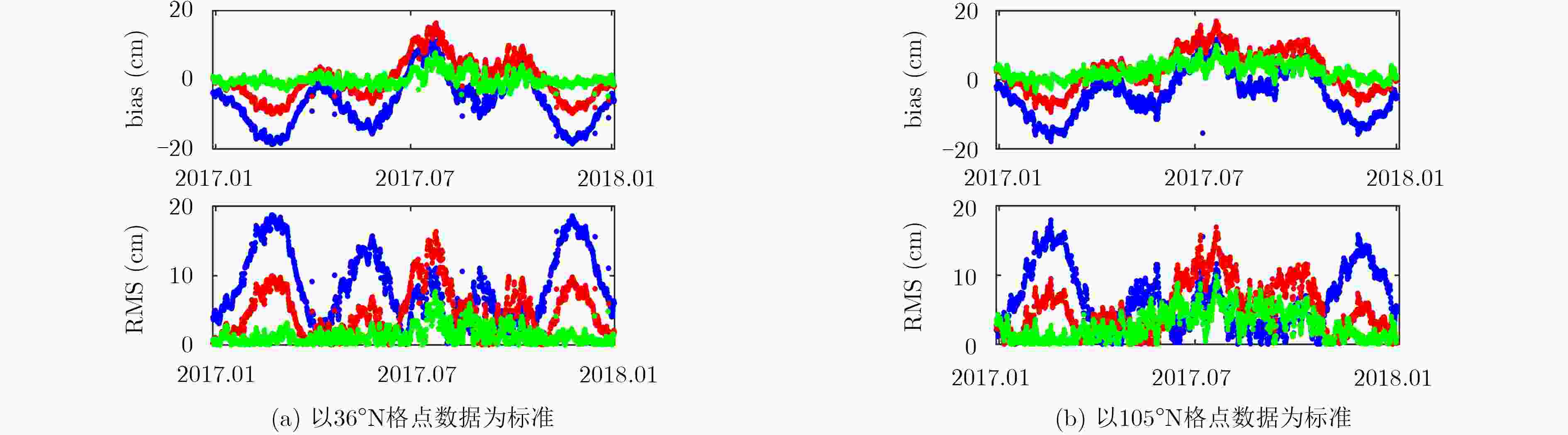
统计类型 Sa+EGNOS Sa+UNB3m Sa+GPT2w Hop+GPT2w bias Min –6.961 –0.812 –0.086 2.716 Max 1.932 3.461 3.445 9.473 Mean –3.605 1.393 1.551 6.581 RMS Min 7.768 5.480 2.585 6.928 Max 11.428 10.010 7.284 11.786 Mean 9.631 7.899 4.859 9.135 表 4 相对IGS数据的误差统计结果(cm)
ID 年份 Sa+EGNOS Sa+UNB3m Sa+GPT2w bias RMS bias RMS bias RMS B 2012 0.240 7.435 2.648 7.900 1.775 5.965 2018 –7.218 9.611 –4.839 7.940 –0.058 5.082 G 2012 –4.849 10.676 –0.419 9.080 1.375 5.153 2018 –11.801 13.128 –7.368 8.823 –0.069 2.302 I 2012 –4.717 7.863 1.564 4.861 0.086 2.005 2018 –8.477 9.787 –1.877 3.303 –0.303 1.104 -
赵静旸, 宋淑丽, 陈钦明, 等. 基于垂直剖面函数式的全球对流层天顶延迟模型的建立[J]. 地球物理学报, 2014, 57(10): 3140–3153. doi: 10.6038/cjg20141005ZHAO Jingyang, SONG Shuli, CHEN Qinming, et al. Establishment of a new global model for zenith tropospheric delay based on functional expression for its vertical profile[J]. Chinese Journal of Geophysics, 2014, 57(10): 3140–3153. doi: 10.6038/cjg20141005 姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218–2227. doi: 10.6038/cjg20130709YAO Yibin, HE Changyong, ZHANG Bao, et al. A new global zenith tropospheric delay model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218–2227. doi: 10.6038/cjg20130709 HOPFIELD H S. Troposphere effect on electromagnetic measured range: Prediction from surface weather data[J]. Radio Science, 1971, 6(3): 357–367. doi: 10.1029/RS006i003p00357 SAASTAMOINEN J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites[J]. Use of Artificial Satellites for Geodesy, 1972, 15(6): 247–251. doi: 10.1029/GM015p0247 杨徉, 喻国荣, 潘树国, 等. 一种综合的对流层延迟模型算法[J]. 东南大学学报(自然科学版), 2013, 43(S2): 418–422. doi: 10.3969/j.issn.1001-0505.2013.S2.043YANG Yang, YU Guorong, PAN Shuguo, et al. A comprehensive algorithm using fusion of tropospheric delay models[J]. Journal of Southeast University(Natural Science Edition) , 2013, 43(S2): 418–422. doi: 10.3969/j.issn.1001-0505.2013.S2.043 姚宜斌, 张豹, 严凤, 等. 两种精化的对流层延迟改正模型[J]. 地球物理学报, 2015, 58(5): 1492–1501. doi: 10.6038/cjg20150503YAO Yibin, ZHANG Bao, YAN Feng, et al. Two new sophisticated models for tropospheric delay corrections[J]. Chinese Journal of Geophysics, 2015, 58(5): 1492–1501. doi: 10.6038/cjg20150503 刘继业, 陈西宏, 刘赞. 对流层散射双向时间比对中对流层斜延迟实时估计[J]. 电子与信息学报, 2018, 40(3): 587–593. doi: 10.11999/JEIT170581LIU Jiye, CHEN Xihong, and LIU Zan. Real-time estimation of tropospheric slant delay in two-way troposphere time transfer[J]. Journal of Electronics &Information Technology, 2018, 40(3): 587–593. doi: 10.11999/JEIT170581 滑中豪, 柳林涛, 梁星辉. GPT2w模型检验以及对流层模型的参数互融[J]. 武汉大学学报:信息科学版, 2017, 42(10): 1468–1473. doi: 10.13203/j.whugis20150758HUA Zhonghao, LIU Lintao, and LIANG Xinghui. An assessment of GPT2w model and fusion of a troposphere model with in situ data[J]. Geomatics and Information Science of Wuhan University, 2017, 42(10): 1468–1473. doi: 10.13203/j.whugis20150758 施宏凯, 何秀凤, 王俊杰. 全球气压气温模型在中国地区的精度分析[J]. 大地测量与地球动力学, 2017, 37(8): 841–844. doi: 10.14075/j.jgg.2017.08.014SHI Hongkai, HE Xiufeng, and WANG Junjie. Accuracy analyses of global pressure and temperature model in China[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 841–844. doi: 10.14075/j.jgg.2017.08.014 LAGLER K, SCHINDELEGGER M, and NILSSON T. GPT2: Empirical slant delay model for radio space geodetic tech-niques[J]. Geophysical Research Letters, 2013, 40(6): 1069–1073. doi: 10.1002/grl.50288 BÖHM J, MÖLLER G, SCHINDELEGGER M, et al. Development of an improved empirical model for slant delays in the troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433–441. doi: 10.1007/s10291-014-0403-7 BRAUN J, ROCKEN C, and WARE R. Validation of line-of-sight water vapor measurements with GPS[J]. Radio Science, 2001, 36(3): 459–472. doi: 10.1029/2000RS002353 姚宜斌, 徐星宇, 胡羽丰. GGOS对流层延迟产品精度分析及在PPP中的应用[J]. 测绘学报, 2017, 46(3): 278–287. doi: 10.11947/j.AGCS.2017.20160383YAO Yibin, XU Xingyu, and HU Yufeng. Precision analysis of GGOS tropospheric delay product and its application in PPP[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 278–287. doi: 10.11947/j.AGCS.2017.20160383 ASKNE J and NORDIUS H. Estimation of tropospheric delay for microwaves from surface weather data[J]. Radio Science, 1987, 22(3): 379–386. doi: 10.1029/RS022i003p00379 NIGEL P and ALAN D. Assessment of EGNOS tropospheric correction model[J]. Journal of Navigation, 1999, 54(1): 37–55. LEANDRO R F, LANGLEY R B, and SANTOS M C. UNB3m_pack: A neutral atmosphere delay package for radiometric space techniques[J]. GPS Solutions, 2008, 12(1): 65–70. doi: 10.1007/s10291-007-0077-5 QU Weijing, ZHU Wenyao, SONG Shuli, et al. Evaluation of the precision of three tropospheric delay correction models[J]. Chinese Astronomy and Astrophysics, 2008, 32(4): 429–438. doi: 10.1016/j.chinastron.2008.10.010 中国天气网. 2016年中国十大天气气候事件评选结果[OL]. http://news.weather.com.cn/2016/12/2638475.shtml. 2016.12. -






 下载:
下载:


 下载:
下载:
