Estimation of Ionospheric Incoherent Scatter Spectrum and Autocorrelation Function
-
摘要:
非相干散射谱对电离层各物理参数的研究具有至关重要的作用。现有非相干散射谱模型推导和计算较为复杂,且无法给出相应的自相关函数模型。该文重新推导了电离层非相干谱的简化模型,并提出相应的自相关函数模型。在此基础上,针对非相干散射信号处理中零时延处距离模糊大、分辨率较低,导致自相关函数在不同时延处均衡性较差,影响电离层散射谱估计性能的问题,提出使用自相关函数模型估计零时延自相关值的数据拟合方法。考虑到计算复杂度,提出利用多项式函数逼近自相关函数模型的快速实现方法。最后,通过对实测回波数据处理结果的对比分析,证明了该方法的可行性,对提高电离层探测精度具有重要意义。
Abstract:Incoherent scatter spectrum plays an important role in studying the physical parameters of the ionosphere. The conventional theoretical model of incoherent scatter spectrum for derivation and calculation is extremely complicated and the model of the autocorrelation function can not be obtained . In this paper, the simplified model of ionospheric incoherent scatter spectrum is re-derived and the corresponding autocorrelation function is proposed. In the procedure of traditional incoherent scattering radar signal processing, the autocorrelation function is imbalance at different delays. This is mainly because the range resolution of zero-lag is very low, which affects the estimated performance of ionospheric scatter spectrum. Focus on this problem, a method based on data fitting is proposed to estimate the autocorrelation at zero-lag. Considering the computational complexity, a fast implementation method by polynomial functions is proposed to approach the autocorrelation function. Finally, experimental results on real echo data demonstrate the correctness and efficiency of the proposed method, which is of great significance for ionospheric detection.
-
GORDON W E. Incoherent scattering of radio waves by free electrons with applications to space exploration by radar[J]. Proceedings of the Ire, 2007, 46(11): 1824–1829. doi: 10.1109/JRPROC.1958.286852 WEN C H, BRICZINSKI S J, LIVNEH D J, et al. Pulse-level interference and meteor processing of Arecibo ISR data[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2007, 69(9): 973–980. doi: 10.1016/j.jastp.2007.03.004 EVANS J V. Theory and practice of ionosphere study by Thomson scatter radar[J]. Proceedings of the IEEE, 1969, 57(4): 496–530. doi: 10.1109/PROC.1969.7005 王凯丽, 姚明, 邓晓华. 非相干散射雷达电离层参数提取简化算法的仿真[J]. 南昌大学学报(工科版), 2017, 39(2): 200–204. doi: 10.13764/j.cnki.ncdg.2017.02.019WANG Kaili, YAO Ming, and DENG Xiaohua. Simulation on a simplified algorithm for ionospheric incoherent scatter radar parameter extraction[J]. Journal of Nanchang University (Engineering &Technology) , 2017, 39(2): 200–204. doi: 10.13764/j.cnki.ncdg.2017.02.019 郑传青, 吴健. 高纬电离层中非麦克斯韦分布等离子体的非相干散射谱的模拟[J]. 地球物理学报, 1994, 37(4): 433–438. doi: 10.3321/j.issn:0001-5733.1994.04.003ZHENG Chuanqing and WU Jian. A computation of the incoherent radar spectra of non-maxwellian plasma in the high-latitude ionosphere[J]. Chinese Journal of Geophysics, 1994, 37(4): 433–438. doi: 10.3321/j.issn:0001-5733.1994.04.003 徐彬, 吴振森, 吴健, 等. 碰撞等离子体的非相干散射谱[J]. 物理学报, 2009, 58(7): 5104–5110. doi: 10.3321/j.issn:1000-3290.2009.07.115XU Bin, WU Zhensen, WU Jian, et al. Incoherent scatter spectrum of a collisional plasma[J]. Acta Physica Sinica, 2009, 58(7): 5104–5110. doi: 10.3321/j.issn:1000-3290.2009.07.115 薛昆, 许正文, 吴健, 等. 高纬极区离子速度分布函数多项式解及非相干散射谱计算[J]. 空间科学学报, 2015, 35(4): 424–437. doi: 10.11728/cjss2015.04.424XUE Kun, XU Zhengwen, WU Jian, et al. Polynomial solutions of the ion velocity distributions and the calculation of incoherent scatter spectra in the high-latitude auroral ionosphere[J]. Chinese Journal of Space Science, 2015, 35(4): 424–437. doi: 10.11728/cjss2015.04.424 金旺, 杨玉峰, 李清亮, 等. 曲靖非相干散射雷达在空间碎片探测中的应用[J]. 电子学报, 2016, 46(1): 252–256. doi: 10.3969/j.issn.0372-2112.2018.01.035JIN Wang, YANG Yufeng, LI Qingliang, et al. Application of Qujing incoherent scattering radar in space debris detection[J]. Acta Electronica Sinica, 2016, 46(1): 252–256. doi: 10.3969/j.issn.0372-2112.2018.01.035 鲁自清, 姚明, 邓晓华. 关于非相干散射雷达对电离层参数测量仿真[J]. 计算机仿真, 2017, 34(1): 16–19. doi: 10.3969/j.issn.1006-9348.2017.01.004LU Ziqing, YAO Ming, and DENG Xiaohua. Parameters detect simulation of incoherent scatter radar[J]. Computer Simulation, 2017, 34(1): 16–19. doi: 10.3969/j.issn.1006-9348.2017.01.004 LI Lin, CHEN Yajie, JI Hongbing, et al. Research on signal modulation and processing for incoherent scatter radar[C]. International Conference on Information, Communications and Signal Processing, Singapore, 2016: 1–4. LI Lin, LU Yifeng, DING Zonghua, et al. A modified parameter model-based spectrum estimation method for incoherent scatter radar[C]. International Conference on Image, Vision and Computing, Chengdu, China, 2017: 863–867. NYGREN T. Introduction to Incoherent Scatter Measurements[M]. Sodankyla Finland: INVERS OY, 1996: 15–20. 徐彬, 王占阁, 许正文, 等. 基于各向异性分布的非相干散射雷达谱仿真[J]. 空间科学学报, 2017, 37(6): 710–716. doi: 10.11728/cjss2017.06.710XU Bin, WANG Zhange, XU Zhengwen, et al. Simulation of incoherent scatter radar spectra based on inhomogeneous distribution[J]. Chinese Journal of Space Science, 2017, 37(6): 710–716. doi: 10.11728/cjss2017.06.710 SHEFFIELD J. Plasma Scattering of Electromagnetic Radiation[M]. New York: Academic Press, 1975: 113–122. MADSEN K, NIELSEN H B, and TINGLEFF O. Methods for Non-Linear Least Squares Problems[M]. Lyngby: Informatics and Mathematical Modelling Technical University of Denmark, 2004: 17–47. 王存有, 黄张裕, 汪闩林, 等. BP神经网络与多项式拟合在沉降检测中的应用[J]. 地理空间信息, 2017, 15(6): 107–108. doi: 10.3969/j.issn.1672-4623.2017.06.033WANG Cunyou, HUANG Zhangyu, WANG Shuanlin, et al. The application of BP neural network and polynomial fitting in settlement monitoring[J]. Geospatial Information, 2017, 15(6): 107–108. doi: 10.3969/j.issn.1672-4623.2017.06.033 -





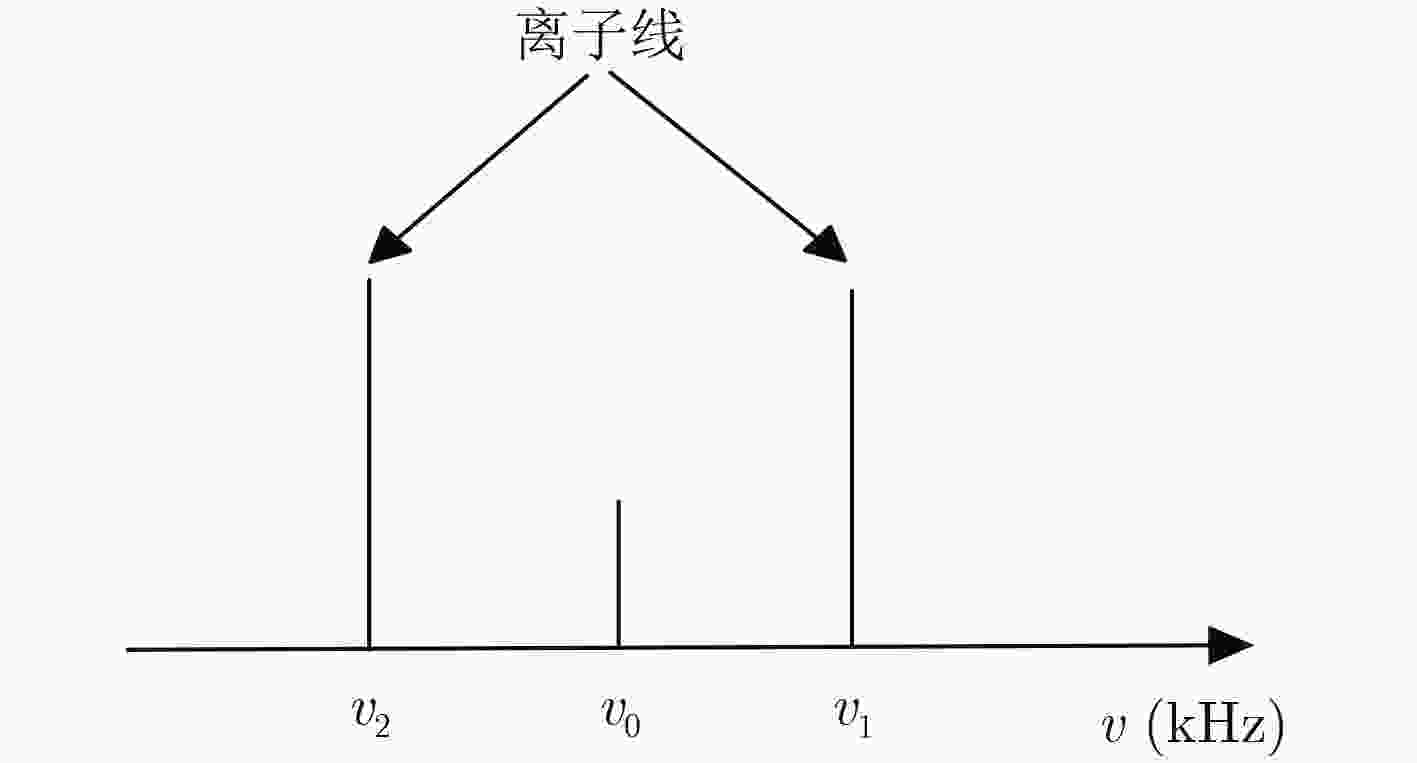
 下载:
下载:
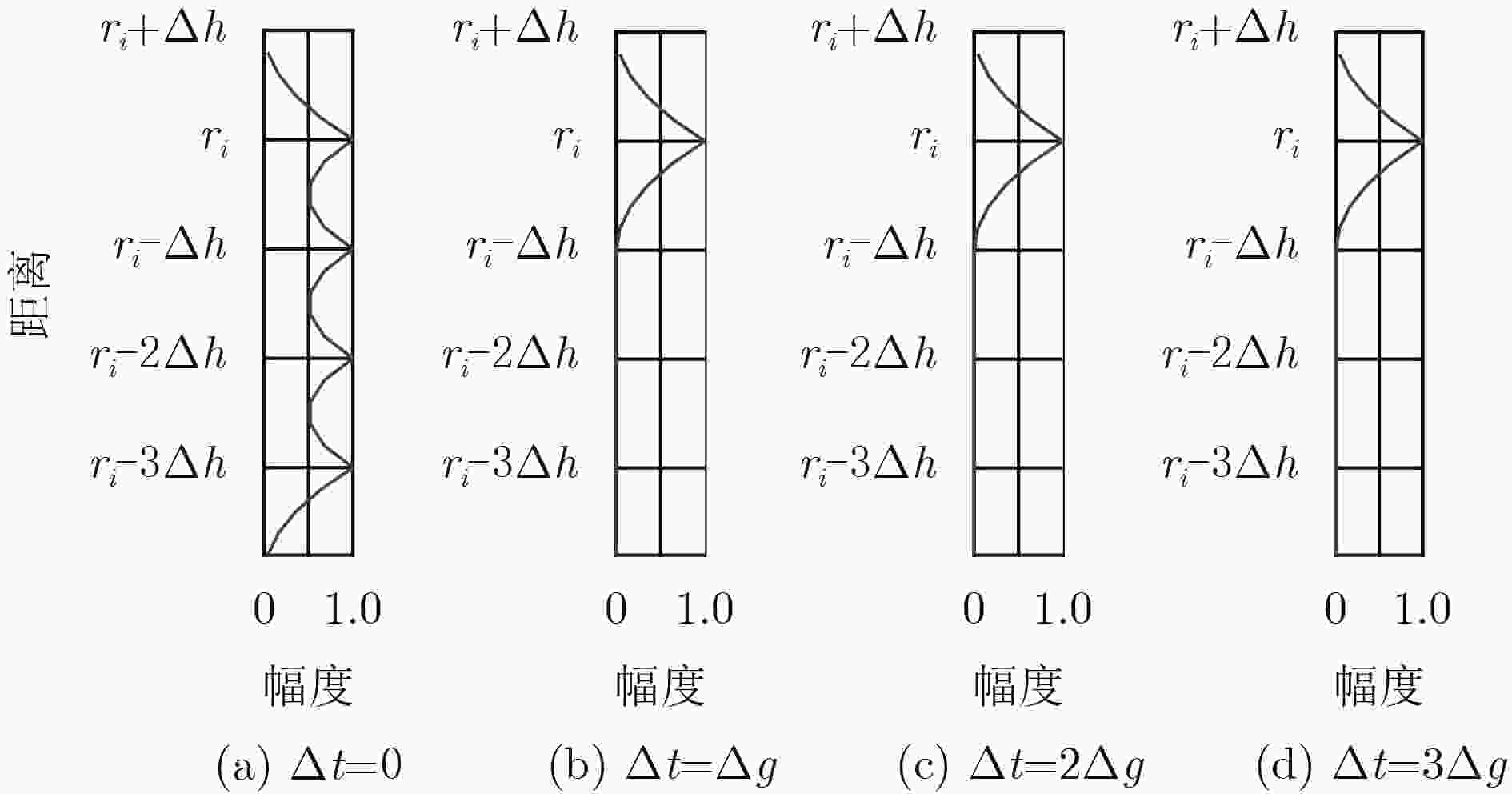

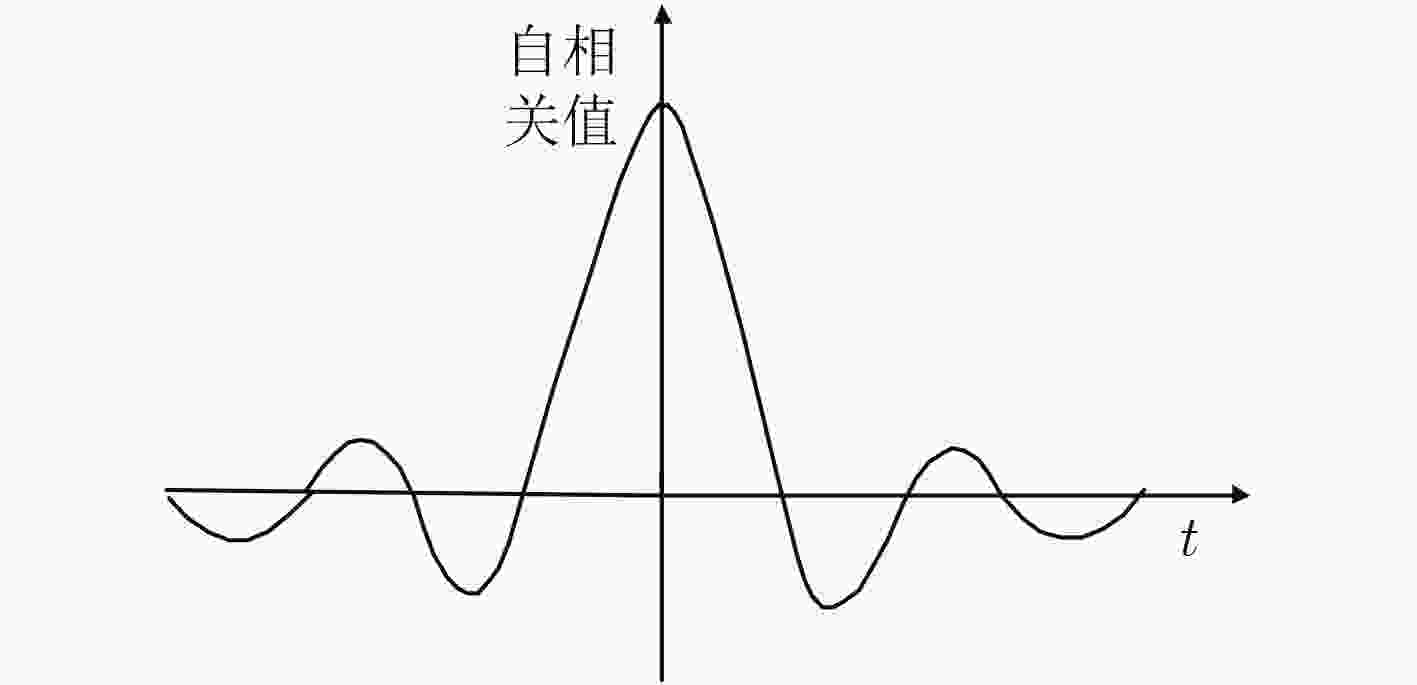
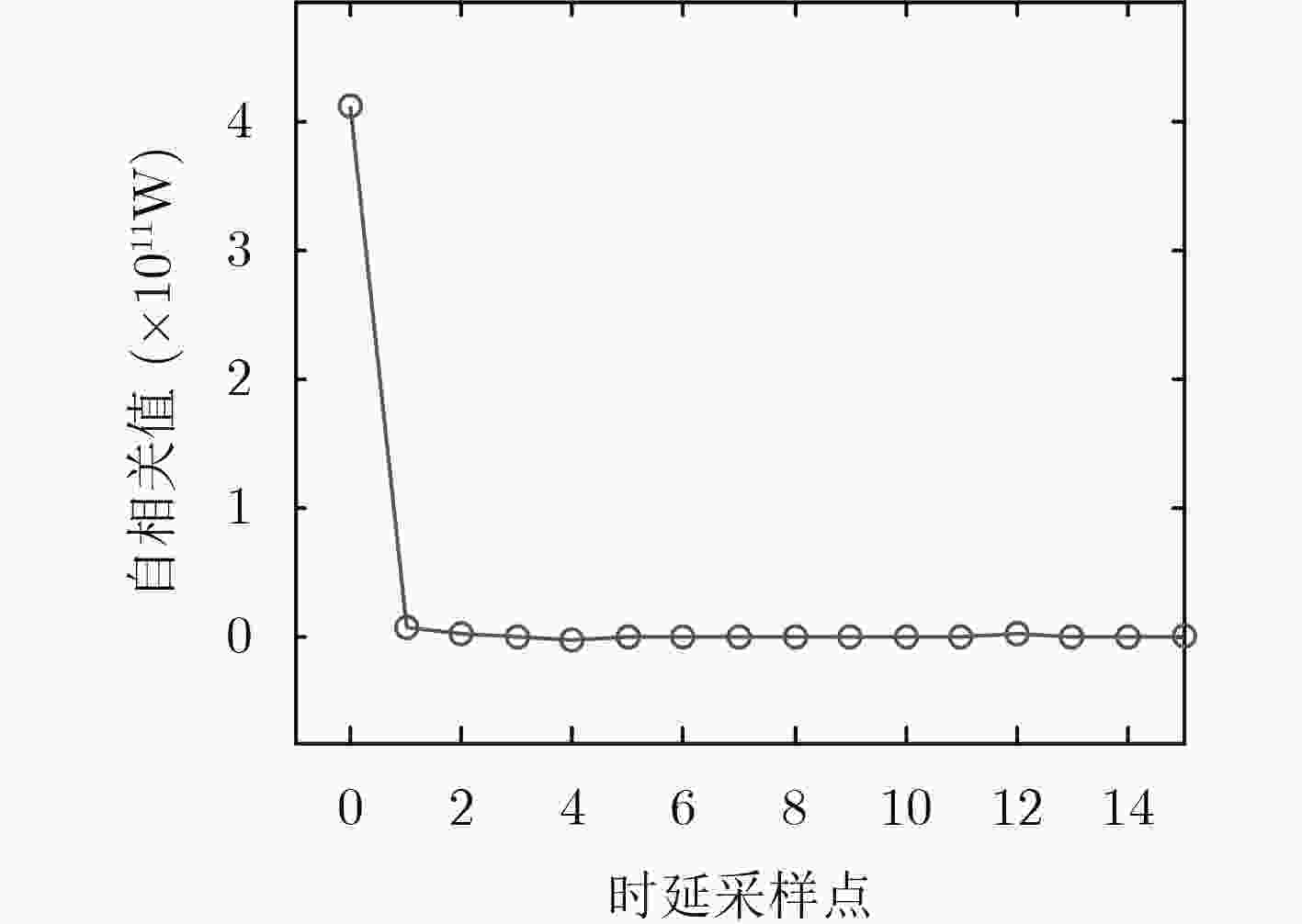



 下载:
下载:
