Anti-bias Track Association Algorithm of Radar and Electronic Support Measurements Based on Track Vectors Detection
-
摘要:
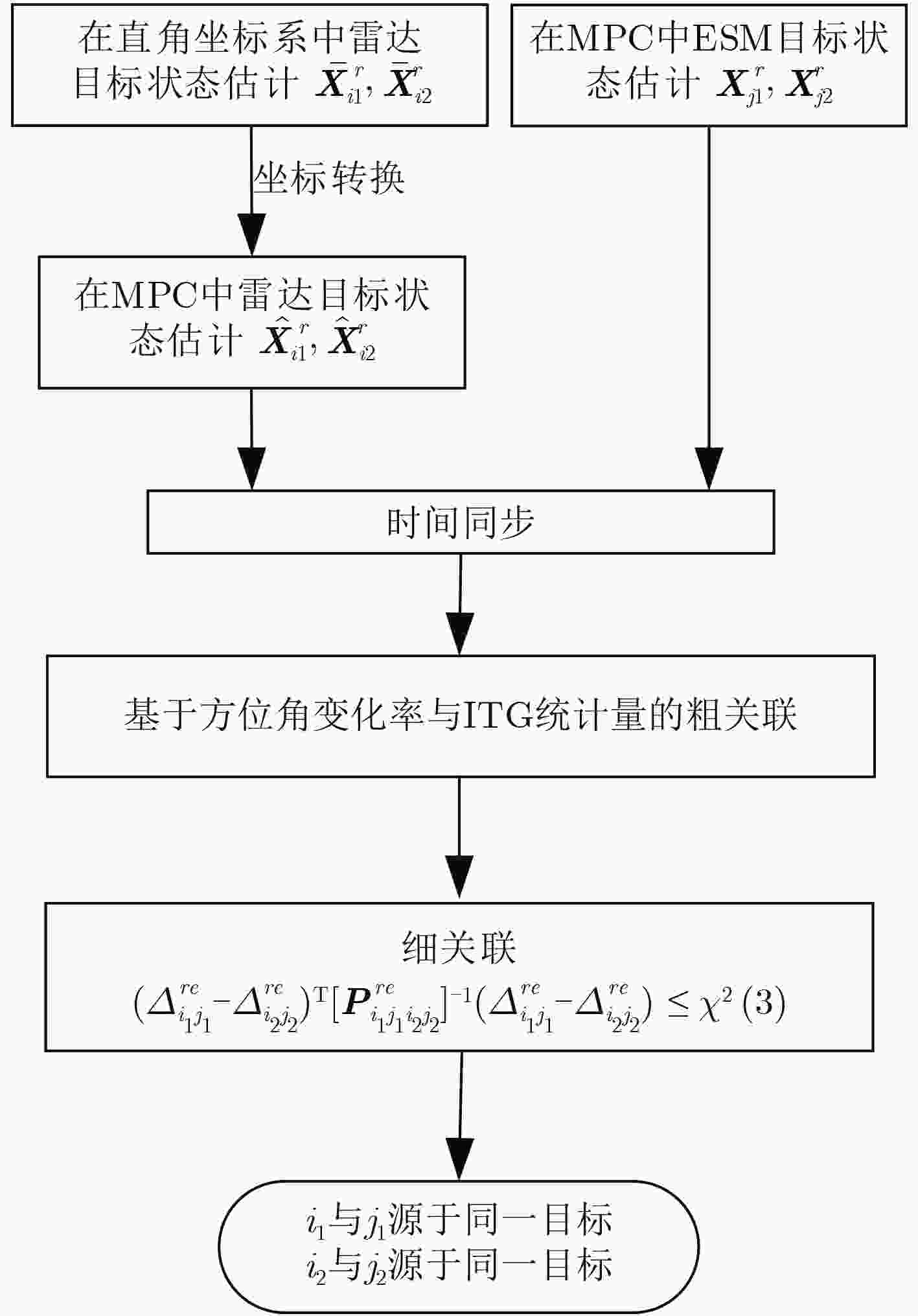
针对雷达与电子支援设施(ESM)存在系统误差、上报目标不完全一致等复杂场景下目标航迹关联问题,该文基于高斯随机矢量统计特性,提出一种基于航迹矢量检测的雷达与ESM航迹抗差关联算法。首先在修正极坐标系(MPC)下推导目标状态估计分解方程,采用真实状态对消的方法得到航迹矢量,为剔除大部分非同源目标航迹,构建方位角变化率-距离变化率与距离比(ITG)统计量进行粗关联,然后采用基于航迹矢量
\begin{document}${\chi ^2}$\end{document} 检验的方法实现雷达与ESM的航迹关联。最后通过实验仿真验证了该文算法在不同系统误差、目标密度、检测概率等环境下的有效性。
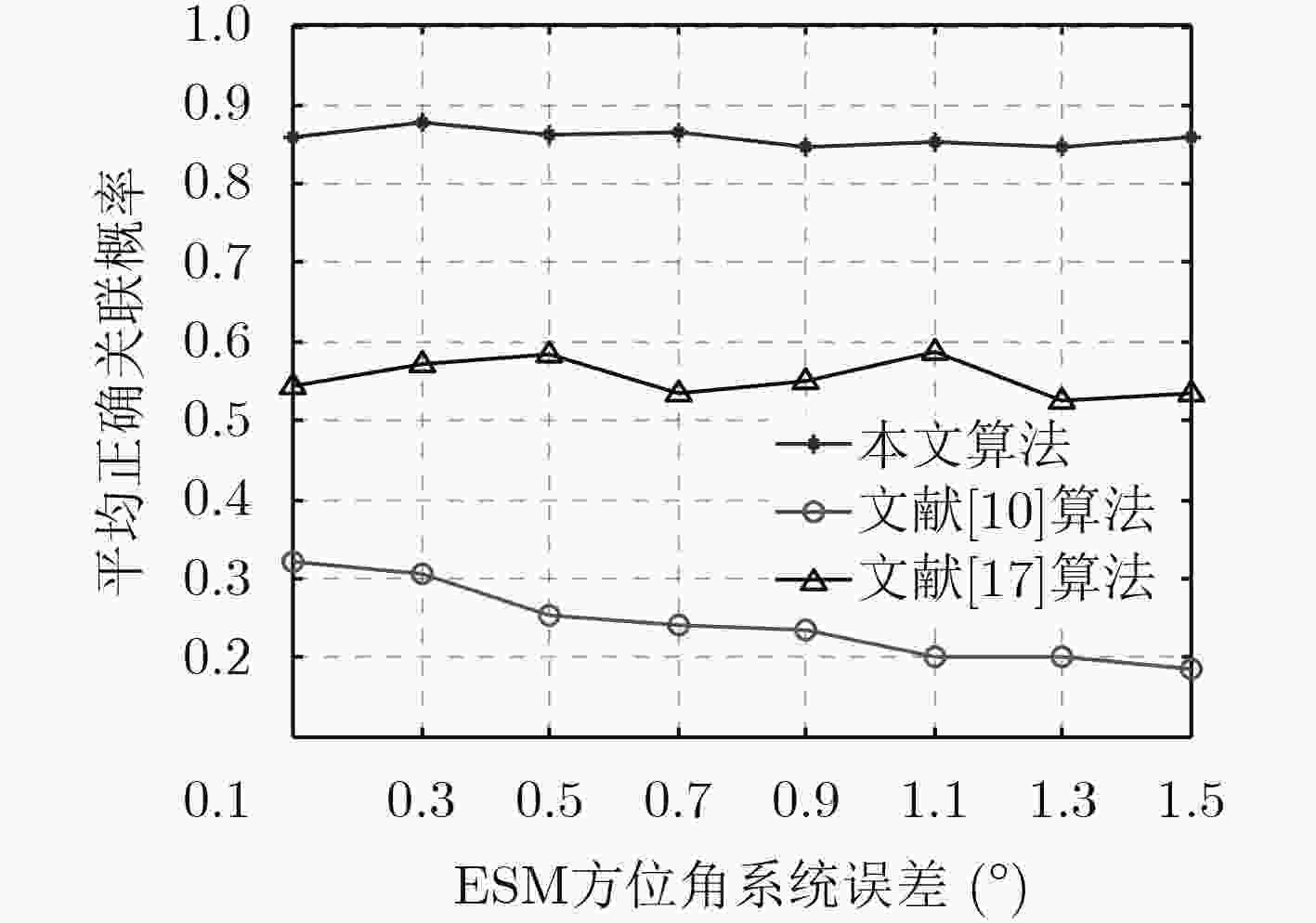
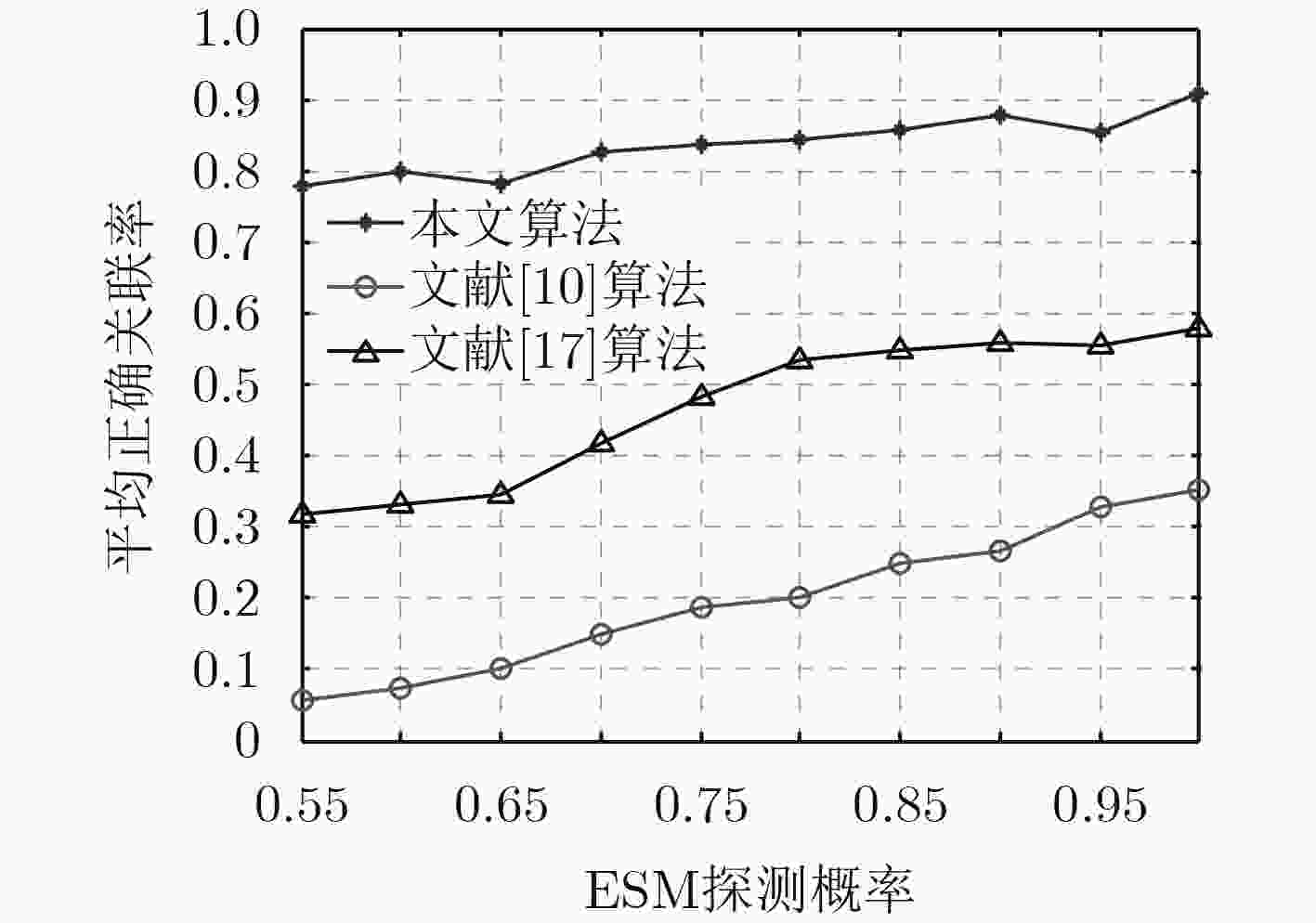
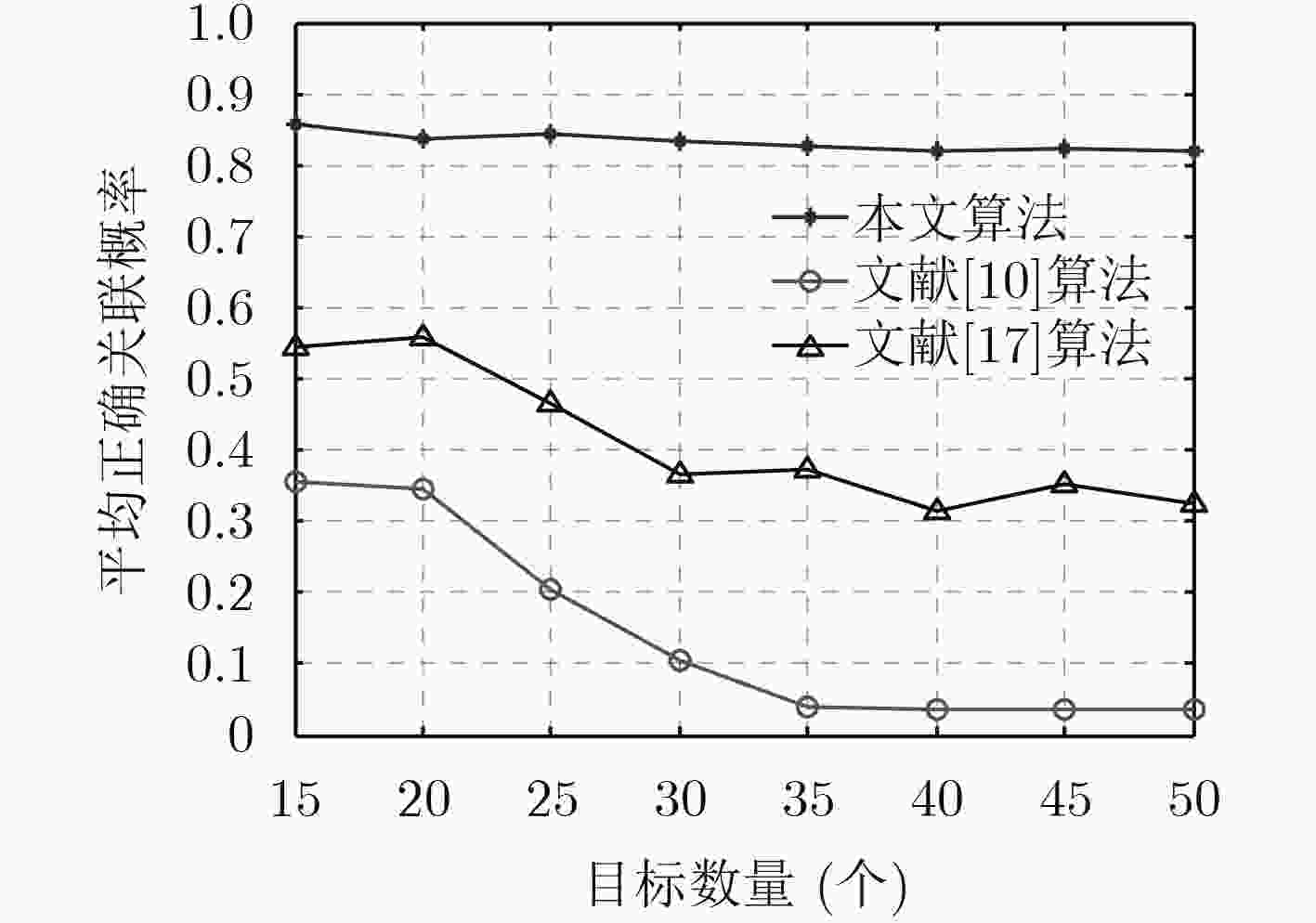
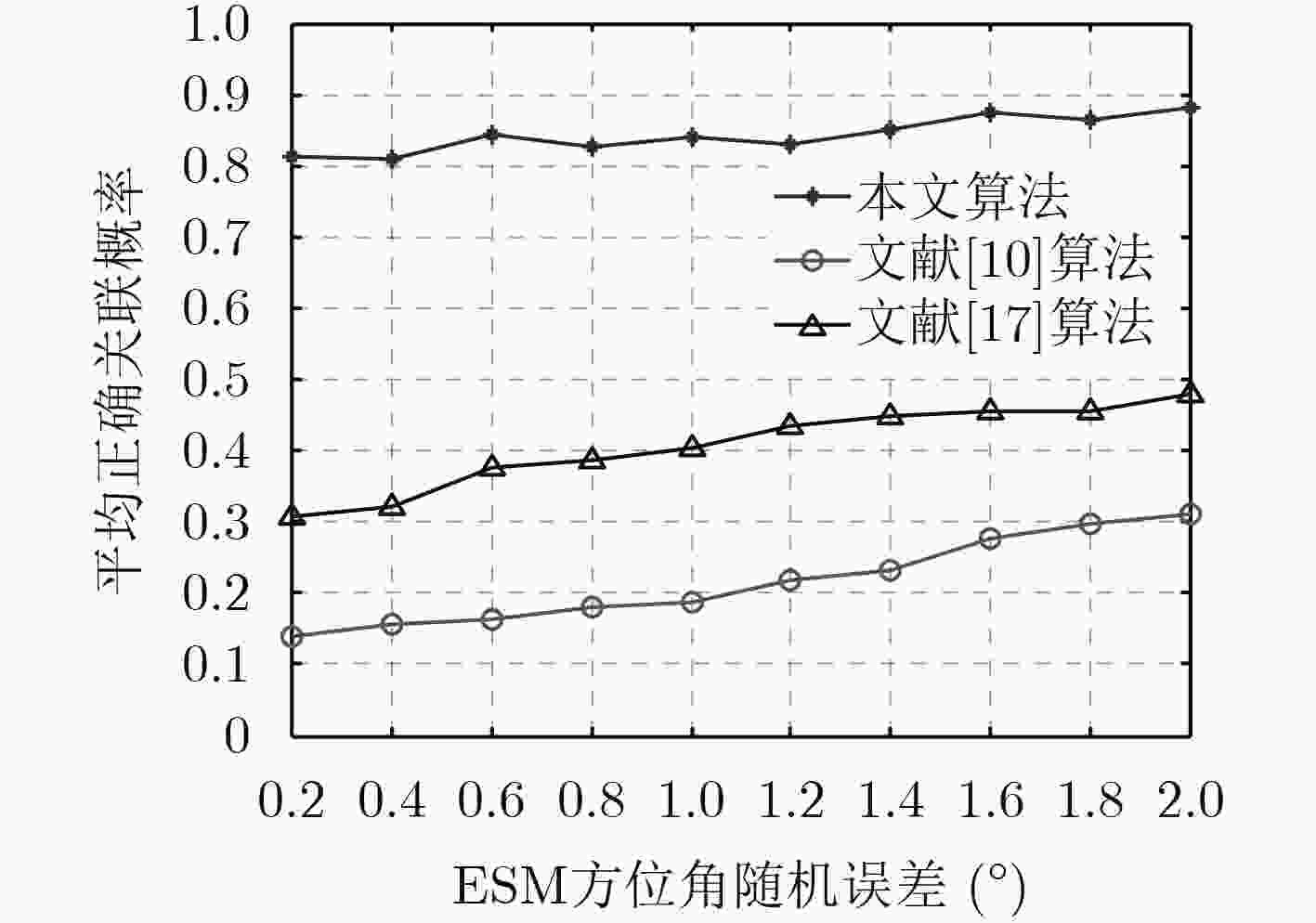
Abstract:To address track-to-track association problem of radar and Electronic Support Measurements (ESM) in the presence of sensor biases and different targets reported by different sensors, an anti-bias track-to-track association algorithm based on track vectors detection is proposed according to the statistical characteristics of Gaussian random vectors. The state estimation decomposition equation is firstly derived in the Modified Polar Coordinates (MPC). The track vectors are obtained by the real state cancellation method. Second, In order to eliminate most non-homologous target tracks, the rough association is performed according to the features of the azimuthal rate and Inverse-Time-to-Go (ITG). Finally, the track-to-track association of radar and ESM is extracted based on track vectors chi-square distribution. The effectiveness of the proposed algorithm are verified by Monte Carlo simulation experiments in the presence of sensor biases, targets densities and detection probabilities.
-
ZHU Hao, WANG Mingliang, Yuen K V, et al. Track-to-track association by coherent point drift[J]. IEEE Signal Processing Letters, 2017, 24(5): 643–647. doi: 10.1109/LSP.2017.2682857 彭彬彬, 关欣. 基于空间分布信息的雷达与ESM航迹灰色关联算法[J]. 电光与控制, 2017, 24(6): 34–38. doi: 10.3969/j.issn.1671-637X.2017.06.007.PENG Binbin and GUAN Xin. Gray track correlation algorithm of radar and ESM based on spatial distribution information[J]. Electronics Optics &Control, 2017, 24(6): 34–38. doi: 10.3969/j.issn.1671-637X.2017.06.007. PENG Binbin and GUAN Xin. A new track association algorithm of radar and ESM[C]. CIE International Conference on Radar, Guangzhou, China, 2016: 1–5. doi: 10.1109/RADAR.2016.8059337. QI Lin, DONG Kai, LIU Yu, et al. Anti-bias track-to-track association algorithm based on distance detection[J]. IET Radar, Sonar & Navigation, 2017, 11(2): 269–276. doi: 10.1049/iet-rsn.2016.0139 李保珠, 董云龙, 李秀友, 等. 基于t分布混合模型的抗差关联算法[J]. 电子与信息学报, 2017, 39(7): 1774–1778. doi: 10.11999/JEIT161084.LI Baozhu, DONG Yunlong, LI Xiuyou, et al. Anti-bias track association algorithm based on t-distribution mixture model[J]. Journal of Electronics &Information Technology, 2017, 39(7): 1774–1778. doi: 10.11999/JEIT161084. TRUNK G V and WILSON J. Association of DF bearing measurements with radar tracks[J]. IEEE Transactions on Aerospace & Electronic Systems, 1987, 23(4): 438–447. doi: 10.1109/TAES.1987.310877 WANG Guohong, HE You, GAO Zhiyong, et al. Improved association of ESM measurements with radar tracks[C]. IET Radar Systems Conference, Edinburgh, UK, 1997: 648–652. doi: 10.1049/cp:19971755. WANG Guohong, MAO Shiyi, HE You, et al. Triple-threshold radar-to-ESM correlation algorithm when each radar track is specified by different number of measurements[J]. IET Radar, Sonar and Navigation, 2000, 147(4): 177–181. doi: 10.1049/ip-rsn:20000094 CHEN Huimin and BAR-SHALOM Y. Track association and fusion with heterogeneous local trackers[C]. IEEE Conference on Decision & Control, New Orleans, USA, 2007: 2675–2680. doi: 10.1109/CDC.2007.4434638. WANG Guohong, ZHANG Xiangyu, and TAN Shuncheng. Effect of biased estimation on radar-to-ESM track association[J]. Journey of System Engineering and Electronic Techniques, 2012, 23(2): 188–194. doi: 10.1109/JSEE.2012.00024 SCALA B F L and FARINA A. Choosing a track association method[J]. Information Fusion, 2002, 3(2): 119–122. doi: 10.1016/S1566-2535(02)00050-7 BENAMEUR K. Radar ESM track to track association[R]. Ottawa: Defence Research Establishment Ottawa, 2001. ZHOU Yifeng, LI Winston, and LEUNG H. Maximum likelihood based ESM/radar track association algorithm in a new modified polar coordinate[R]. Ottawa: Defence Research and Development Canada, 2004. 张翔宇, 王国宏, 王娜, 等. 系统误差下异地配置的雷达和电子支援测量航迹关联[J]. 电光与控制, 2012, 19(3): 30–34.ZHANG Xiangyu, WANG Guohong, WANG Na, et al. Track association of radar and ESM with systematic at different sites[J]. Electronics Optics &Control, 2012, 19(3): 30–34. OFFER C R. Performance of bearing-only ESM-radar tracking association[C]. IET Data Fusion & Target Tracking Conference, London, UK, 2012: 1–6. doi: 10.1049/cp.2012.0409. 关欣, 彭彬彬, 衣晓. 基于区间重合度的雷达与ESM航迹关联算法[J]. 雷达科学与技术, 2017, 15(1): 61–67. doi: 10.3969/j.issn.1672-2337.2017.01.011GUAN Xin, PENG Binbin, and YI Xiao. Track association algorithm of radar and ESM based on the interval overlap ratio[J]. Radar Science and Technology, 2017, 15(1): 61–67. doi: 10.3969/j.issn.1672-2337.2017.01.011 关欣, 彭彬彬, 衣晓. 修正极坐标系下雷达与ESM航迹对准关联[J]. 航空学报, 2017, 38(5): 221–232. doi: 10.7527/S1000-6893.2016.0287GUAN Xin, PENG Binbin, and YI Xiao. Track alignment-association of radar and ESM in MPC[J]. Acta Aeronautics et Astronautics Sinica, 2017, 38(5): 221–232. doi: 10.7527/S1000-6893.2016.0287 何友, 修建娟, 张晶炜, 等. 雷达数据处理及应用[M]. 北京: 电子工业出版社, 2009: 220–223.HE You, XIU Jianjuan, ZHANG Jingwei, et al. Radar Data Processing with Applications[M]. Beijing: Publishing House of Electronics Industry, 2009: 220–223. ZHU Hongyan, WANG Wei, and WANG Chen. Robust track-to-track association in the presence of sensor biases and missed detections[J]. Information Fusion, 2016, 27: 33–40. doi: 10.1016/j.inffus.2015.05.002 -





 下载:
下载:


 下载:
下载:
