Received Signal Strength Indication Difference Location Algorithm Based on Kalman Filter
-
摘要:
针对频谱监测系统中被监测信号无法控制并且没有任何先验知识,只能通过对信号被动监测,即接收与处理信号来估计信号源位置的要求,该文提出一种基于接收信号强度指示差值(RSSID)的定位算法,并利用卡尔曼滤波提高其定位精度。该文将两监测站之间的RSSID转换成信号源到两监测站的距离之比,根据距离之比构造定位方程矩阵,进而利用最小二乘法求取信号源位置。仿真结果表明:所提算法比经典RSSI定位算法性能更优,降低了环境因素对定位精度的影响,并且能更好地满足参数较少的定位服务需求,可以有效地应用于频谱监测系统中。同时,卡尔曼滤波可以有效改善系统的定位精度,达到预期的定位效果。
Abstract:The signal source position can only be estimated by passive monitoring of the signal in terms of that the signal monitored by the spectrum monitoring system can not be controlled and there is no prior knowledge. To address this issue, based on Received Signal Strength Indication Difference (RSSID) and using Kalman filtering, a location algorithm is proposed to improve its localization accuracy. The proposed algorithm transforms the RSSID between two base stations into the ratio of the distance from the location of the signal source to the two base stations, and the distances to construct the matrix of location equations is obtained according to the ratio, and then the least square method to find the signal source position is obtained. The simulation results show that the proposed algorithm has better performance than the classical RSSI localization algorithm, reducing the impact of environmental factors on the positioning accuracy, and better meet the positioning service needing fewer parameters. This algorithm can be effectively applied to the spectrum monitoring system. In addition, Kalman algorithm can effectively improve the system's positioning accuracy, and achieve the expected positioning effect.
-
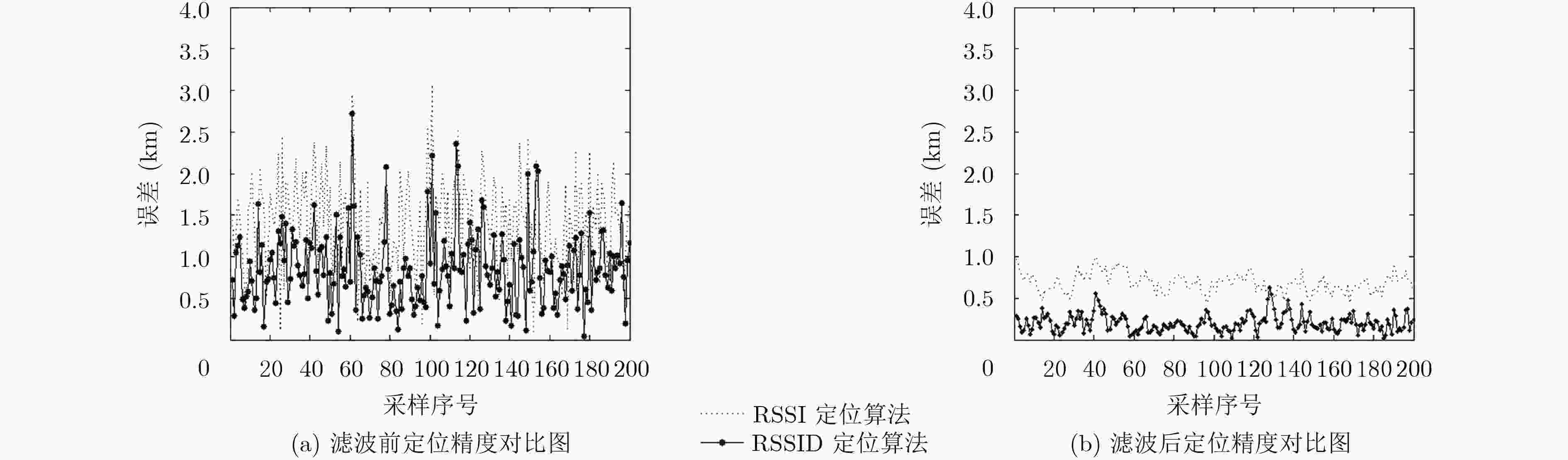
表 1 单目标定位10000次误差统计分析(km)
是否预处理 定位方法 最大误差 最小误差 平均误差 否 RSSI定位 5.0802 0.0239 1.3993 否 RSSID定位 4.6224 0.0076 0.8527 是 RSSI定位 1.4537 0.2273 0.6249 是 RSSID定位 0.8801 0.0068 0.2683 表 2 多目标定位10000次平均误差统计分析(km)
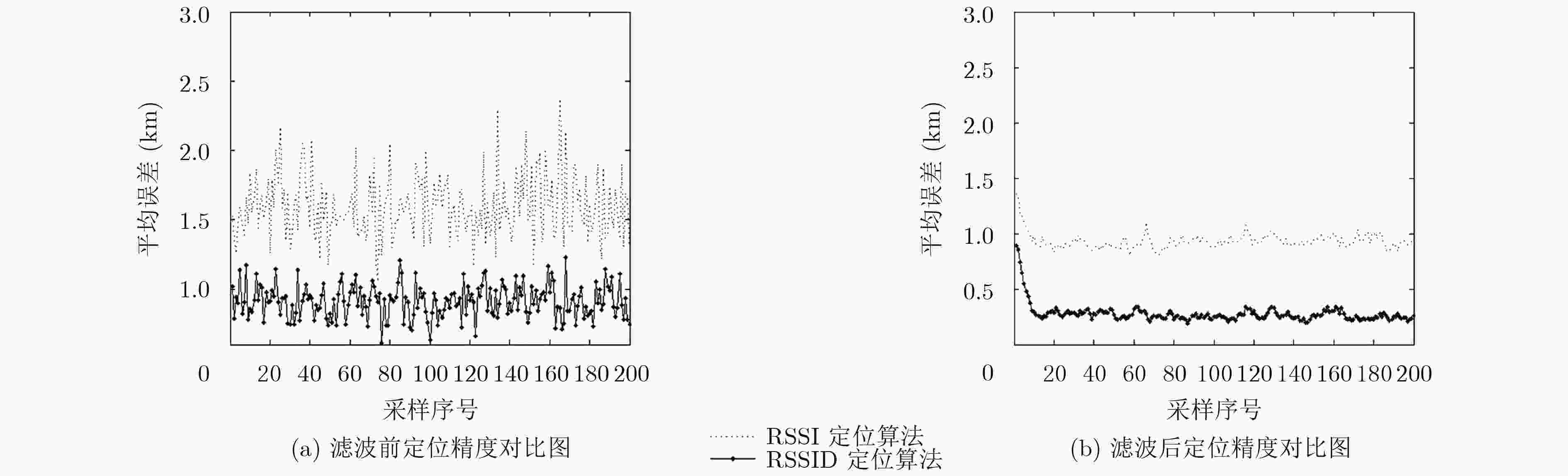
是否预处理 定位方法 最大误差 最小误差 平均误差 否 RSSI定位 1.8602 1.3599 1.5911 否 RSSID定位 1.1015 0.7620 0.9170 是 RSSI定位 1.5312 0.9470 1.1530 是 RSSID定位 0.8284 0.1948 0.2930 -
王先义, 陈丹俊, 刘斌, 等. 复杂电磁环境战场频谱管理[J]. 中国电子科学研究院学报, 2008, 3(4): 338–344. doi: 10.3969/j.issn.1673-5692.2008.04.002WANG Xianyi, CHEN Danjun, LIU Bin, et al. Battlefield spectrum management in complex electromagnetic environment[J]. Journal of China Academy of Electronics and Information Technology, 2008, 3(4): 338–344. doi: 10.3969/j.issn.1673-5692.2008.04.002 史小红. 基于TDOA 的无线定位方法及其性能分析[J]. 东南大学学报(自然科学版), 2013, 43(2): 252–257. doi: 10.3969/j.issn.1001-0505.2013.02.005SHI Xiaohong. TDOA-based wireless positioning method and its performance[J]. Journal of Southeast University (Natural Science Edition) , 2013, 43(2): 252–257. doi: 10.3969/j.issn.1001-0505.2013.02.005 WARNER G A and DOSSO S E. Bowhead whale localization using time-difference-of-arrival data from asynchronous recorders[J]. Journal of the Acoustical Society of America, 2017, 141(3): 1921. doi: 10.1121/1.4978438 WEI Junming and XU Changbin. Improvement of software defined radio based TDOA source localization[C]. Annual Conference of the IEEE Industrial Electronics Society, Dallas, USA, 2015: 5307–5313. LIU Congfeng, YANG Jie, and WANG Fengshuai. Joint TDOA and AOA location algorithm[J]. Journal of Systems Engineering & Electronics, 2013, 24(2): 183–188. doi: 10.1109/JSEE.2013.00023 NOROOZI A. Algebraic solution of source location estimation using TDOA and AOA measurements[C]. Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2017: 1609–1614. 曲付勇, 孟祥伟. 基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J]. 电子与信息学报, 2014, 36(5): 1075–1081. doi: 10.3724/SP.J.1146.2013.01019QU Fuyong and MENG Xiangwei. Source localization using TDOA and FDOA measurements based on constrained total least squares algorithm[J]. Journal of Electronics &Information Technology, 2014, 36(5): 1075–1081. doi: 10.3724/SP.J.1146.2013.01019 LU Zhiyu, BA Bin, WANG Jianhui, et al. A direct position determination method with combined TDOA and FDOA based on particle filter[J]. Chinese Journal of Aeronautics, 2018, 31(1): 161–168. doi: 10.1016/j.cja.2017.11.007 陈淑敏, 乔晓田, 毛佳, 等. 基于接收信号强度(RSSI) 的室内二次定位方法[J]. 传感技术学报, 2015, 28(4): 572–577. doi: 10.3969/j.issn.1004-1699.2015.04.020CHEN Shumin, QIAO Xiaotian, MAO Jia, et al. RSSI-based twice location method for indoor positioning[J]. Chinese Journal of Sensors and Actuators, 2015, 28(4): 572–577. doi: 10.3969/j.issn.1004-1699.2015.04.020 ZHENG Jungang, WU Chengdong, HAO Chu, et al. Localization algorithm based on RSSI and distance geometry constrain for wireless sensor network[C]. IEEE International Conference on Electrical and Control Engineering, Wuhan, China, 2010: 2836–2839. TAZAWA R, HONMA N, MIURA A, et al. RSSI-based localization using wireless beacon with three-element array[J]. IEICE Transactions on Communications, 2018, 101(2). doi: 10.1587/transcom.2017ISP0027 MARC A K J and KAZUNORI O. LRD: A distributed and accurate localization technique for wireless sensors networks[C]. TENCON 2010-2010 IEEE Region 10 Conference, Fukuoka, Japan, 2010: 234–239. 谢树果, 叶知秋, 王磊, 等. 一种基于场强测量的辐射源定位方法[J]. 电波科学学报, 2013, 28(6): 1133–1138. doi: 10.13443/j.cjors.2013.06.024XIE Shuguo, YE Zhiqiu, WANG Lei, et al. Radio source locating method based on signal strength measurement[J]. Chinese Journal of Radio Science, 2013, 28(6): 1133–1138. doi: 10.13443/j.cjors.2013.06.024 卞国龙, 黄海松, 王安忆, 等. 无线传感器网络定位技术的研究[J]. 实验室研究与探索, 2017, 36(6): 122–127. doi: 10.3969/j.issn.1006-7167.2017.06.029BIAN Guolong, HUANG Haisong, WANG Anyi, et al. Research on localization technology of wireless sensor networks[J]. Research and Exploration in Laboratory, 2017, 36(6): 122–127. doi: 10.3969/j.issn.1006-7167.2017.06.029 JUNG J Y, KANG D O, CHOI J H, et al. D2D distance measurement using Kalman filter algorithm for distance-based service in an office environment[C]. International Conference on Advanced Communication Technology (ICACT), Seoul, South Korea, 2015: 221–224. ZHANG Kaibi, ZHANG Yangchuan, and WAN Subo. Research of RSSI indoor ranging algorithm based on Gaussian - Kalman linear filtering[C]. IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi'an, China, 2016: 1628–1632. YU Zongzuo and GUO Gaizhi. Improvement of positioning technology based on RSSI in ZigBee networks[J]. Wireless Personal Communications, 2016, 95(3): 1–20. doi: 10.1007/s11277-016-3860-1 ZHOU Cheng, YUAN Jiazheng, LIU Hongzhe, et al. Bluetooth indoor positioning based on RSSI and Kalman filter[J]. Wireless Personal Communications, 2017, 96(3): 1–16. doi: 10.1007/s11277-017-4371-4 方震, 赵湛, 郭鹏, 等. 基于RSSI测距分析[J]. 传感技术学报, 2007, 20(11): 2526–2530. doi: 10.3969/j.issn.1004-1699.2007.11.037FANG Zhen, ZHAO Zhan, GUO Peng, et al. Analysis of distance measurement based on RSSI[J]. Chinese Journal of Sensors and Actuators, 2007, 20(11): 2526–2530. doi: 10.3969/j.issn.1004-1699.2007.11.037 -





 下载:
下载:


 下载:
下载:
