Research on Placement Algorithm of Service Function Chaining Oriented to Software Defined Networking
-
摘要:
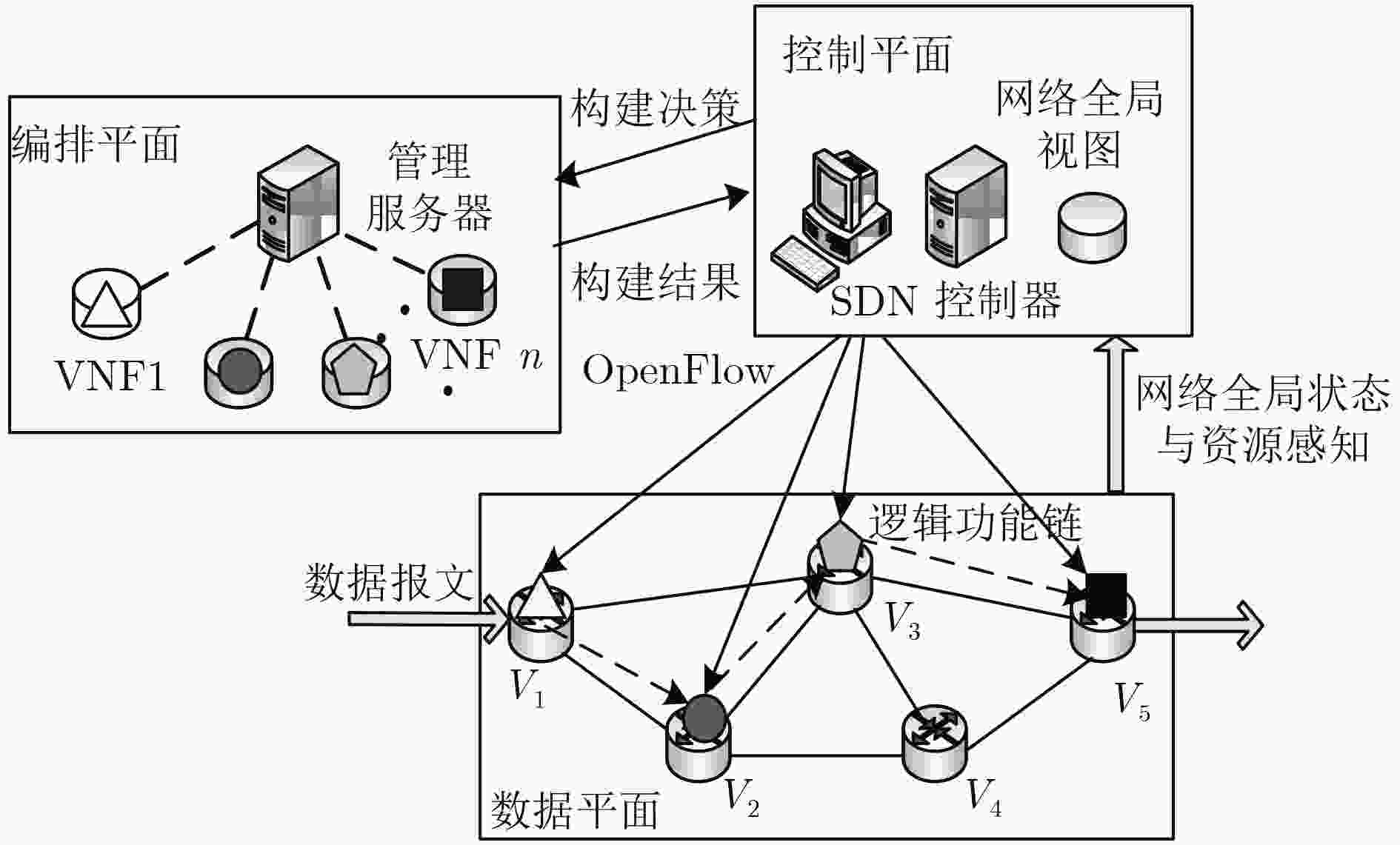
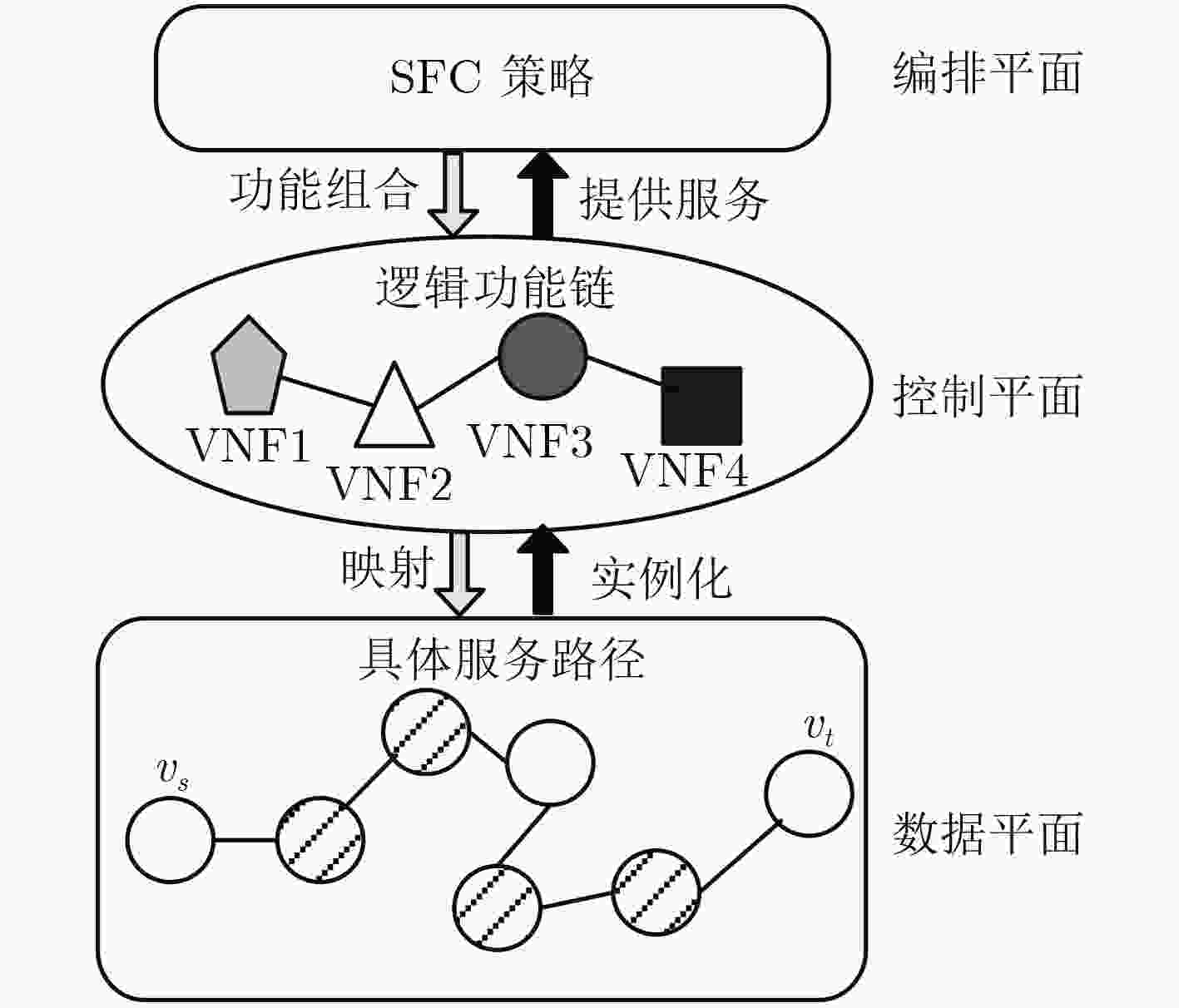
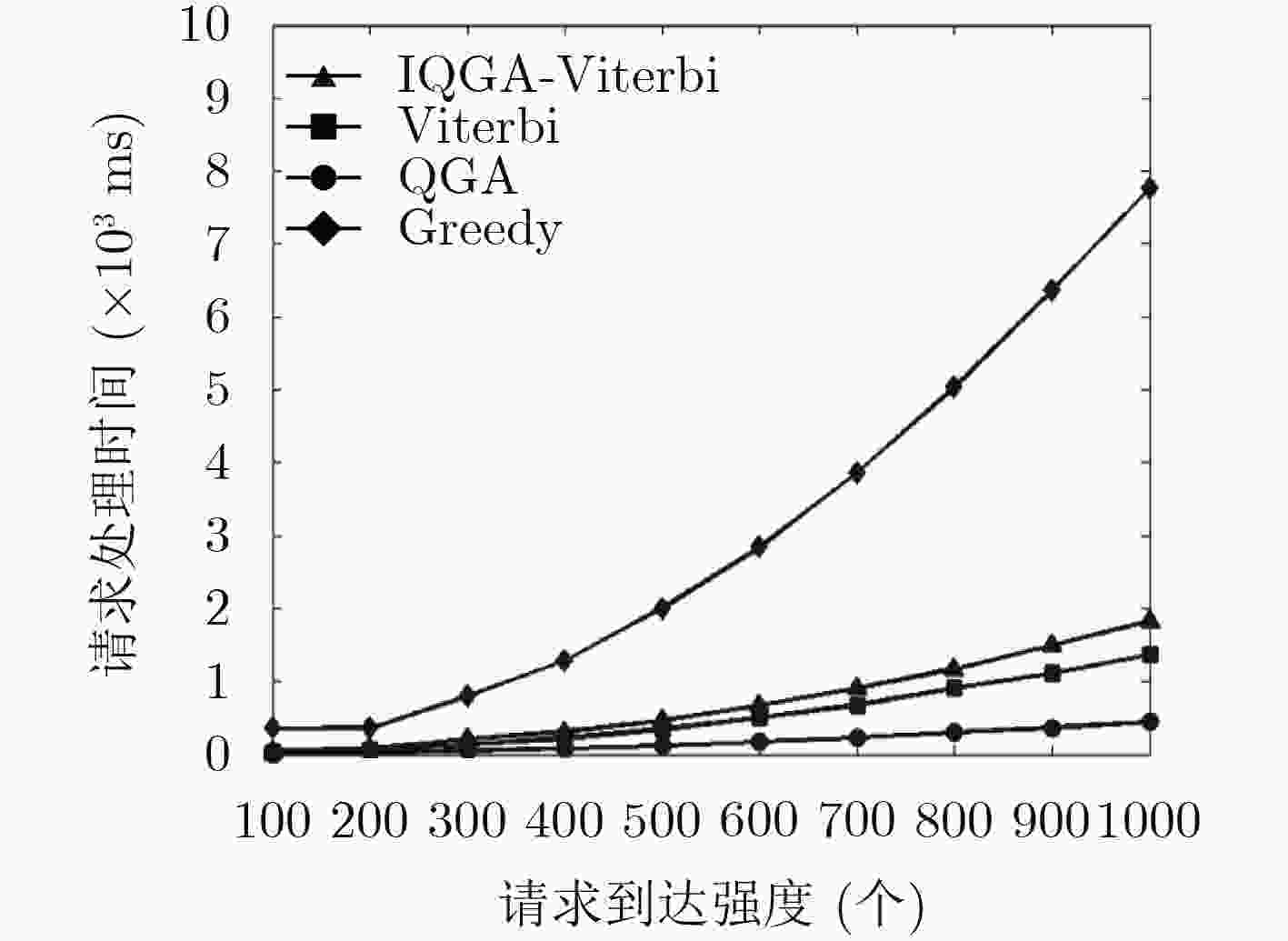
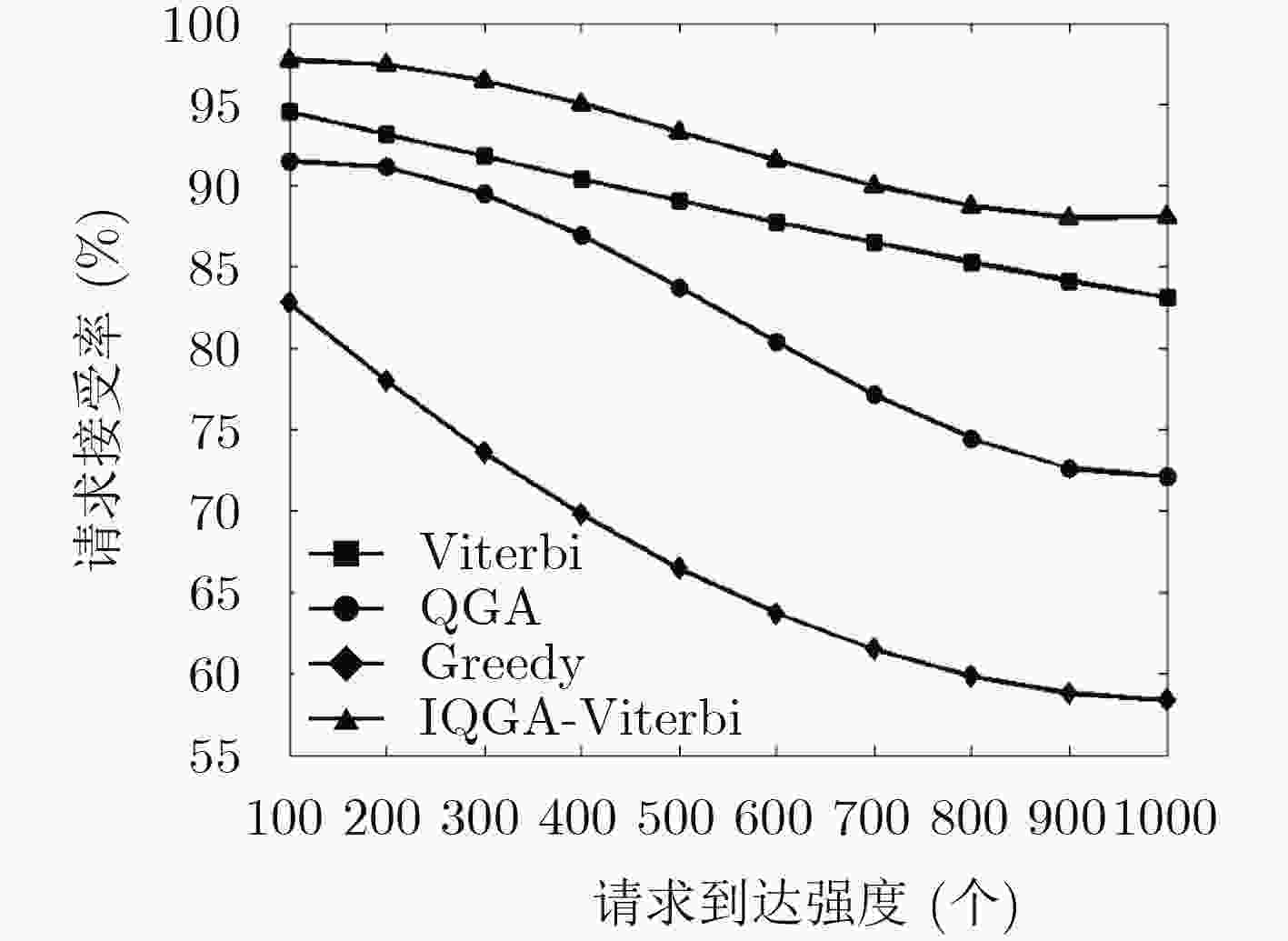
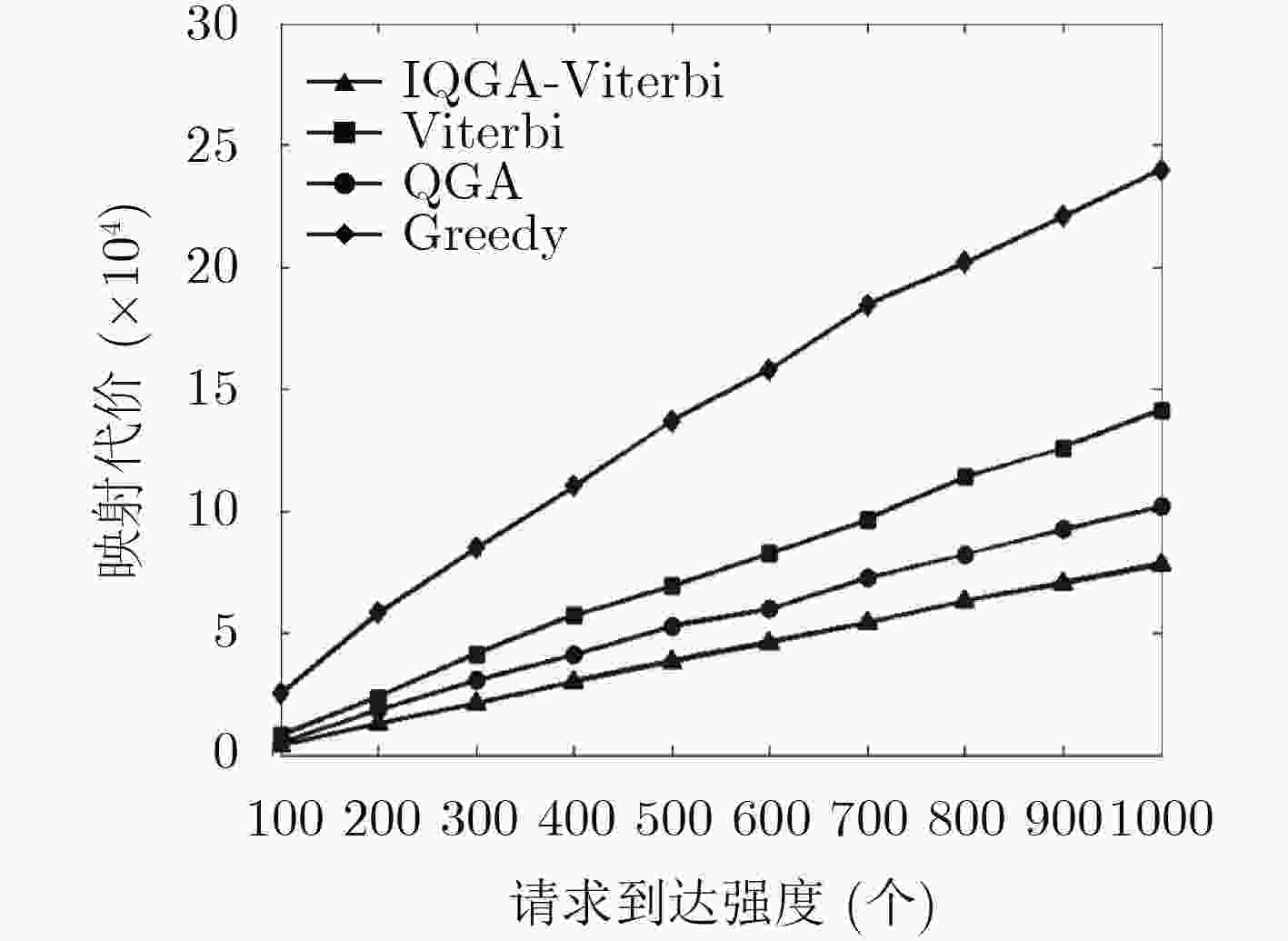
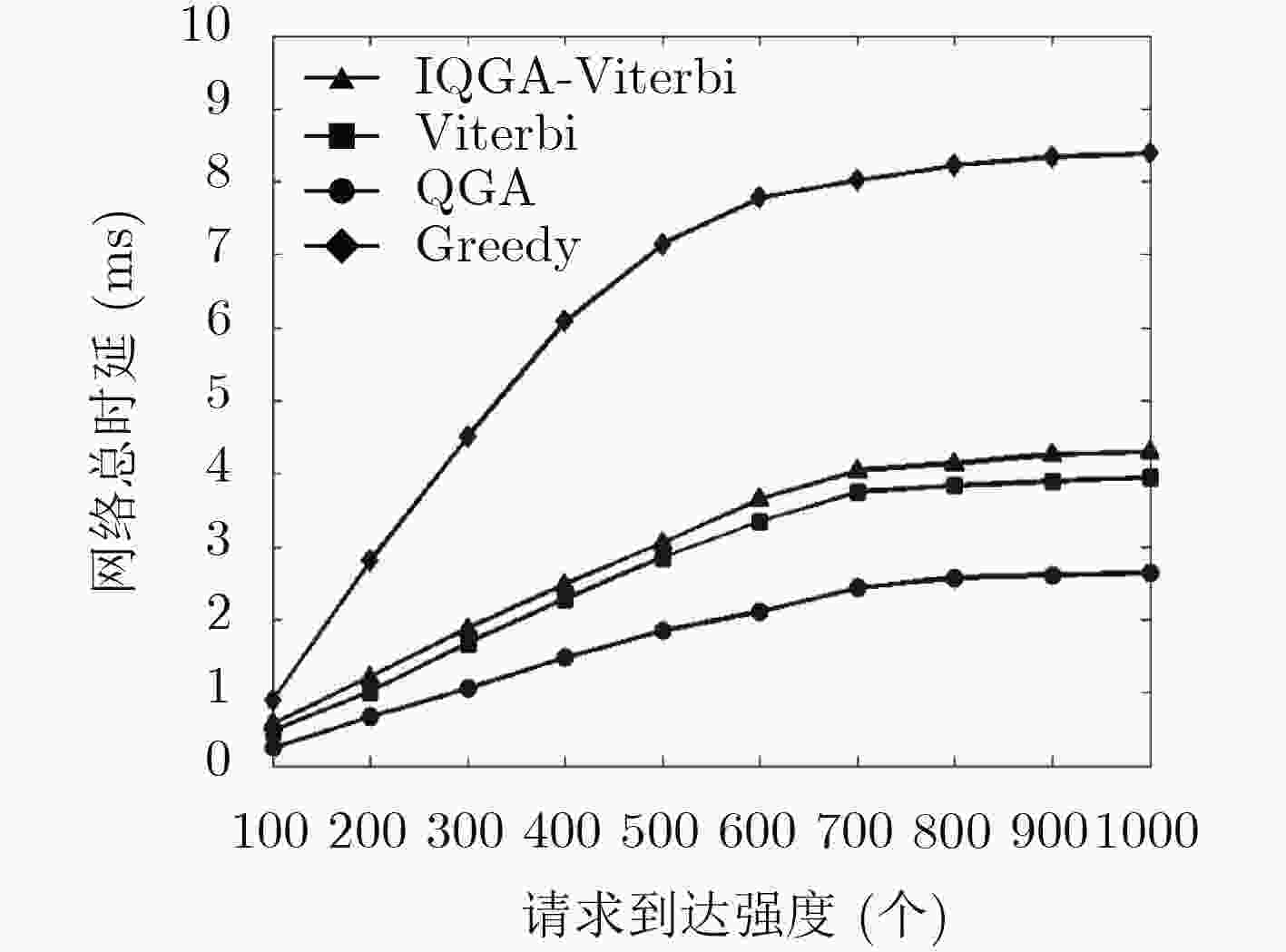
针对网络功能虚拟化(NFV)环境下,现有服务功能链部署方法无法在优化映射代价的同时保证服务路径时延的问题,该文提出一种基于IQGA-Viterbi学习算法的服务功能链优化部署方法。在隐马尔可夫模型参数训练过程中,针对传统Baum-Welch算法训练网络参数容易陷入局部最优的缺陷,改进量子遗传算法对模型参数进行训练优化,在每一迭代周期内通过等比例复制适应度最佳种群的方式,保持可行解多样性和扩大空间搜索范围,进一步提高模型参数的精确度。在隐马尔科夫链求解过程中,针对隐含序列无法直接观测这一难点,利用Viterbi算法能精确求解隐含序列的优势,解决有向图网络中服务路径的优化选择问题。仿真实验结果表明,与其它部署算法相比,所提IQGA-Viterbi学习算法能有效降低网络时延和映射代价的同时,提高了网络服务的请求接受率。
Abstract:For Network Function Virtualization (NFV) environment, the existing placement methods can not guarantee the mapping cost while optimizing the network delay, a service function chaining optimal placement algorithm is proposed based on the IQGA-Viterbi learning algorithm. In the training process of Hidden Markov Model (HMM) parameters, the traditional Baum-Welch algorithm is easy to fall into the local optimum, so the quantum genetic algorithm is proposed, which can better optimize the model parameters. In each iteration, the improved algorithm maintains the diversity of feasible solutions and expands the scope of the spatial search by replicating the best fitness population with equal proportion, thus improving the accuracy of the model parameters. In the process of solving Hidden Markov chain, to overcome the problem that can not be directly observed for hidden sequences, Viterbi algorithm can solve the implicit sequences exactly and solve the problem of optimal service paths in the directed graph. Experimental results show that the network delay and mapping costs are lower compared with the existing algorithms. In addition, the acceptance ratio of requests is raised.
-
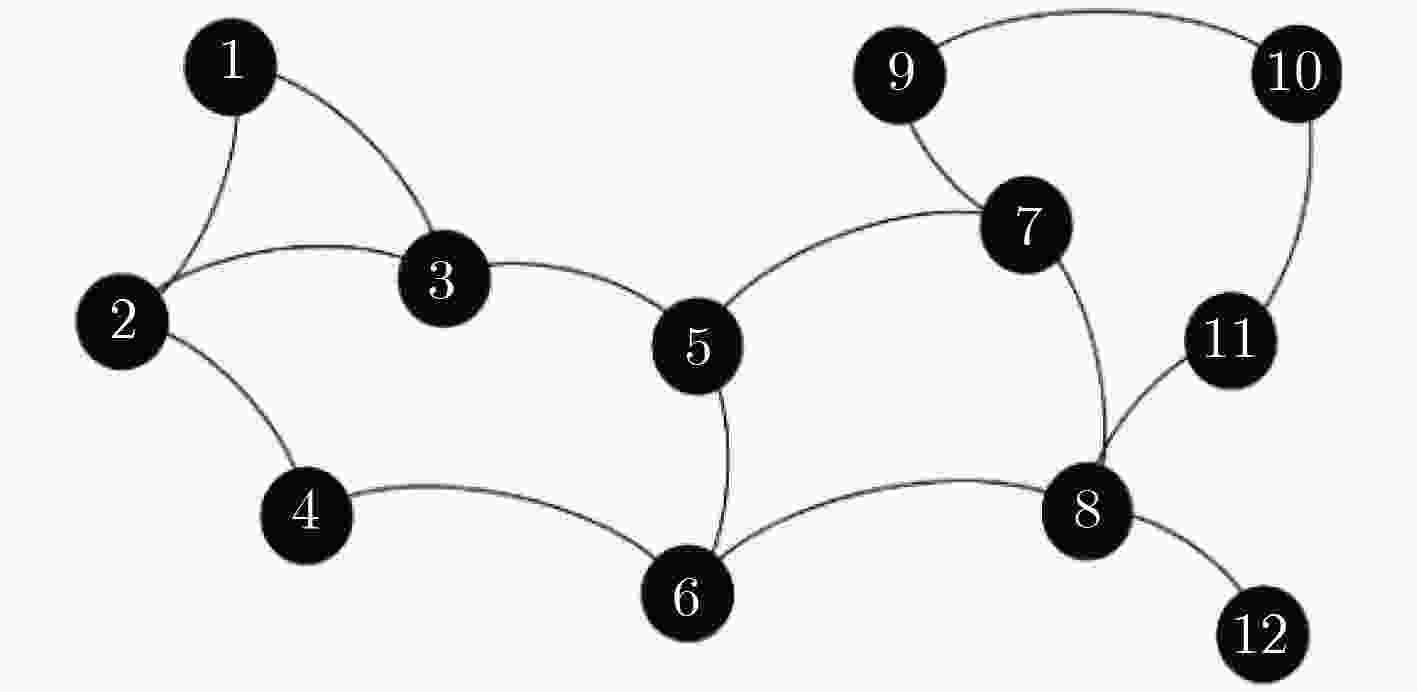
表 1 IQGA-Viterbi学习算法具体过程
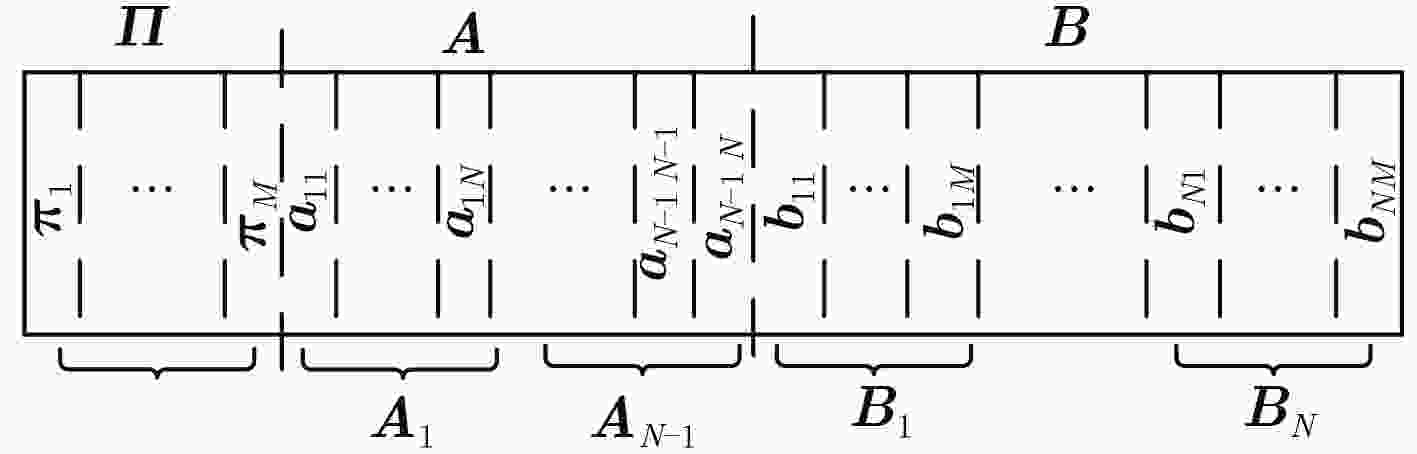
输入:服务请求序列O,底层网络初始参数${{λ}}$0 输出:最小化开销部署策略 $\pi_s$ 步骤 1 IQGA算法初始化。设置训练所用的观测序列O数目为K,将底层初始网络参数编码成种群大小为M、量子比特编码长度为N的染
色体。记迭代次数t的种群$P(t)=\left\{C^{(t)}_1,C^{(t)}_2,·\!·\!·,C^{(t)}_M \right\}$,其中种群个体C(t) M(m=1,2,···,M)的量子比特表示,初始状态的网络参数
可表示为如式(4)。
${C} _m^{(0)} = \left[ {\begin{array}{*{20}{c}} {\alpha _{m1}^{(0)}} \\ {\beta _{m1}^{(0)}} \end{array}\left| {\begin{array}{*{20}{c}} {\alpha _{m2}^{(0)}} \\ {\beta _{m2}^{(0)}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {·\!·\!· } \\ {·\!·\!· } \end{array}} \right.\left| {\begin{array}{*{20}{c}} {\alpha _{mN}^{(0)}} \\ {\beta _{mN}^{(0)}} \end{array}} \right.} \right] = \left[ {\begin{array}{*{20}{c}} {{1 / {\sqrt 2 }}} \\ {{1 / {\sqrt 2 }}} \end{array}\left| {\begin{array}{*{20}{c}} {{1 / {\sqrt 2 }}} \\ {{1 / {\sqrt 2 }}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {·\!·\!· } \\ {·\!·\!· } \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{1 / {\sqrt 2 }}} \\ {{1 / {\sqrt 2 }}} \end{array}} \right.} \right],\ m = 1,2,·\!·\!· ,M$ (4)步骤 2 种群P(t)复制、变异和选择。对于种群P(t)进行等比例复制生成P$\,'$(t),利用高斯变异的操作对种群P$\,'$(t)进行更新,并生成种群
P$\,''$(t),通过选择等比例压缩P$\,''$(t)生成P(t+1)。步骤 3 评价种群P(t+1)。对于经选择后种群P(t+1)中个体的量子位进行测量,随机生成[0, 1]的随机数,若该随机数大于或等于${\left| \alpha \right|^2}$或
${\left| \beta \right|^2}$,则测量的结果取值为1,否则取0。该过程是得到每个个体测量后的状态${{{X}}_{C} } = \left\{ {{{x} _1},{{x} _2},·\!·\!· ,{{x} _{N} }} \right\}$,并将其转化为十进制数,代
入目标函数如式(5)。
${\rm{Fitness} }({X_C}) = \frac{1}{K}\sum\limits_{k = 0}^K {\frac{1}{{{{{C}}^{(k)}}}}} $ (5)步骤 4 更新重估计开销值${\widehat {{a}}_{ij}}$, ${\widehat {{b}}_{ik}}$。记录并保存当前迭代次数t的最佳个体,以及其对应的开销数值矩阵${\widehat {{A}}_{n \times n}}$和${\widehat {{B}}_{m \times n}}$,据此更新模型重估
参数${\widehat {{a}}_{ij}}$, ${\widehat {{b}}_{ik}}$,在迭代次数t+1时更新网络底层视图,并继续对底层网络参数反复迭代、重估。采用最大进化迭代次数Max_step作
为算法的终止条件,判断是否到达最大进化迭代次数,若是则终止进化后得到一组最优的网络底层参数${{λ}}$=(A,B,${{Π}}$),否则返回
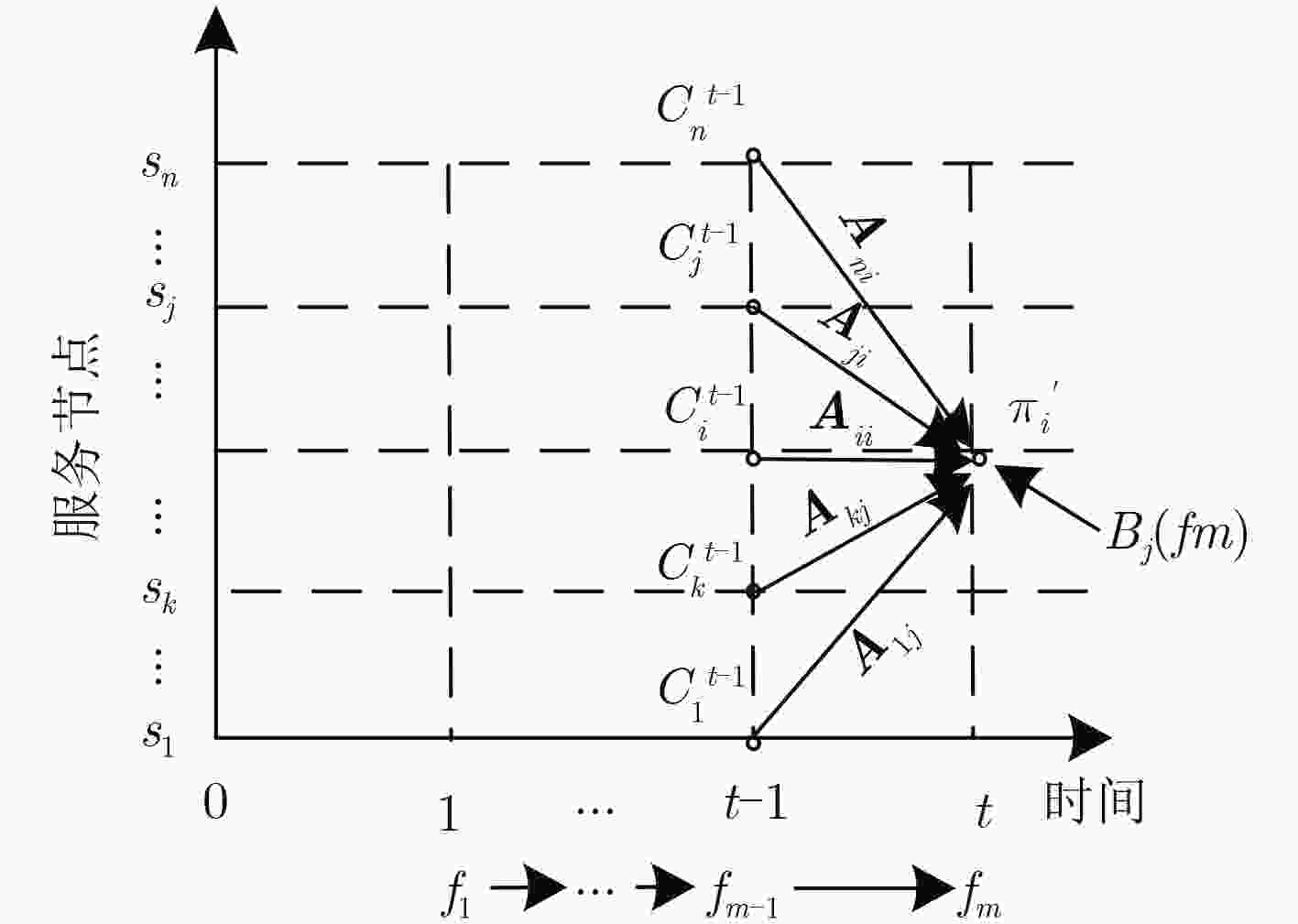
至步骤2继续迭代。步骤 5 Viterbi算法参数初始化。将IQGA算法得到${{λ}}$=(A,B,${{Π}}$)和观测序列O作为Viterbi的输入。 步骤 6 Viterbi变量${\delta _t}({j} )$递推。从源端节点${{{v}}_{{s}}}$开始,根据服务链中VNF编排顺序${\varphi _l}$,在每个迭代周期内计算从服务节点si到候选节点sj的最
小开销,即Viterbi变量${\delta _t}\left( {j} \right) = \min \left[ {{{A}}\left( {{{s} _i},{{s} _j}} \right) + {{B}}\left( {{{s} _j},{{f} _m}} \right)} \right]$的计算,按照式(6)的递推方式,搜索整个观察序列O条件下的具体服务
路径S,直到最后流出目的节点${{{v}}_t}$。位于不同时刻的部署开销值,取其中最小值,进而得到最小开销服务路径的函数值$\min {\delta _t}({f_m})$。
$\left. \begin{aligned}{{{d}}_{{{{t}}_1}}}({{{f}}_{{1}}})=& {{d}}({{{s}}_1}) \\ {{{d}}_{{{{t}}_2}}}({{{f}}_2})=&{{ \min}}\left\{ {{{{d}}_{{{{t}}_1}}}({{{f}}_1}) + {{A}}({{{s}}_1}{{,}}{{{s}}_k}) + {{B}}({{{s}}_k}{{,}}{{{f}}_2})} \right\} \\ & \vdots \\ {{{d}}_{{t_m}}}({{{f}}_m})=&{{\min}}\left\{ {{{{d}}_{{{t - 1}}}}({{{f}}_{{{m - 1}}}}) + {{A}}({{{s}}_{{j}}}{{,}}{{{s}}_{{n}}}) + {{B}}({{{s}}_{{n}}}{{,}}{{{f}}_m})} \right\}\end{aligned}\right\} $ (6)步骤7 标记函数${\varphi _t}({{i}})$回溯。记录位于当前时刻最小开销序列应选取的前一时刻部署服务节点,利用标记函数${\varphi _t}\left( {i} \right) = \arg \min \left[ {{A}}\left( {{{s} _i},{{s} _j}} \right)\right. $
$ \left.+ {{B}}\left( {{{s} _j},{{f} _m}} \right) \right]$依次回溯,以服务链l 中最后一个VNF节点选取开销最小时所选择的服务节点sn为起点,沿着函数${{{s}}_{i - 1}} = {\varphi _t}({{{s}}_i})$给出
上一时刻所选择的服务节点,直到计算出s1,得到开销最小状态序列路径,并输出服务路径的构造方案${\pi _{{s}}}{{ = }}\left\{ {{\pi _{{{{f}}_1}}}{{,}}{\pi _{{{{f}}_2}}}{{,}}·\!·\!· {{,}}{\pi _{{{{f}}_m}}}} \right\}$。表 2 算法测试结果统计与比较
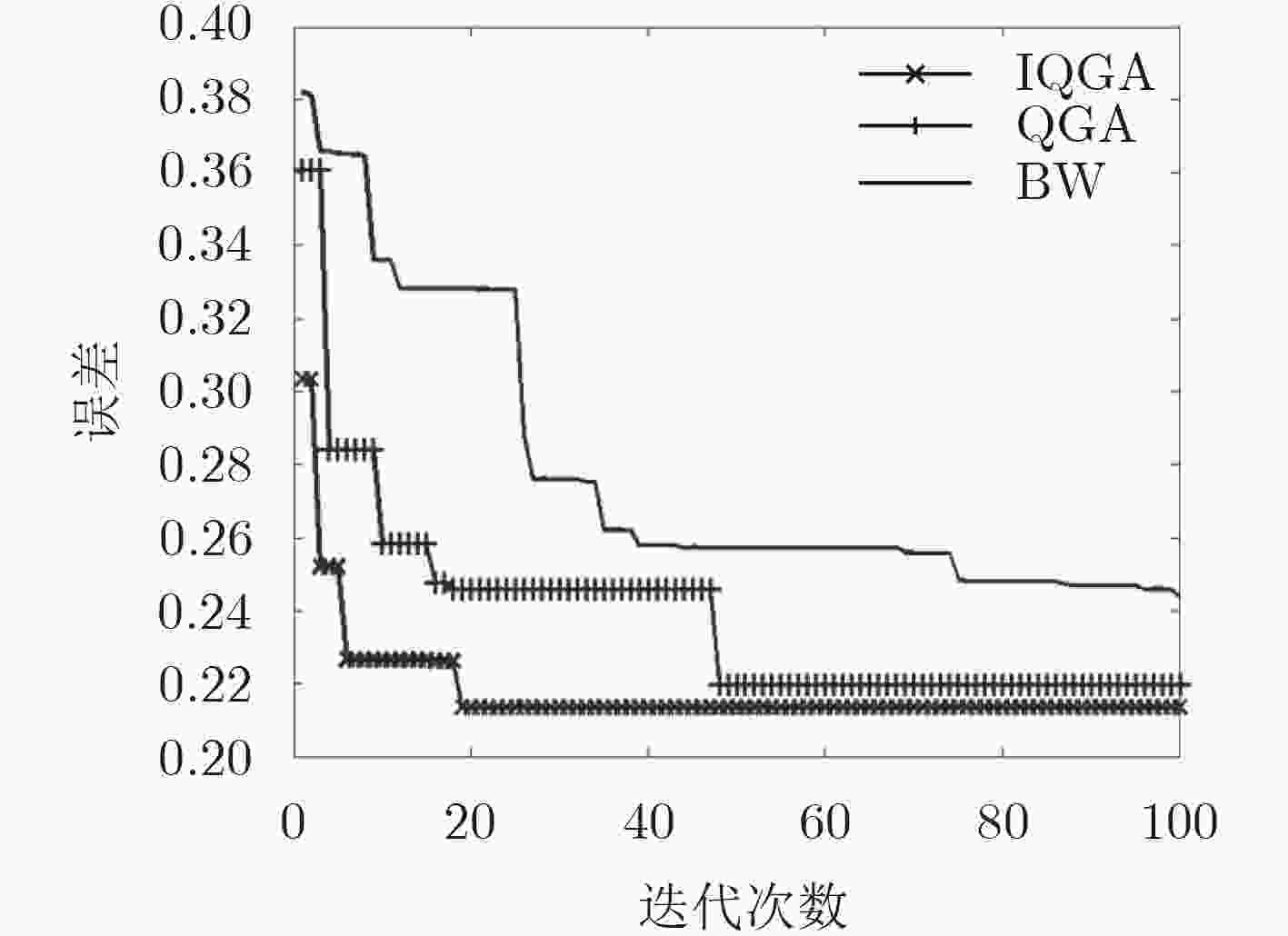
算法 误差最小值 平均迭代数 IQGA 0.214 20 QGA 0.223 48 BW 0.248 76 -
BHAMARE D, JAIN R, SAMAKA M, et al. A survey on service function chaining[J]. Journal of Network & Computer Applications, 2016, 75(C): 138–155. doi: 10.1016/j.jnca.2016.09.001 MEDHAT A and TALEB T. Service function chaining in next generation networks: State of the art and research challenges[J]. IEEE Communications Magazine, 2017, 55(2): 216–223. doi: 10.1109/mcom.2016.1600219rp MCKEOWN N, ANDERSON T, BALAKRISHNAN H, et al. OpenFlow: Enabling innovation in campus networks[J]. ACM SIGCOMM Computer Communication Review, 2008, 38(2): 69–75. doi: 10.1145/1355734 HAN Bo, GOPALAKRISHNAN V, JI Lusheng, et al. Network function virtualization: Challenges and opportunities for innovations[J]. IEEE Communications Magazine, 2015, 53(2): 90–97. doi: 10.1109/mcom.2015.7045396 KIM S, PARK S, KIM Y, et al. VNF-EQ: Dynamic placement of virtual network functions for energy efficiency and QoS guarantee in NFV[J]. Cluster Computing, 2017, 20(3): 1–11. doi: 10.1007/s10586-017-1004-3 BHAMARE D, SAMAKA M, ERBAD A, et al. Optimal virtual network function placement in multi-cloud service chaining architecture[J]. Computer Communications, 2017, 102(C): 1–16. doi: 10.1016/j.comcom.2017.02.011 BARI M F, CHOWDHURY S R, AHMED R, et al. On orchestrating virtual network functions[C]. International Conference on Network and Service Management, Barcelona, Spain, 2015: 50–56. doi: 10.1109/cnsm.2015.7367338. XIONG Gang, Hu Yuxiang, TIAN Le, et al. A virtual service placement approach based on improved quantum genetic algorithm[J]. Information and Electronic Engineering Frontiers, 2016, 17(7): 661–671. doi: 10.1631/fitee.1500494 LUKOVSZKI T, ROST M, and SCHMID S. It’s a match!: Near-optimal and incremental middlebox deployment[J]. ACM SIGCOMM Computer Communication Review, 2016, 46(1): 30–36. doi: 10.1145/2875951.2875956 MOENS H and TURCK F. VNF-P: A model for efficient placement of virtualized network functions[C]. International Conference on Network and Service Management, Beijing, China, 2014: 418–423. doi: 10.1109/cnsm.2014.701. ZHANG Lijun, HERMANS H, and JANSEN D. Logic and model checking for Hidden Markov Models[C]. International Conference on Formal Techniques for Networked and Distributed Systems, Berlin, Germany, 2005: 98–112. doi: 10.1007/11562436_9. ZHANG Zengyin, YUAN Changan, HU Jianjun, et al. HMM training method based on GEP and Baum-Welch algorithms[J]. Computer Engineering & Design, 2010, 31(9): 2027–2029. XIONG Yan, CHEN Huanhuan, MIAO Fuyou, et al. A quantum genetic algorithm to solve combinatorial optimization problem[J]. Acta Electronica Sinica, 2004, 32(11): 1855–1858. BOULOUTAS A, HART G W, and SCHWARTZ M. Two extensions of the Viterbi algorithm[J]. IEEE Transactions on Information Theory, 2002, 37(2): 430–436. doi: 10.1109/18.75270 ZHANG Lifang and ZHANG Xiping. Network traffic prediction based on BP neural networks optimized by quantum genetic algorithm[J]. Computer Engineering & Science, 2016, 10(3): 12–20. ZHANG Ying, BEHESHTI N, BELIVEAU L, et al. StEERING: A software-defined networking for inline service chaining[C]. IEEE International Conference on Network Protocols, Raleigh, USA, 2014: 1–10. doi: 10.1109/icnp.2013.673. BASTA A, HOFFMANN K, HOFFMANN K, et al. Applying NFV and SDN to LTE mobile core gateways, the functions placement problem[C]. The Workshop on All Things Cellular: Operations, Chicago, USA, 2014: 33–38. doi: 10.1145/2627585.2627592. 刘彩霞, 卢干强, 汤红波, 等. 一种基于Viterbi算法的虚拟网络功能自适应部署方法[J]. 电子与信息学报, 2016, 38(11): 2922–2930. doi: 10.11999/JEIT1650507LIU Caixia, LU Ganqiang, TANG Hongbo, et al. Adaptive deployment method for virtualized network function based on Viterbi algorithm[J]. Journal of Electronics &Information Technology, 2016, 38(11): 2922–2930. doi: 10.11999/JEIT1650507 ZEGURA E, CALVERT K, and BHATTACHARJEE S. How to model an Internetwork[J]. Proceedings of IEEE Infocom, 1996, 2: 594–601. doi: 10.1109/infcom.1996.493353 ORLOWSKI S, WESSALY R, PIORO M, et al. SNDlib 1.0-survivable network design library[J]. Networks, 2010, 55(3): 276–286. doi: 10.1002/net.20371 CLAYMAN S, MAINI E, GALIS A, et al. The dynamic placement of virtual network functions[C]. Network Operations and Management Symposium, Seoul, Korea, 2014: 1–9. doi: 10.1109/noms.2014.6838412. SAHHAF S, TAVERNIER W, ROST M, et al. Network service chaining with optimized network function embedding supporting service decompositions[J]. Computer Networks the International Journal of Computer & Telecommunications Networking, 2015, 93(P3): 492–505. doi: 10.1016/j.comnet.2015.09.035 -





 下载:
下载:


 下载:
下载:
