Synthesis of Multi-constrained Sparse Rectangular Arrays
-
摘要:
针对多约束稀布矩形阵列天线的优化设计问题,该文提出一种新的矩阵映射(NMM)方法。首先,综合考虑阵元的可分布范围与可分布数量,重新定义阵元坐标矩阵的维数以提高阵元分布的自由度。其次,当坐标矩阵定义的阵元数量大于实际阵元数量时,建立选择矩阵以确定各阵元的取舍。再次,针对现有矩阵映射方法无法完全避免不可行解的问题,构建了一种NMM方法,通过两种不同的矩阵映射函数将多约束优化问题转换为无约束优化问题。最后进行仿真对比实验,实验结果证明了算法的有效性。
Abstract:A Novel Matrix Mapping (NMM) method is proposed for the synthesis of sparse rectangular arrays with multiple constraints. Firstly, the sizes of element coordinate matrices are resized to improve the Degree Of Freedom (DOF) of elements by taking account of both placeable number and distributable range of elements. Then, a selection matrix is established to determine which elements should be turned off when the coordinate matrices should be thinned. By establishing two different mapping functions, a NMM method is presented to overcome the drawbacks of existing methods in terms of flexibility and effectiveness. Finally, comparison experiments are conducted to verify the effectiveness of the proposed method. The numerical validation points out that the proposed method outperforms the existing methods in the design of sparse rectangular arrays.
-
Key words:
- Antenna arrays /
- Sparse planar arrays /
- Constrained optimization /
- Sidelobe level
-
表 1 实验1仿真结果对比(dB)
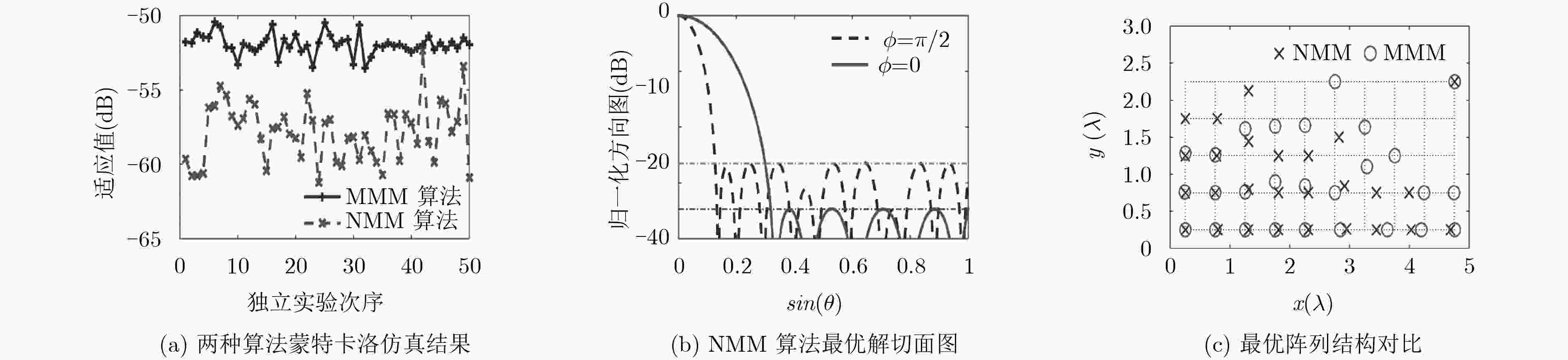
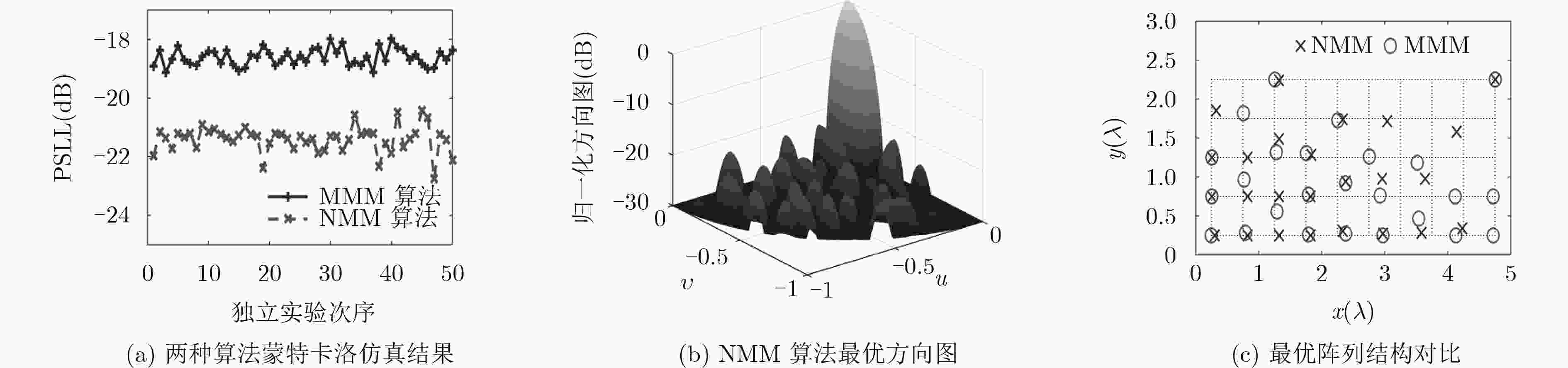
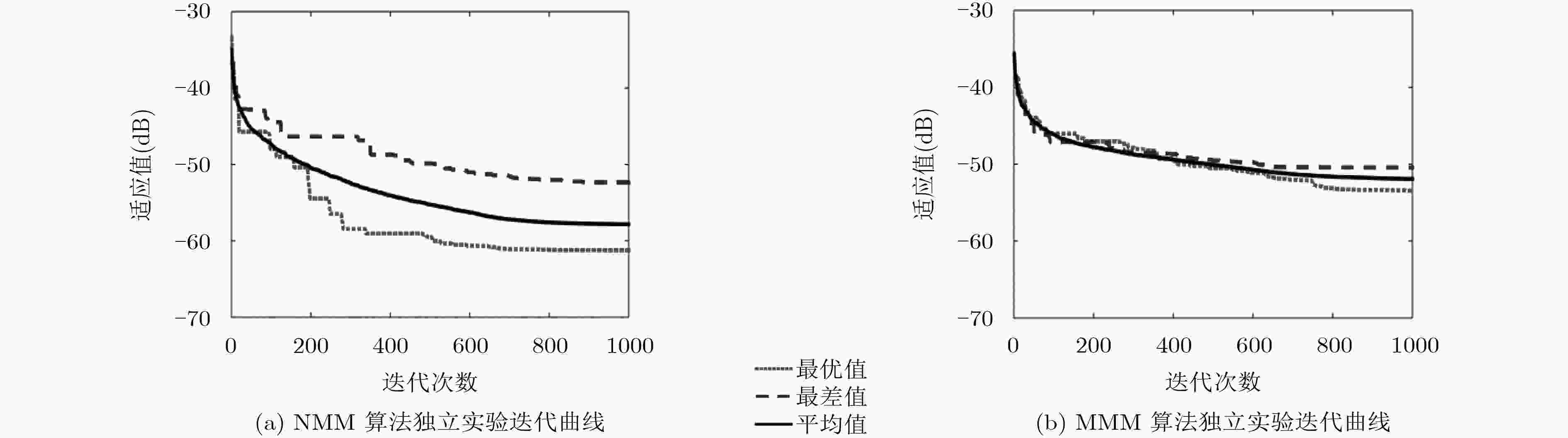
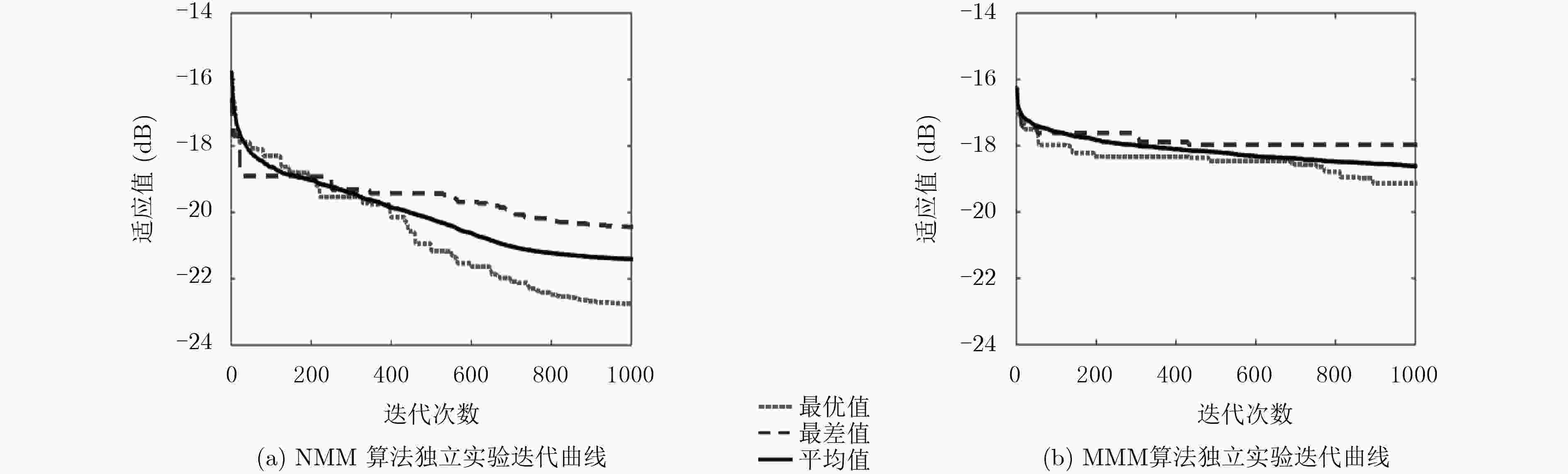
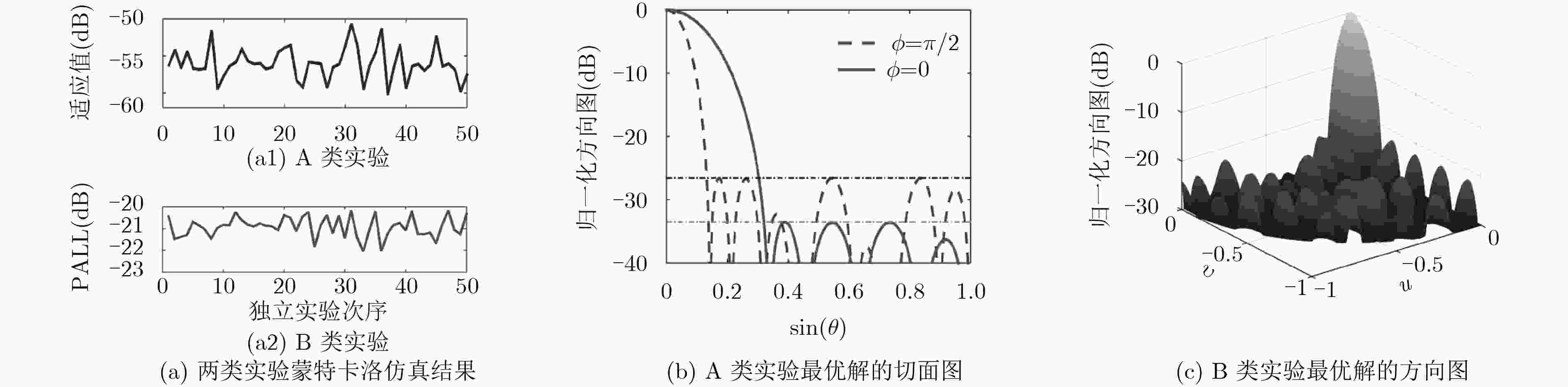
实验类型 方法 最优值 最差值 均值 方差 A NMM –61.2178 –52.3630 –57.8363 4.0813 MMM –53.5222 –50.4478 –51.9317 0.4940 B NMM –22.7591 –20.4355 –21.4060 0.1993 MMM –19.1338 –17.9751 –18.5972 0.0875 表 2 算法运算效率对比
实验1 方法 平均运行时间(s) 平均内存峰值使用量(kB) 平均适应值(dB) 可行解占比(%) A MMM算法 247.614 620 –51.9317 44 本文方法 283.704 620 –57.8363 100 B MMM算法 20472.744 904 –18.5972 60 本文方法 25823.421 984 –21.4060 100 表 3 实验2仿真结果对比(dB)
实验类型 方法 最优值 最差值 均值 方差 A NMM –60.2701 –50.6686 –56.0144 4.7592 B NMM –22.0422 –20.1613 –20.9181 0.2303 -
DARVISH A and EBRAHIMZADEH A. Improved fruit-fly optimization algorithm and its applications in antenna arrays synthesis[J]. IEEE Transactions on Antennas & Propagation, 2018, 66(4): 1756–1766. doi: 10.1109/TAP.2018.2800695 ZHANG Xuejing, HE Zishu, LIAO Bin, et al. Pattern synthesis for arbitrary arrays via weight vector orthogonal decomposition[J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1286–1299. doi: 10.1109/TSP.2017.2787143 ZHANG Xuejing, HE Zishu, LIAO Bin, et al. Pattern synthesis with multi-point accurate array response control[J]. IEEE Transactions on Antennas & Propagation, 2017, 65(8): 4075–4088. doi: 10.1109/TAP.2017.2718582 LI Xun, DUAN Baoyan, ZHOU Jinzhu, et al. Planar array synthesis for optimal microwave power transmission with multiple constraints[J]. IEEE Antennas & Wireless Propagation Letters, 2017, 16: 70–73. doi: 10.1109/LAWP.2016.2555980 LEEPER D. Isophoric arrays—Massively thinned phased arrays with well-controlled sidelobes[J]. IEEE Transactions on Antennas & Propagation, 1999, 47(12): 1825–1835. doi: 10.1109/8.817659 KEIZER W. Synthesis of thinned planar circular and square arrays using density tapering[J]. IEEE Transactions on Antennas & Propagation, 2014, 62(4): 1555–1563. doi: 10.1109/TAP.2013.2267194 李龙军, 王布宏, 夏春和. 基于改进迭代FFT算法的均匀线阵交错稀疏布阵方法[J]. 电子与信息学报, 2016, 38(4): 970–977. doi: 10.11999/JEIT150749LI Longjun, WANG Buhong, and XIA Chunhe. Interleaved thinned linear arrays based on modified iterative FFT technique[J]. Journal of Electronics &Information Technology, 2016, 38(4): 970–977. doi: 10.11999/JEIT150749 ZHANG Li, JIAO Yongchang, WENG Zibin, et al. Design of planar thinned arrays using a Boolean differential evolution algorithm[J]. IET Microwaves, Antennas & Propagation, 2010, 4(12): 2172–2178. doi: 10.1049/iet-map.2009.0630 DONELLI M, MARTINI A, and MASSA A. A hybrid approach based on PSO and Hadamard difference sets for the synthesis of square thinned arrays[J]. IEEE Transactions on Antennas & Propagation, 2009, 57(8): 2491–2495. doi: 10.1109/TAP.2009.2024570 YAN Fei, YANG Peng, YANG Feng, et al. Synthesis of planar sparse arrays by perturbed compressive sampling framework[J]. IET Microwaves Antennas & Propagation, 2016, 10(11): 1146–1153. doi: 10.1049/iet-map.2015.0775 VIANI F, OLIVERI G, and MASSA A. Compressive sensing pattern matching techniques for synthesizing planar sparse arrays[J]. IEEE Transactions on Antennas & Propagation, 2013, 61(9): 4577–4587. doi: 10.1109/TAP.2013.2267195 于波, 陈客松, 朱盼, 等. 稀布圆阵的降维优化方法[J]. 电子与信息学报, 2014, 36(2): 476–481. doi: 10.3724/SP.J.1146.2013.00526YU Bo, CHEN Kesong, Zhu Pan, et al. An optimum method of sparse concentric rings array based on dimensionality reduction[J]. Journal of Electronics &Information Technology, 2014, 36(2): 476–481. doi: 10.3724/SP.J.1146.2013.00526 CHEN Kesong, YUN Xiaohua, HE Zishu, et al. Synthesis of sparse planar arrays using modified real genetic algorithm[J]. IEEE Transactions on Antennas & Propagation, 2007, 55(4): 1067–1073. doi: 10.1109/TAP.2007.893375 LIU Heng, ZHAO Hongwei, LI Weimei, et al. Synthesis of sparse planar arrays using matrix mapping and differential evolution[J]. IEEE Antennas & Wireless Propagation Letters, 2016, 15: 1905–1908. doi: 10.1109/LAWP.2016.2542882 LIN Zhiqiang, JIA Weimin, YAO Minli, et al. Synthesis of sparse linear arrays using vector mapping and simultaneous perturbation stochastic approximation[J]. IEEE Antennas & Wireless Propagation Letters, 2012, 11: 220–223. doi: 10.1109/LAWP.2012.2188266 贾维敏, 林志强, 姚敏立, 等. 一种多约束稀布线阵的天线综合方法[J]. 电子学报, 2013, 41(5): 926–930. doi: 10.3969/j.issn.0372-2112.2013.05.015JIA Weimin, LIN Zhiqiang, YAO Minli, et al. A synthesis technique for linear sparse arrays with multiple constraints[J]. Acta Electronica Sinica, 2013, 41(5): 926–930. doi: 10.3969/j.issn.0372-2112.2013.05.015 DAI Dingcheng, YAO Minli, MA Hongguang, et al. An effective approach for the synthesis of uniformly excited large linear sparse array[J]. IEEE Antennas & Wireless Propagation Letters, 2018, 17(3): 377–380. doi: 10.1109/LAWP.2018.2790907 ZHANG Fenggan, JIA Weimin, and YAO Minli. Linear aperiodic array synthesis using differential evolution algorithm[J]. IEEE Antennas & Wireless Propagation Letters, 2013, 12(9): 797–800. doi: 10.1109/LAWP.2013.2270930 -





 下载:
下载:



 下载:
下载:
